偏心圓柱薄殼輸入功率流特性研究

張冠軍, 李天勻, 朱 翔

(華中科技大學 船舶與海洋工程學院， 武漢 430074)

圓柱殼結構在船舶與海洋工程、航空航天、石油開采及管道輸送等領域得到了廣泛的應用，如飛機機體和輸油管道等都是圓柱殼結構。國內外學者對圓柱殼結構的靜動態特性也進行了大量的研究。而偏心柱殼在實際工程中也有很大的應用空間，如偏心管道，另一方面，即使是針對原設計的圓柱殼結構，由于制造工藝、加工誤差等諸多因素的影響，也可能產生不可忽略的偏心率等偏差[1-3]。由于其截面的特殊性，想要獲得這類殼體的解析解或半解析解要比理想圓柱殼困難得多。這是因為圓柱殼的動力平衡方程可以化為一個常系數偏微分方程來進行求解，但偏心柱殼的動力平衡方程為一個變系數的偏微分方程，難以求解。因此關于偏心柱殼振動特性的相關研究目前還未廣泛展開。

Chang等[4]最早對偏心柱殼進行了靜力學分析，將偏心柱殼分為常厚度和變厚度部分，通過界面處位移及應力連續建立力學平衡方程，方程中存在大量的為滿足連續性條件而引入的系數，不便求解，文中也只給出了理論推導，并未計算實際算例。針對偏心柱殼以及周向變厚度殼體，后來研究者主要采用傳遞矩陣法、級數展開法和有限元法等進行求解。熊路等[5]將偏心柱殼沿周向微分，假設在每個微段內殼體厚度是均勻的，采用傳遞矩陣法結合指數矩陣精細積分法求解了偏心柱殼的固有頻率，文中只考慮了對稱模態。黃玉盈等[6]采用傳遞矩陣法研究了一端剛固的軸向變厚度圓柱蓄水池的自由振動特性。曹雷等[7]同樣采用傳遞矩陣法對軸向加肋變厚度圓柱殼體的自由振動特性進行了研究，但傳遞矩陣法受單元傳遞矩陣的計算精度、傳遞矩陣連乘過程中的累積誤差以及計算機的舍入(或截斷)誤差影響，狀態向量在傳遞過程中會產生一定的精度損失，對于指數矩陣還存在收斂穩定性問題，且計算效率較低。Hasheminejad等[8-9]通過級數展開假設殼體變量函數，對內外圓不同心的偏心中空圓柱體自由振動及聲輻射問題進行了研究，通過二分法求解殼體的振動方程；該方法主要針對壁厚較厚的偏心柱殼，但該方法最后的頻率方程過于繁雜，大量未知系數相互耦合，需要進行截斷，存在一定截斷誤差。Bacciocchi等[10]采用一種廣義積分法研究變厚度板殼的自由振動特性，該方法類似于有限元法對結構進行離散。Vidal等[11]則采用有限元法研究了中間帶有偏心孔的圓柱殼的自由振動特性，該方法建模工作量較大且不利于參數化分析。

本文根據偏心柱殼截面的幾何特性，將偏心柱殼轉化為周向變厚度柱殼。基于Flügge薄殼理論[12]推導出偏心柱殼的受迫振動方程，采用波傳播的思想將偏心柱殼位移以雙Fourier級數形式展開，周向變厚度表示為周向角度坐標的函數，通過三角函數變換將變系數的偏微分方程組轉換為周向模態階數相互耦合的有限階常系數線性方程組，通過求解得到偏心柱殼的受迫振動位移響應，進而計算偏心柱殼的輸入功率流，并研究了殼體相關參數對輸入功率流的影響。

1 研究對象

1.1 偏心柱殼截面的幾何形狀

偏心柱殼橫截面如圖1所示，A為外圓圓心，B為內圓圓心，r1為外圓半徑，r2為內圓半徑。O為AB中點，|AB|=e為偏心距。C為外圓上一點，OC交內圓于點D。

圖1 偏心柱殼橫截面示意圖

根據文獻[5]，偏心柱殼可視為以O為圓心，殼體平均半徑為R=(r1+r2)/2，厚度為h(θ)=h0-ecosθ的周向變厚度圓柱殼，h0=r1-r2，表示殼體平均厚度。

1.2 基本假設及坐標系

偏心柱殼幾何參數和坐標如圖2所示，殼體無限長，材料密度為ρ，楊氏模量為E，泊松比為μ，材料阻尼因子為η。坐標系選取圓柱坐標系(x,θ,r)，其中x為軸向坐標，θ為周向坐標，r為殼體徑向坐標，并設u,v,w分別表示殼體中面的軸向、周向和徑向位移。

圖2 偏心柱殼幾何參數和坐標

2 基本理論推導

2.1 殼體中的位移及內力基本關系

根據Flügge薄殼理論，殼體的幾何方程為

(1)

式中:εx和εθ為殼體中面內各點的線應變;γxθ為剪應變；κx，κθ和τ代表了中面內各點主曲率及扭率的改變。

殼體物理方程為

(2)

式中；Nx,Nθ分別為x和θ方向單位寬度上的面內力；Nθx和Nxθ為平面內單位寬度上的剪切力；Mx,Mθ和Mxθ,Mθx分別為單位寬度上的彎矩和扭矩。K和D分別表示殼體微元的拉壓剛度和彎曲剛度，表達式為

(3)

殼體內的動力平衡方程為

(4)

式中:Qx和Qθ分別為x和θ方向單位寬度上的橫剪力；F為殼體法向受到的外力，外法線方向為正。

將方程組(4)中第4式和第5式代入到第2式和第3式并聯立第1式，可得到新的平衡方程

(5)

為便于推導，引入如下無量綱參數

(6)

φ記為偏心柱殼的偏心率，表示殼體偏心距與平均厚度的比值，用來衡量殼體的偏心程度。

此時有：

h=h0(1-φcosθ)

(7)

此時式(3)中殼體的拉壓剛度K和彎曲剛度D均是與周向坐標θ有關的函數，設：

(8)

將式(7)代入式(8)中有：

K=K0(1-φcosθ)，D=D0(1-φcosθ)3

(9)

將式(1)，(2)，(9)代入式(5)中，可得到矩陣形式表達的平衡方程

(10)

其中各算子Lij(i,j=1,2,3)表達式如下：

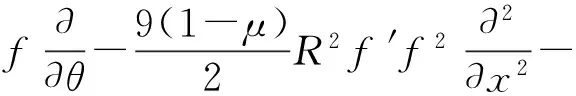
L33=(f+Hf3+6Hf2f′+3Hf2f′2)w+

2.2 偏心柱殼的位移展開形式及外力表達式

參考圖1可知，偏心柱殼僅有一條對稱軸，即圖中x軸，存在對稱和反對稱位移模式。對于對稱位移模式，可以將殼體位移在軸向和周向展開成雙Fourier級數形式

(11)

對于反對稱位移模式，其展開形式為

(12)

式中:l是軸向波數解的序號;kl為殼體的軸向波數；Ul,n，Vl,n，Wl,n分別為對應于周向模態階數n的殼體軸向、周向和徑向位移的Fourier幅值系數。

設柱殼在點(x0,θ0)處受到簡諧點激勵載荷

F(x,θ,t)=F0δ(θ)δ(x)exp(iωt)

(13)

式中：F0表示作用在(x0,θ0)處的集中力幅值。當在殼體上作用多個集中點激勵力時，將上式中的θ改寫為θj(j=0,1,2,...)。

上式中，令x=0，θ=θ0得：

F(x,θ,t)=F0δ(θ0)δ(0)exp(iωt)

(14)

對于對稱位移模式，將其展開成周向模態階數疊加的形式：

(15)

聯立式(14)和式(15)可得：

F0δ(θ0)δ(0)exp(iωt)=

(16)

對上式進行正交化處理可得：

(17)

對于反對稱位移模式：

(18)

2.3 偏心柱殼的受迫振動方程

將式(11)或式(12)及式(15)代入式(10)，并通過三角函數變換，可以得到三個關于Ul,n，Vl,n，Wl,n相互耦合的新方程

(19)

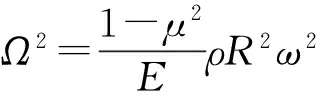
式(19)中的位移幅值Ul,n，Vl,n，Wl,n關于不同周向模態階數n相互耦合成無窮多個線性方程，需對方程組進行截斷求解，即對n進行截斷選取。

當n取有限項p時，可以得到3p個線形方程，并寫成矩陣形式：

=F

(20)

M為3p階方陣，由式(19)中的系數循環迭代而成。

則由式(20)可得：

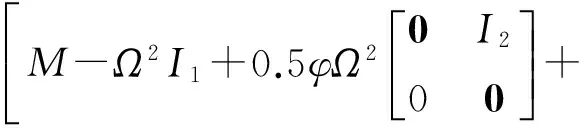
(21)

則殼體位移幅值系數Ul,n，Vl,n，Wl,n可由式(21)得到。

2.4 殼體輸入功率流

根據振動功率流的定義，因外激勵力呈簡諧變化，故位移響應和速度響應均呈簡諧變化，設：

(22)

(23)

則：

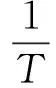
(24)

因此，可以求得外力輸入到結構的功率為

(25)

為便于比較，將輸入功率流無量綱化為

(26)

將輸入功率流進行級運算可得

(27)

式中:W0=1×10-12W。

3 數值計算及分析

3.1 算法收斂性及可靠性驗證

對偏心柱殼輸入功率流分析時周向模態階數n的截斷選取進行收斂性分析，由式(21)得到殼體振動位移，進而計算殼體的輸入功率流。本文計算中采用文獻[13]所提出的加阻尼數值積分法考慮材料阻尼因子的影響。驗證模型參數：殼體無限長，材料密度為ρ=7 800 kg/m3，楊氏模量為E=2.1×1011Pa，泊松比為μ=0.3，殼體平均厚度h0=0.02 m，中面半徑R=1 m，點激勵力幅值F0=1 N，無量綱頻率Ω=3，阻尼因子取η=0.01。

從圖3可以看出，當偏心率φ較小時，偏心柱殼輸入功率流收斂所需的截斷項數p相對較少，當偏心率φ較大，尤其偏心率φ=0.7時需取更高的截斷項數以保證結果收斂。隨著截斷項數的增加，計算結果的收斂精度會更高，但過多的截斷項數會導致計算效率的降低。從圖中可以看出，在截斷項數p=60，偏心柱殼輸入功率流趨于穩定，本文計算中取截斷項數p=70。

圖3 輸入功率流隨周向模態階數的收斂性曲線

為了驗證本文偏心柱殼振動理論模型及計算方法的可靠性，令偏心率φ=0，將偏心柱殼退化為圓柱殼，并將本文方法計算退化模型的輸入功率流與已有文獻[13]進行對比，模型參數按文獻選取，結果如圖4(a)所示。同時選取有限長偏心柱殼與FEM結果進行了對比，結果如圖4(b)所示，(偏心柱殼長度L=50 m，殼體厚度h0=0.02 m，偏心率φ=0.5，其它參數如文獻[13]；對于偏心柱殼有限元模型，為滿足每個振動彎曲波波長內至少6個單元，則單元尺寸約為0.08 m，單元數量為50 000個)。

(a)

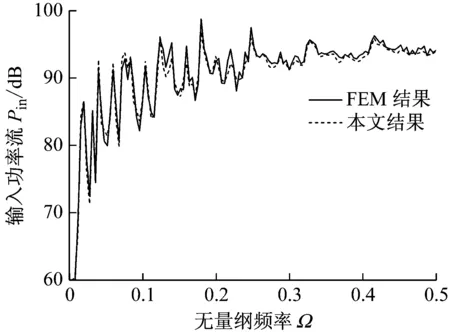
(b)

由圖4可見本文方法計算結果與文獻及FEM計算結果吻合很好，表明本文所建立的偏心柱殼振動理論模型及計算方法準確可靠。

3.2 激勵力位置對殼體輸入功率流的影響

對于偏心柱殼，截面各處的殼體厚度沿周向是變化的，激勵力施加在殼體截面不同位置將對殼體的振動產生影響。本節研究了激勵力分別施加在θ=0,π/2,π對殼體輸入功率流的影響，激勵力位置如圖5所示，不同激勵力下的輸入功率流如圖6所示。

圖5 不同激勵力位置

(a)

(b)

從圖6可以看出，激勵力施加在不同位置對偏心柱殼的輸入功率流有明顯的影響，激勵力施加在θ=0的位置殼體輸入功率流相對較大，施加在θ=π的位置輸入功率流相對較小，主要由于在θ=0的位置，殼體截面厚度較小，相對剛度也較小，使得偏心柱殼的輸入功率流增大，而在θ=π的位置，殼體截面厚度較大，相對剛度也較大，則輸入功率流較小。

3.3 偏心率對殼體輸入功率流的影響

對于偏心柱殼，偏心率大小不同，對偏心柱殼的結構剛度、振動特性等影響也不相同，本節研究了偏心率對偏心柱殼輸入功率流的影響，同時也與圓柱殼(即偏心率φ=0)作了對比，激勵力施加在θ=0處。圖7給出了不同偏心率下偏心柱殼的輸入功率流隨頻率的變化。

(a)

(b)

由圖7可以看出，當激勵力施加在θ=0位置時，不同偏心率下偏心柱殼的輸入功率流曲線在總體趨勢上是一致的：即隨頻率的增大不斷出現峰值，整體趨勢呈現先增大后趨于穩定。但偏心率對偏心柱殼的輸入功率流幅值及對應的頻率點也有明顯影響：隨著偏心率的增大，殼體的輸入功率流也增大，圓柱殼的輸入功率流最小，主要是因為偏心率的存在使其模態剛度降低，同時殼體輸入功率流峰值向低頻偏移。對于圓柱殼，在殼體環頻率(對應于無量綱頻率Ω=1)處殼體輸入功率流最大，對于偏心柱殼，隨著偏心率的增大，殼體輸入功率流的最大值不斷向低頻移動。

3.4 殼厚比對結構輸入功率流的影響

本節研究了不同殼厚比h0/R對偏心柱殼輸入功率流的影響。圖8給出了不同殼厚比偏心柱殼的輸入功率流隨頻率的變化曲線。

(a)

(b)

由圖8可以看出，殼厚比的改變對偏心柱殼的輸入功率流也有較大影響，當殼厚比減小時，結構的輸入功率流增大，峰值對應的頻率向低頻偏移，說明殼厚比減小，偏心柱殼剛度降低，抗振能力下降。殼厚比的改變對偏心柱殼輸入功率流最大值所對應的頻率沒有明顯影響。

3.5 材料阻尼因子對結構輸入功率流的影響

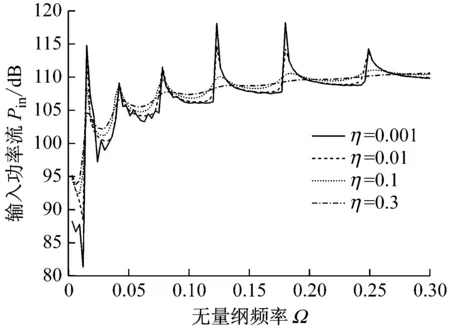
本節研究了不同材料阻尼因子η對偏心柱殼輸入功率流的影響。圖9給出了不同材料阻尼因子偏心柱殼的輸入功率流隨頻率的變化曲線。

由圖9可以看出，材料阻尼因子主要影響偏心柱殼共振頻率處的輸入功率流，隨著阻尼因子的增大，偏心柱殼共振頻率處的輸入功率流峰值降低，輸入功率流曲線趨于平順，表明材料阻尼因子能有效降低結構的共振響應，但對非共振頻域影響較小。

4 結 論

本文基于Flügge薄殼理論推導出偏心柱殼的受迫振動方程，采用波傳播的思想將殼體位移以雙Fourier級數形式展開，周向變厚度表示為周向角度坐標的函數，通過三角函數變換將變系數的偏微分方程組轉換為周向模態階數相互耦合的有限階常系數線性方程組，通過求解得到偏心柱殼受迫振動下的位移響應，進而計算偏心柱殼的輸入功率流，得到如下結論：

(a)

(b)

(1) 通過與文獻及FEM結果進行對比，驗證了本文所建立的偏心柱殼振動理論模型及計算方法的準確性。

(2) 激勵力施加在θ=0的位置，偏心柱殼的輸入功率流相對較大；施加在θ=π的位置，輸入功率流相對較小。

(3) 偏心柱殼的輸入功率流隨偏心率的增大不斷出現峰值，且隨偏心率的增大峰值向低頻偏移，整體趨勢線逐漸增大后趨于平穩。激勵點在0°位置，偏心率越大則殼體的輸入功率流也越大，圓柱殼的輸入功率流最小。

(4) 當殼厚比減小時，殼體的輸入功率流不斷增大，峰值對應的頻率向低頻偏移。

(5) 材料阻尼因子能有效降低偏心柱殼共振頻率處的輸入功率流峰值，但對非共振頻域影響較小。

[1] 龔有根, 賀玲鳳. 含有初始凹陷缺陷圓柱殼穩定承載能力的實驗研究與數值計算[J]. 實驗力學, 2010, 25(1): 73-80.

GONG Yougen, HE Lingfeng. Experimental study and numerical calculation of stability and load-carrying capacity of cylindrical shell with initial dent[J]. Journal of Experimental Mechanics, 2010, 25(1): 73-80.

[2] 張盛, 金翔, 周樺. 加肋圓柱殼制造誤差對聲學性能的影響研究[J]. 中國艦船研究, 2011, 6(4): 43-50.

ZHANG Sheng, JIN Xiang, ZHOU Hua. Influence of construction error on sound radiation for ring-stiffened cylindrical shell[J]. Chinese Journal of Ship Research, 2011, 6(4): 43-50.

[3] 王日清, 董楓. 高精度偏心套的加工及檢測[J]. 科技情報開發與經濟, 2004, 14(9): 212-214.

WANG Riqing, DONG Feng. Processing and measuring of the eccentric adjusting sleeve with high-precision[J]. Sci/Tech Information Development and Economy, 2004, 14(9): 212-214.

[4] CHANG M, CHANG L L. Analysis of the eccentric cylindrical thin shell[J]. Applied Mathematics and Mechanics, 1994, 15(9): 887-895.

[5] 熊路, 李天勻, 朱翔, 等. 單層偏心圓柱薄殼的自由振動特性分析研究[J]. 固體力學學報, 2014, 35(6): 566-573.

XIONG Lu, LI Tianyun, ZHU Xiang, et al. The free vibration analysis of single layer eccentric cylindrical thin shells[J]. Chinese Journal of Solid Mechanics, 2014, 35(6): 566-573.

[6] 黃玉盈, 向宇. 變厚度圓柱蓄水池動力分析的傳遞矩陣法[J]. 振動工程學報, 1989(4): 23-32.

HUANG Yuying, XIANG Yu. Transfer matrix method on dynamic analysis of circular cylindrical tanks with variable wall-thickness[J]. Journal of Vibration Engineering, 1989(4): 23-32.

[7] 曹雷, 馬運義, 黃玉盈. 環肋加強變厚度圓柱殼的自由振動[J]. 華中科技大學學報: 城市科學版, 2007, 24(2): 63-66.

CAO Lei, MA Yunyi, HUANG Yuying. Free vibration of ring-stiffened circular cylindrical chell with variable thickness[J]. Journal of Huazhong University of Science and Technology(Urban Science Edition), 2007, 24(2): 63-66.

[8] HASHEMINEJAD S M, MOUSAVI-AKBARZADEH H. Three dimensional non-axisymmetric transient acoustic radiation from an eccentric hollow cylinder[J]. Wave Motion, 2013, 50(4): 723-738.

[9] HASHEMINEJAD S M, GHAHERI A. Free vibration analysis of elastic elliptic cylinders with an eccentric elliptic cavity[J]. International Journal of Mechanical Sciences, 2016, 108: 144-156.

[10] BACCIOCCHI M, EISENBERGER M, FANTUZZI N, et al. Vibration analysis of variable thickness plates and shells by the generalized differential quadrature method[J]. Composite Structures, 2016,156(1):218-237.

[11] VIDAL P, GALLEGO E, GUAITA M, et al. Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper[J]. Journal of Constructional Steel Research, 2008, 64(4): 480-492.

[12] FLüGGE W. Stress in shells[M]. Berlin: Springer-Verlag, 1973: 204-222.

[13] 徐慕冰. 圓柱殼-流場耦合系統的振動波傳播與能量流研究[D]. 武漢: 華中科技大學,1999.