具有內阻的旋轉復合材料軸的非線性自由振動與穩定性

任勇生， 張玉環， 時玉艷

(山東科技大學 機械電子工程學院，山東 青島 266590)

纖維復合材料由于比強度和比剛度高、抗疲勞和減振性能好，在包括能源、航空和汽車在內的許多工業技術領域內的結構設計中已經顯示出廣闊的應用前景。輕質纖維復合材料取代傳統的金屬材料用于直升機尾傳動軸以及汽車傳動軸的結構設計，不僅可以大大地降低重量，同時還能夠減少噪聲、提高傳動系統的抗振性能。然而，由于復合材料相比金屬材料具有更強的阻尼耗散能力，在超臨界旋轉狀態下，復合材料軸轉子系統受到內阻的影響，更容易產生失穩問題，由此引發的大振幅振動，往往會導致嚴重的后果。因此，為了精確地預測和優化旋轉復合材料軸的動力學特性，有必要綜合考慮非線性和材料阻尼的影響。由于針對轉子系統非線性振動現象的分析要比線性分析困難得多，所以，考慮內阻的旋轉復合材料非線性動力學建模與分析，是轉子動力學領域內具有挑戰性的研究工作。

Ishida等[1-3]研究具有四次非線性恢復力的旋轉軸非線性受迫振動以及對稱非線性旋轉軸內共振和非穩態振動。Cveticanin等[4]采用Galerkin法研究具有幾何和彈性非線性的轉子系統振動。Hosseini等[5]采用多尺度法研究具有曲率和慣性非線性的旋轉軸的自由振動。Rizwan等[6]研究具有彎曲大變形旋轉軸-剛盤不平衡轉子系統非線性受迫振動。Shahgholi等[7]研究簡支不對稱旋轉軸主共振和參數共振，非線性來自軸向可伸縮和大位移幅值。Khadem等[8]研究大振幅不可伸長的旋轉軸組合共振。然而，在上述文獻中均未考慮內阻對非線性振動的影響。

復合材料軸的內阻來源于材料內部的能量耗散。Saravanos等[9]提出了一個預測各向異性復合材料空心梁模態阻尼的有限元模型，但它僅適用于非旋轉的復合材料梁或者葉片。Sino等[10]基于簡化的均勻梁有限元模型(SHBT)，研究帶有剛盤和彈性支承的旋轉復合材料軸的動力學特性，其中采用黏彈性復合材料本構關系描述內阻特性。Ren等[11]基于變分漸進法(variational asymptotical approach)建立復合材料薄壁軸轉子系統的動力學模型，其中，采用單層-截面-軸多尺度方法對復合材料內阻進行建模。然而，上述研究由于均未考慮非線性因素的影響，僅適合于對旋轉復合材料軸進行線性振動分析。

一些涉及材料內阻對轉子非線性動力學響應影響的報道主要有：Shaw等[12]和Luczko[13]研究內阻對各向同性黏彈性平衡轉軸穩定性與自激振動分叉特性的影響；Shaw等[14]、陳予恕等[15]研究超臨界不平衡轉軸的非線性剛度和材料內阻對動力學響應行為的影響；曹樹謙[16]研究油膜和內阻共同影響下的不平衡非線性轉動軸的失穩規律。Ishida等[17]研究具有非線性恢復力和內阻的旋轉軸的受迫振動，發現在轉速超過第一階臨界速度的很寬的范圍內，都會產生自激振動。Hosseini[18]研究簡支旋轉軸的穩定性和分叉，阻尼耗散來源于粘彈性材料內阻和支承外阻，借助于中心流定理和規范型方法描述了旋轉軸在分叉點附近的動力學特性。近來，任勇生等[19-20]提出一個考慮Von Kármán幾何非線性和內阻的影響的旋轉復合材料薄壁軸的不平衡彎曲振動模型，并且分別采用數值積分和多尺度法研究了旋轉軸的非線性時間響應和主共振。但是，上述研究所采用的轉子系統模型或者是基于各向同性分布參數轉子的簡化模型，或者是基于集中參數模型，尚未見到同時涉及復合材料內阻建模及其影響的各向異性旋轉復合材料軸的耦合非線性動力學行為的研究報道。

本文提出一個考慮復合材料內阻的旋轉非線性復合材料軸的動力學模型，研究復合材料旋轉軸的內阻失穩和后臨界動力學特性。復合材料軸被簡化為一個具有大振幅的不可伸長的旋轉復合材料空心梁，它包括非線性曲率和慣性的影響。內阻來源于復合材料的粘彈性耗散特性。從基本的復合材料應力-應變本構關系和應變-位移關系出發，在導出復合材料軸的應變能、動能和阻尼耗散能的基礎上，采用擴展的Hamilton原理建立運動微分方程。建模過程對復合材料軸的壁厚(薄壁或厚壁)不做任何假設。為了預測旋轉復合材料軸的穩定邊界，首先采用復數坐標表示并借助于Galerkin法，對線性化彎曲振動方程進行求解，導出旋轉復合材料軸的復特征方程，進而得到臨界轉速和失穩閾。研究了纖維鋪層角、鋪層方式和長徑比的影響。為了研究旋轉復合材料軸的后臨界非線性行為和穩定性，采用Galerkin法對彎曲振動非線性偏微分方程組進行離散化，采用四階Runge-Kutta法進行數值積分,獲得位移時間響應圖、相平面圖和功率譜圖,研究不同參數對旋轉復合材料軸非線性動力學行為的影響。

1 運動方程

圖1表示長度為L的旋轉復合材料軸，軸的兩端簡支，直角坐標系(X,Y,Z)為慣性坐標系；(X0,Y0,Z0)為旋轉坐標系，(x,y,z)為局部坐標系，慣性坐標軸與軸的橫截面的主軸一致，坐標原點位于變形軸的中心線上的x點處。變形軸上x點沿X，Y和Z方向的位移分別為u(x,t)，v(x,t)和w(x,t)，扭轉角為φ(x,t)。假定復合材料軸繞X以定常角速度Ω旋轉；復合材料軸為細長的，因此剪切變形可以忽略不計；支承O是固定的，而支承O′沿X方向不受約束，所以復合材料軸沿其中心線的軸向是不可伸長的；此外，不考慮支承外阻尼的影響，復合材料的黏彈性耗散阻尼特性是系統中唯一的耗散來源。

圖1 旋轉復合材料軸結構示意圖

旋轉復合材料軸的動能表示如下[21]

(1)

式中:ω1，ω2和ω3分別表示坐標系(x,y,z)相對于(X,Y,Z)的轉動角速度；其中，“·”表示對時間t求偏導，m和I分別表示單位長度的質量和截面慣性矩，分別為

(2)

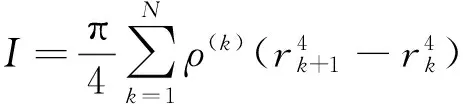
(3)

式中:N表示復合材料的層數;ρ(k)是第k層的密度;rk和rk+1分別是第k層的內徑和外徑。

旋轉復合材料軸的彈性勢能為

(4)

其中，在柱坐標下的微體積元dV=rdrdαdx，r和α分別表示極角和極徑。

柱坐標下表示的應力-應變方程為

(5)

(6)

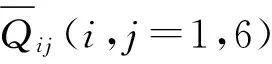
柱坐標下的應變-位移方程為

εx=e+ρ2rsinα-ρ3rcosα

(7)

γxα=rρ1

(8)

式中:ρi(i=1,2,3)表示軸的曲率。

沿軸的中心線的應變e可以表示為

(9)

式中:“′”表示對x求偏導。

軸的曲率ρi和ωi(i=1,2,3)分別表示為[22]

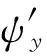
(10)

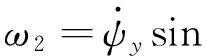
(11)

式中:ψ=φ+Ωt,ψy和ψz分別表示軸的橫截面繞z和y軸的轉角;φ表示橫截面繞x軸的扭轉角。

ψz和ψy可分別表示如下

(12)

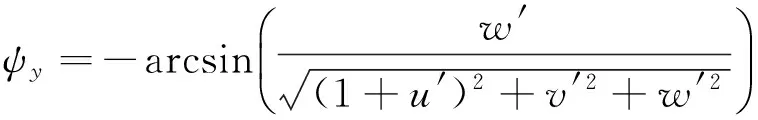
(13)

彈性勢能的變分

(14)

將式(5)和(7)代入式(14)，可得

(15)

其中

(16)

由于旋轉復合材料軸的支承O′在x軸方向是可運動的，所以，沿軸向不可伸長假設成立，即應變e=0，由此可得

(17)

與此同時，式(15)簡化為

(18)

如果假設橫向位移v和w是一階無窮小量，則軸向位移u為二階無窮小量。將式(12)和(13)代入曲率方程式(10)，展成泰勒級數，并只保留前三階無窮小量，得

(19)

同理，將式(12)和(13)代入角速度方程式(11)，近似得

(20)

旋轉復合材料軸阻尼耗散力的虛功

(21)

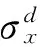
簡諧穩態運動下的黏彈性復合材料滿足下列本構方程

(22)

(23)

經過與式(18)類似的推導，可得

(24)

其中

(25)

D66(φ?w′+2φ″w″+φ′w?+4w′v?w″+

w′2v(4)+2w″2v″+2w′v″w?)-

D11(4v″v′v?+w(4)w′v′+w′v″w?+

3w″v′w?+w″2v″+v″3+v(4)v′2+v(4))-

(26)

D66(φ″v″+φ′v?+w″v″2+2w′v″v?)-

D11(4w″w′w?+v(4)v′w′+v′w″v?+

3v″w′v?+v″2w″+w″3+w(4)w′2+w(4))-

(27)

(28)

值得強調的是，式(26)，(27)和(28)是在旋轉坐標系下得到的，并且，為了著重研究非線性慣性和非線性剛度的影響，上述方程中只保留了內阻的線性項。

圓形截面軸的扭轉基礎頻率比彎曲頻率大得多，扭轉慣性項可以略去不計，此外，由于軸是細長的，轉動慣量很小，所以與轉動慣量相乘的非線性項也可忽略不計，據此，從上述方程中略去扭轉慣性項以及非線性扭轉剛度和慣性項，得彎-彎耦合非線性振動方程

D11(4v″v′v?+w(4)w′v′+w′v″w?+3w″v′w?+

w″2v″+v″3+v(4)v′2+v(4))=0

(29)

D11(4w″w′w?+v(4)v′w′+v′w″v?+

3v″w′v?+v″2w″+w″3+w(4)w′2+w(4))=0

(30)

或者

D11(4v″v′v?+w(4)w′v′+w′v″w?+3w″v′w?+

w″2v″+v″3+v(4)v′2+v(4))=0

(31)

D11(4w″w′w?+v(4)v′w′+v′w″v?+3v″w′v?+

v″2w″+w″3+w(4)w′2+w(4))=0

(32)

令

(33)

則有下列無量綱形式的運動方程

3w″v′w?+w″2v″+v″3+v(4)v′2+v(4)+

(34)

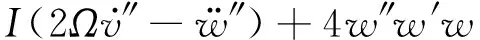
3v″w′v?+v″2w″+w″3+w(4)w′2+w(4)+

(35)

注：為簡單起見，式(34)、(35)變量字母上的橫杠均已去掉。

2 臨界轉速和失穩閾

(36)

設式(36)滿足簡支邊界條件的解，具有形式

U=eiλnsinnπx

(37)

其中，λn=ωn+idn(n=1,2，…)為復特征值，實部ωn和虛部dn分別為固有圓頻率和模態阻尼。顯然，如果虛部dn大于0，則轉子系統是穩定的，否則系統是不穩定的。

將式(37)代入式(36)，采用Galerkin法進行化簡，得下列復特征方程

(38)

將λn的表達式代入式(38)，分離實部和虛部，則可導出下列方程

n2π2(2IωnΩ-n2π2γdn)-n4π4=0

(39)

2(1+n2π2I)ωndn-

n2π2(2IΩdn+n2π2γωn)+n4π4γΩ=0

(40)

為了求臨界速度Ωcr，在式(39)和式(40)中令ωn=Ω=Ωcr，則有

(41)

2(1+n2π2I)Ωcrdn-

n2π2(2IΩdn+n2π2γΩcr)+n4π4γΩcr=0

(42)

由式(42)，得dn=0，代入式(41)，得

(43)

為了求失穩閾Ωinst.，分別在式(39)和(40)中令dn=0，同時令Ω=Ωinst.，得

(44)

ωn=Ωinst.

(45)

將式(45)代入式(44)，得

(46)

上述結果表明，Ωcr=Ωinst.，即臨界轉速等于失穩閾。由于本文模型并不包括外阻尼，所以，上述結論顯然是成立的。這說明，旋轉復合材料軸在超臨界狀態下會產生內阻失穩。

為了研究復合材料軸的鋪層角和長徑比對臨界轉速以及失穩閾的影響，數值算例取復合材料軸的平均半徑為0.176 m，厚度0.010 16 m，采用角鋪設[±θ]8的鋪層方式，長度L根據長徑比確定。復合材料力學參數如表1所示。

表1 材料力學特性

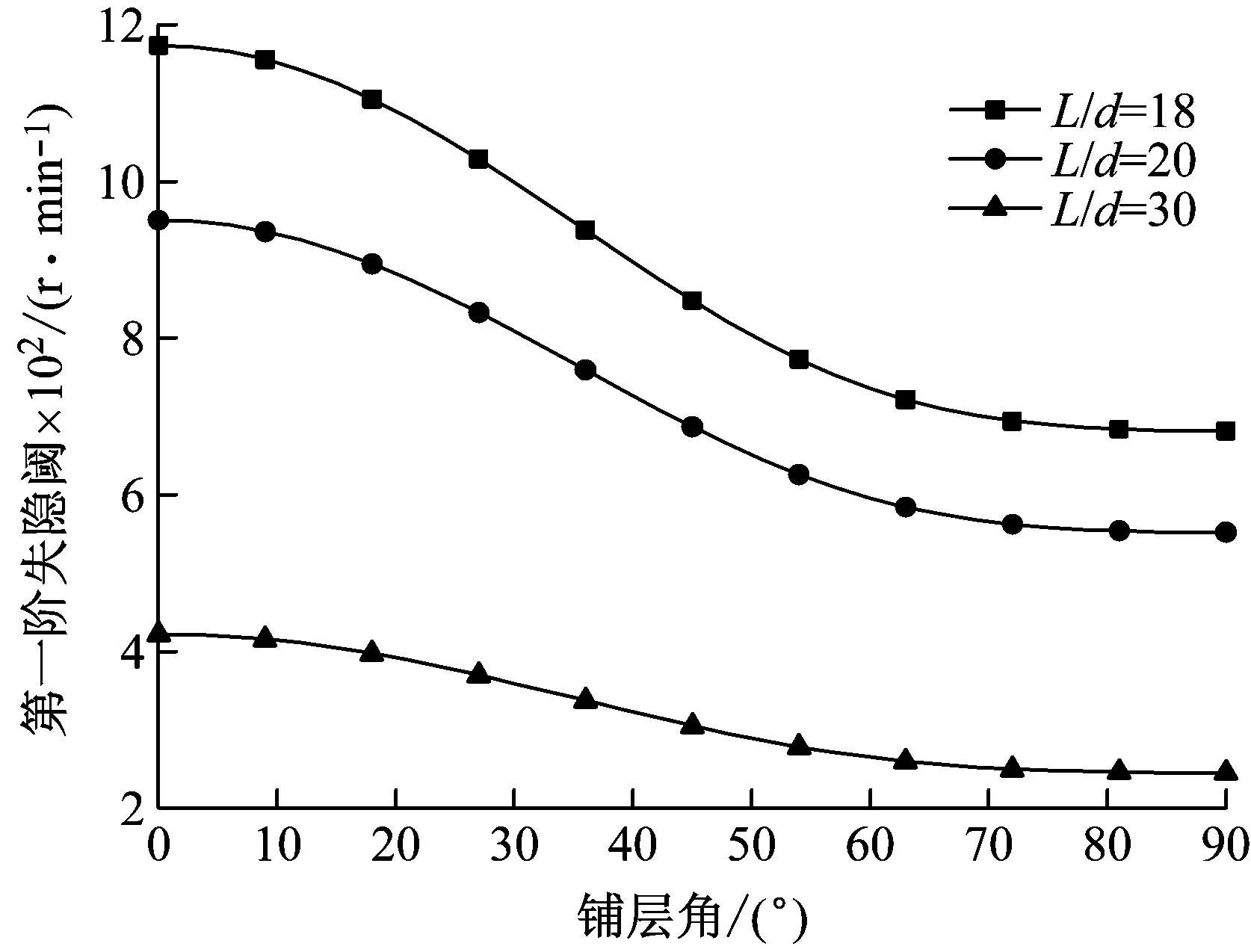
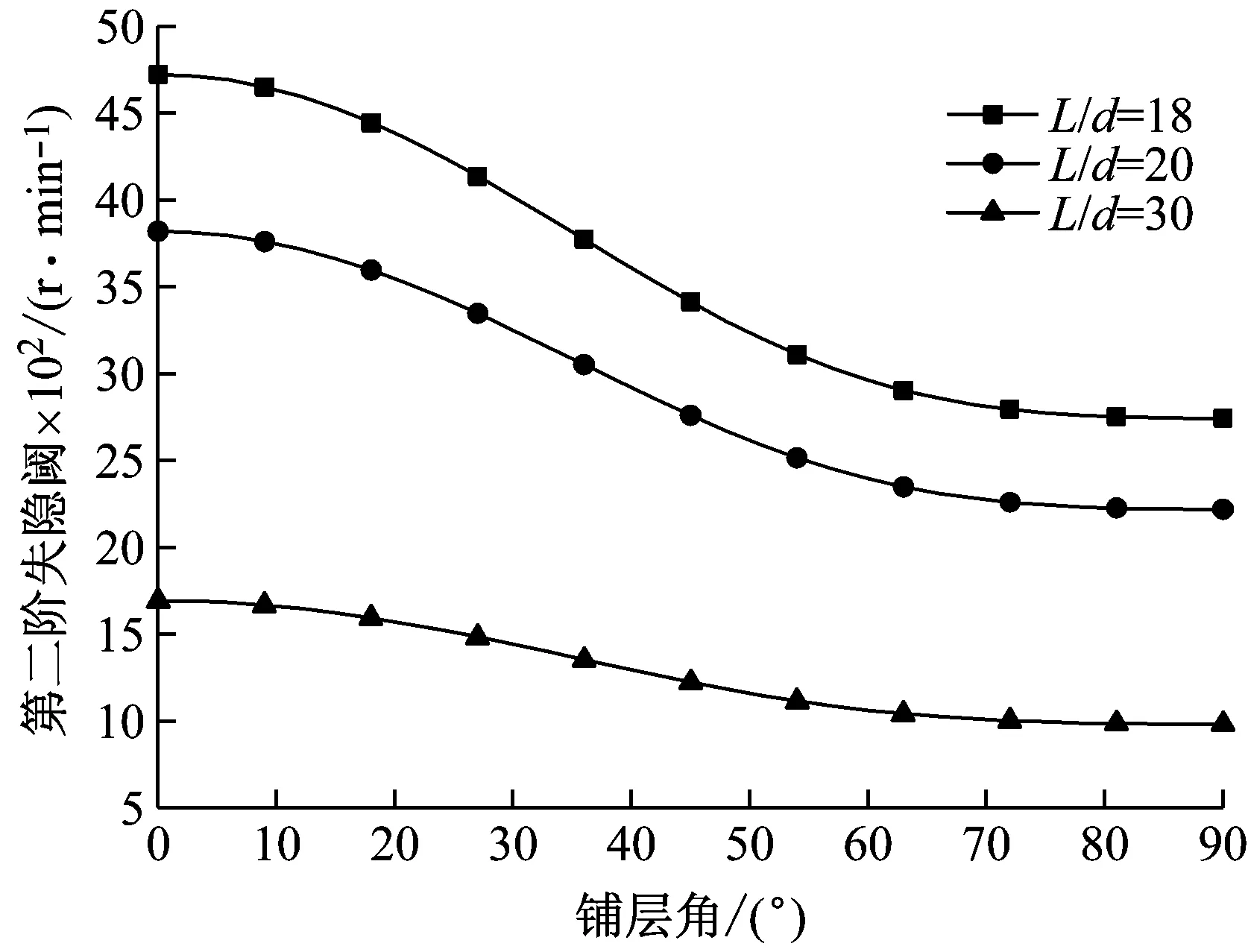
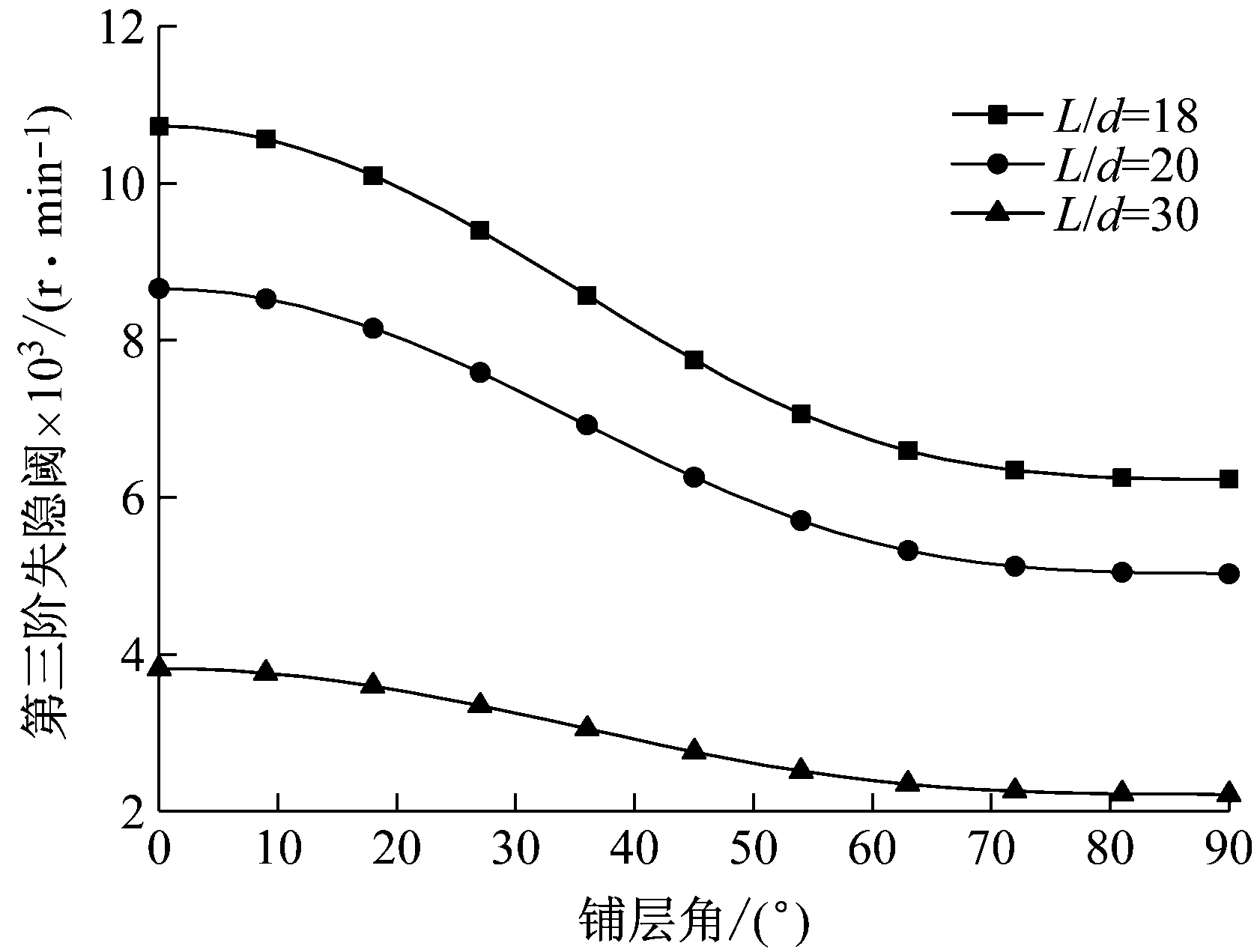
圖2表示旋轉復合材料軸的前三階失穩閾隨鋪層角的變化曲線，同時也給出三種不同的長徑比的影響。結果表明，失穩閾隨著鋪層角的增加而減小，這是因為纖維縱向的阻尼能力要低于其橫向的阻尼能力(見表1)，所以，纖維越靠近軸的縱向鋪設，沿此方向上的內阻能力也越弱，因此，導致旋轉軸產生失穩的轉速也就越大，即轉子系統越不容易發生失穩。圖2也表明，失穩閾隨著長徑比的增加而減小，說明在其它條件相同的情況下，長度較長的軸相對更容易失穩。這與文獻[10]的結論是一致的。

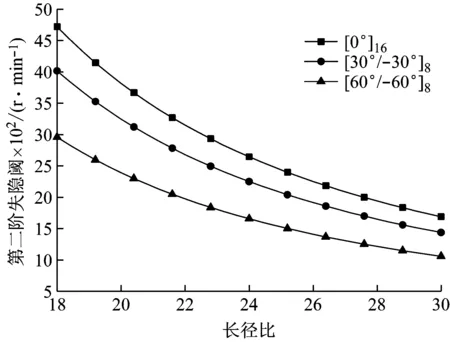
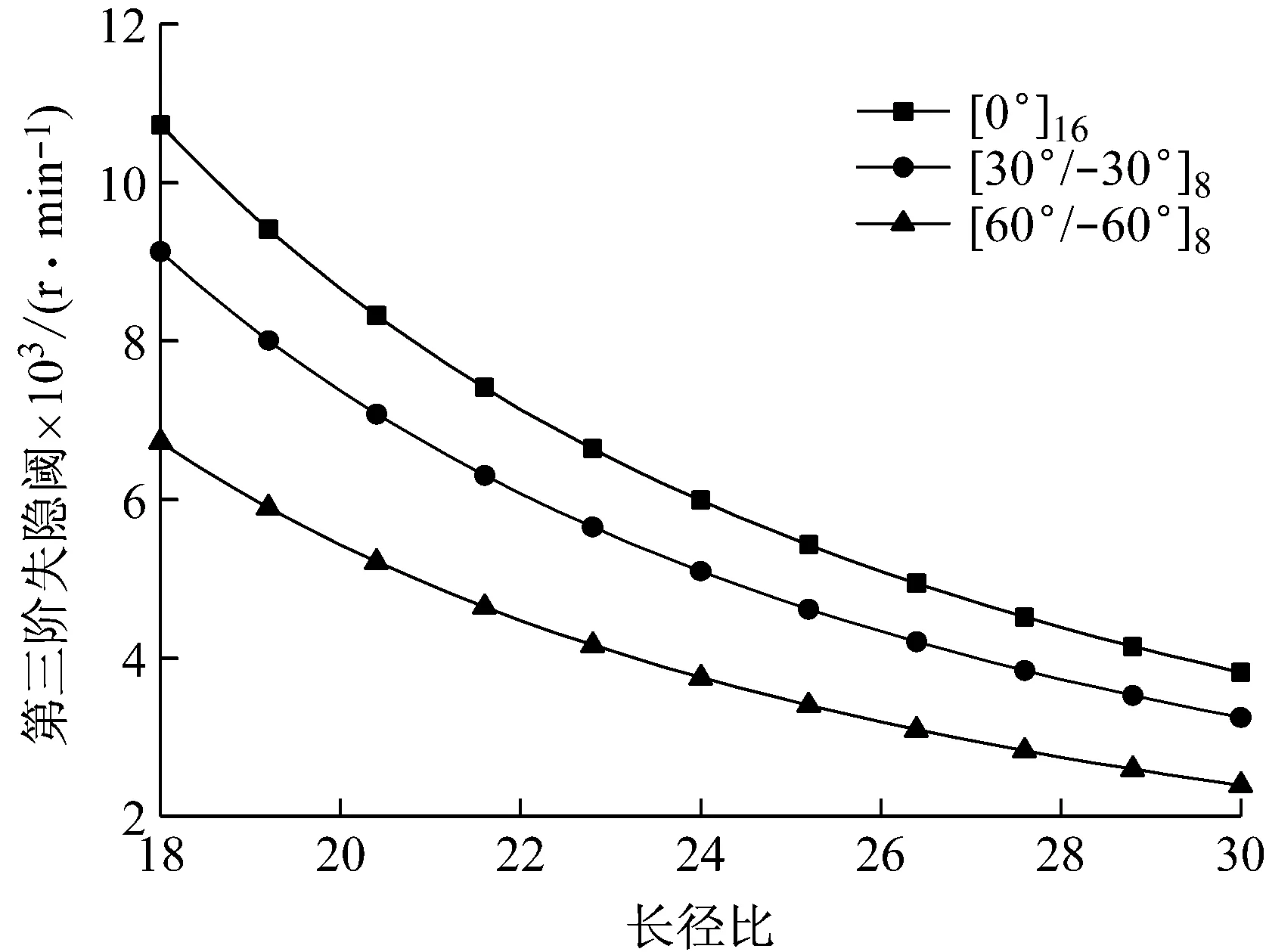
圖3表示旋轉復合材料軸的前三階失穩閾隨長徑比的變化曲線，其中也顯示出鋪層角的影響。這些曲線圖2的結果是相對應。值得說明的是，由于臨界轉速與失穩閾相同，當旋轉復合材料軸一旦超過臨界轉速進入超臨界范圍，就會產生不穩定自激振動。

3 非線性偏微分方程的離散化

為了研究旋轉復合材料軸的動力學特性，首先將彎-彎耦合非線性偏微分方程組(34)和(35)化為常微分方程組進行數值積分。由于本文并不打算考慮內共振的情況，為此，取單模態做近似處理，采用Galerkin法進行離散化。簡支復合材料軸的彎曲位移v(x,t)和w(x,t)可近似表示為

(47)

其中,n=1,2，…。

將式(47)代入運動方程式(34)和(35)，化簡得彎-彎耦合非線性常微分方程組

(a) 第一階

(b) 第二階

(c) 第三階

Fig.2 First three instability thresholds versus ply angle for different length aspect ratios

(48)

(a) 第一階

(b) 第二階

(c) 第三階

Fig.3 First three instability thresholds versus length aspect ratio for different ply angles

(49)

4 非線性自由振動響應與穩定性

(1) 鋪層角的影響

復合材料軸的基本參數仍然采用計算臨界轉速和失穩閾所使用的參數, 取模態階數n=1。為了研究鋪層角的影響，取長徑比L/d=20，轉速Ω=809 r/min，鋪層角分別為0°、30°、60°，采用四階Runge-Kutta法進行數值仿真，獲得軸中點位置的彎曲自由振動時間響應圖v(L/2,t)和w(L/2,t)，相平面圖和功率譜圖，如圖4～6所示。結果表明，在轉速不變的情況下，鋪層角分別為0°、30°和60°的復合材料軸的響應，分別是衰減振動(漸進穩定)、等幅振動(臨界穩定)和自激振動(不穩定)。原因在于，利用式(43)計算得到三個鋪層角對應的第一階臨界轉速和失穩閾分別為950 r/min，809 r/min和596 r/min，與之相對應的復合材料內阻分別大于0(耗散振動能量)，等于0(振動能量不耗散)和小于0(自激振動)。從功率譜圖來看，上述3種情況均屬于單頻振動；與0°和30°鋪層角對應的運動是小振幅線性振動，而與60°鋪層角對應的運動是失穩導致的穩態大振幅極限環振動(見(b)相平面圖)。事實上，具有負阻尼的線性自治系統的自由振動響應是發散的，而對于具有負阻尼非線性自治系統，非線性剛度的存在對自由振動振幅起限制的作用，自由振動響應由此不會無限增長，而是最終達到穩態的極限環振動。

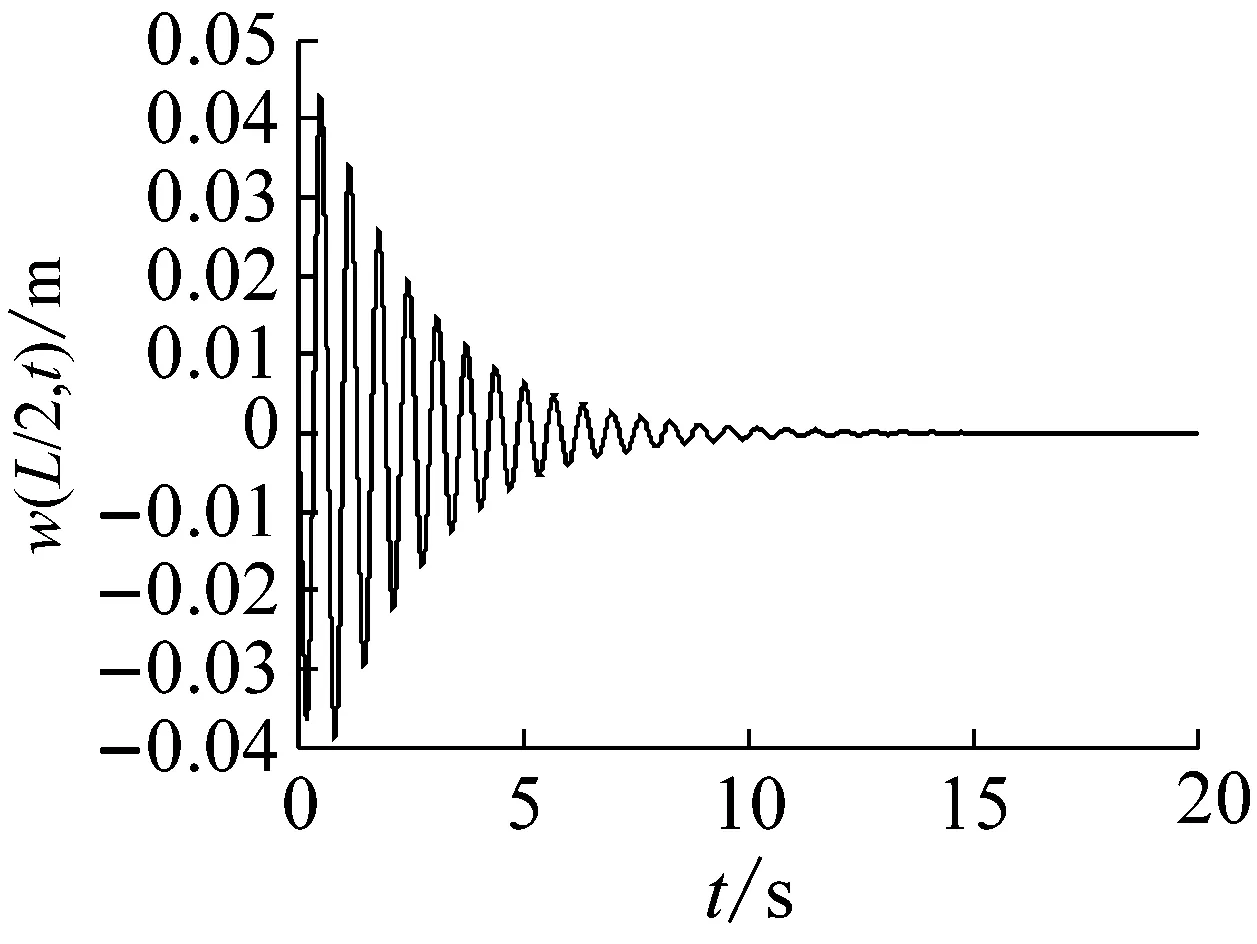
(a) 時間響應圖

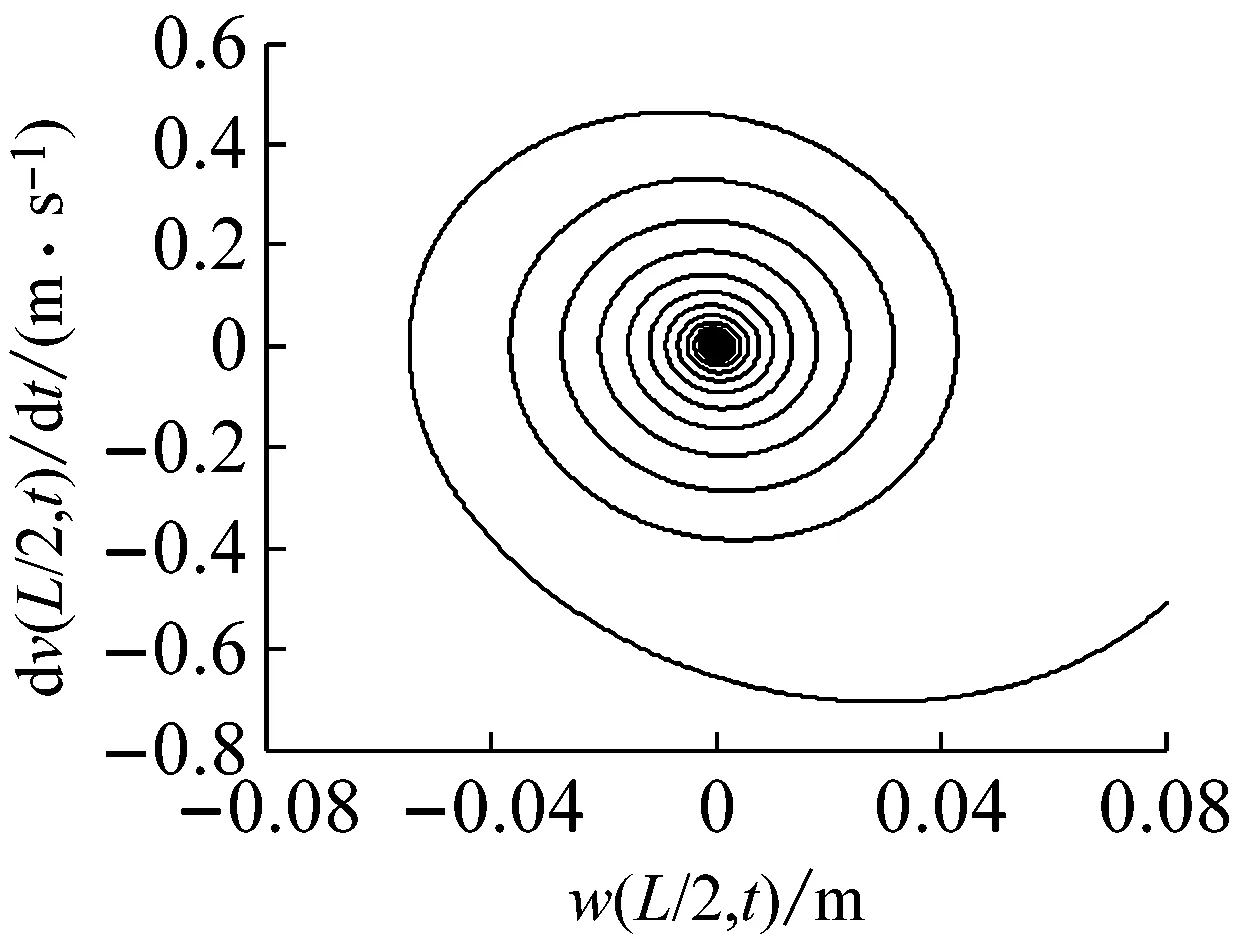
(b) 相平面圖

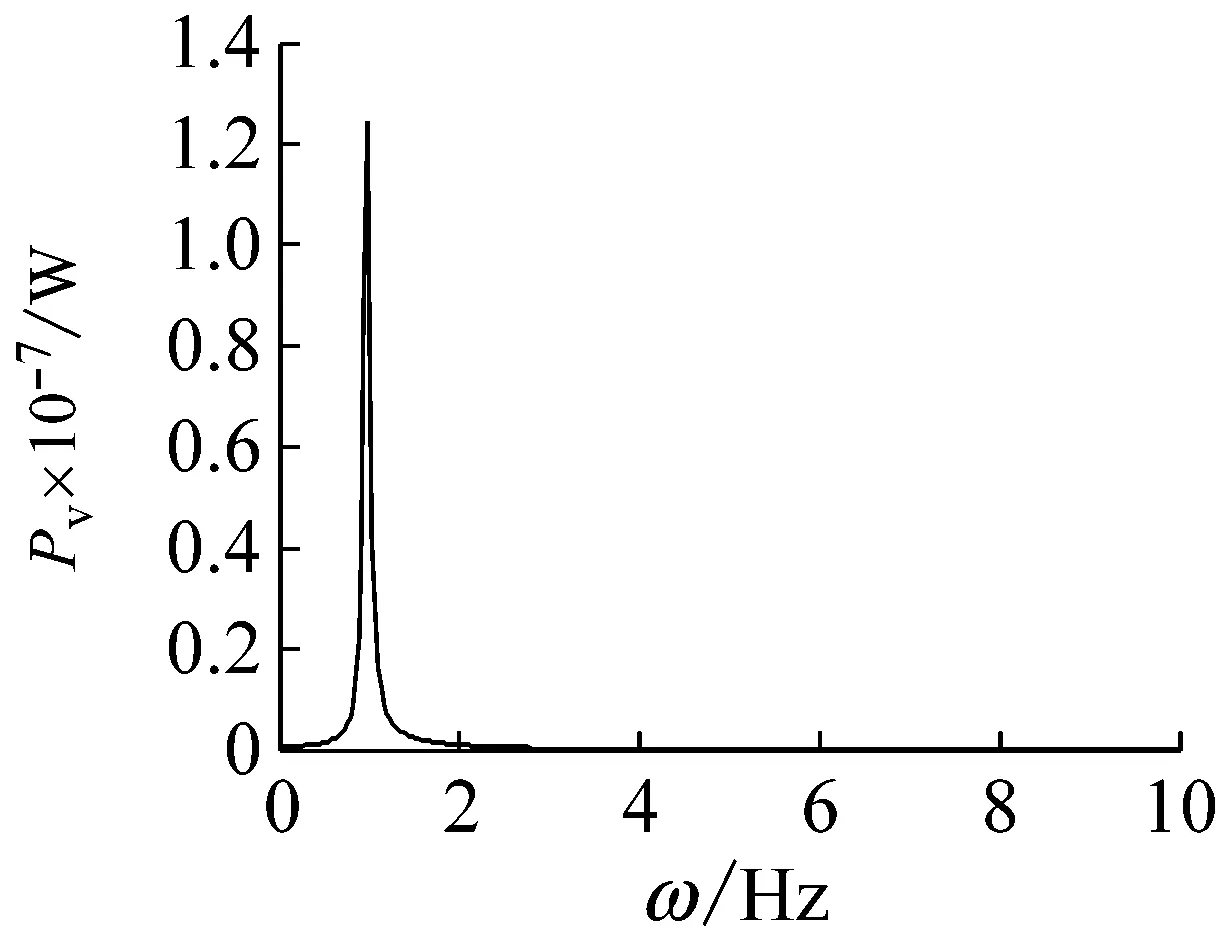
(c) 功率譜圖

(a) 時間響應圖

(b) 相平面圖

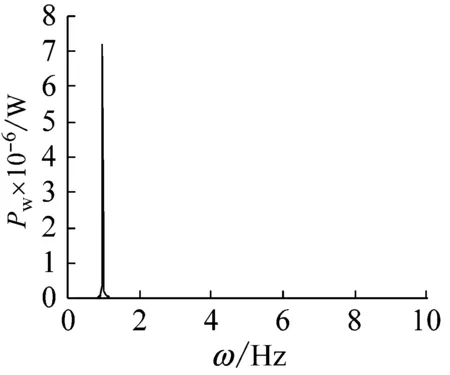
(c) 功率譜圖

(2) 長徑比的影響

為了研究長徑比的影響，我們取鋪層角30°，轉速Ω=809 r/min，長徑比分別為18，20和30，得到復合材料軸的動力學響應數值結果，如圖7～9所示。結果表明，轉速固定不變的情況下，隨著長徑比的增加，復合材料軸的運動表現出漸進穩定的、臨界穩定的和不穩定自激振動的演變過程，與此對應的第一階失穩閾分別是999 r/min，809 r/min和359 r/min，依次大于、等于和小于給定的轉速Ω=809 r/min，對應的內阻分別大于0，等于0和小于0，因此展示出三種不同的動力學響應特性。

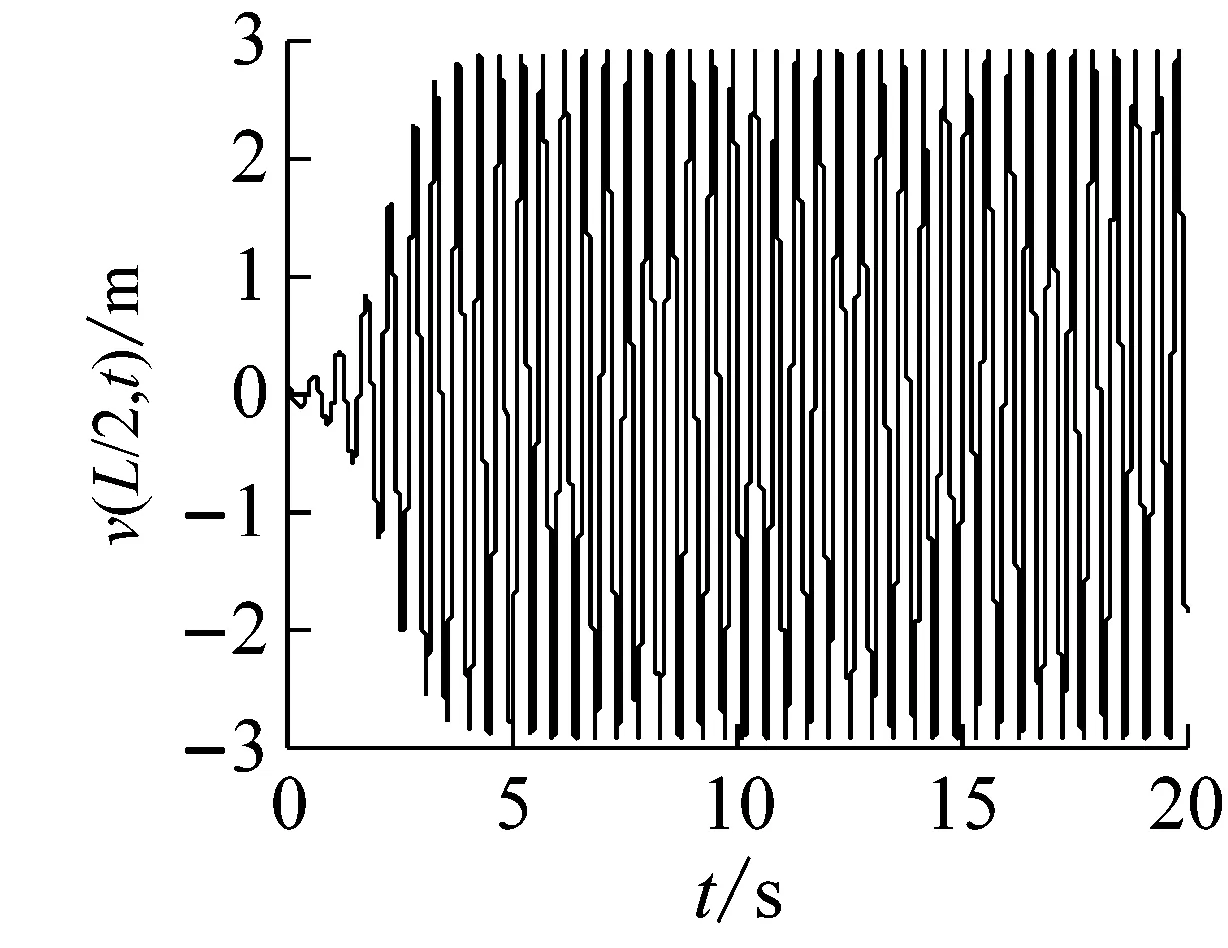
(a) 時間響應圖

(b) 相平面圖

(c) 功率譜圖

圖6 復合材料軸的自由振動響應(鋪層角為60°)

Fig.6 The free vibration response of a composite shaft(ply angle 60°)

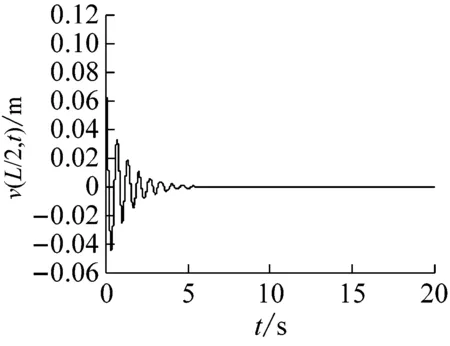
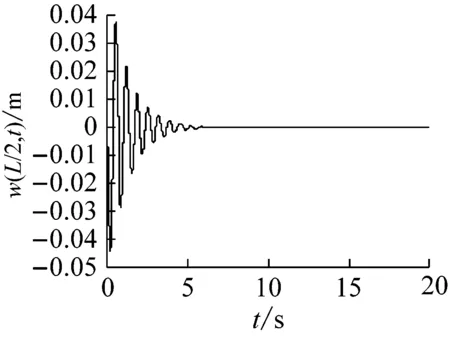
(a) 時間響應圖

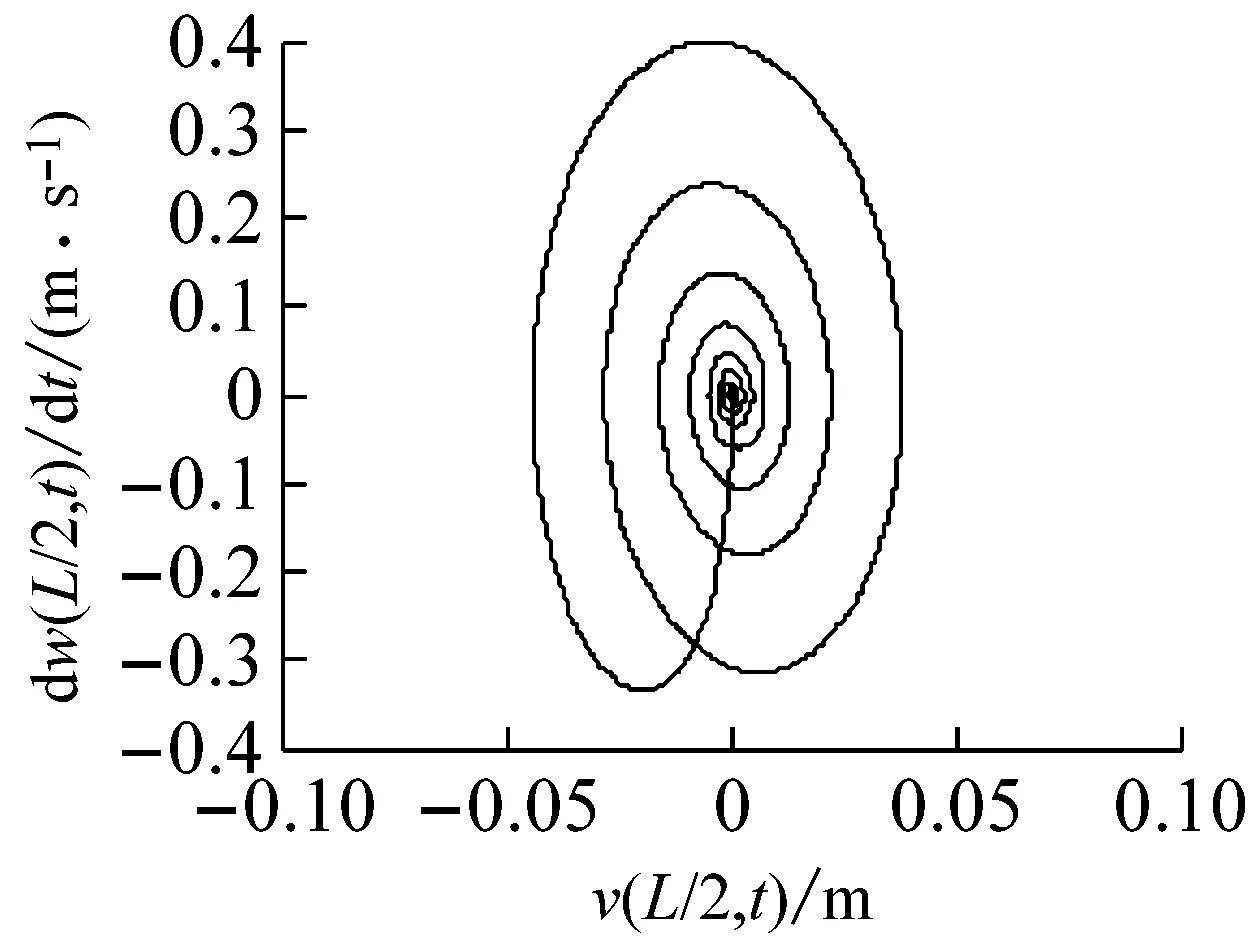
(b) 相平面圖

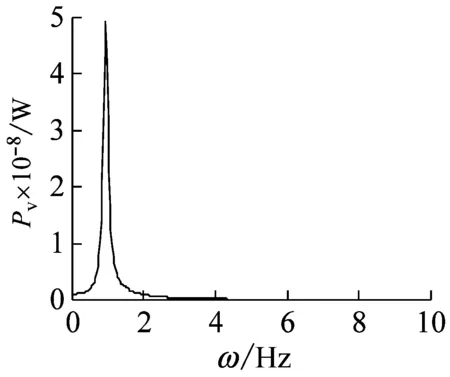
(c) 功率譜圖

圖7 復合材料軸的自由振動響應(長徑比為18)

Fig.7 The free vibration response of a composite shaft(ratio of length over outer radius 18)

(3) 鋪層方式的影響

取長徑比L/d=30，轉速Ω=391.06 r/min，鋪層方式分別取[0°]16，[±60°]8和[90°2/0°12/45°/-45°]，對應的旋轉復合材料軸的自由振動響應和穩定性仿真結果，如圖10～12所示。結果表明，在給定的轉速下，與鋪層方式[0°]16和[90°2/0°12/45°/-45°]對應的響應是穩定和臨界穩定的，而對應于鋪層方式[±60°]8的響應，由于已經失去了穩定性，表現為大振幅的穩態極限環振動。原因是在三種鋪層方式中，[±60°]8對應的第一階失穩閾最小，為264.49 r/min([0°]16和[90°2/0°12/45°/-45°]對應的第一階失穩閾分別是421.94 r/min和391.06 r/min)，因此，[±60°]8是上述三種鋪層方式中相對更容易產生內阻失穩的鋪層方式，從運動穩定性的角度來講，顯然也最不適合于在超臨界狀態下使用。

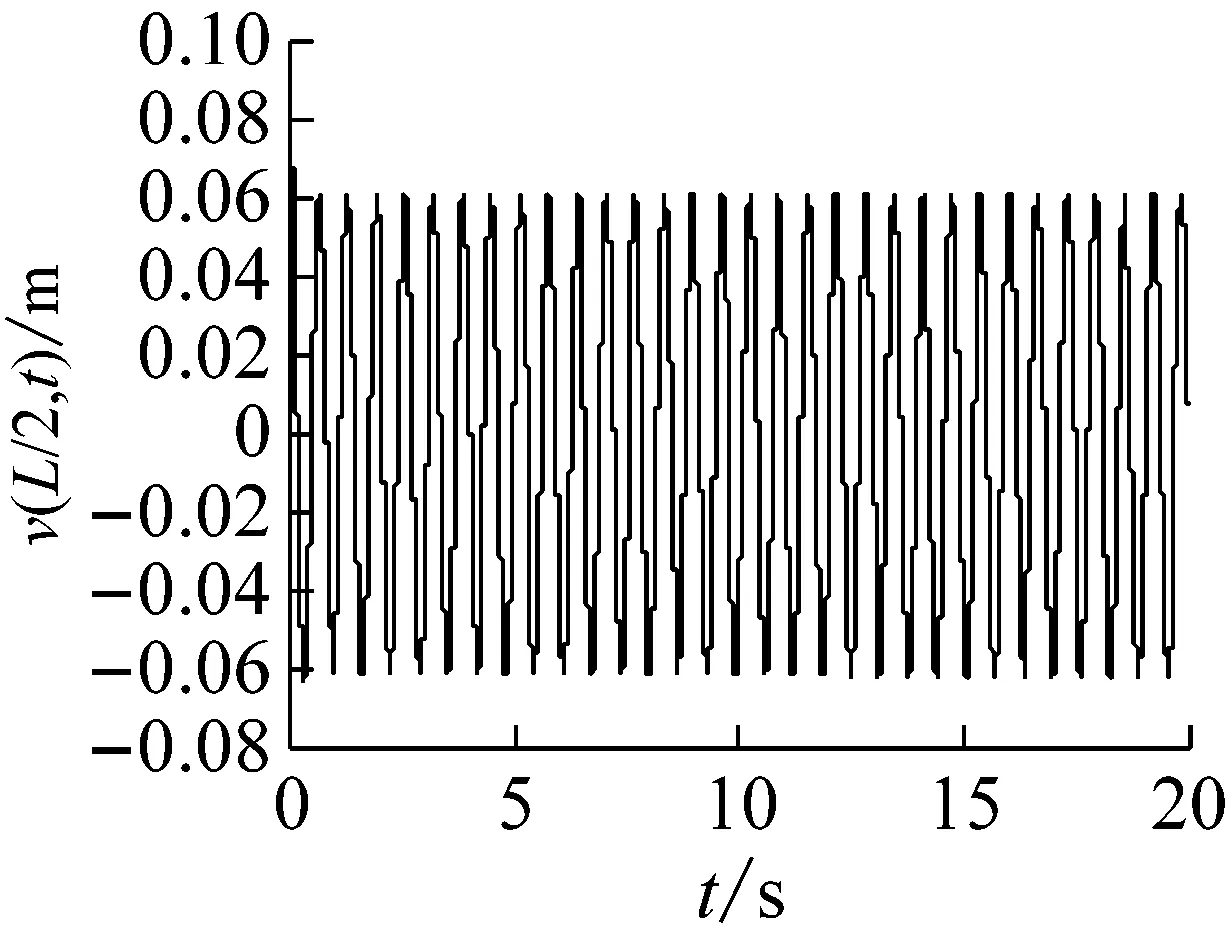
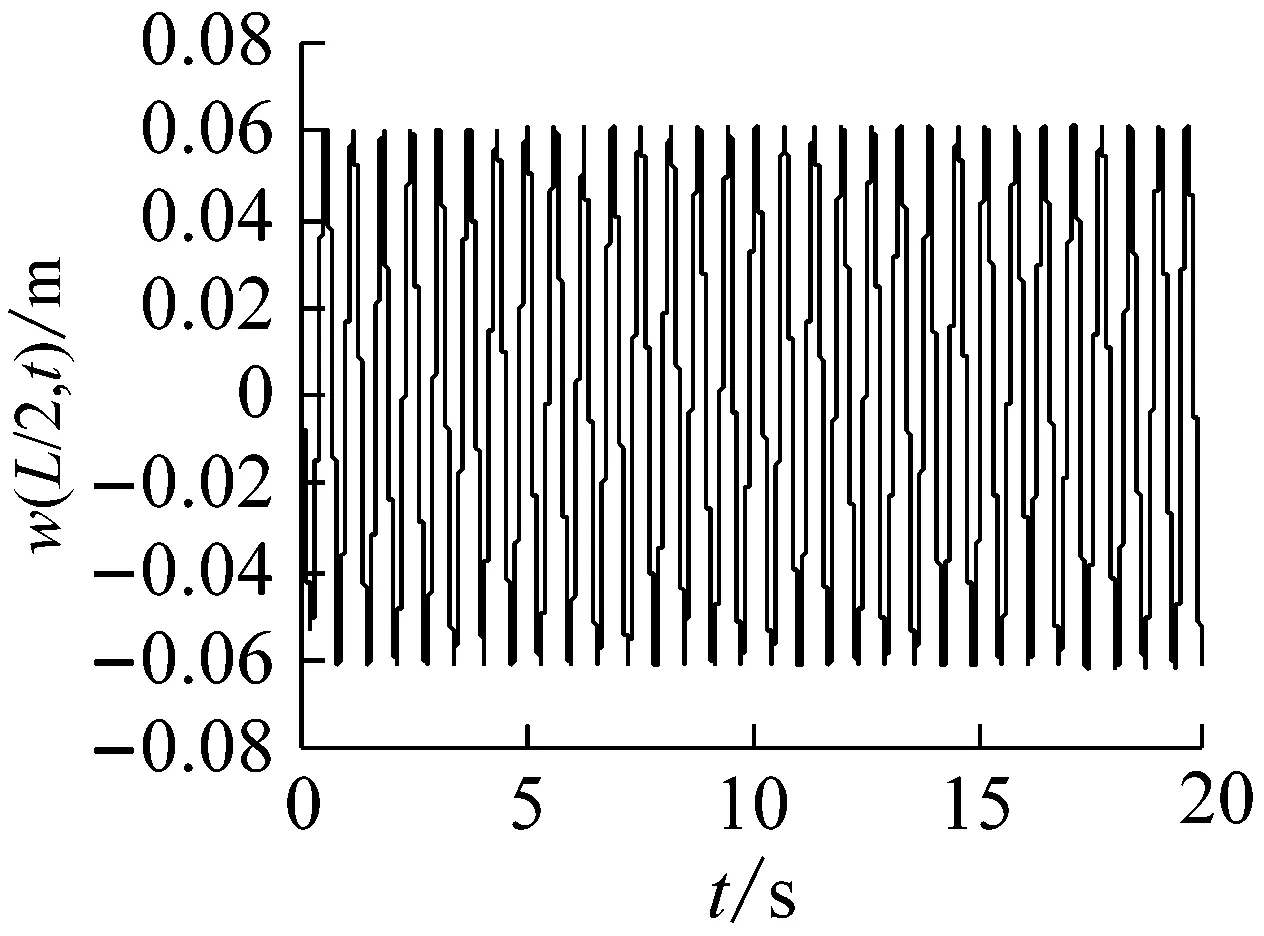
(a) 時間響應圖

(b) 相平面圖

(c) 功率譜圖

(a) 時間響應圖

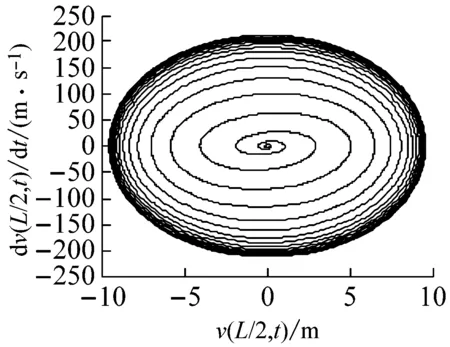
(b) 相平面圖

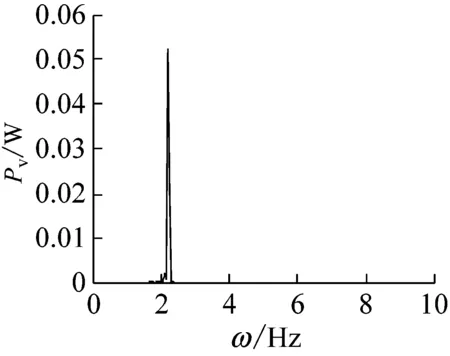
(c) 功率譜圖

圖9 復合材料軸的自由振動響應(長徑比為30)

Fig.9 The free vibration response of a composite shaft(ratio of length over outer radius 30)

5 結 論

研究了簡支旋轉復合材料軸的非線性自由振動與失穩特性。采用軸向不可伸縮復合材料大變形梁進行結構建模，其中包括曲率非線性和慣性非線性的影響，同時也利用復合材料的黏彈性耗散特性描述材料的內阻。針對線性化方程，采用特征值法研究了彎曲-彎曲耦合振動的臨界轉速與穩定邊界，采用四階Runge-Kutta法對非線性運動方程進行數值積分。主要結論如下：

(1) 由于本文模型只考慮復合材料內阻而不包含外阻尼，所以臨界轉速和失穩閾是相等的，這表明，旋轉復合材料軸一旦進入超臨界區就會產生內阻失穩。

(2) 在亞臨界區內，復合材料內阻大于0，對轉子自由振動的能量產生耗散和抑制的作用；當轉速等于臨界轉速時，復合材料內阻等于0，不耗散能量，轉子系統是臨界穩定的；在超臨界區內，復合材料內阻小于0，提供振動能量，轉子系統是不穩定的，將產生自激振動。

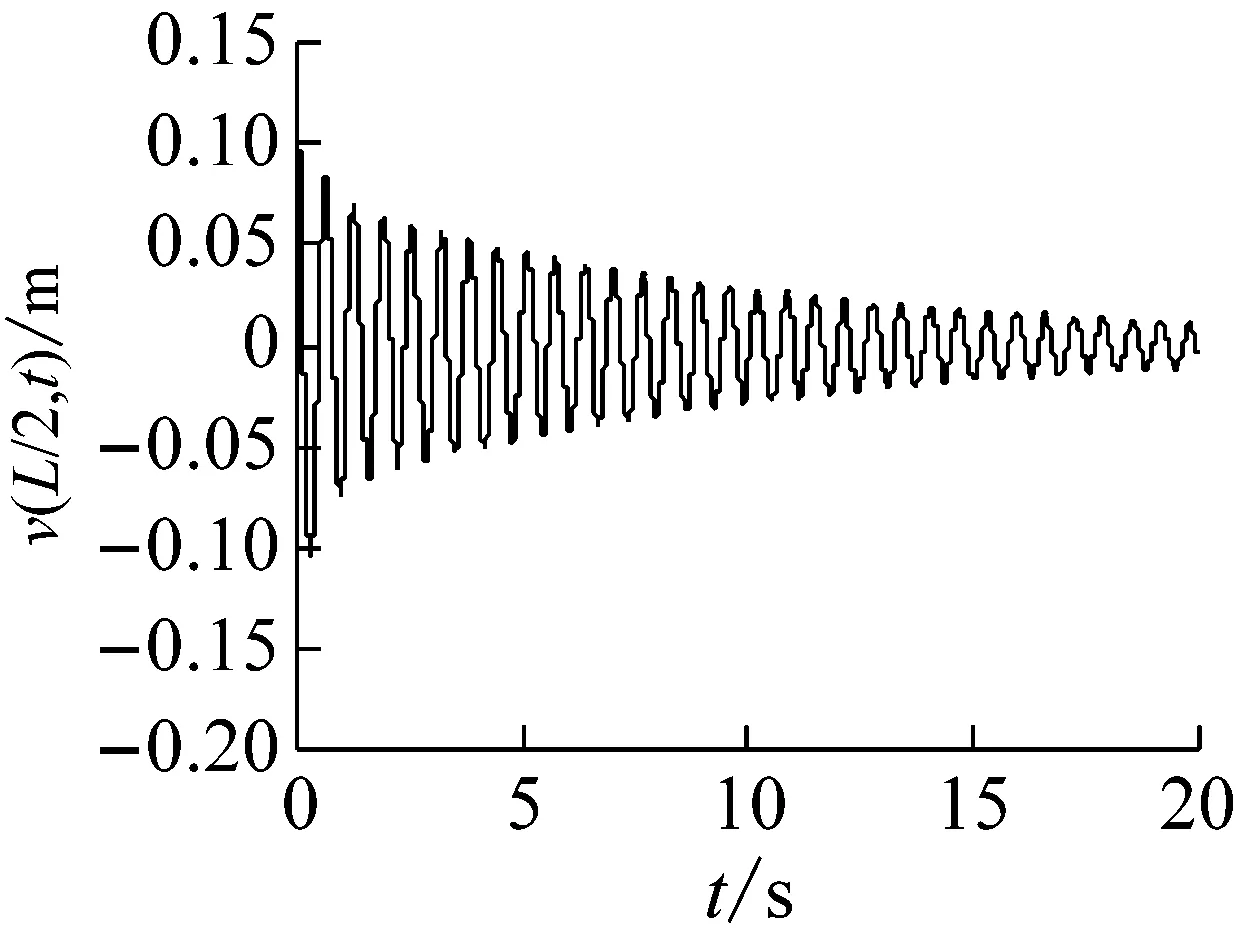
(a) 時間響應圖

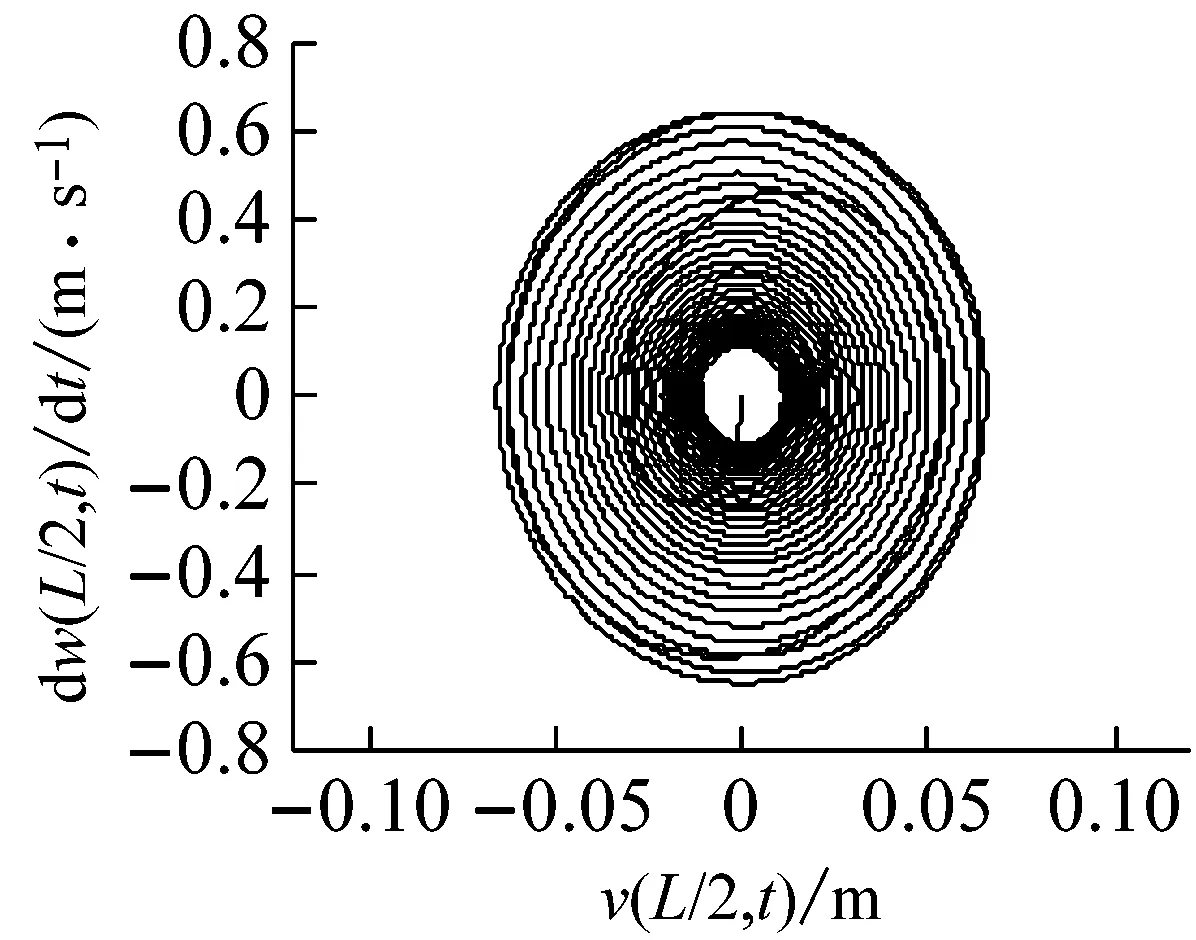
(b) 相平面圖

(c) 功率譜圖

圖10 復合材料軸的自由振動響應(鋪層方式[0°]16)

Fig.10 The free vibration response of a composite shaft(stacking sequence [0°]16)

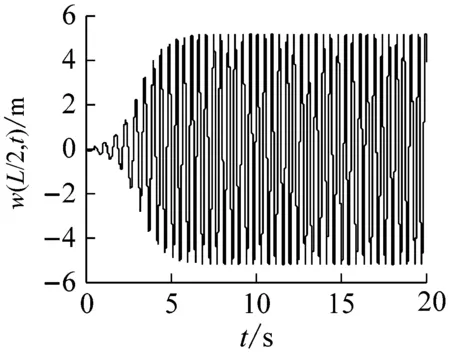
(a) 時間響應圖

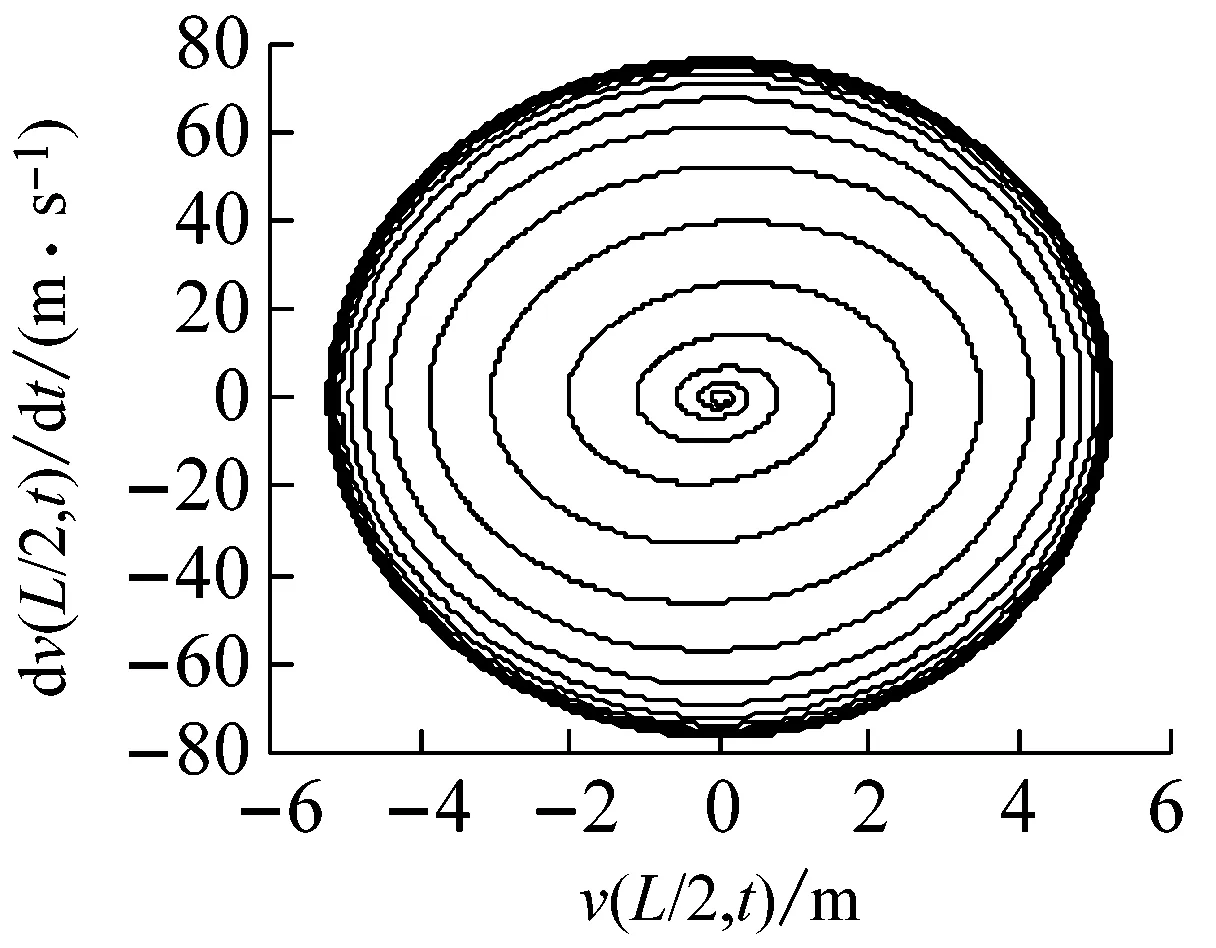
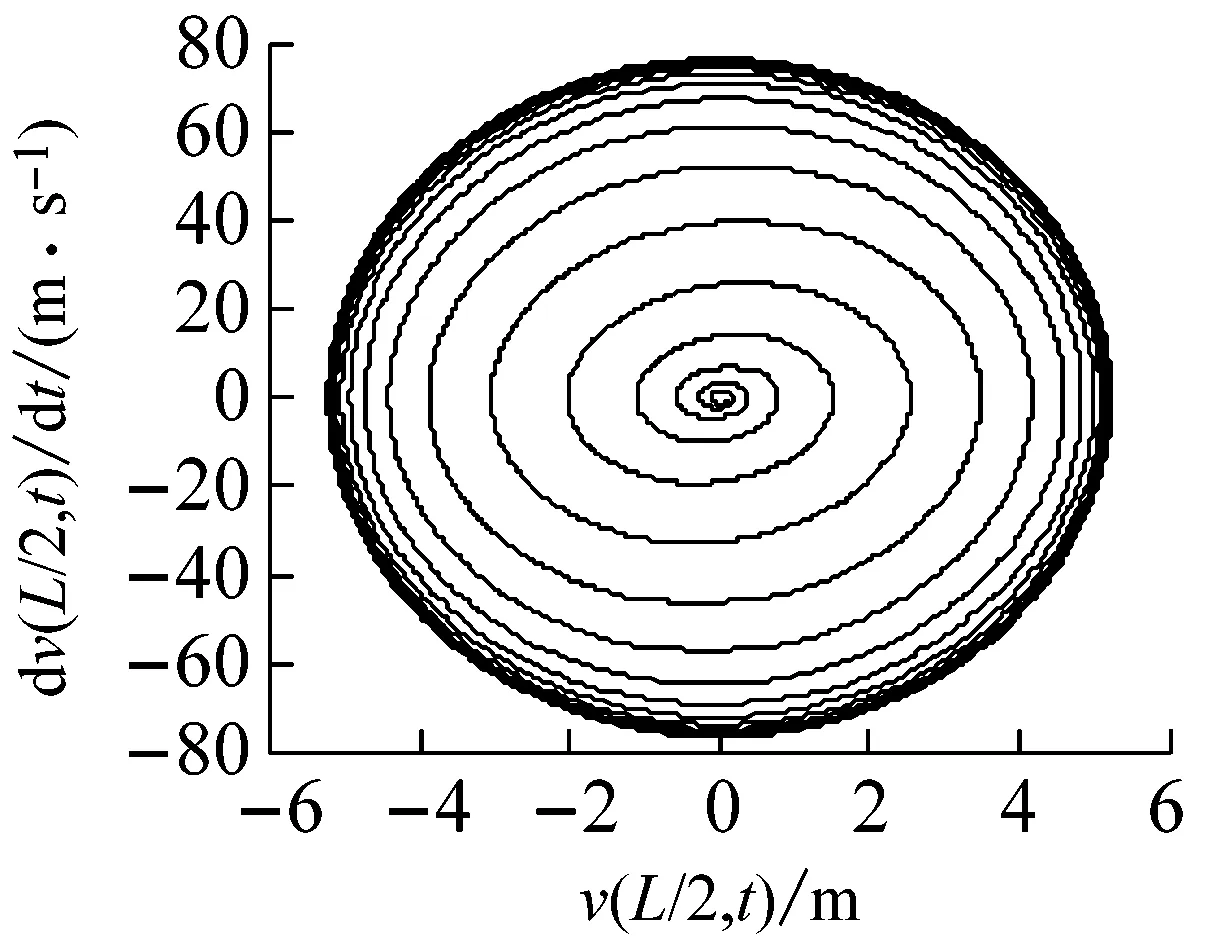
(b) 相平面圖

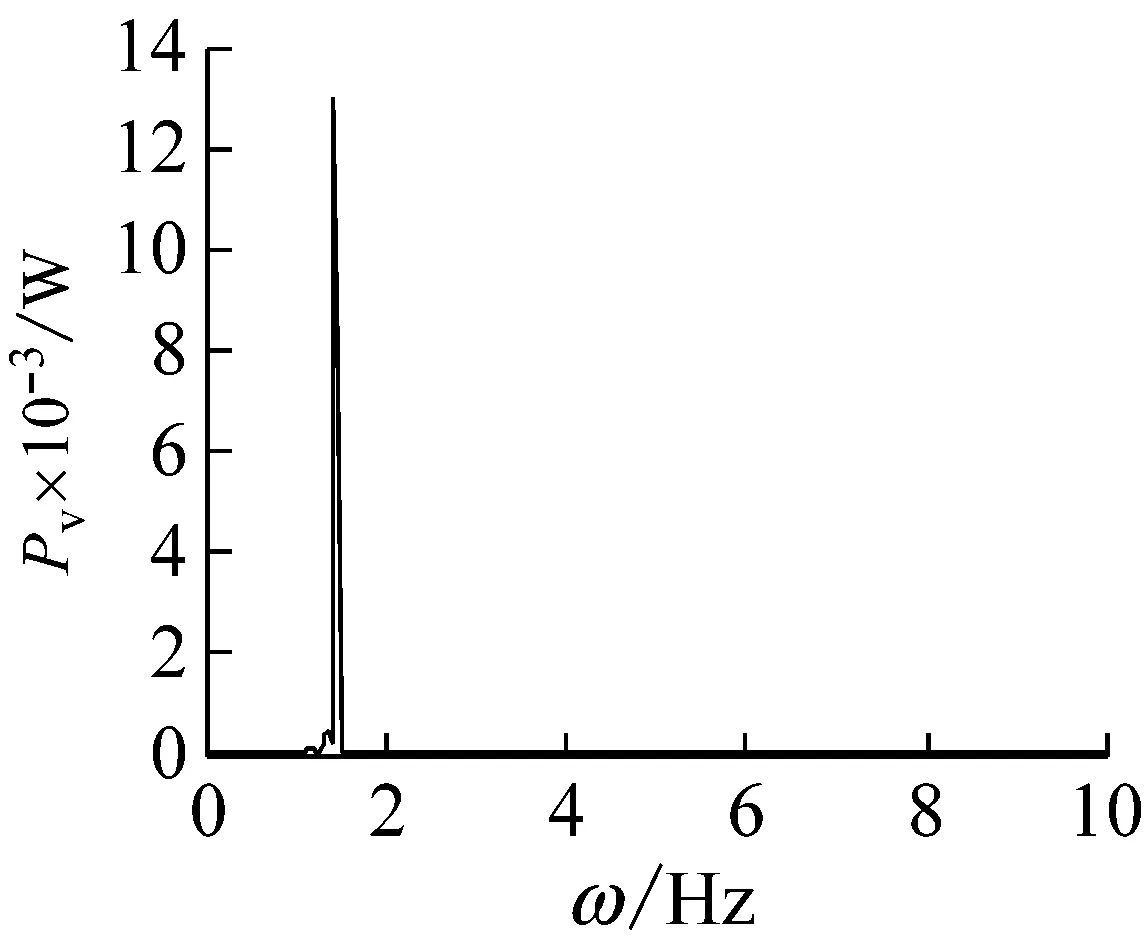
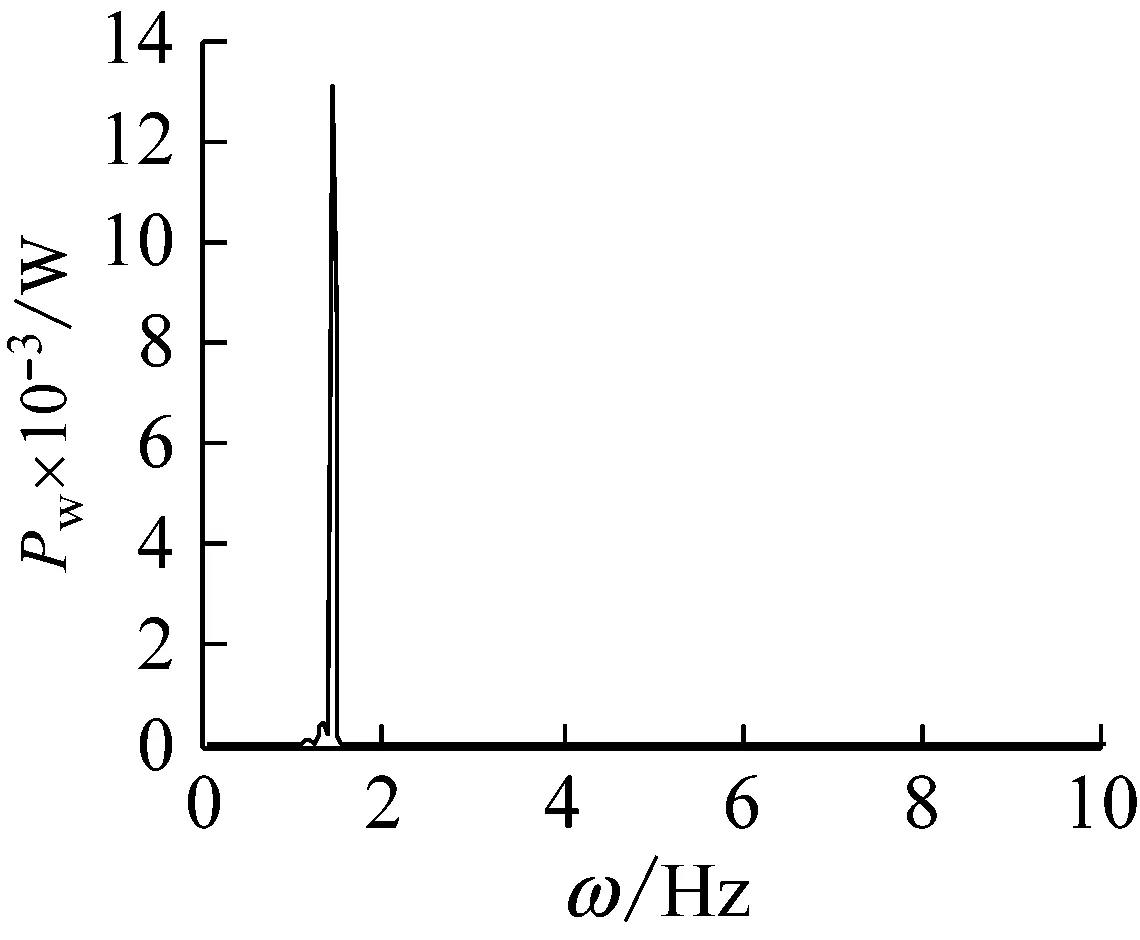
(c) 功率譜圖

圖11 復合材料軸的自由振動響應(鋪層方式[±60°]8)

Fig.11 The free vibration response of a composite shaft(stacking sequence [±60°]8)

(3) 在轉速固定的情況下，隨著鋪層角的增加，復合材料轉子系統的運動可能從穩定變為不穩定，會出現大振幅的穩態極限環振動。這是由于失穩閾隨著鋪層角的增加而減小。類似地，隨著長徑比的增加，復合材料轉子系統的運動也可能從穩定變為不穩定，發生極限環振動。同樣，此外，鋪層方式對復合材料轉子系統穩定性與非線性振動特性也會產生明顯的影響。

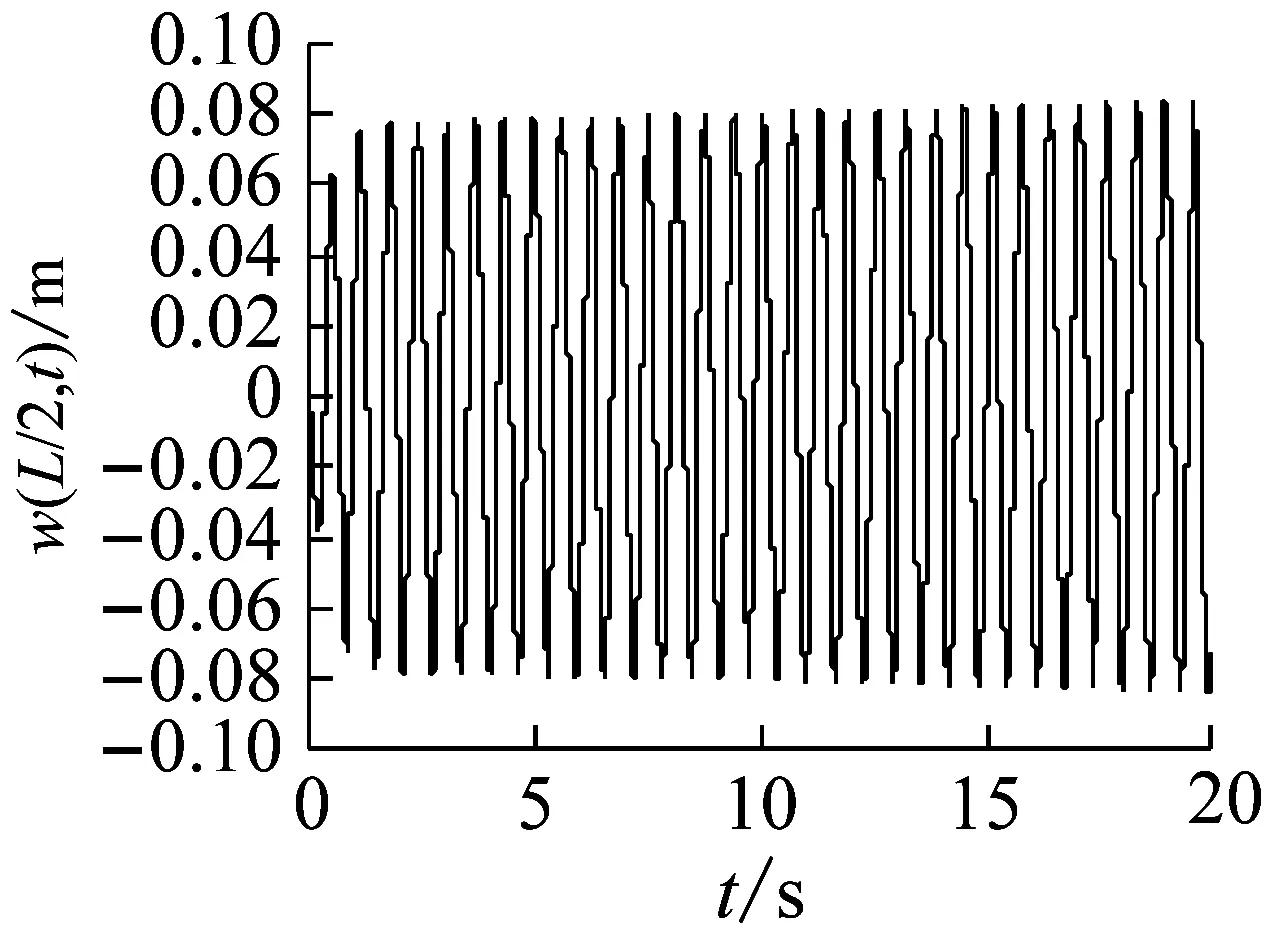
(a) 時間響應圖

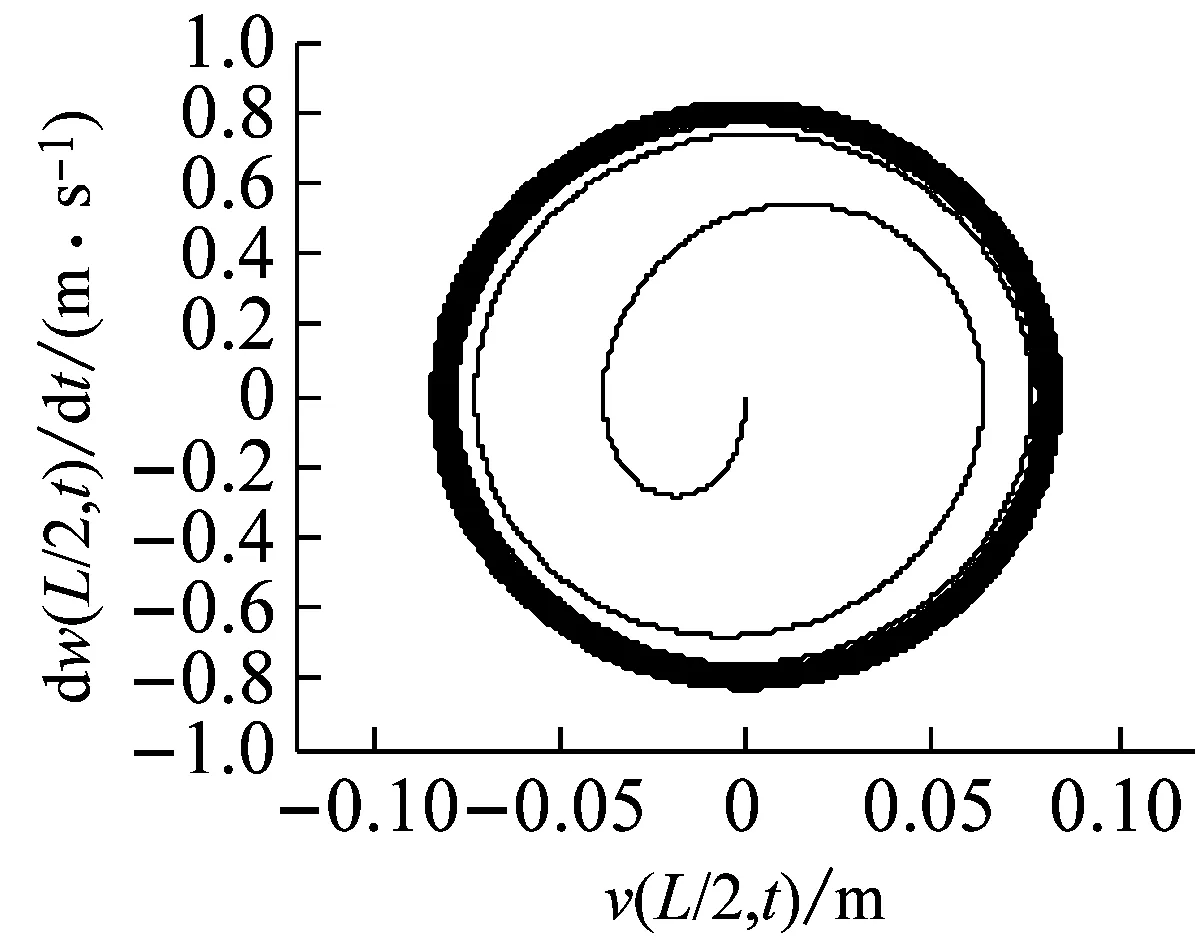
(b) 相平面圖

(c) 功率譜圖

圖12 復合材料軸的自由振動響應(鋪層方式[90°2/0°12/45°/-45°])

Fig.12 The free vibration response of a composite shaft(stacking sequence [90°2/0°12/45°/-45°])

[1] ISHIDA Y, IKEDA T,YAMAMOTO T. Nonlinear forced oscillations caused by quartic nonlinearity in a rotating shaft system[J].ASME J Vib Acoust, 1990,112:288-297.

[2] ISHIDA Y, IKEDA T,YAMAMOTO T, et al. Internal resonance in a rotating shaft systems: the coincidence of two critical speeds for subharmonic oscillations of the order 1/2 and synchronous backward precession[J].Bull JSME, 1986, 29:1564-1571.

[3] ISHIDA Y, IKEDA T, YAMAMOTO T, et al. Nonstationary vibration of a rotating shaft with nonlinear spring characteristics during acceleration through a critical speed[J]. JSME Int J C, 1992, 35:360-368.

[4] CVETICANIN L. Large in-plane motion of a rotor[J]. Journal of Vibration and Acoustics, 1998,120 (1): 267-271.

[5] HOSSEINI S A A, KHADEM S E. Free vibrations analysis of a rotating shaft with nonlinearities in curvature and inertia[J]. Mechanism and Machine Theory, 2009,44:272-288.

[6] RIZWAN SHAD M R, MICHON G, BERLIOZ A. Modeling and analysis of nonlinear rotordynamics due to higher order deformations in bending[J].Applied Mathematical Modelling, 2011, 35:2145-2159.

[7] SHAHGHOLI M, KHADEM S E. Primary and parametric resonances of asymmetrical rotating shafts with stretching nonlinearity[J]. Mechanism and Machine Theory, 2012,51:131-144.

[8] KHADEM S E, SHAHGHOLI M, HOSSEINI S A A. Two-mode combination resonances of an in-extensional rotating shaft with large amplitude[J]. Nonlinear Dyn, 2011,65:217-233.

[9] SARAVANOS D A, VARELIS D, PLAGIANAKOS T S, et al. A shear beam finite element for the damping analysis of tubular laminated composite beams[J]. Journal of Sound and Vibration, 2006, 291:802-823.

[10] SINO R, BARANGER T N, CHATELET E, et al. Dynamic analysis of a rotating composite shaft[J].Composites Science and Technology, 2008, 68:337-345.

[11] REN Yongsheng, ZHANG Xingqi, LIU Yanghang, et al. An analytical model for dynamic simulation of the composite rotor with internal damping[J]. Journal of Vibroengineering, 2014, 16(8):4002-4016.

[12] SHAW J, SHAW S W. Instabilities and bifurcations in a rotating shaft [J]. Journal of Sound and Vibration,1989,132(2):227-244.

[13] LUCZKO J. A geometrically non-linear model of rotating shafts with resonance and self-excited vibration [J]. Journal of Sound and Vibration,2002, 255(3):433-456.

[14] SHAW J, SHAW S W. Non-linear resonance of an unbalanced rotating shaft with internal damping [J]. Journal of Sound and Vibration,1991,147(3):435-451.

[15] 陳予恕,丁千.非線性轉子動力學的穩定性和分岔[J].非線性動力學報,1996,3(1):13-22.

CHEN Yushu, DING Qian.A study on stability and bifurcation of nonlinear rotor dynamics[J].Journal of Nonlinear Dynamics in Science and Technology,1996,3(1):13-22.

[16] 曹樹謙. 高維復雜轉子系統非線性動力學的若干現代問題研究[D].天津:天津大學,2003.

[17] ISHIDA Y, YAMAMOTO T. Forced oscillations of a rotating shaft with nonlinear spring characteristics and internal damping (1/2 order subharmonic oscillations and entrainment)[J].Nonlinear Dyn,1993, 4:413-431.

[18] HOSSEINI S A A. Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaft with internal damping[J].Nonlinear Dyn, 2013,74:345-358.

[19] 任勇生，張興琦，代其義. 旋轉復合材料薄壁軸的不平衡非線性彎曲振動[J].振動與沖擊，2015，34(3):150-155.

REN Yongsheng, ZHANG Xingqi, DAI Qiyi. Nonlinear bending vibration of an unblanced rotating composite thin-walled shaft[J]. Journal of Vibration and Shock,2015,34(3):150-155.

[20] REN Yongsheng, ZHANG Yuhuan,DAI Qiyi. Primary resonance of a rotating composite shaft with geometrical nonlineary[J].Journal of Vibroengineering,2015,17(4):1694-1706.

[21] CRESPO DA SILVA M R M, GLYNN C C. Nonlinear flexural-flexural-torsional dynamics of inextensional beams. II. Forced motions[J].Journal of Structural Mechanics,1978, 6:449-461.

[22] NAYFEH A H, PAI P F. Linear and nonlinear structural mechanics[M]. New York: Wiley Interscience, 2004.