基于階次跟蹤的直升機旋翼動平衡調整分析研究
吳國寶 易暉 湯永


摘要
為實現直升機旋翼系統在高速旋轉過程中動平衡調整建議的快速計算,提出了一種基于階次跟蹤原理的動平衡調整分析方法。該方法,利用階次跟蹤原理對旋翼系統的振動信號進行快速分析得到旋翼的動平衡值,有效克服了傳統頻譜分析方法在分析非平穩信號中存在的頻率混疊及能量泄露等問題;在此基礎上,利用最多一次試配重結果快速計算出動平衡調整建議。整個過程通過軟件算法實現旋翼動平衡值及調整建議的快速計算,大大降低了使用成本及對地勤工作人員的使用要求;同時,該方法也具有較好的通用性和可移植性,針對不同機型不同架次的直升機只需更改相應的配置文件即可。試驗結果表明,使用該方法調整直升機旋冀的平衡值取得了較理想的效果。
【關鍵詞】階次跟蹤 直升機 旋翼 動平衡 調整
1 引言
直升機旋翼作為直升機的重要組成部件,為直升機的飛行提供所需的升力和推進力,同時也是直升機的一個主要振動源,其旋翼槳葉質量不平衡和氣動不平衡是引起機體振動加劇的常見原因。為了降低直升機振動,確保飛行安全,需定期對旋翼系統進行動平衡調整。常見的直升機旋翼動平衡調整多是通過調整每片槳葉的槳轂配重,使得振動減小到允許水平,從而確保機組人員和乘客的舒適性。如何快速有效地獲得動平衡調整建議,減小動平衡的調整次數,已成為直升機振動研究領域的一個重要研究方向。
目前普遍采用的直升機旋翼動平衡調整方法主要有:
(1)通用動平衡測量儀法。這類方法首先,利用Vibrex2000、Model 2020等通用動平衡測量儀,測得旋翼的動平衡值;然后,地勤工作人員依據工作經驗對相應支臂的配重進行增減,以達到調整目的。這類方法使用靈活、通用性較好;但對配重量的調整存在較大的盲目性,調整精度及調整次數嚴重依賴于地勤工作人員的經驗及對飛機性能的了解程度;
(2)特定機型專用動平衡測量儀法。這類方法針對特定機型開發專用設備(如S-70C直升機采用的1720監測儀),在研制階段通過大量的試驗數據積累,將特定的調整算法內置到相關軟件中,能在得到旋翼動平衡測量結果的同時直接給出調整建議;但通用性差,只適合特定機型的專檢。
為此,本文提出了一種基于階次跟蹤的直升機旋翼動平衡調整分析方法。該方法主要由兩大部分構成,第一部分,利用階次跟蹤分析方法計算得到旋翼的動平衡值;第二部分,利用加載一次試配重后得到的兩次旋翼動平衡值,計算出旋翼動平衡調整建議。該方法通過軟件實現旋翼動平衡值及調整建議的計算,有效降低了地勤維護人員的使用難度及直升機開車次數,同時該方法也具有較好的通用性和可移植性。
2 原理與步驟
2.1 階次跟蹤計算動平衡值
2.1.1 階次跟蹤
當直升機旋翼系統在高速旋轉過程中其轉速在嚴格意義上是波動的,轉速越高波動就越大,目標頻率成分受轉速的影響而不斷發生改變。此時若仍采用傳統的頻譜分析方法進行分析,會產生明顯的頻率混疊和能量泄露。為克服以上問題,更好地對直升機旋翼動平衡值進行有效分析,本文采用階次跟蹤分析方法來計算旋翼的動平衡值。
階次跟蹤分析源于角域重采樣理論,即旋翼每轉過一定角度,重采樣一次,這樣便實現了對轉速的跟蹤采樣。單位時間內轉速越快采樣點數越多,轉速越慢采樣點數越少,保證了無論轉速高低都能進行整周期采樣。再對重采樣后的數據進行傅里葉變換便可獲得清晰的階次譜。
階次定義為:
Ω=循環振動次數/轉(階)
信號的階次分量與頻率成分的關系可表示為:
式中,Ω表示階次,f為信號的頻率,n為參考軸轉速(r/min)。
階次分析得到的結果相對于頻譜來說叫階次譜,兩者在數學意義上是一致的,但在物理意義上又有所不同。階次分辨率△Ω定義為采樣階次Ω,定義為:
Nyquist階次ΩN,即可分析的最高階次量定義為:
上式中,N為重采樣點數,θ0為恒定重采樣角度間隔。
2.1.2 等角度重采樣時刻計算
要對時域采集的旋翼振動信號進行階次跟蹤重采樣,首先需要確定等角度發生的時刻序列。假設,旋翼系統在某個很短時間內是勻角加速度運動的,轉過的角度θ與時間t的關系可表示為:
式中,a0、a0、a1為待定系數。
假設,連續三個旋翼轉速脈沖到達時刻值為t1、t2、t3;相鄰兩個轉速脈沖之間轉過的角度2π=Δθ,則有:
將式(6)代入式(5)中,則有:
通過對式(7)的求解,便可求得任意角度θi(0≤θi≤2Δθ)所對應的采樣時刻ti,則重采樣時刻的基本計算公式為:
式中,ti為旋翼轉過角度為θi時所對應的時刻值。由于計算中采用了三個連續轉速脈沖來構造這個方程的,所以有(0≤θi≤2Δθ)。
2.1.3 旋翼振動信號階次重采樣
由于采集的旋翼振動信號是離散量信號,要利用2.1.2節得到的重采樣時刻對旋翼振動信號進行重采樣,需先對離散量信號進行擬合得到一條平滑的振動信號曲線,針對直升機旋翼的振動信號特征,本文采用一般線性插值對離散量進行線性擬合,然后再進行重采樣,則有下式成立:
式中,f(ti)為重采樣時刻對應的振動信號重采樣值;Δt0、Δt2為與ti相鄰的兩個時域采樣時刻,其對應的振動值分別為f(Δt0)、f(Δt2)。
在獲得旋翼振動信號階次跟蹤重采樣數據的基礎上,再利用短時傅里葉變換(Short-Time Fourier Transformation,STFT),便可求得旋翼的動平衡值。
綜上所述,本文所提方法,旋翼動平衡值的計算流程,如圖1所示、
2.2 動平衡調整建議計算
試配重法是現代轉子動平衡技術中,普遍采用的一種分析方法。利用該方法可在沒有任何數據積累的情況下,通過分析,直升機旋翼的初始動平衡值與加載一次試配重后,得到的動平衡值組成的矢量,以及配重量(包括配重質量及加載的加載點編號)三者之間的關系,便可得出旋翼動平衡調整需加載的重量及加載點編號。
2.2.1 試配重法
如圖2所示,o旋轉平面圓心;P2、P2分別表示初始動平衡值和加載試重后得到的動平衡值在旋轉平面內對應的位置;P1P2為加載試配重T0(單位為:g)后引起的動平衡值的變化量。則易知在旋轉平面內,初始旋翼動平衡值P1的動平衡調整量ΔT(單位為:g)為:
調整量△T的加載方向△e為:
2.2.2 動平衡調整建議計算
上述2.2.1節就試配重法原理進行了介紹,下面就如何利用試配重法,得到旋翼的動平衡調整建議進行簡要介紹。
如圖3所示,設A0為某架次直升機,首次開車時得到的動平衡值在旋轉平面上的對應點;試配重加載在001C號槳葉的加載點上,試配重質量為T(單位為:g);A1為再次開車后得到的動平衡值在旋轉平面上的對應點。
則的方向即為001C號槳葉加載點的方向,由于槳葉呈順時針旋轉,支臂配重加載點坐標軸的布局形式與槳葉一致,通過計算便可依次得到001A、001B、001D、001E號槳葉加載點在旋轉平面中的對應位置。在得到各槳葉加載點在旋轉平面的具體位置后,只需將分解到相鄰的兩片槳葉001C、001D上,通過計算便可得出槳葉初始不平衡點A0的動平衡調整建議。
如圖4所示,令,則有,故槳葉初始不平衡值在001C、001D號槳葉配重點上的調整量ΔTC、ΔTD分別為:
2.3 實施步驟
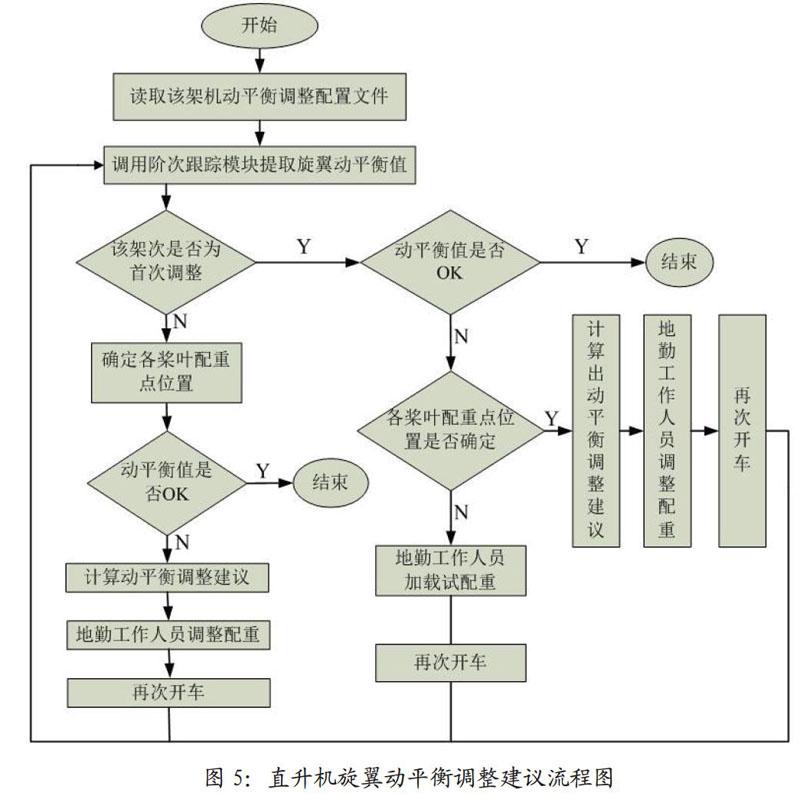
由以上2.1、2.2節描述可知,本文所提直升機旋翼動平衡調整分析方法流程示意圖,如圖5所示:
具體實施步驟為:
步驟1讀取該架次直升機的動平衡配置文件及傳感器采集的旋翼振動及轉速信號;
步驟2調用階次跟蹤分析模塊,獲得旋翼動平衡值;
步驟3判斷該架次直升機是否為首次動平衡調整,若是執行下一步,否則執行步驟7;
步驟4判斷此時動平衡值是否滿足用戶需求,若滿足則結束,否則執行下一步;
步驟5判斷槳葉配重加載點位置是否確定;若已確定,直接給出動平衡調整建議;若不確定,則地勤工作人員加載一次試配重;
步驟6加載試配重或建議配重后再次開車,執行步驟2;
步驟7確定各槳葉配重加載點在旋轉片面中的位置,并執行步驟4。
3 試驗及分析
為驗證本文所提方法在直升機旋翼動平衡調整分析中的有效性,分別在不同試驗條件下進行了兩次驗證試驗:第1次試驗,在中國直升機設計研究所綜合試驗室的旋翼錐體與動平衡仿真試驗臺上進行;第2次試驗,在中國飛行試驗研究院的某型直升機的試飛現場進行。
3.1 旋翼錐體與動平衡仿真試驗臺試驗
如圖6所示,為中國直升機設計研究所綜合試驗室的旋翼錐體與動平衡仿真試驗臺,該試驗臺能有效模擬多種類型旋翼系統在不同轉速、不同振動量下的旋翼動平衡效果。
本試驗選用的方位角轉速傳感器的型號為:西安西靈Y/GZ-93;振動加速度傳感器的型號為:PCB354CO3;為最大限度地模擬機上環境,采集振動及轉速信號的設備為某型機HUMS計算機。
試驗以五片槳葉旋翼系統為研究對象進行。各槳葉配重加載點編號,以俯視呈順時針旋轉狀態依次為:1#、2#、3#、4#、5#;規定,動平衡值在0.11PS(inch per second)以下為滿足要求,試驗結果如表1所示
表1中,動平衡值“0.40@01:58”表示振動幅值為0.40IPS,相位為01:58即59°,以此類推;配重或調整建議“4#1.9g”表示在4號加載點上添加1.9g,“-”表示在相應加載點上減去對應重量。
從表1中可知,對于第1組試驗,由于首次測量的動平衡值不滿足要求,且槳葉配重加載點位置不確定,需加載試配重,通過試配重后動平衡正好滿足要求,此時不給出調整建議并結束;對于第2組試驗,在確定槳葉配重加載點位置后,由于試配重使動平衡值變大,故認為此次試配重無效,調整建議中應將相應配重位上的配重去除;對于第3組試驗,由于加載了試配重后使得動平衡值變小,認為加載的試配重是有效的,調整建議中試配重結果予以保留;對于第4組試驗,雖然首次測量動平衡值不滿足要求,但通過讀取配置文件信息能確定槳葉配重加載點的位置,此時便可據此直接給出動平衡調整建議。
表1所示在旋翼錐體與動平衡仿真試驗臺上進行的4組試驗均能將動平衡值調整到的使用要求以下,結果表明,本文所提直升機旋翼動平衡調整分析方法能快速有效地對動平衡值進行調整。
3.2 某型直升機試飛現場試驗
通過在試飛現場對某型直升機(為五片槳葉旋翼系統)的試驗數據分析,檢驗本文所提方法,在直升機真實飛行環境中對旋翼動平衡調整的實際效果。
試驗結果分析,如表2所示。
從表2中可知,兩組試驗,通過加載I次試配重,均能將直升機的旋翼動平衡值調整到使用要求以下。
通過在某型直升機上的試驗結果表明,本文所提直升機旋翼動平衡調整分析方法在直升機真實飛行環境中能有效地降低旋翼的動平衡值。
4 結論
通過兩次試驗結果表明,與常用的直升機旋翼動平衡分析方法相比,本文提出的基于階次跟蹤的直升機旋翼動平衡調整分析方法,采用計算分析方法獲得旋翼的動平衡值,有效克服了傳統頻譜分析方法存在的頻率混疊及能量泄露等問題;旋翼動平衡值的計算及調整建議的計算均通過軟件實現,大大降低了使用成本以及對地勤工作人員的使用要求;同時該方法具有較好的通用性,通過預設的動平衡配置文件,便可實現不同型號不同架次的直升機動平衡調整的需要。
參考文獻
[1]W.約翰遜.直升機理論[M].孫如林,譯.北京:航空工業出版社,1991.
[2]趙小全,湯永,陳功力.基于試重法的直升機旋翼動平衡調整[J].航空維修與工程,2013,(02):79-81.
[3]王強,蔣安民.基于Model 2020的直升機旋冀錐體及動平衡技術研究[J].航空維修與工程,2009,(06):62-64.
[4]張勇,汪興海,孫江.一種手持式直升機旋翼同錐度檢測儀[J].新技術新工藝,2013(11):35-37.
[5]周秋峰.直升機旋冀動平衡優化研究[D].南京:南京航空航天大學,2013.
[6]徐永勤.旋冀動平衡故障診斷方法與試驗系統研究[D].南京:南京航空航天大學,2017.
[7]ERIC B,AUSTIN F,EPHRAHIM G.Rotortrack and balance improvement[C]//Annual Conference of Prognosticsand Heath Management Society 2013.Montreal:American HelicopterSociety,2013:1-9.
[8]張功虎,李玉川,李楊.直-x直升機旋翼動平衡檢查調整方法研究[J].直升機技術,2014,(04):57-59.
[9]宋云雪,李森,陳磊.直升機交互式槳葉振動調整仿真研究[J].計算機測量與控制,2016,24(02):293-296.
[10]高亞東,鄧升平.基于支持向量機的直升機旋翼不平衡故障分類研究[J].南京航空航天大學學報,2011,43(30):435-438.
[11]P BORGHESANI,P PENNACCRI,SCHATTERTON,et al.The velocitysynchronous discrete Fouriertransform for order tracking in thefield of rotating machinery[J].Mechanical Systems and Signal Processing.2014,44(1-2):118-133.
[12]戴功偉.基于自適應轉頻跟蹤濾波的旋轉機械階次分析研究[D].重慶:重慶大學,2013.
[13]PAN M C,CHU W C,D D LE.Adaptiveangular-velocity Vold-Kalmanfilter order track ing-Theoreticalbasis numerical implementationand parameter investigation[J].Mechanical Systems and SignalProcessing,2016,81:148-161.
[14]WANG Y,XU G,LUO A.An onlinetacholess order tracking techniquebased on generalized demodulation forrolling bearing fault detection(J].Journal of Sound and Vibration.2016,367(2016):233-249.
[15]GUO Z X,WONG W K,GUO C.A cloud-based intelligent decision一making system for order trackingand allocation in apparelmanufacturing[J].InternationalJournal of Production Research2014,52(04):1100-1115.

