基于測試數據的雷達導引頭技術狀態評估

許漢威，徐廷學，王 銳

（1.海軍航空大學，山東煙臺264001；2.陸軍研究院工程設計研究所，北京100042）

對雷達導引頭的技術狀態評估與監測是維護和保證導彈作戰性能的一項重要工作。技術狀態是反應裝備實時質量狀況的重要指標[1]。目前，對某型導彈的技術狀態檢測多使用定期檢測方式，并在導彈投入演習或實驗前進行綜合檢測。這種檢測方式可以有效檢測某型導彈的技術狀態，但是頻繁的通電測試會降低導彈的使用壽命。同時，對導彈的貯存環境條件產生影響。隨著戰場信息化，戰爭對于武器裝備也提出了更高的要求，傳統的檢測方式已經無法滿足現代戰場對于裝備性能進行有效評估的要求。

隨著狀態評估這一理論的提出和不斷應用、發展，導彈等裝備同樣可以依靠數學方法對各方面采集到的信息進行處理，進而評估裝備技術狀態。通過專家經驗或專家打分來判斷裝備的技術狀態是早期技術狀態評估的主要方式，如模糊綜合評價法[2]、層次分析法[3-4]和D-S證據理論（Dempster-Shafer Theory）[5-7]等。這類評估方式很大程度上會受到專家主觀因素的影響，評估有效性不能保障；同時，這種評估方式對于裝備技術狀態的評估往往只能劃分為2個結果等級，即正常和故障。此外，隱Markov模型法[8]、貝葉斯網絡模型[9-10]和人工神經網絡[11]等也在裝備技術狀態評估中取得廣泛應用，此類研究可以科學地推理裝備技術狀態水平的計算過程，但通常需要較大的訓練樣本才能保障技術狀態評估的準確性。因此，較多新研究對以上方法進行了改進，如張耀輝[12]等人使用自適應神經-模糊推理系統對裝備技術狀態進行非線性擬合，提高了狀態評估精度。逯程[13]等人使用云物元模型克服并適應裝備狀態評估數據的隨機性得到具有對比性的評估結果。在D-S證據理論的基礎上，Shafer[14]開拓性地運用“信度函數”重新闡述了“上、下限概率”，并提出了“證據的數學理論”，也就是證據推理（Evidential Reasoning，ER）算法。安進[15]等則在此基礎上繼續提出一種改進ER方法的裝備質量狀態評估方法，該方法能夠有效降低測試數據的沖突和不確定性。綜上所述，現有關于裝備技術狀態評估的研究已經取得了較大進展，不同的方法具有不同的適應性。但是針對導彈雷達導引頭技術狀態評估的專項研究較少，在裝備技術評估精度上仍然有待改進。

因此，針對傳統檢測方式的缺陷和現有研究不足，本文基于測試數據針對某型導彈雷達導引頭技術狀態進行評估研究。首先，對測試數據進行歸一化和時間修正，基于三角模糊數進行隸屬度與可信度計算；然后，基于改進ER方法設計某型導彈雷達導引頭技術狀態評估算法；最后，利用測試數據進行實例分析，驗證本文算法在雷達導引頭技術狀態評估中的可行性和有效性。

1 雷達導引頭測試數據處理

基于測試數據的裝備技術狀態評估方法對測試數據的可用性和數據對結果的貢獻度要求較高，因此本文首先對雷達導引頭的測試數據進行處理，包括測試參數的歸一化、基于類似可靠度變化函數的時間修正和基于三角模糊數的隸屬度與可信度計算。

1.1 測試參數歸一化

首先，本文對某型導彈雷達導引頭的線路中的10項主要測試數據進行研究，記為參數e1、e2、e3、e4、e5、e6、e7、e8、e9、e10。

為了統一以上測試參數的量綱，便于數據處理，本文首先對各參數進行歸一化處理。

1）計算本次測試數據與上次非故障測試數據的差值δL、本次測試數據與歷史非故障測試數據平均值差值δS、本次測試數據與標準測試數據的差值δB，如式（1）所示。

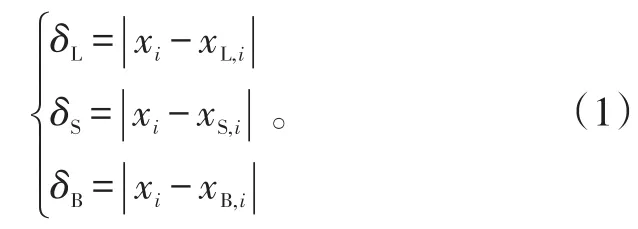
2）分別計算3種歸一方式的量化值λL、λS、λB，如式（2）～（4）所示。

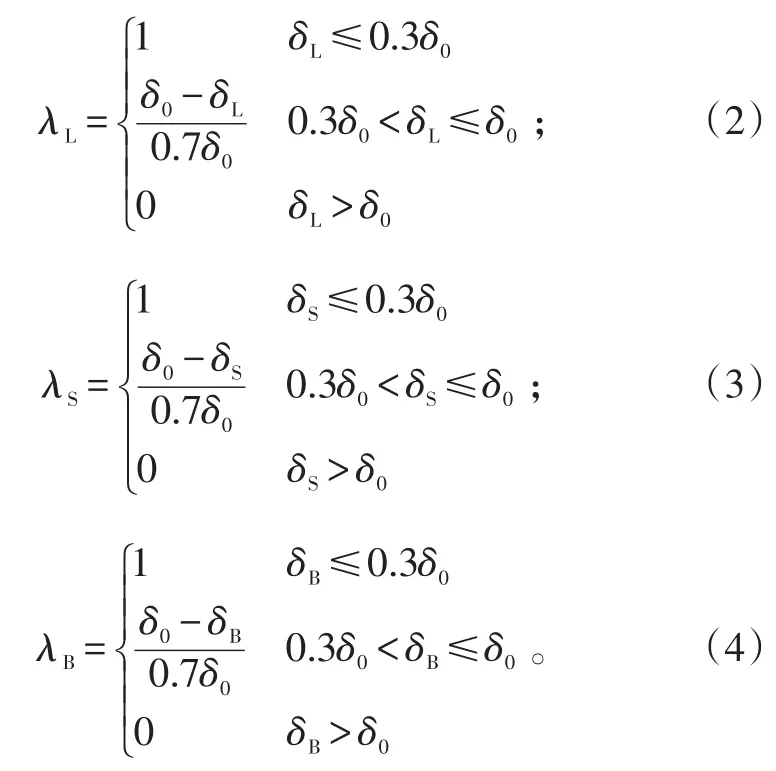
3）計算歸一量化結果，如式（5）所示。

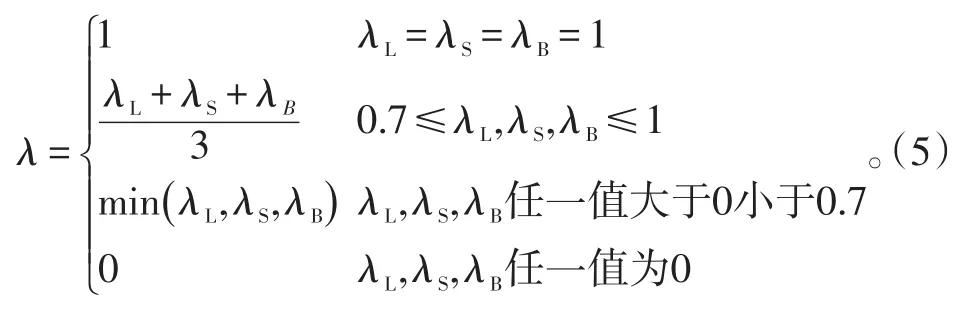
1.2 基于類似可靠度變化函數的時間修正

對于“長期貯存”型裝備，如導彈及其雷達導引頭，其在技術狀態評估之后的很長一段時間內的技術狀態評估值都會被認定為檢測時的結果。如圖1所示，雷達引導頭的技術狀態評估過程和技術狀態的發展即符合這種規律。因此，為了更加準確地表達雷達導引頭當前時間的技術狀態，本文引入時間修正[6]方法，來評估裝備在檢測后一段時間內的技術狀態。裝備的技術狀態失效類型包括應力失效和耗損型失效兩種。耗損型失效是指受到周邊環境的影響，隨著時間的推移導致裝備技術狀態降低的情況，而時間修正即是對耗損型失效問題的處理。

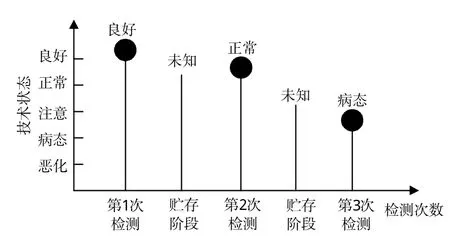
圖1 雷達導引頭技術狀態發展示意圖Fig.1 Development diagram of radar seekers technical status

一般裝備的退化性質滿足“先慢后快”的變化特性，即在很短一段時間內裝備的技術狀態基本呈現不變態勢，隨后呈現緩慢衰減態勢，最后呈現快速衰減態勢。時間轉折點基本為(0 ,T1)、(T1,T2)、(T2,T3)。為了精確描述雷達導引頭技術狀態隨時間退化的狀態，本文建立了類似可靠度變化函數，其隨時間變化曲線如圖2所示。

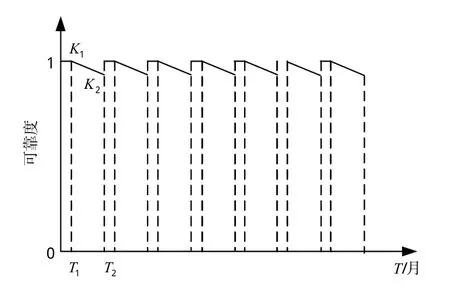
圖2 時間修正函數圖Fig.2 Time correction function

(T1,K1)、(T2,K2)的合理值為(2 ,1)、(1 0 ,0.6 )[16]，則時間修正計算公式如式（6）所示。當T≥10時，該裝備開始進行第二次狀態評估。

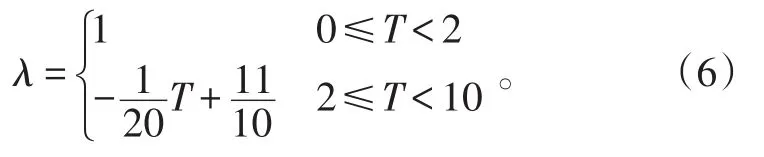
1.3 基于三角模糊數的隸屬度與可信度計算

本文采用三角模糊數群體多屬性決策模型對測試數據結果進行等級劃分[17]。依據文獻[16]，一般將雷達引導頭技術狀態退化情況劃分為病態、惡化、注意、正常、良好5個等級，建立雷達導引頭技術狀態退化三角模糊數模型如圖3所示。5種評估等級下隸屬度的計算如下。

1）良好等級隸屬度計算。

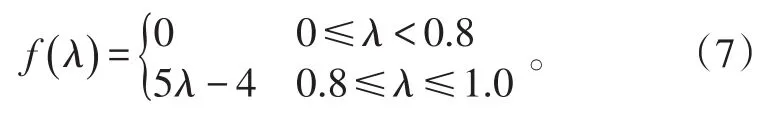
2）正常等級隸屬度計算。

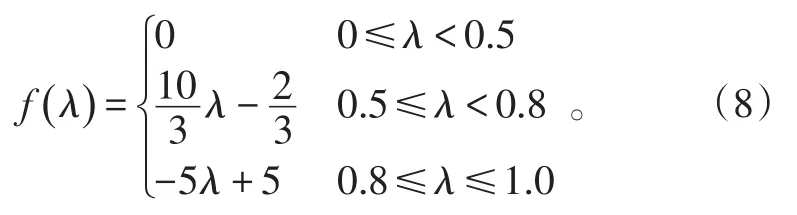
3）注意等級隸屬度計算。

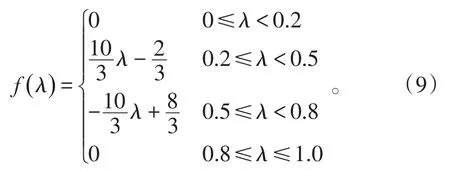
4）惡化等級隸屬度計算。

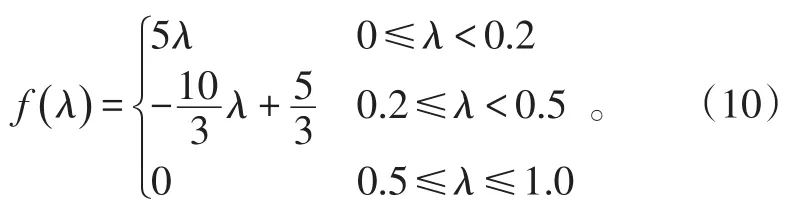
5）病態等級隸屬度計算。

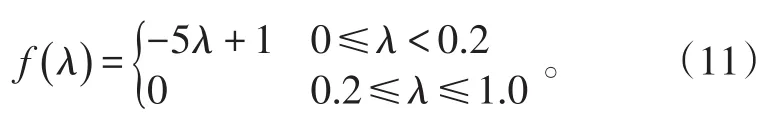
置信度是對測試數據的信任度，通過向專家了解，決定本文取置信度為0.9，則不確定度為0.1，所以根據隸屬度計算可信度。

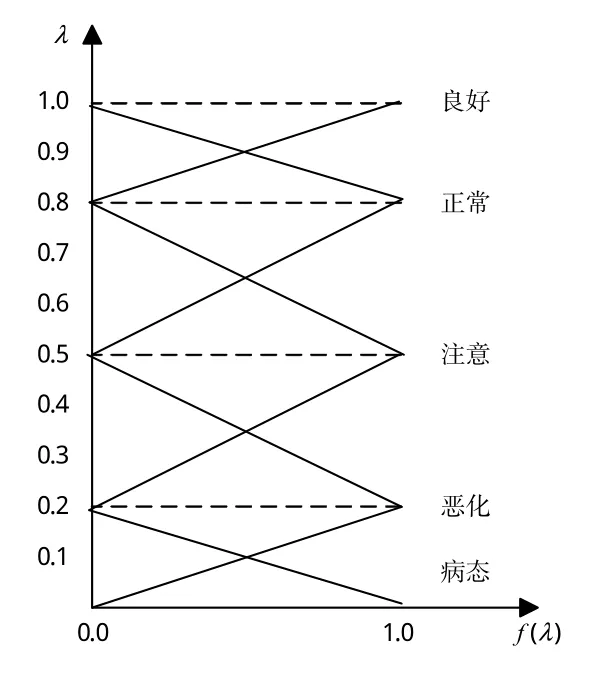
圖3 隸屬度的三角模糊數模型Fig.3 Membership triangle fuzzy number model

2 基于ER算法的雷達導引頭技術狀態評估

ER算法是對D-S證據理論的改進，基于上一節對測試數據的處理，本文進一步使用ER算法對雷達導引頭技術狀態進行評估。

2.1 ER算法設置

1）初始化。定義I個被測參數的集合為E={e1,e2，…,ei,…,eI}，估計I個被測參數的相對權重分別為γ={γ1,γ2,…,γi,…,γI} ，且滿足，；定義L個評估等級H={H1,H2,…,Hl,…,HL}，為了保證一般性，假設Hl+1優于Hl，則對被測參數ei的評估結果可以表示如式（13）所示。

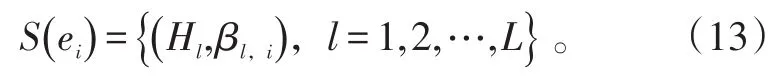
式（13）中，βl,i表示第i個被測參數被評為第l個評估等級的可信度，且滿足。

運用效用理論[18]進行評價結果精確化處理，由于證據理論處理數據得到的結果使用等級來描述，因而很難對評估結果進行進一步比較，故采用效用理論對評估結果進行精確化處理。

2）定義被測參數的概率指派函數。令ml,i表示第i個被測參數ei支持廣義參數F被評為第l個評估等級Hl的程度，為支持概率指派函數；mO,i表示被測參數支持廣義參數F沒有被評為某個評估等級的程度，為不支持概率指派函數。

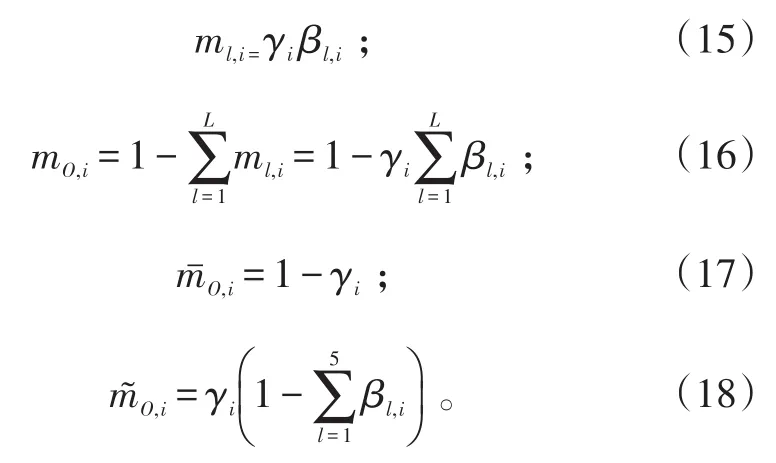
將mO,i分解為，其中是由評估的不完備性引起的不支持概率指派函數分量，表示由于權重而引起的不支持概率指派函數分量。

3）定義廣義參數的組合概率指派函數。令ml,P(i)表示所有I個被測參數支持廣義參數F被評為第l個評估等級Hl的程度；mO,P(i)表示被測參數聚合后，廣義參數F沒有分配給具體評估等級的程度。

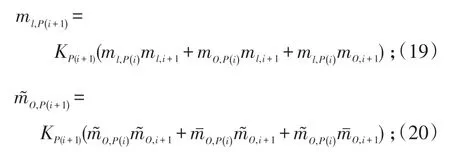
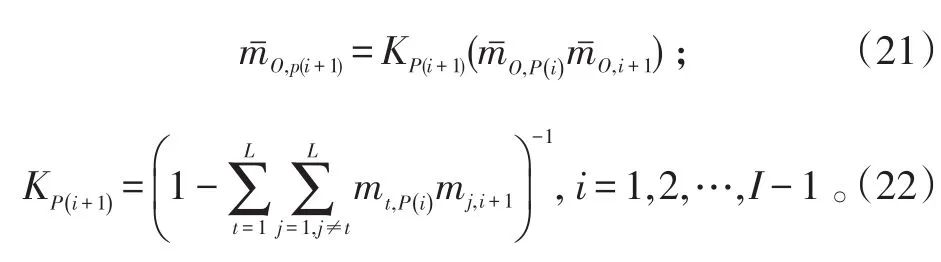
式（19）～（22）中：K為規模化因子，反映了各證據間沖突的程度；P(i+1)表示所有前i+1個基本被測參數。

4）定義廣義參數的組合信任度。聚合所有I個被測參數的估計后，繼續進行標準化處理，得到組合信任度，計算公式為：

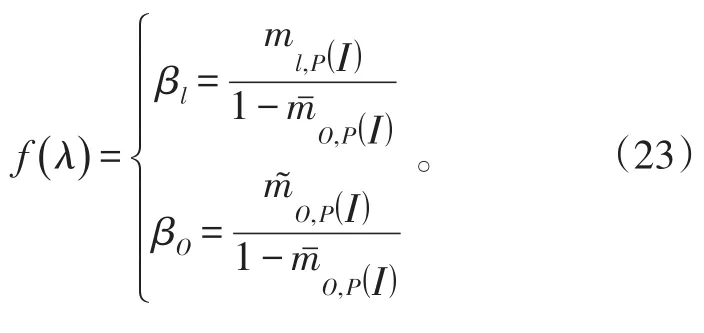
式（23）中：βl表示廣義參數被評為第l個評估等級的可信程度；βO表示未被分配的可信度。

2.2 雷達導引頭技術狀態評估ER算法流程

基于測試數據的處理和雷達導引頭技術狀態評估ER方法，本文的雷達導引頭技術狀態評估改進ER算法流程如圖4所示。

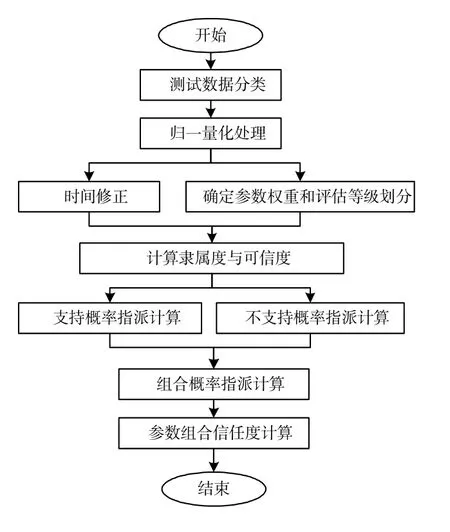
圖4 算法流程Fig.4 Algorithm flow chart

3 實例分析

本文以單位所貯存導彈雷達導引頭的技術狀態評估為例對本文的算法進行驗證。實驗使用Matlab進行計算，使用某單位在某次檢測時得到雷達導引頭測試數據，原始測試數據如表1所示。

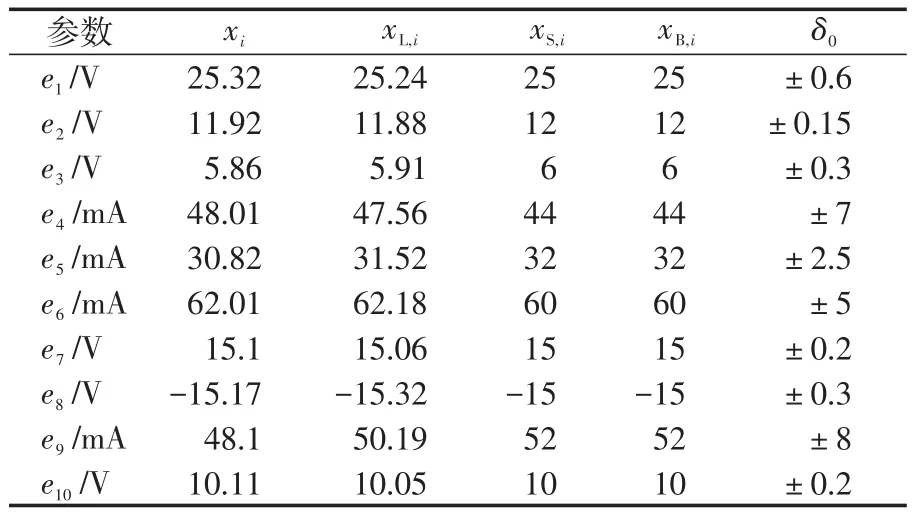
表1 雷達導引頭測試數據表Tab.1 Radar seeker test data

3.1 測試數據處理

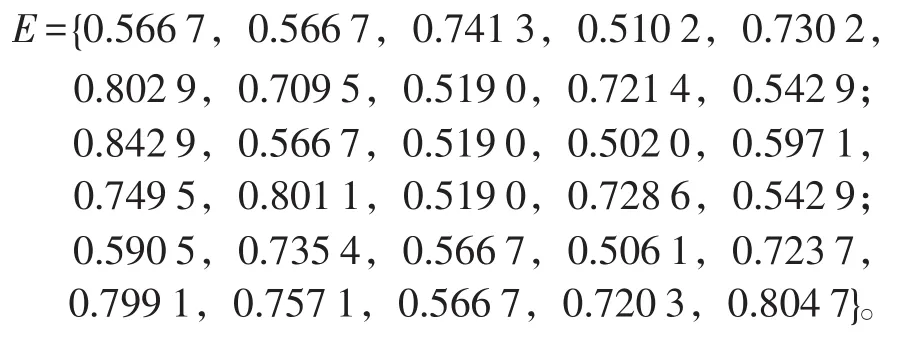
首先，根據式（1）～（4）計算各參數和各標準值之間的偏差值和量化值，進而根據式（5）計算出各參數的歸一量化值為：

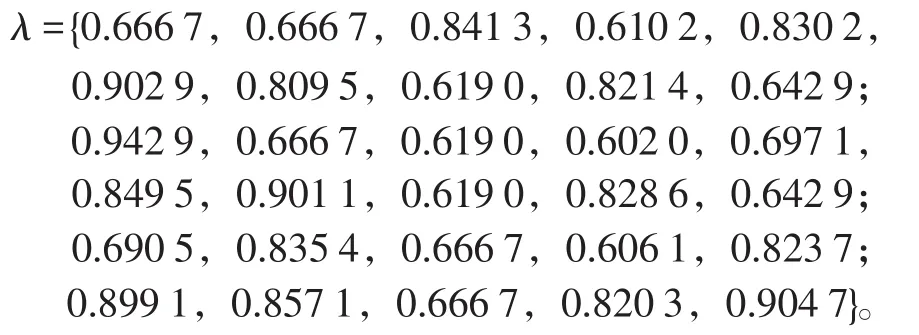
其次，根據式（6）計算時間修正后的歸一量化值為：

然后，根據式（7）～（11）計算出測試數據的10個參數對于不同等級的隸屬度，如表2所示。

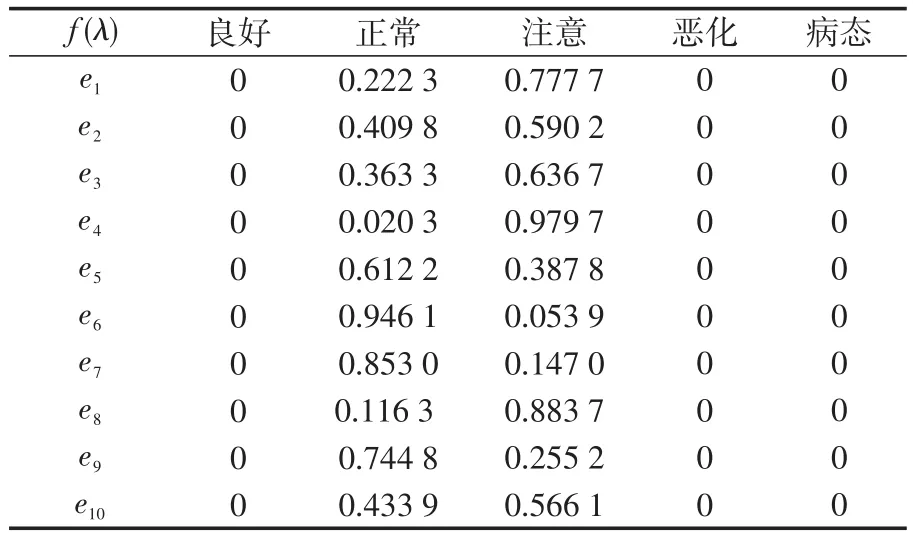
表2 測試數據的隸屬度Tab.2 Membership of test data

得到10個被測參數的隸屬度，取置信度為0.9，根據式（12），計算出各評估等級可信度，如表3所示。

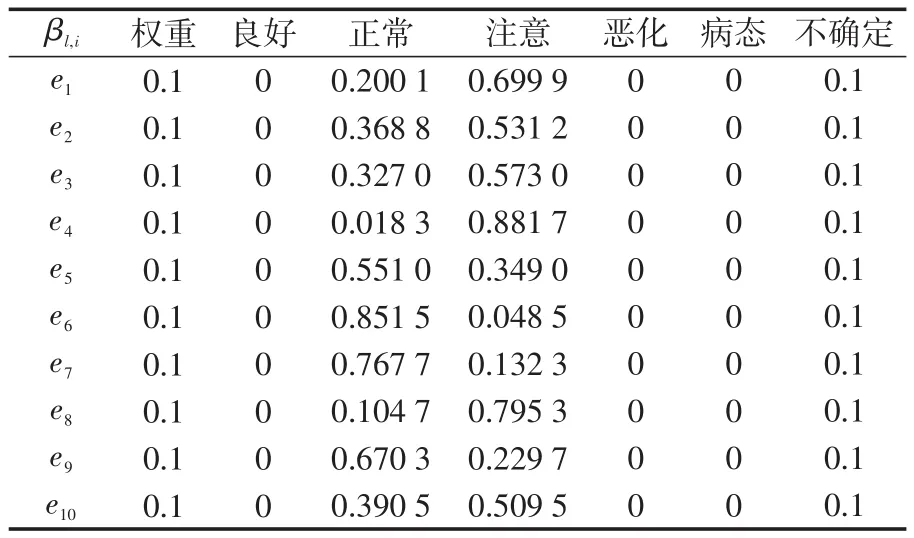
表3 等級可信度分配表Tab.3 Distribution list of grade credibility

分別計算5個被測參數支持廣義參數某獎項質量被評為5個等級中某個等級的程度，即概率指派函數，根據式（15）計算，結果如表4所示。

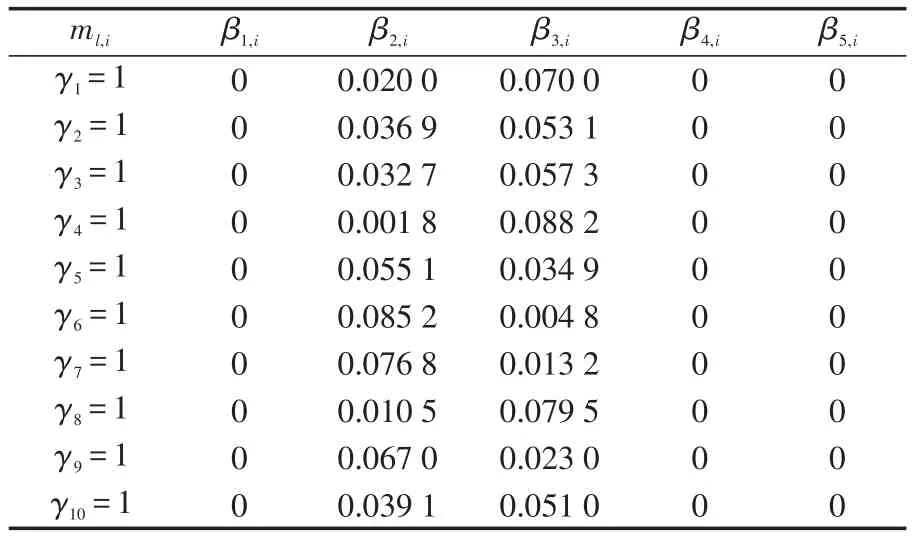
表4 概率指派函數表Tab.4 Function table of probability assignment

3.2 基于ER算法的技術狀態評估

由支持概率指派函數求得結果，根據公式，計算不支持概率指派函數如下：當i=1時，；。

同理，當i=2,3,4,…,10時，計算不支持不支持概率指派函數如下：。

根據規模化因子求解公式計算規模化因子

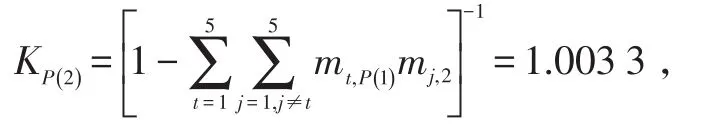
同理，計算規模化因子KP(3)=1.006 3；

計算規模化因子KP(4)=1.007 1；

計算規模化因子KP(5)=1.012 5；

計算規模化因子KP(6)=1.017 6；

計算規模化因子KP(7)=1.016 9；

計算規模化因子KP(8)=1.020 2；

計算規模化因子KP(9)=1.020 6；

計算規模化因子KP(10)=1.022 7；

根據組合信任度公式求解組合信任度：β1=0；β2=0.442 1；β3=0.426 2；β4=0；β5=0；βO=0.076 4。

所以，數據合成后的計算結果為（0，0.442 1，0.426 2，0，0），不確定度為0.076 4。可以將評定結果確定為正常的概率為44.21%；可以將評定結果確定為注意的概率為42.62%。綜合上述結果，該雷達導引頭的技術狀態評估等級為正常。

3.3 基于技術狀態預測的雷達導引頭檢測規劃

通過引入基于時間修正的改進ER算法，可以實現雷達導引頭的狀態監測，使維修方式向基于狀態維修轉變，適應現代戰場需求，提高導彈綜合作戰能力。

實際使用中，對于某雷達導引頭的技術狀態監測周期為半年，在需要進行演習或戰備任務時，需要進行額外測試。基于時間修正的改進ER算法可以在一次測試之后根據裝備退化規律，推算雷達導引頭的技術狀態發展情況，檢測周期更加靈活，避免了傳統檢測方法中“檢測過剩”和“檢測不足”的問題。

4 結論

為實現雷達引導頭的技術狀態監控，本文基于測試數據對某型雷達導引頭技術狀態進行評估。引入時間修正方法，實現了雷達導引頭技術狀態的實時評估，最大限度發揮作戰效能。使用ER算法設計了基于測試數據的雷達導引頭技術狀態評估算法，得到信息的信任度，實現了檢測次數的合理控制，使維修方式向基于狀態的維修方法轉變。本文研究結果有利于提升維護人員的工作效率，保障雷達導引頭的使用壽命與綜合作戰性能。