永磁電動機結構參數對齒槽轉矩的影響綜述

林傳霖 林 珍

（福州大學電氣工程與自動化學院，福州 350116）

永磁電動機是有別于傳統電勵磁電動機的新型電動機，與電勵磁電動機相比具有結構簡單可靠、體積小損耗低等特點。我國稀土資源豐富加上高性能永磁材料的發展，永磁電動機的研究對我國具有重要的戰略意義。

齒槽轉矩是永磁電動機特有的問題，在永磁體和定子或轉子槽之間發生相對位移時產生。齒槽轉矩過大的危害主要有兩點：①會引起電動機的振動進而影響對電動機的控制精度；②產生噪聲，影響用戶體驗，因此關于齒槽轉矩的產生機理、計算方法和削弱措施一直是中外學者的研究熱點。而對電動機性能改善的研究方法，主要通過控制策略的改進和對電動機結構參數的優化。本文將從電動機本體設計的角度出發，對國內外齒槽轉矩的削弱研究進行綜述[1-3]。

目前對于齒槽轉矩的分析計算方法一般為解析法和有限元法。為了兼顧準確性與計算時間，采用解析法和有限元法結合對齒槽轉矩進行研究分析。這也是目前研究齒槽轉矩中普遍使用的方法[4-10]。

1 齒槽轉矩的解析分析

齒槽轉矩的定義是電動機不通電時的磁場能量W對定轉子相對位置角α 的負導數[2]，即

式中，α為齒中心線與相應的永磁磁極中心線之間的夾角。

假設鐵心的磁導率無窮大，電動機內的磁場能量可近似為永磁體與氣隙內磁場能量之和，即

氣隙磁密沿電樞表面的分布可近似表示為

式中，r()Bθ為永磁體剩磁；(,)δθα為有效氣隙長度；m()hθ為永磁體充磁方向長度沿圓周方向的分布。這樣式（2）可以表達為

式中，αp為永磁磁極的極弧系數；Br為永磁體剩磁；p為極對數。

在區間[?π/z, π/z]上對其進行傅里葉展開，當α =0時，即永磁體磁極與相應齒的中心位置重合，則展開式為

α≠0時，即永磁體磁極與相應齒的中心位置錯開，展開式為

式中，z為定子槽數。

3）齒槽轉矩表達式

不考慮斜槽時，當mn≠時，三角函數在[0, 2π]內的積分滿足

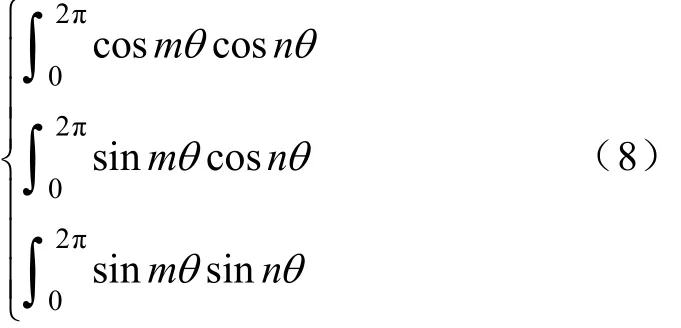
將式（4）、式（5）和式（7）代入到式（1），結合式（8）得到

式中，A=πzLs/4μ0；Ls為電樞鐵心的軸向長度；R= R2?R2；R1為電樞外半徑；R2為定子軛內半徑；2 1n是使nz/2p為整數的整數。

考慮斜槽時，齒槽轉矩表達式為

式中，X=Nsθs；Ns為電樞所斜槽數；θs為用弧度表示的電樞齒。

2 齒槽轉矩的削弱方法

2.1 極弧系數的選擇對齒槽轉矩的削弱

1）當極弧系數惟一時

通過對齒槽轉矩的解析分析，由式（5）可以得出極弧系數αp的選擇對齒槽轉矩有一定的影響，文獻[11]以一臺 6極實心轉子永磁同步電動機為例進行分析，分別討論定子為36槽和48槽時，齒槽轉矩分別與(θ)的6K和8K次（K為整數）傅里葉分解系數有關，并用有限元法進行驗證。以定子為36槽時為例，結果如圖1所示。

圖1 z=36時，Brn隨極弧系數的變化曲線

極弧系數分別取0.8333和0.75時的齒槽轉矩，由圖2可以看出，選取極弧系數為0.8333時，齒槽轉矩較極弧系數為0.75時有較大幅度的減小。

圖2 z=36時，不同極弧系數時齒槽轉矩

可以得出αp作為齒槽轉矩θ)的傅里葉分解后所得式子中的系數，通過合理選擇，可以盡可能地削弱齒槽轉矩。但需要注意的是，(θ)傅里葉分解后的系數中只有nz/2p次與齒槽轉矩有關。

2）當極弧系數不惟一時

文獻[7, 12]采用極弧系數的組合對齒槽轉矩進行削弱。組合極弧系數就是相鄰磁極的極弧系數不相等，通過對其進行優化組合來達到削弱齒槽轉矩的目的。使用這種方法電動機的極弧系數就不是惟一的。文獻[12]引入全局優化方法（zooming algorithm）和有限元法相結合對弧系數組合進行計算得到最優方案。以一臺6極30槽的樣機為例，進行優化，通過解析分析可知當相鄰磁極極弧系數優化組合為αp1=0.8, αp2=0.6再通過算法對αp1, αp2附近的可行域進行優化，尋找到最優組合。對比結果，如圖3所示。

圖3 不同極弧系數組合時齒槽轉矩比較（z=36）

結果表明，相比于單一極弧系數，相鄰磁極極弧系數組合優化后的齒槽轉矩可顯著減小。這種方法的缺點相比于極弧系數不同時電動機的制造工藝要求較高。

2.2 永磁電動機定子槽各項參數對齒槽轉矩的削弱

1）槽口寬度對齒槽轉矩的削弱

槽口的寬度是電動機設計過程中的一個重要的參數，文獻[13-15]通過研究，提出了可以通過使電樞槽不均勻分布的方法來削弱齒槽轉矩。通過改變氣隙之間的磁導，使式（6）或式（7）中的系數Gn減小，從而達到削弱齒槽轉矩的目的。但是采用不均勻的結構會影響電動機對稱性。

文獻[16]基于上述原理，在不破壞電動機的對稱性的情況下，統一槽口寬度變化尺寸，通過有限元法計算，得出不同槽口寬度與齒距的比值V所對應的齒槽轉矩，如圖4所示。

結果表明，隨著槽口寬度的變化齒槽轉矩幅值也有相應的變化，選擇適當的V值可以起到明顯削齒槽轉矩的效果。這種方法在實際的制作工藝上比較容易實現。

圖4 不同槽口寬度齒槽轉矩的對比

2）槽口偏移對齒槽轉矩的削弱

電動機總齒槽轉矩波形可由每個槽產生的齒槽轉矩疊加而成[15,17-18]，基于這個結論，進行槽口偏移對齒槽轉矩影響的分析研究時，總的齒槽轉矩可以看做單個或一個單元組的齒槽轉矩，在偏移角度內的疊加。文獻[19]給出了偏移角度的分組和計算方法，通過偏移槽口，其他結構保持不變，可以消除特定次數的齒槽轉矩諧波。槽口均勻分布和槽口偏移方法時產生的齒槽轉矩對比波形如圖5所示。

圖5 電動機齒槽轉矩對比

可以看出經過槽口偏移處理后，齒槽轉矩幅值降低。從制作工藝的角度出發這種方法比較容易實現，但是也有其局限性，不適用于槽寬小于槽口計算偏移角度的電動機，適用于M=z2p/Ns＞1的電動機。Ns為電動機旋轉一周齒槽轉矩的波動周期數。

3）斜槽、分數槽、虛擬槽對齒槽轉矩的削弱

定子斜槽或轉子斜極是削弱永磁電動機齒槽轉矩常用的方法。通過斜槽可以抑制電樞繞組中空載反電動勢的高次諧波，空載反電動勢的幅值下降。當高次諧波得到抑制時，齒槽轉矩的也得到了削弱。通常斜一個槽的時候齒槽轉矩的削弱效果最好。缺點是不能削弱永磁體端部和鐵心端部之間的磁場產生的齒槽轉矩，當電動機鐵心較短或者槽數很少時，斜槽和斜極實現起來都比較困難[20-21]。

分數槽繞組對齒槽轉矩的抑制有比較好的效果。每極每相槽數q=z/2pm，q不是整數的時候，磁極與齒槽之間的相互作用頻率增加，使得所產生的齒槽轉矩幅值降低。

虛擬槽就是在定子上開輔助槽，槽的寬度與定子槽寬度一致，深淺要合適，可以通過有限元法計算選擇。對齒槽轉矩的影響相當于增加了定子槽數，齒槽轉矩的頻率增加而幅值相應減小[22-23]，這點與分數槽繞組方法的原理相同。

2.3 磁極參數優化對齒槽轉矩的削弱

1）永磁磁極的分塊對齒槽轉矩的削弱

永磁磁極分塊對齒槽轉矩的削弱也可以利用齒槽轉矩的疊加結論進行研究。文獻[24]把每個永磁磁極分為寬度相同的N塊，均勻分布，每個分塊的寬度為θ，相鄰分塊的間隔為γ。單個永磁分塊產生的齒槽轉矩表達式為

式中，Δβ =γ +θ，為相鄰兩塊永磁分塊的偏移角度。通過合理選擇偏移角度Δβ，令 sin (n Npz(α +( m ?1)Δ β))，消去齒槽轉矩的n次諧波。

這種方式有一定的局限性，對于內置切向式永磁電動機的作用不明顯，且當N=2時，雖然基波和奇次諧波得到了很好的抑制，但是2次諧波變為原來的2倍，齒槽轉矩的幅值并沒有削弱。

2）磁極偏移對齒槽轉矩的削弱

與槽口偏移法相對應的是磁極偏移法。這種方法的研究受到了人們的關注，文獻[7, 8, 20, 25]通過磁極偏移減小永磁體對稱時已經存在的齒槽轉矩諧波，但是沒有考慮由于磁極偏移而產生新的諧波。文獻[26]提出的磁極偏移角度計算方法得到的偏轉角度對原有齒槽轉矩諧波以及新引入的低次諧波都有較好的削弱作用。對傳統的磁極偏移方法進行了優化。

3）磁極不對稱對齒槽轉矩的削弱

根據永磁體的擺放位置的不同，永磁電動機可以分為表貼式和內置式永磁電動機。文獻[20]研究了永磁體不對稱對表面式永磁電動機齒槽轉矩的影響。文獻[27]對內置式永磁無刷電動機進行了研究。文章對該電動機磁極不對稱時齒槽轉矩進行解析分析，得到齒槽轉矩的表達式。當磁極不對稱時，若電動機極數為 2p，就會有 2p個與磁極對稱時中心線相對偏移的角度解[27-28]。考慮到由于磁極的不對稱會產生新的諧波，文獻[27]將有限元法和全局優化法相結合，對2p個角度在約束條件內進行尋優，找到最適合的一組解，削弱齒槽轉矩。

磁極不對稱的方法對齒槽轉矩削弱效果良好。但由于永磁體偏移的角度各不相同，對電動機制造的工藝要求很高，不太適用于實際電動機生產制造。

2.4 其他方法對齒槽轉矩的削弱

除了上述幾種方法外，針對表貼式永磁電動機還可采用不等厚永磁磁極的方法。這種方法是把用本內外徑同心的永磁體改成內外徑不同心，使永磁體不等厚，來減小式（9）中Brnz/2p，從而削弱齒槽轉矩[29]。針對雙定子永磁同步電動機，文獻[30-31]提出了一種新型的雙定子結構的永磁電動機如圖6所示。

圖6 雙定子永磁同步電動機結構

本文分析了內外定子相對位置變化對齒槽轉矩的影響規律。通過合理選擇內外定子相對位置，可以有效削弱齒槽轉矩。

轉子結構也會對齒槽轉矩產生影響。傳統電動機轉子與定子間的氣隙是均勻的，通過改變轉子的表面結構，在相鄰的兩對極之間適當弧度的凹陷，得到不均勻的氣隙，改善氣隙磁路，從而達到削弱齒槽轉矩的目的。

3 結論

本文主要從永磁電動機的極弧系數、電樞槽結構參數、磁極結構參數3個部分，總結了國內外對齒槽轉矩這一永磁電動機特有的問題的研究現狀。齒槽轉矩在實際情況中比較難以測量，對它的研究主要是通過解析法與有限元計算綜合分析驗證。齒槽轉矩作為永磁電動機特有的一個問題，今后還會有學者對其進行研究，隨著研究的深入和制作工藝的提升，除了對電動機控制策略的研究之外，還對電動機的多個結構參數進行組合優化來削弱齒槽轉矩會達到更好的效果。在討論多組結構參數對齒槽轉矩的影響時，需要引進相應的數學算法與有限元法相結合，再進行優化。

[1] 唐任遠. 現代永磁電機理論與設計[M]. 北京: 機械工業出版社, 2016.

[2] 王秀和. 永磁電機[M]. 北京: 中國電力出版社,2007.

[3] 蔡長銘, 湯寧平. 低速永磁同步電機的齒槽轉矩分析[J]. 防爆電機, 2008, 43(1): 5-8.

[4] 安忠良, 李國麗, 周挺. 內置式永磁發電機隔磁磁橋形狀對齒槽轉矩的影響[J]. 電氣技術, 2014, 15(4):1-4, 19.

[5] Ko H S, Kim K J. Characterization of noise and vibration sources in interior permanent-magnet brushless DC motors[J]. IEEE Transactions on Magnetics, 2004, 40(6): 3482-3489.

[6] 楊玉波, 王秀和. 永磁體不對稱放置削弱內置式永磁同步電動機齒槽轉矩[J]. 電機與控制學報, 2010,14(12): 58-62.

[7] Bianchi N, Bolognani S. Design techniques for reducing the cogging torque in surface-mounted PM motors[C]//IAS 2000-Conference Record of the 2000 IEEE Industry Applications Conference, VOLS 1-5, 1,2000: 179-185.

[8] Breton C, Bartolome J, Benito J A, et al. Influence of machine symmetry on reduction of cogging torque in permanent-magnet brushless motors[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3819-3823.

[9] 郝立, 林明耀, 徐妲, 等. 軸向磁場磁通切換型永磁電機齒槽轉矩抑制[J]. 電工技術學報, 2015, 30(2):21-26.

[10] 蘇強, 王開芝, 高星福. 鑄鋁轉子端環開槽改善電機起動性能的分析[J]. 電機技術, 2017(2): 9-12.

[11] 王秀和, 楊玉波, 丁婷婷, 等. 基于極弧系數選擇的實心轉子永磁同步電動機齒槽轉矩削弱方法研究[J].中國電機工程學報, 2005, 25(15): 146-149.

[12] 楊玉波, 王秀和, 丁婷婷, 等. 極弧系數組合優化的永磁電機齒槽轉矩削弱方法[J]. 中國電機工程學報,2007, 27(6): 7-11.

[13] Zhu Z Q, Ruangsinchaiwanich S, Ishak D, et al.Analysis of cogging torque in brushless machines having nonuniformly distributed stator slots and stepped rotor magnets[J]. IEEE Transactions on Magnetics, 2005, 41(10): 3910-3912.

[14] Kim T H, Won S H, Bong K, et al. Reduction of cogging torque in flux-reversal machine by rotor teeth pairing[J]. IEEE Transactions on Magnetics, 2005,41(10): 3964-3966.

[15] Wang Daohan, Wang Xiuhe, Qiao Dongwei, et al.Reducing cogging torque in Surface-Mounted Permanent-Magnet motors by nonuniformly distributed teeth method[J]. IEEE Transactions on Magnetics, 2011,47(9): 2231-2239.

[16] 楊玉波, 王秀和, 朱常青. 電樞槽口寬度對內置式永磁同步電機齒槽轉矩的影響[J]. 電機與控制學報,2011, 15(7): 21-25.

[17] 劉婷, 歐陽紅林, 黃守道. 基于重復單元削弱永磁風力發電機齒槽轉矩[J]. 電工技術學報, 2011,26(12): 43-48.

[18] Zhu Z Q, Ruangsinchaiwanich S, Howe D. Synthesis of cogging-torque waveform from analysis of a single stator slot[J]. IEEE Transactions on Industry Applications, 2006, 42(3): 650-657.

[19] 黃守道, 劉婷, 歐陽紅林, 等. 基于槽口偏移的永磁電機齒槽轉矩削弱方法[J]. 電工技術學報, 2013,28(3): 99-106.

[20] Ishikawa T, Slemon G R. A method of reducing ripple torque in permanent magnet motors without skewing[J]. Magnetics, IEEE Transactions on, 1993,29(2): 2028-2031.

[21] Zhu Z Q, Howe D. Influence of design parameters on cogging torque in permanent magnet machines[C]//Electric Machines and Drives Conference Record,2002: 3.

[22] 唐旭, 王秀和, 田蒙蒙, 等. 基于改變定子齒槽參數的異步起動永磁同步電動機齒槽轉矩削弱措施研究[J]. 電工技術學報, 2016, 31(23): 1-8.

[23] 劉偉, 陳麗香, 唐任遠. 定子齒頂開輔助槽削弱永磁電機齒槽轉矩的方法[J]. 電氣技術, 2009, 10(8):51-53.

[24] 楊玉波, 王秀和, 朱常青. 基于分塊永磁磁極的永磁電機齒槽轉矩削弱方法[J]. 電工技術學報, 2012,27(3): 73-78.

[25] Bianchi N, Bolognani S. Reducing torque ripple in PM synchronous motors by pole-shifting[J]. 2000.

[26] 楊玉波, 王秀和, 張鑫, 等. 磁極偏移削弱永磁電機齒槽轉矩方法[J]. 電工技術學報, 2006, 21(10):22-25, 61.

[27] 王道涵, 王秀和, 丁婷婷, 等. 基于磁極不對稱角度優化的內置式永磁無刷直流電動機齒槽轉矩削弱方法[J]. 中國電機工程學報, 2008, 28(9): 66-70.

[28] 楊玉波, 王秀和. 永磁體不對稱放置削弱內置式永磁同步電動機齒槽轉矩[J]. 電機與控制學報, 2010,14(12): 58-62.

[29] 李偉力, 袁世鵬, 霍菲陽, 等. 磁極不等厚對兆瓦級永磁直驅風力發電機的影響[J]. 大電機技術,2011(4): 30-34, 38.

[30] 劉細平, 黃筱霞. 一種雙定子低速稀土永磁同步風力發電機設計研究[J]. 微電機, 2006, 39(8): 25-27.[31] 劉細平, 林鶴云. 雙定子永磁同步電機齒槽轉矩削弱方法[J]. 東南大學學報(自然科學版), 2007, 37(4):618-622.