三維建模在計算機輔助船舶設計中的兩種思路和應用

趙唯丞， 黃雪忠， 萬雁翔

(1.中國船級社質量認證公司, 北京 100006; 2. 中國船級社江陰辦事處，江蘇 無錫 214422；3. Faculty of Engineering and Environment, Southampton University, Southampton, SO17 1BJ)

0 引 言

建模一直是計算機輔助船舶設計的重要環節。從數學模型到立體三維模型，從桿件模型到船體梁模型，由抽象到形象，由細節到宏觀,無不體現建模思想在計算機輔助設計中的重要性。

三維建模作為現代計算機發展的重要成果之一，廣泛應用于船舶設計的各個階段[1]。三維模型的方便直觀等特性得到了科研人員和設計師們的喜愛。然而，隨著時間推移，三維模型被越來越多地應用于造船業的各個領域[2]，其缺陷也就逐漸暴露出來。比如，在船舶性能計算方面，三維模型的精確性飽受詬病，使得利用三維建模進行的計算只能作為估算結果。而在船舶結構安全的計算方向，雖然有限元模型有效解決很多技術難題，然而有限元模型的建立和邊界條件的確立太過依賴于設計人員個人的工程經驗積累，使得其計算結果精確性和可靠度一度成疑。令人欣慰的是，近年來三維模型在總體設計方向的應用越來越成熟可靠，三維設計的前沿科學家們甚至利用虛擬現實技術(Virtual Reality, VR)開發出軟件來幫助設計師準確把握艙室設計。本文著重介紹三維模型在計算機輔助船舶設計中的反算法。

1 建 模

三維建模是計算機輔助船舶設計的重要步驟，建模的方式、方法會影響計算結果的可靠性，型線的設計可采用計算機輔助三維設計的方法來實現。本文大量采用三維設計，其中涉及Rhino 4軟件和Maxsurf 13軟件的掌握和使用。區別于手工修改型線的方法，本文中三維型線的修改步驟主要經歷以下幾個過程：(1)母型船CAD型線校核；(2)在CAD軟件中通過查詢命令提取型值點三維坐標，并形成固定格式的txt點云文件；(3)將點云文件導入到Rhino軟件中，并使用B-Spline 內插樣條曲線連接各三維坐標形成的點云；(4)利用Rhino軟件的NURS曲面成型模塊，以各樣條線作為約束形成船體NURS曲面；(5)將曲面導入到Maxsurf軟件中并進行參數設置，檢查母型船模型精度；(6)根據之前設計得出的參數，在Maxsurf中執行參數變化命令，形成設計船的模型，并檢查新模型的水動力參數是否符合初步設計的要求；(7)在模型上設置水線、分站、縱剖線等并導出dxf格式的CAD圖紙；(8)在CAD中進行型線的二次光順。

1.1 母型船三維建模

母型船變換法是船舶設計中常見的方法[2]。在母型船的建模過程中，雖然Maxsurf軟件自帶的NURS建模模塊可以完成這部分工作，但依靠錄入型值生成Markers云，再手工拖曳曲面靠近型值點的方法十分耗時且曲面成型精度也有待考證。于是，本文引入第三方NURS曲面成型軟件Rhino，通過在母型船CAD圖中復制出三維坐標的型值制成txt三維坐標文件導入到Rhino軟件中形成型值點云，勾勒各條橫剖線和水線，利用橫剖線和水線約束NURS曲面得到母型船船體外殼。這樣做的好處是曲面精度高，保證各個橫剖面和水線面與型線圖的形狀完全一致。

1.2 逆向建模

逆向建模是指在缺少建模必要條件的情況下進行的船舶三維建模。本文算例中的建模過程由于缺少船舶的半寬水線圖和縱剖線圖，僅有橫剖線圖進行逆向建模。

以下文的反算法算例為例，該驅逐艦(Leander級)建模過程中沒有藍圖或結構，關于其結構的詳細信息也未知，僅有的信息是文獻中的橫剖面插圖[3]。

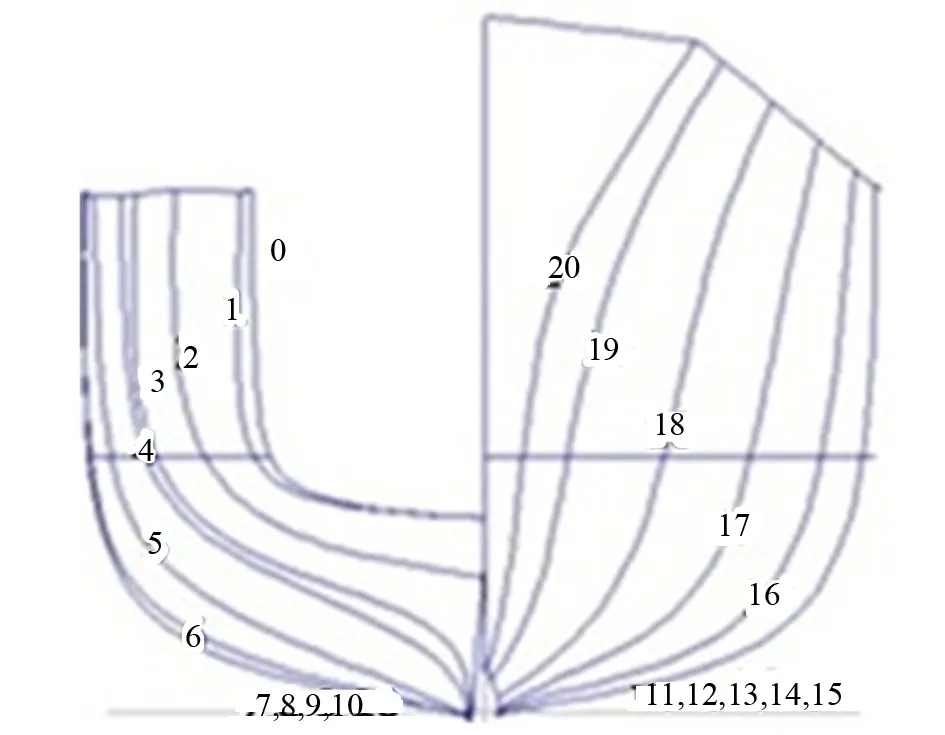
圖1 驅逐艦橫剖面圖

對該驅逐艦進行三維建模，首先須找到其橫截面平面。圖1是在文獻[3]中發表的橫剖面圖。不幸的是，在這個不清晰橫剖面圖上并沒有標明站號或肋位號，因此對站號進行假設，在平面CAD軟件中重新繪制該橫剖面圖。

重新繪制的驅逐艦橫剖面圖如圖2所示，與圖1相比，增加了精確性。通過立體展開橫剖面圖得到3D船體曲線坐標(x,y,z)[4]，如圖3所示。如圖4所示，在得到曲線坐標形成坐標云之后，導入Rhino軟件中得到船體曲面， 再將曲面導入Maxsurf軟件中，進行船體參數和水動力計算模擬。

圖2 驅逐艦橫剖面圖(重新繪制)

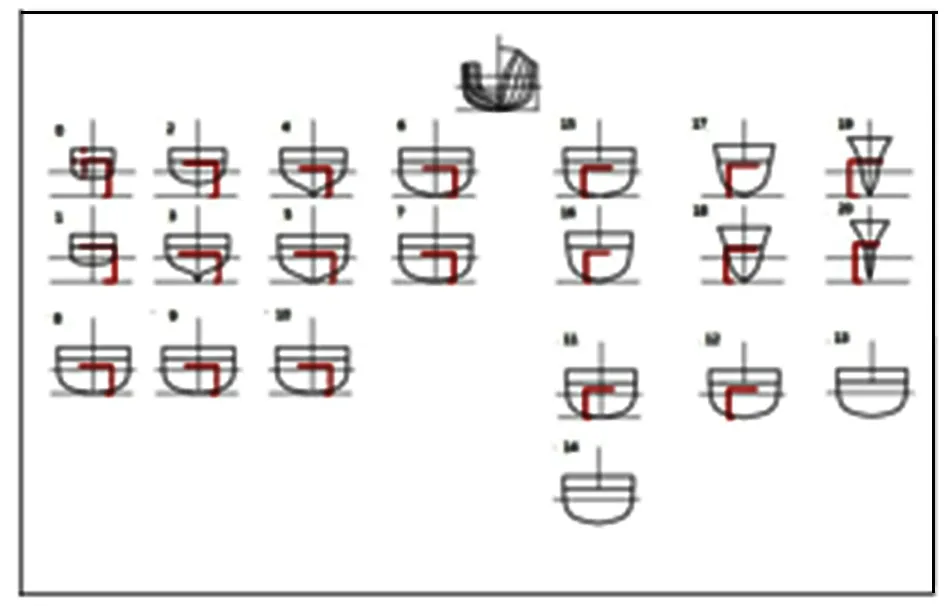
圖3 立體展開的驅逐艦橫剖面圖

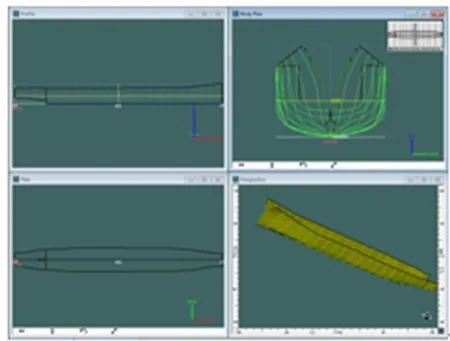
圖4 導入 Maxsurf 后的驅逐艦三維模型

如圖5所示，該模型由于Rhino軟件采用了IGES通用格式可用于在Maxsurf中建立三維模型，也可導入Patran建立有限元模型。

圖5 導入Maxsurf中的3D船體曲面

1.3 有限元模型的建立

如圖6所示，IGES格式的三維船體表面導入到Patran軟件中同樣可以兼容。該表面可用于有限元建模，這樣整個有限元建模的精度可以提高，因為該三維曲面是通過轉化平面CAD藍圖所得到的。

要構建驅逐艦船體的有限元模型，將使用MSC.Patran。這是一種強大的計算軟件，可以構建艦船三維有限元模型。將驅逐艦3D船體表面導入Patran中，其表面長度約為109.72 m，寬度為12.36 m，比例1∶1。在這個表面上畫網格，設計者可以很容易地得到完整的有限元網格結構。

圖7是畫好的驅逐艦模型有限元網格和節點，可以清楚地看到船體表面和甲板上的網狀分布。需要注意的是，兩個表面連接的節點必須是相同的，為了刪除多余的節點，可在Patran中使用等價功能。如果某些節點不相同，會導致計算過程中出現一些問題。

圖7 Patran軟件中驅逐艦模型有限元網格設繪

2 正算法與反算法

2.1 正算法概述

正算法是指用母型船變換法推進的正常設計。該算法具備全部設計要素，通過Maxsurf中的設計模塊轉換母型船三維模型，從而得到新設計船的三維模型，再進行船舶結構、性能等一系列設計。

興波預報是計算機輔助船舶三維設計的重要特色，利用計算機軟件進行興波預報直觀可靠。以船體興波預報作為正算法算例一則，主要是使用Maxsurf 13中的Hullspeed模塊進行船體興波預報工作，預報結果如圖8和圖9所示。

圖8 渲染后的算例中設計船模型興波預告圖

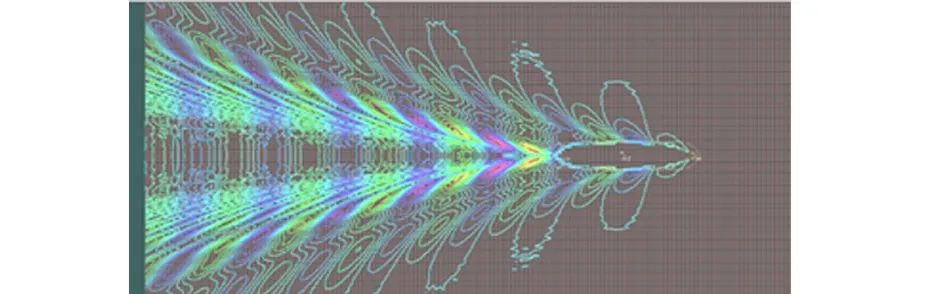
圖9 算例中設計船模型興波波高等高線圖

反算法是指利用計算機輔助設計的方法對缺少圖紙信息的船舶進行反向演算。利用不完整的信息推演出船舶布置或結構的完整信息。

2.2 船體結構逆向設計

第1.2節得到驅逐艦三維船體曲面后，即可對驅逐艦內部結構進行推測，從而推算出驅逐艦船體梁的基本參數。

查閱大量文獻，找到匹配算例中驅逐艦的結構簡圖[5]。圖10顯示一個非常典型的現代驅逐艦橫截面。結構細節顯示，在圖中有2層甲板和立柱。圖10還展示一些骨材梁結構安裝在船體表面,但具體的板架結構是無法假設的，因此，使用一個非常簡化的結構假設。根據前文圖3所示，有21個假設的橫截面平面，在該結構假設中所有的梁和桿結構細節都被忽略了。假定的橫截面僅由主甲板、平臺甲板和船殼組成，忽略立柱抗水平彎曲和扭轉的影響，其原因是很難定義這種效應的大小。該結構假設的關鍵問題是假設板的厚度。

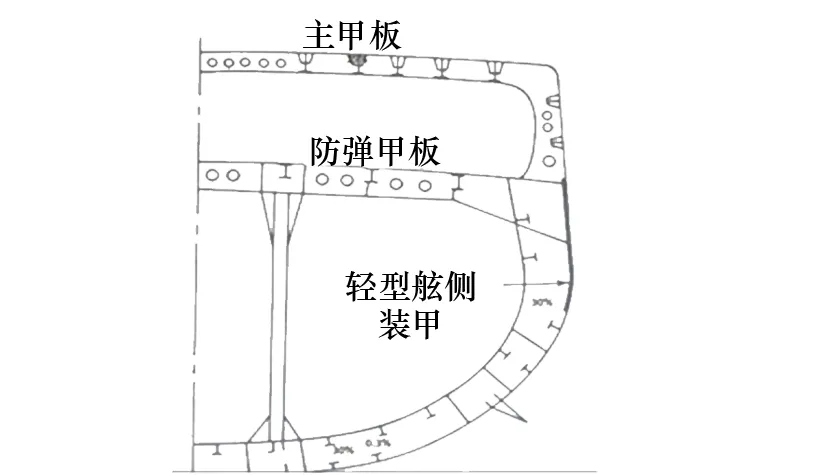
圖10 典型艦船橫剖面圖

為確保有限元模型的質量分布與真實船舶相同，設計人員應假設不同斷面的板厚度。從圖11中可以看出，假設的板厚最大值是10.55 cm，厚度最小值是4.53 cm。這里還有一個重要的假設須注意:截面質量是均勻分布在船體板和甲板上的，在現實中，這是不可能的，因為現實船體中結構的密度并不均勻。

圖11 驅逐艦有限元模型的質量分布

當每個部分的質量假設完成時，設計者可以開始計算縱軸穿過質量中心的轉動慣量。在Patran中有一個質量屬性計算工具，設計者可以用來查詢相對于原點坐標和相對于相對坐標的轉動慣量。從圖12中可以看出，不同部分的網格被設置為組，根據組的設置，可以方便地檢查出每個區段相對于不同軸的轉動慣量。

圖12 計算驅逐艦有限元模型轉動慣量

反算法利用計算機三維建模和有限元軟件在假設條件的情況下可以推算出驅逐艦船體的各類參數，算例中僅例舉了驅逐艦質量分布和慣性矩推算的過程。該算例中所需的面積矩等必需參數同樣可以推算得到。

2.3 在Patran中計算干模態

在Patran中完成三維有限元模型的構建之后，通過Patran軟件將模型導入Nastran就可計算驅逐艦模型的干模態。計算模態是為了驗證反算法中一系列的結構假設是否合理，相似驅逐艦的實船模態計算結果可以從文獻[5]中查找。假設船體梁的兩端都是固定的，并且使用Patran正常模式分析功能，設計師可以得到不同頻次的模態，如圖13所示。

圖13 驅逐艦低頻次干模態

通過利用反算法建立的驅逐艦模型在Patran中計算干模態，設計者會發現船體梁的區域振動會隨著頻率升高而越來越明顯，這是因為反算法假設出的驅逐艦FEA船體模型的內部沒有骨架，該模型只有板。事實上，這在現實中是不會發生的，真實船體中有大量梁和桿結構存在。對比文獻中近似船的垂向彎曲頻率，結果如表1所示。

從表1中可以看出，對比結果誤差太大，前文中敘述了原因。因此，Patran的計算結果并不能給反算法提供滿意的答案。然而，第2.1節從驅逐艦FEA模型中獲得的數據可以導入代碼UCLMOD1進行干模態計算。

表1 Patran計算的垂向彎曲頻率對比文獻中近似船的垂向彎曲頻率

2.4 運用UCLMOD1計算干模態

UCLMOD1是倫敦大學開發的代碼，用來計算船體干模態，用戶只需按格式要求鍵入船體參數就可得到振動頻率和振動波形，使用簡單而直觀。第2.1節計算的很多船體數據可以直接代入UCLMOD1軟件中。由上節可知，FEA并不是反算法中做干模態計算的好工具，設計者可以使用UCLMOD1來計算扭轉和彎曲的振動頻率，從而證明反算法中諸多假設的可靠性。UCLMOD1不需要進行結構細節的輸入，因此從這個代碼的計算結果中得到一個合理的答案可能會容易得多。輸入UCLMOD1需要的驅逐艦結構假設數據，并運行UCLMOD1，設計者可在幾秒鐘內得到結果。圖14為UCLMOD1計算出的當振動頻率為3.909 Hz時驅逐艦的扭轉波形示意圖。

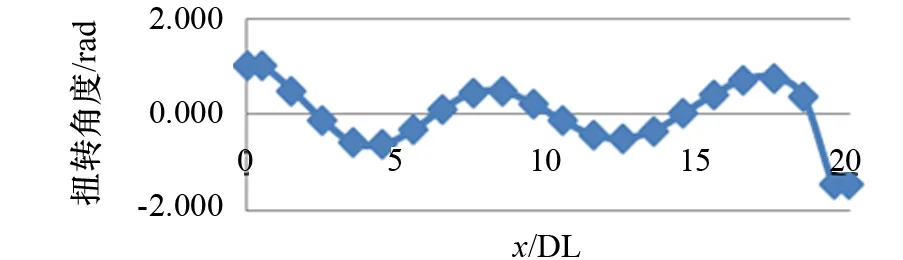
圖14 UCLMOD1計算得到的驅逐艦扭轉波形

2.5 反算法可靠性驗證

振動頻率的計算是由UCLMOD1進行的，為驗證這些頻率，通過文獻[6]，找到1艘該驅逐艦的近似艦船(Canadian)，其主尺度參數與該驅逐艦(Leander)相似。由于船舶類型相似，結構細節可能與該驅逐艦相同。文獻給出了近似艦船的振動頻率。表2中給出UCLMOD1計算出的驅逐艦振動頻率和它的近似艦船的振動頻率，并做橫向比對。

表2 UCLMOD1計算的振動頻率(Leander)與近似艦船(Canadian)振動頻率對比

從表2中可以看出，垂直彎曲誤差不很大，特別是第3階垂直彎曲的誤差可忽略不計。Leander和Canadian驅逐艦的第2階水平彎曲頻率也比較相似。結合垂直彎曲和水平彎曲頻率的對比，設計者可推斷這2艘驅逐艦應具有非常相似的結構特性，并且驗證了第2.1節反算法做出的假設。對比結果說明，由UCLMOD1計算的振動頻率是可靠的，并且第2.1節對該驅逐艦船體結構的假設也是合理的。

3 2種計算方法的比對

從圖15中可以看出，正算法與反算法共同的步驟是三維建模，其余步驟均不相同。同樣為運用三維模型進行計算機輔助船舶設計的方法，反算法步驟與正算法卻大相徑庭，其原因在于這2種計算方法的出發點不同。正算法是正常的計算機輔助船舶設計方法即母型船變換設計，而反算法運用了逆向設計的思維。反算法可運用三維NURBS曲面復原缺少藍圖的船舶外表面，再運用有限元模型為結構假設提供運行代碼所需的參數，在得出假設結構的參數以后，再導入計算代碼得出船舶結構特征數據，比如船體梁的振動頻率等。查找文獻，對比用假設計算出的船舶特征數據和文獻提供的數據誤差，判斷結構假設是否合理。

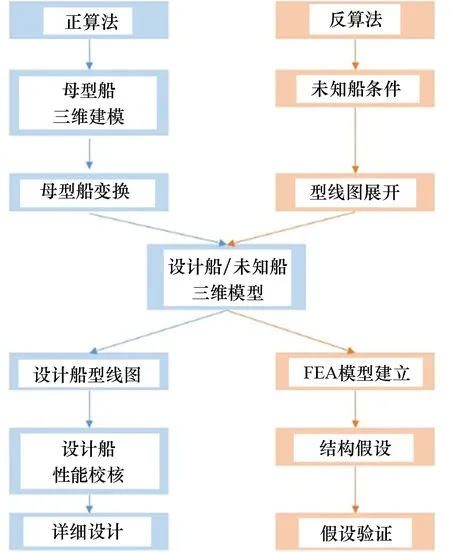
圖15 兩種計算方法的比對

4 結 語

本文敘述三維建模在計算機輔助船舶設計中的2種思路和應用，并指出三維建模在計算機輔助船舶設計中有2種思路。

第1種正算法即常見的運用三維建模軟件推進母型船變換得到設計師需要的新船的方法。該方法目標明確，操作成熟，是目前廣大設計師常用的計算機輔助船舶設計方法之一。隨著計算機性能的飛躍和計算機輔助設計軟件的日趨完善，該方法的應用將越來越廣泛，大到初步設計，小到艙室設計，都有運用正算法思維的計算機輔助船舶設計的身影。

第2種反算法應用于缺少藍圖或其他資料的船舶的復原，是逆向設計思維的一種應用。該方法的利用需復原船舶已有的圖紙資料數據，合理假設，再對假設進行驗證，從而得出需復原船舶缺失的數據。未來的應用前景主要可用于引進海外先進船型填補國內造船業的技術空白，還可用于國防工業。

設計師在運用計算機輔助船舶設計時可以根據設計出發點合理選擇這2種思路建立三維船模，從而做好船舶設計或復原工作。

[1] 顧敏童.船舶設計原理[M].上海：上海交通大學出版社，2006.

[2] 中國船舶工業總公司.船舶設計實用手冊[M].北京：國防工業出版社，1998.

[3] BENNETT S S, HUDSON D A， TEMAREL P.The influence of forward speed on ship motions in abnormal waves: Experimental measurements and numerical predictions[J]. Journal of Fluids & Structures, 2013,39(5):154-172.

[4] 楊永祥，峁文玉，翁士綱.船體制圖[M].哈爾濱：哈爾濱工程大學出版社，2005.

[5] GILLMER T C. Modern Ship Design[R]. Maryland: Naval Institute Press，1977.

[6] MCTAGGART K,DATTA I,STIRLING A,et al.Motions and loads of a hydroelastic frigate model in severe seas[J]. Transactions: The Society of Naval Architects and Marine Engineers，1997, 105:427-450.