空心穩(wěn)定桿的優(yōu)化設計

王偉，王海艷，熊朝恩

（1.一汽技術中心輕型車部底盤設計室，吉林 長春 130011；2.一汽技術中心JC越野車研究所，吉林 長春 130011）

前言

為提高汽車的操作穩(wěn)定性，同時也可以改善汽車的乘坐舒適性，穩(wěn)定桿被廣泛應用于汽車懸架系統(tǒng)。根據(jù)穩(wěn)定桿在實際工作中的受力特點，可將其設計為空心穩(wěn)定桿，獲得30%～45%的降重效果，因此空心穩(wěn)定桿成為目前穩(wěn)定桿領域的研究熱點[1]。本文綜合考慮各種因素，利用能量法給出空心穩(wěn)定桿側傾角剛度、各截面應力計算公式和最大第三強度理論相當應力（以下簡稱相當應力）的橫截面位置，詳細介紹了空心穩(wěn)定桿各設計參數(shù)對其性能的影響。最后在保證空心穩(wěn)定桿設計指標、強度等要求下，以質量最小為目標，以空心穩(wěn)定桿結構及安裝參數(shù)為設計變量，建立其優(yōu)化設計模型，并利用MATLAB軟件完成了對空心穩(wěn)定桿的優(yōu)化設計。

1 空心穩(wěn)定桿設計計算

在多數(shù)汽車上，空心穩(wěn)定桿中部的兩端自由地支承在兩個橡膠套筒內，而套筒則固定在車架上。空心穩(wěn)定桿兩側縱向部分的末端通過支桿與懸架下擺臂上的彈簧支座相連[3]。在非獨立懸架系統(tǒng)中，也有將空心穩(wěn)定桿中部通過吊臂總成與車架相連，縱向部分的末端通過固定支架與車橋相連。某實際輕型商用車前懸架的空心穩(wěn)定桿系統(tǒng)就采用了這種連接方式，如圖1所示。

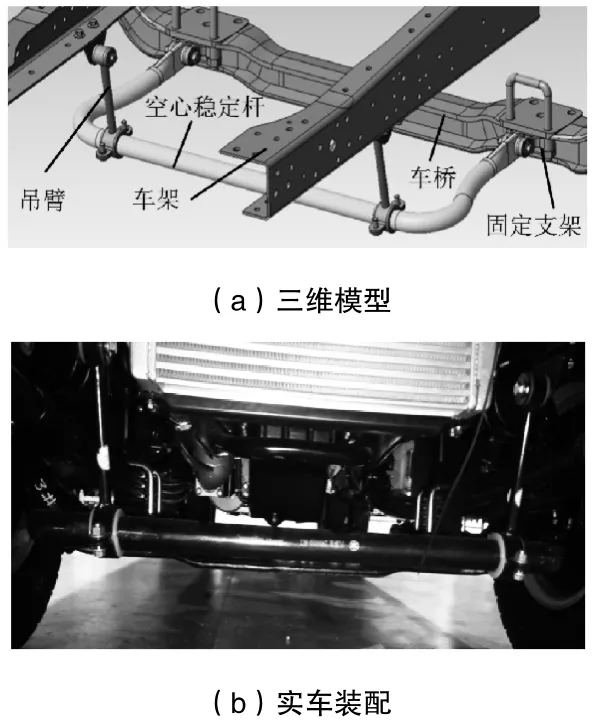
圖1 某輕型商用車前空心穩(wěn)定桿系統(tǒng)

對于輕型商用車來說，車輪側傾角剛度要遠大于彈性元件和穩(wěn)定桿的角剛度，故橋的轉角較小；另一方面，橋中部豎直方向變形很小。由于對稱性，穩(wěn)定桿中部相對于橋中部無變形、無轉角，于是穩(wěn)定桿中部可簡化為固定端。截取空心穩(wěn)定桿一半加以討論，建立其數(shù)學模型如圖2所示（在此未考慮穩(wěn)定桿為避免和其他零件干涉而形成的彎曲部分）。

圖2 空心穩(wěn)定桿數(shù)學模型

在圖2中，A為端點，在該點通過穩(wěn)定桿吊臂與車身相連，AB段為直線段，BC段為圓弧，D點為穩(wěn)定桿與吊臂的連接點，中點E為固定端。d、l1、l2、l3、l4、R為穩(wěn)定桿設計參數(shù)，其中l(wèi)3為穩(wěn)定桿的安裝參數(shù)，其他為穩(wěn)定桿結構參數(shù)。

圖中部分參數(shù)可表示為：l5= l1-l2,

1.1 空心穩(wěn)定桿側傾角剛度

AB 段：PAB(x)=P，MAB(x)=P·x，MxAB(x)=0，（0≦x≦l0）；

BC 段：PBC(θ)=P，（0﹤θ≦β）有

CD段：PCD(x)=P，MCD(x)=Px，MxCD(x)=Pl4

DE 段：PDE(x)=P- Pd，當MDE(x)=P(l1- l3)+ (P-Pd)x，MxDE(x)=Pl4；

上式中，PAB、PBC、PCD、PDE依次為各段的剪力；MAB、MBC、MCD、MDE依次為各段的彎矩，MxAB、MxBC、MxCD、MxDE依次為各段的扭矩，根據(jù)克拉貝依隆原理[2-3]，有：

取P=1時，對上式整理得：

式中，f為穩(wěn)定桿端點A處在單位載荷P作用下的垂直位移；E為抗彎剛度；I為截面慣性矩；μ為泊松比。

由公式（1）可得到穩(wěn)定桿的線剛度為 1/f，則穩(wěn)定桿的側傾角剛度可以表示為：

1.2 空心穩(wěn)定桿應力及危險截面位置

按照圖2所示的受力情況，對穩(wěn)定桿進行應力分析，其各截面所受的最大應力可以表示為：

式中，M、Mx、P分別為各截面的彎矩、扭矩和剪力，W、WP、A分別為各截面處的抗彎截面系數(shù)、抗扭截面系數(shù)及面積，σ、τ1、τ2為各截面M、Mx、P所產生的最大應力。通過式（3）可以計算出穩(wěn)定桿各段各截面所受的最大正、切應力。

穩(wěn)定桿工作時的危險截面有可能在BC段或者D點，對于危險截面有，故可以忽略τ2的影響。下面按照第三強度理論（最大切應力理論）求解穩(wěn)定桿危險截面位置：

BC段任意點的相當應力為：

由式（4）和式（6）可以確定得到穩(wěn)定桿危險點位置及其最大相當應力為：

穩(wěn)定桿的強度條件可以表示為：

式中，σs為材料的屈服極限，ns為許用安全系數(shù)。

空心穩(wěn)定桿質量是穩(wěn)定桿重要的經濟性指標，在此給出穩(wěn)定桿的質量計算公式為：

式中，d1為空心穩(wěn)定桿內徑，ρ為密度。

通過上述計算分析，完成了空心穩(wěn)定桿側傾角剛度、任意截面最大應力的計算，同時按照第三強度理論給出了空心穩(wěn)定桿的危險截面位置。

1 設計參數(shù)對側傾角剛度、最大相當應力和質量的影響

已知某一空心穩(wěn)定桿設計尺寸為：d=36mm，d1=20mm，l1=l2=435mm，l3=340mm，l4=220mm，R=40mm，車身轉角φr=5°。依次將d、l1、l2、l3、l4、R作為變量，求解出各變量對側傾角剛度、最大相當應力和質量的百分比靈敏度為：

圖3 各設計參數(shù)對穩(wěn)定桿側傾角剛度的影響

式中，xi0(i=1,2…,6)為各參數(shù)的初始值，△xi為各參數(shù)的變化值；ki0、σi0、mi0分別為各參數(shù)初始值對應的角剛度、最大相當應力及質量；△xi0、△σi0、△mi0分別為各參數(shù)對應的角剛度、最大相當應力和質量的變化值。以各靈敏度的分母、分子分別作為橫、縱坐標，繪制圖形，結果如圖3、圖4和圖5所示。

圖4 各設計參數(shù)對穩(wěn)定桿最大相當應力的影響

圖5 各設計參數(shù)對穩(wěn)定桿質量的影響

從圖3可以看出，各設計參數(shù)對側傾角剛度影響從大到小依次為：d、l4、l1、l3、R；從圖4可以看出，各設計參數(shù)對最大相當應力影響從大到小依次為：l4、l1、d、l2、l3、R；從圖5可以看出，l3不影響穩(wěn)定桿質量，R對穩(wěn)定桿質量的影響非常小，其余設計參數(shù)對質量影響從大到小依次為：d、l2、l4、l1。綜合分析上述結果，會發(fā)現(xiàn)增大穩(wěn)定桿直徑d可以明顯提高側傾角剛度，但會導致質量增加較多；減小l4也會明顯增加側傾角剛度，也會導致最大相當應力增大明顯；l1的取值大小對側傾角剛度、最大相當應力影響明顯；增加l3會使側傾角剛度增加，最大相當應力減小，同時不會導致質量增加。總之，認知穩(wěn)定桿各設計參數(shù)對其性能的影響，

對合理設計穩(wěn)定桿具有重要的指導意義。

2 優(yōu)化設計

關于空心穩(wěn)定桿的優(yōu)化設計，首先，要保證與操縱穩(wěn)定性直接相關的設計指標，即側傾角剛度；其次，空心穩(wěn)定桿的設計必須滿足強度要求；第三，應盡量減輕空心穩(wěn)定桿的質量，提高其經濟性[4-5]。為此提出穩(wěn)定桿的優(yōu)化設計目標：在滿足布置空間要求、強度條件、側傾角剛度期望值的前提下，設計出質量最小的空心穩(wěn)定桿。

定義空心穩(wěn)定桿優(yōu)化設計變量為：

式中，d、l1、l2、l3、l4、R與圖2中的穩(wěn)定桿設計參數(shù)相一致。

定義優(yōu)化設計的目標函數(shù)為：

優(yōu)化設計的約束條件要充分考慮到空心穩(wěn)定桿的布置空間、剛度、強度、制造工藝及相關零件強度等方面的要求，因此建立下列約束方程為：

（a）為避免空心穩(wěn)定桿下支架內襯套與穩(wěn)定桿圓角部分發(fā)生干涉，有約束方程：

式中，C0為穩(wěn)定桿下支架孔內襯套長度。

（b）穩(wěn)定桿端部與吊臂相連，吊臂上端與上支架相連，為了減小上支架所受的彎曲應力，同時避免吊臂與彈性元件干涉，當穩(wěn)定桿端部在車架外側時要求穩(wěn)定桿端部距車架外側面不能大于C1，有約束方程：

式中，C2為車架外寬，C1為支架懸臂長度，C1越大，則支架應設計得越龐大。

（c）穩(wěn)定桿支架位于車架內側時，穩(wěn)定桿上支架距車架外側的懸臂不能大于C1′，有約束方程：

式中， C1′為支架在車架內側時支架懸臂長度。

（d）穩(wěn)定桿端部打孔，通過連接件與吊臂相連，所以要求端部部分不能為圓弧，必須為直線。有約束方程：

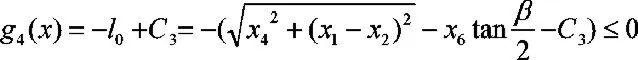
式中，C3為一常數(shù)，要求該常數(shù)能保證裝配時夾具不與穩(wěn)定桿干涉。

（e）穩(wěn)定桿原材料為棒料或者管料，在彎曲成型時圓弧外部受拉，內側受壓，為了避免成型時形成較大的內應力，對半徑與直徑比值提出下限值，有約束方程：

式中，C4為半徑與直徑之比，一般要求大于1.5。

（f）對于穩(wěn)定桿側傾角剛度期望值K及其允許誤差Ke，有約束方程：

（g）按照穩(wěn)定桿的強度要求，最大第三相當應力應小于材料的許用應力，有強度約束方程：

（h）要求圖2中襯套安裝位置D點受力不能太大，否則會削弱襯套的使用壽命，有約束方程：

式中， C5為襯套受力限值。

（i）要求所有設計參數(shù)都大于0，有：

由以上分析可以看出，空心穩(wěn)定桿優(yōu)化設計可以看成是一個6維，9個不等式約束，以質量最小為目標函數(shù)的單目標非線性規(guī)劃問題。

2 利用MATLAB進行優(yōu)化計算

利用MATLAB軟件優(yōu)化工具箱的fmincon()函數(shù)，對優(yōu)化設計模型進行求解。一共建立3個M文件，分別為目標函數(shù)文件、約束函數(shù)文件和原本文件。

為了驗證算法的可行性，以某商用車前懸架為例，對其空心穩(wěn)定桿進行優(yōu)化設計，并與原設計結果進行對比，輸入的原始數(shù)據(jù)如表1所列。

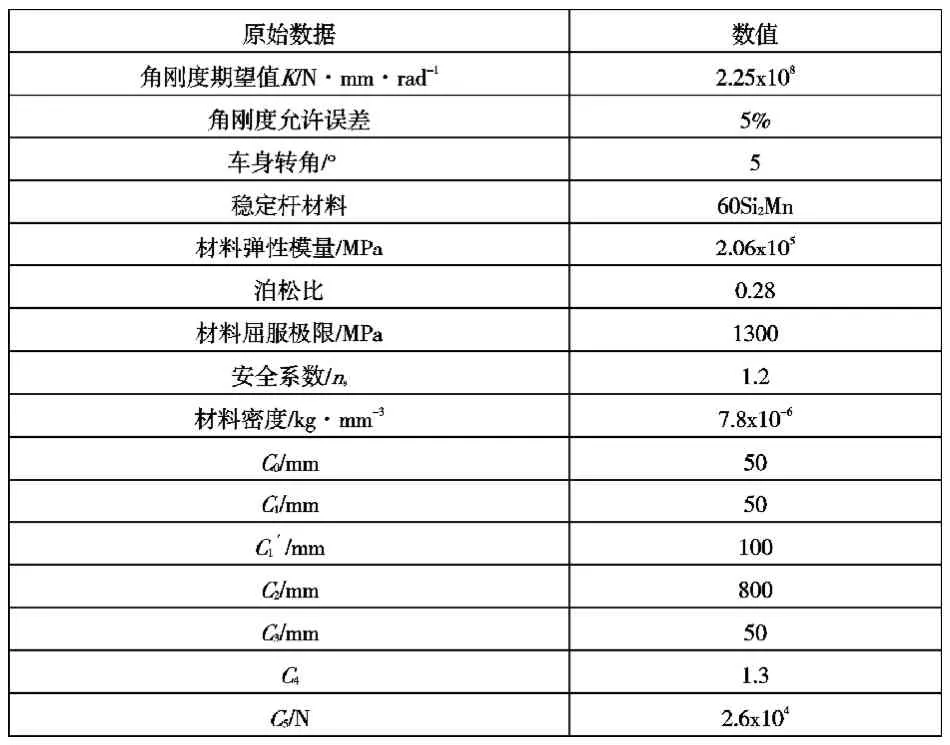
表1 原始數(shù)據(jù)

將表1中的原始數(shù)據(jù)輸入到由MATLAB軟件編寫的優(yōu)化設計程序當中，通過計算分析得出了穩(wěn)定桿優(yōu)化結果，原方案與優(yōu)化結果對比如表2所列。

表2 原方案與優(yōu)化方案結果對比

對比計算結果發(fā)現(xiàn)，在最大相當應力和側傾角剛度相等時，優(yōu)化后的方案質量為原方案的84%，穩(wěn)定桿支撐點D處的受力為原方案的85%，圓角處的曲率半徑與直徑比由原來的 1.1增大為 2.0。另外，從優(yōu)化設計結果對應的約束方程g(x)=[-5 0 -150 -28 -23 0 0 -4401]可以看出，約束條件1、2、6、7同時限制了空心穩(wěn)定桿的質量，為了減輕空心穩(wěn)定桿質量，還可以考慮：

（a）減小襯套軸向尺寸 C0，但這會增大襯套應力，降低其壽命；

（b）增加穩(wěn)定桿上支架的懸臂長度 C1，但這會導致穩(wěn)定桿上支架彎曲應力增大；

（c）減小穩(wěn)定桿剛度期望值，或者增加剛度允許誤差；

（d）增加穩(wěn)定桿許用應力，比如采用屈服極限更高的材料，或者降低許用安全系數(shù)，但前者會增加材料成本，后者會降低穩(wěn)定桿疲勞壽命。

根據(jù)以往的試驗經驗，除合理的選材和合理的設計空心穩(wěn)定桿結構以外，其金相組織和表面質量對壽命的影響非常大，因此必須嚴格控制熱處理工藝和表面質量。關于穩(wěn)定桿重量，采用管材制作的中空穩(wěn)定桿，較實心來說，在保證性能一致的同時能大幅度降重。

3 結束語

（a）空心穩(wěn)定桿與整車平順性和操縱穩(wěn)定性密切相關，空心穩(wěn)定桿必須起到合理協(xié)調整車垂直剛度和側傾角剛度的目的。利用能量法實現(xiàn)了對空心穩(wěn)定桿側傾角剛度、各截面應力的計算和最大相當應力處危險橫截面位置的確定。

（b）利用百分比靈敏度分析了空心穩(wěn)定桿各設計參數(shù)對其側傾角剛度、最大相當應力和質量的影響，得出在設計選取穩(wěn)定桿各參數(shù)時，必須綜合考慮每一個參數(shù)對空心穩(wěn)定桿側傾角剛度、強度、布置空間、重量的影響。

（c）在滿足布置空間、側傾角剛度期望值、強度、制造工藝等眾多條件下，以質量最小為目標，建立了空心穩(wěn)定桿優(yōu)化設計模型，用 MATLAB工具箱便捷地完成了空心穩(wěn)定桿的優(yōu)化設計，優(yōu)化后的空心穩(wěn)定桿在保證性能的前提下，經濟性得到提高，加工工藝得到改善，而且有效地提高了穩(wěn)定桿總成其他零件襯套、支架的使用壽命。

[1] 顧偉清等.空心穩(wěn)定桿設計及實效分析.技術導向,2017.04

[2] 王望予主編.汽車設計.第4版.北京:機械工業(yè)出版社,2004.8.

[3] 聶玉琴,孟廣偉主編.材料力學.北京:機械工業(yè)出版社,2004.2.

[4] 陳家瑞.汽車構造.第三版.北京:機械工業(yè)出版社,2009.2.

[5] 丁能根,張宏兵等.橫向穩(wěn)定桿性能計算及其影響因素分析.汽車技術,2006(1):23～26.