基于多項式迭代的等效旋轉矢量微分方程精確數值算法

嚴恭敏，李思錦，秦永元

（西北工業大學 自動化學院，西安 710072）

在捷聯慣導算法中，目前主流的姿態更新求解方法是先使用陀螺角增量（或角速率）的多子樣采樣計算等效旋轉矢量，補償轉動不可交換誤差，再使用等效旋轉矢量計算姿態更新四元數[1-6]。但是傳統多子樣算法都是在等效旋轉矢量微分方程（Bortz方程）二階近似的基礎上進行推導的，從源頭上看不可避免地存在原理性誤差，使得在大機動環境下選用子樣數越多，精度往往越差[7]。

最近，數位研究者注意到了傳統多子樣算法存在的缺陷，提出了一些改進的新算法。文獻[8-9]考慮了Bortz方程中三階甚至四階項的影響，提出一種改善算法精度的方法，增加了角增量的三階和四階叉乘項進行不可交換誤差補償，但是該方法的推導過程比較繁瑣，難以擴展到五階及以上叉乘運算，原理上精度受限。文獻[10]提出基于四元數微分方程迭代的姿態更新算法，文獻[11]提出基于羅德里格參數微分方程迭代的姿態更新算法，兩者除了使用的數學描述工具不同外，其總體設計思路基本一致，都是在假設角速度為多項式的條件下，通過迭代計算能夠精確給出姿態更新的數值解。相比而言，前者在表示形式上更為簡潔且計算量稍少一些。類似于上述兩種迭代算法，本文將利用Bortz微分方程給出基于多項式迭代的等效旋轉矢量精確數值算法，有效避免了原理性近似誤差。同時，本文對算法的精度和和收斂速度進行了分析。研究結果表明，與四元數迭代方法相比，新算法具有同樣的數值計算精度，且計算量相當，具有較好的應用價值。

1 算法理論分析

1.1 迭代算法推導

等效旋轉矢量微分方程（Bortz方程）為[1]

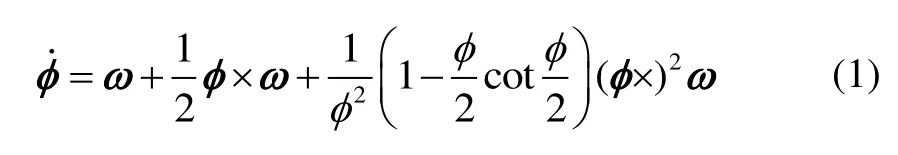
其中，ω為動坐標系相對于參考坐標系的轉動角速度矢量，φ=φ為等效旋轉矢量φ的模值。將式(1)中的余切函數作泰勒級數展開，經整理后可得：

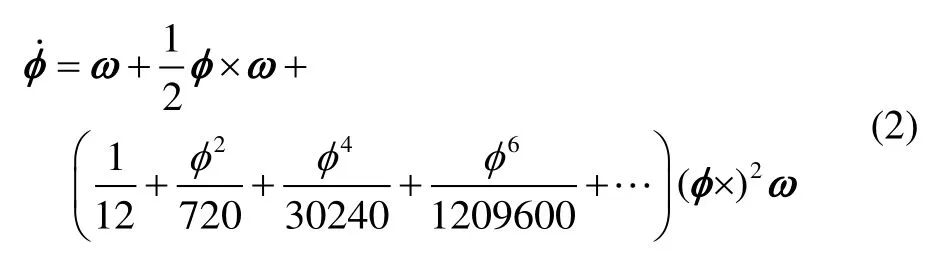
式(2)兩邊同時在時間區間[0,t]上積分，得：

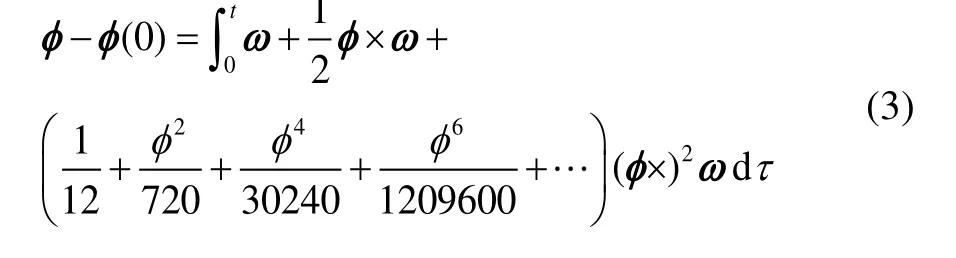
將式(3)左邊φ(0)移到右邊，并改寫成迭代的形式，有：

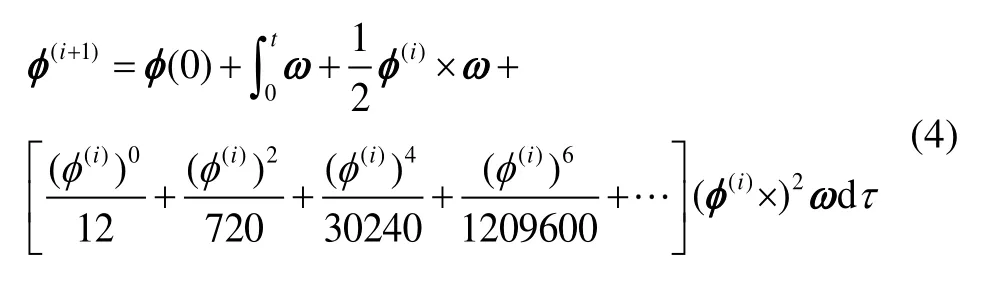
其中，φ(i)(i=0,1,2,…)表示第i次迭代的等效旋轉矢量，且有迭代初值φ(0)=0。不失一般性，可令初值φ(0)=0。

假設角速度ω為時間t的有限次（N-1次）多項式：

如果實際陀螺采集的為N子樣的角增量數據，則可先按文獻[10]的方法變換為上述角速度多項式，再使用本文方法。

再假設經過第i次迭代后的等效旋轉矢量φ(i)多項式為

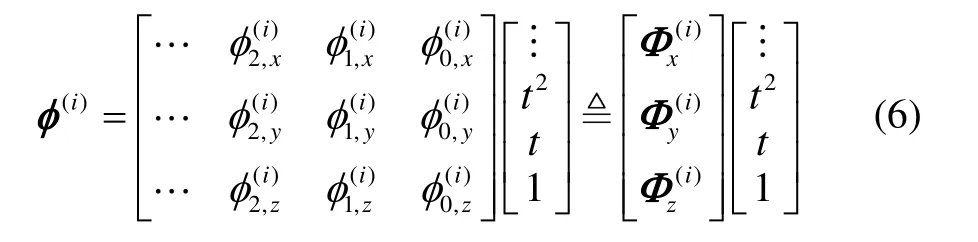
注意到式(4)中φ(i+1)為多項式的積分，因而φ(i+1)（或φ(i)）的多項式零次項系數必為 0，即有

將式(5)和式(6)代入式(4)右端的被積函數各項中作進一步計算，有：

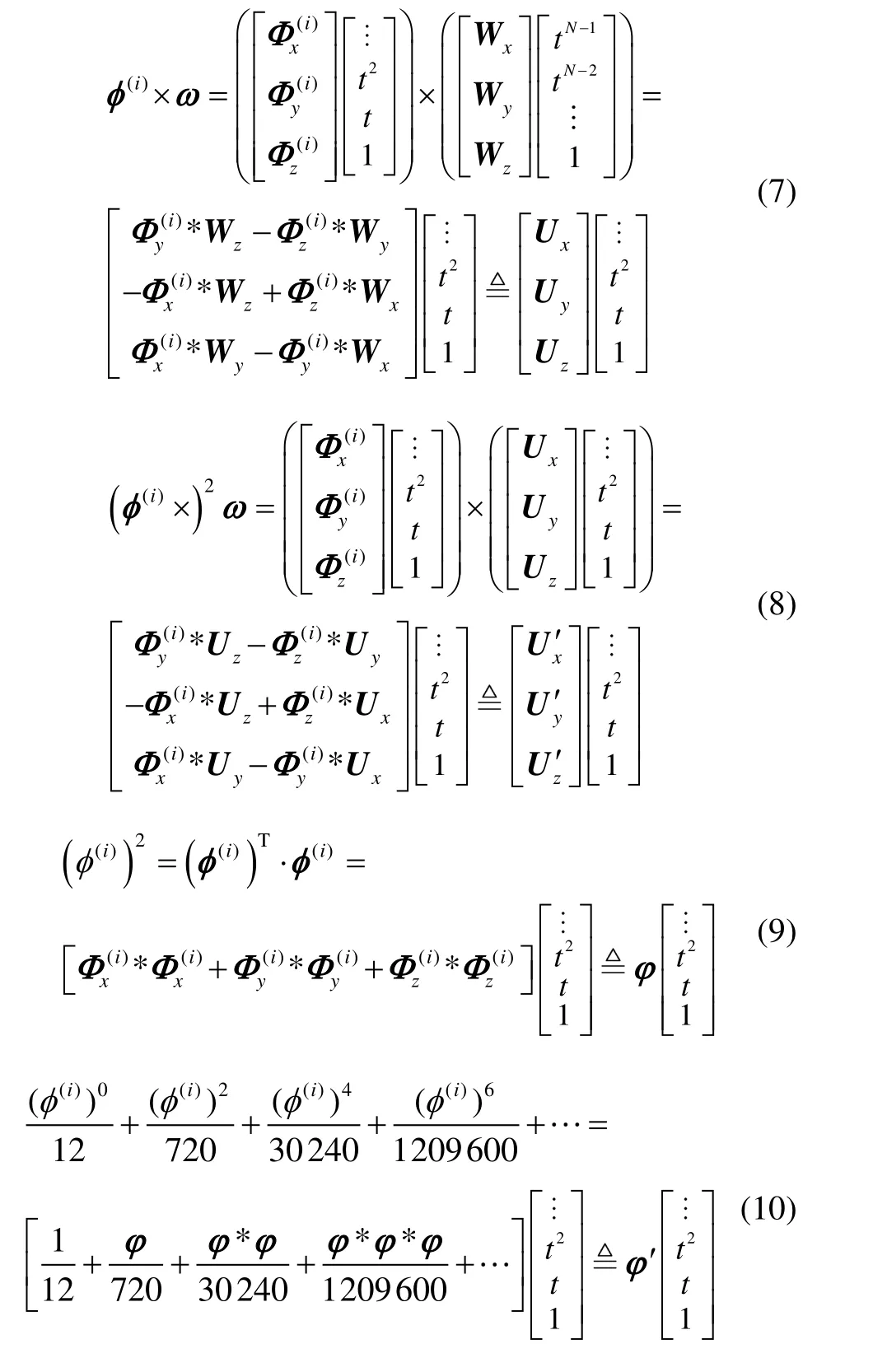
其中，運算符“*”表示兩個多項式系數向量之間的卷積運算。

再將式(5)(7)(8)(10)代入式(4)，可得：

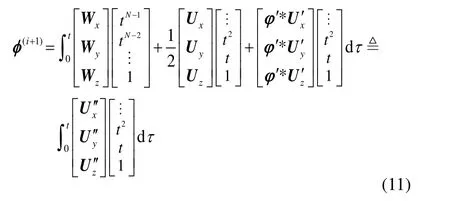
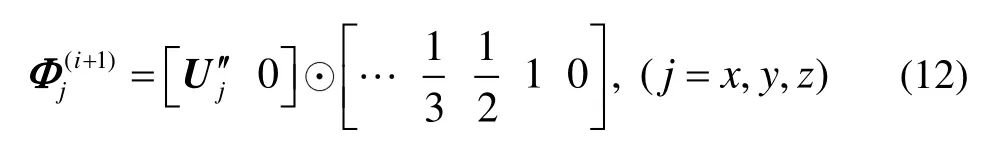
1.2 精度分析

在實際利用計算機進行求解時，需對式(4)中的余切函數展開取有限階次。一般角速度的零次項多項式系數不為0，則當迭代次數時，多項式的不為 0的最低冪次為 1。如果存在不可交換誤差，的多項式表示系數中不為 0的最低冪次一般為2不為0的最低冪次為3不為0的最低冪次為()。因此，若忽略了式(4)右端被積函數中與模值有關的不小于的所有項，則將可能影響被積函數次冪的計算準確性，再經過積分之后等效旋轉矢量多項式的階精度會受到影響。換句話說，若忽略及其以上項后，等效旋轉矢量的多項式解在理論上只具有階精度。

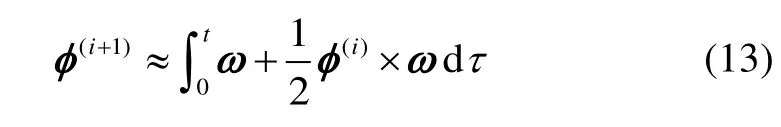
作為對比，傳統的基于等效旋轉矢量泰勒級數展開法的多子樣算法是在如下近似公式(14)的基礎上作進一步推導的。

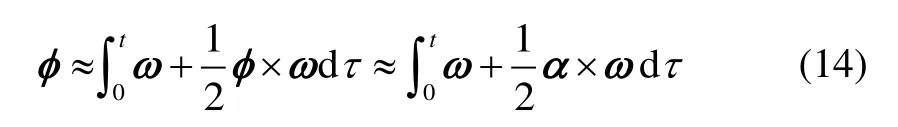
在保留余切函數展開無窮冪次的情況下，式(4)理論上是嚴格成立的，即對于均成立。但如果僅保留有限冪次，為了保證等式近似程度足夠高，必須使余切函數展開的高冪次項迅速衰減，以至于在數值計算上誤差可以忽略不計。

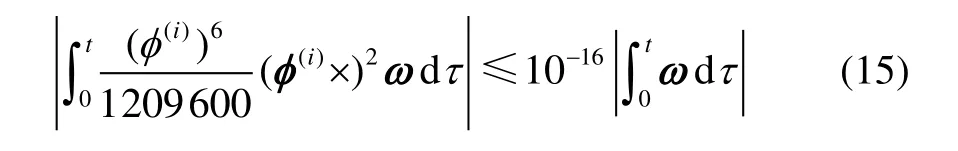
式(15)可近似為（實際上是條件變嚴格了）：

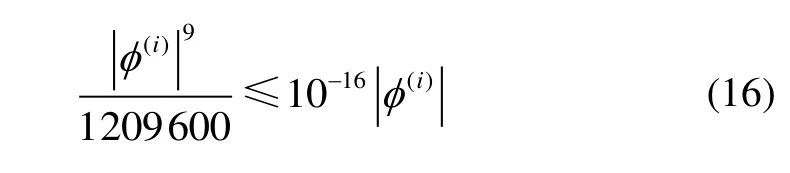
由式(16)求解得：

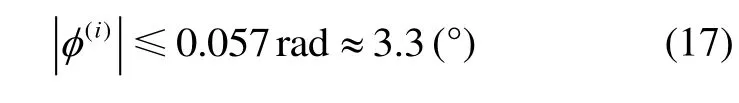
這意味著，在更新周期[0,t]內，如果等效旋轉矢量模值（可近似為角增量模值變化）小于 3.3°，則在計算時可忽略及更高冪次項的影響。

1.3 計算量分析

傳統機械設計作業中主要存在的問題之一即為：設計成本較高。具體分析設計成本高主要體現為：設計產品通過生產線進行生產制造，并基于實際生產的機械設備進行性能，質量等基礎參數的測試。實際測試中如出現問題則需重新生產制造，從而造成了設計成本高的現象。分析自動化技術在應用中通過在線模擬測試的方式，有效的對機械裝置的力學性能，結構安全性，進行了完善的測試和評估。后期結合3D打印技術進行相關設計成果的制造，有效的降低了生產線生產產生的高設計成本現象。

2 仿真驗證

2.1 圓錐運動誤差仿真

圓錐運動和多項式角運動常常用來評價姿態更新算法的精度優劣，下面也采用圓錐運動環境來對比本文算法與傳統優化圓錐算法的姿態解算精度。

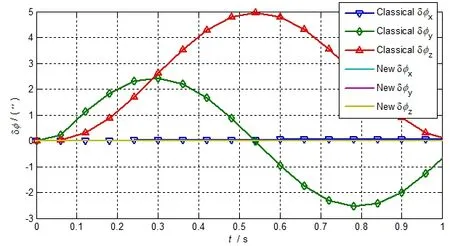
圖1 圓錐運動算法誤差對比Fig.1 Comparison on algorithm errors of coning motion

從圖1中可以看出，傳統算法在錐軸上的漂移誤差逐漸變大，在1 s時為0.1″，在非錐軸上的誤差呈周期性變化，最大達到了5″；而新算法的三軸誤差始終都很小，經放大觀察僅為10-7″量級。這說明，如果出現不規則非整周期的圓錐運動，傳統算法可能會引起較大的姿態解算誤差，而新算法能近乎完美的解算復現真實的姿態運動，新算法對于復雜的角運動具有非常高的求解精度。

進一步仿真表明，本文算法與文獻[10]所提的四元數迭代算法具有同等數值精度，更多的仿真情況可參考文獻[10]，這里不再贅述。

2.2 迭代收斂性仿真

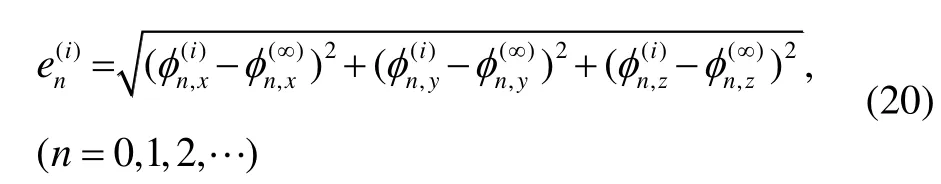
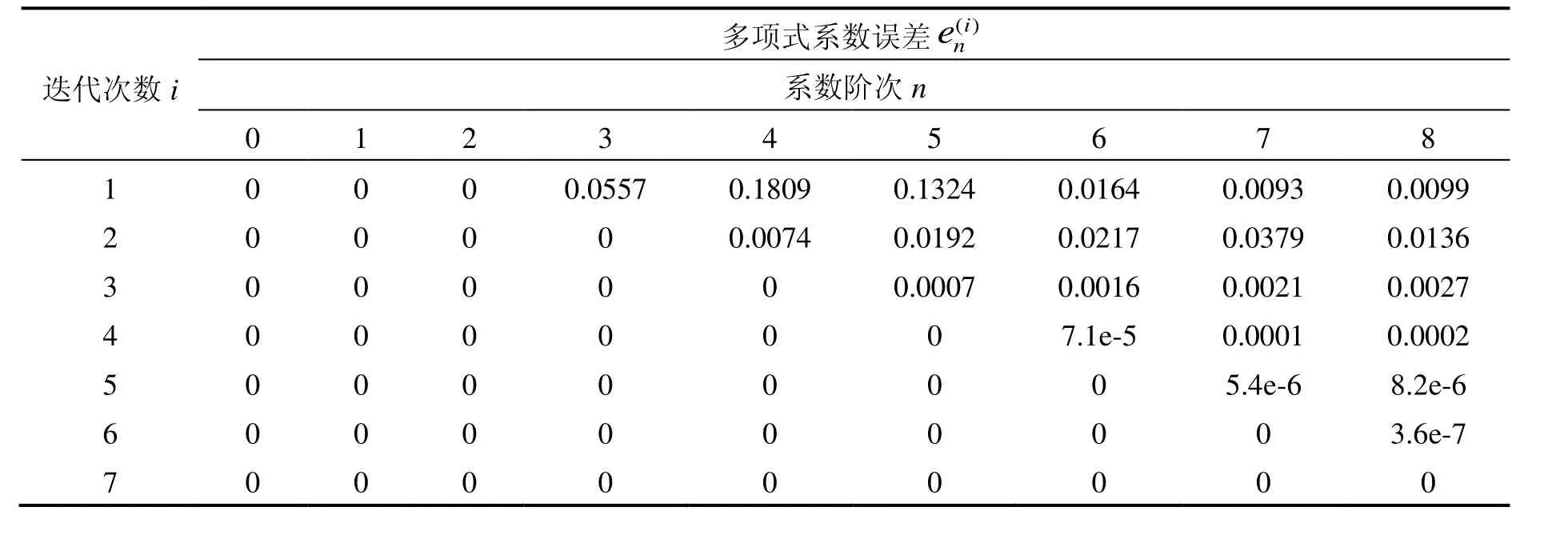
表1 各階多項式系數誤差收斂特性Tab.1 Convergence of polynomial coefficient errors

由表1可見：第1次迭代后，2階項系數誤差為0（收斂）；之后每增加1次迭代，收斂階數加1；經過6次迭代后，7階項系數完全收斂。這表明，等效旋轉矢量迭代收斂的速度是很快的，從而決定了算法的計算量不是太大。

3 與羅德里格參數迭代法的對比討論

同Bortz方程(1)的結構相似，羅德里格參數微分方程為[11]

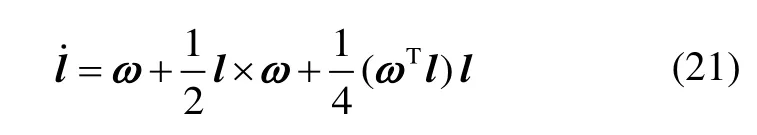
前文1.1節分析的迭代方法也可應用于式(21)，迭代公式為

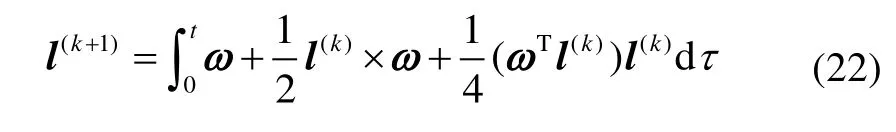
采用式(22)迭代的優點是不含三角函數運算，計算量會比式(4)更少（約減少三分之一）。此外，在實際計算時式(4)需截取余切函數的有限項，使得存在如式(17)所示的角速度范圍限制，而式(22)在理論上對任意角速度都是迭代收斂的。

仿真還表明，迭代式(22)也具有如表1所列的收斂特性。當然，與羅德里格參數表示相比，采用等效旋轉矢量的優點是物理意義更直觀，方程(21)右端的第三項意義不夠直觀，而方程(1)右端的第二、三項均表示不可交換誤差，所以本文關于等效旋轉矢量迭代的研究結果容易直接與很多已有的傳統多子樣算法成果進行對比。

4 結 論

傳統圓錐誤差補償算法在純圓錐運動環境下且半錐角比較小時是非常有效的，然而對于大錐角情況或者應用于大角度機動環境，都會產生較大的姿態漂移誤差。

為了避免這一問題，本文根據Bortz方程構造了多項式積分迭代公式，給出了一種新的直接求解等效旋轉矢量的數值算法，在算法推導過程中考慮了不可交換誤差高階項的影響，算法計算精度高，具有與四元數微分方程迭代解相同的數值精度[10]。通過與傳統的基于等效旋轉矢量的多子樣算法對比仿真，驗證了新算法在大幅值圓錐運動條件下具有明顯的精度優勢。新算法的計算量較小，具有較好的應用價值。