矢量頻率跟蹤輔助鎖相環的設計與實現

王 前，金 天，吳雨航，鄧若凡

（1. 西安郵電大學 電子工程學院，西安 710121；2. 北京航空航天大學 電子信息工程學院，北京 100191）

矢量頻率鎖定環路（VFLL）是矢量跟蹤環路的一種，最早由Pany等提出[1]，其設計思想與較早出現的矢量延遲鎖定環路（VDLL）類似，都是采用多通道聯合處理的方式進行載波頻率或碼相位的跟蹤[2]。然而傳統 VFLL環路無法準確跟蹤載波相位，不能利用載波相位平滑偽距，導致定位精度和測速精度不夠高。

針對上述問題，研究人員開始將VFLL與鎖相環（PLL）結果相結合。由于VFLL環路相比于傳統頻率跟蹤環路（FLL）具有更高的頻率跟蹤精度，因此融合之后的跟蹤環路理論上能夠提高跟蹤環路的性能。前期研究人員的融合方法種類較多。Stefan等人的仿真結果[3]表明，可以將PLL環路的結果與VFLL環路進行融合來提高環路相位跟蹤精度。Deambrogio和 Macabiau等人的文章用矢量方法提升了電離層閃爍情況下的載波跟蹤性能[4]。胡輝等人的研究結果指出對于高動態的 GPS載波跟蹤需要多種手段的組合[5]。Jiang等人利用模糊邏輯的方法將FLL與PLL跟蹤進行融合[6]。Zhao等人的研究指出了矢量 PLL電文解調方法，并對此開展了理論性能分析[7]。謝非等人[8]提出了基于快速相關的矢量跟蹤算法，使跟蹤性能得到提升。

本文在上述研究基礎之上，結合二階FLL輔助三階PLL（FAPLL）的結構，設計了一種將VFLL頻率鑒別結果和PLL相位鑒別結果進行融合的方案，再通過載波相位平滑碼偽距提高接收機偽距測量精度，給出了其理論性能分析，并通過軟件接收機和模擬仿真數據進行了測試，驗證了上述方法的性能提升。

1 設計思路

在傳統接收機中，頻率跟蹤環路（FLL）只能夠實現對頻率的跟蹤，無法獲得載波相位信息。為精確獲得載波相位信息，Ward等人提出了FLL輔助PLL算法（FAPLL）[9]。該算法將FLL和PLL計算得到的頻率和相位鑒別結果進行了融合，通過FLL輔助PLL的方式獲得較為精確的相位估計值。

隨著矢量跟蹤技術的發展，VFAPLL環路設計逐漸得到了重視。與傳統FLL環路獨立處理各通道不同，在VFLL環路中所有通道的載波跟蹤結果被同時處理，充分利用了對于同一用戶不同衛星運動狀態之間的相關性，提升了載波頻率的跟蹤精度。

為了進一步提升跟蹤性能，本文將VFLL代替傳統的FLL來實現對PLL環路的輔助（VFAPLL）。圖1所示為VFAPLL實現結構圖。VFLL各個通道首先通過鑒頻器得到各個通道頻率測量值和頻率測量誤差，由卡爾曼濾波器融合全部通道的信息，最終給出載體速度估計值與接收機鐘漂。

圖1 VFAPLL實現結構Fig.1 Implementation structure of VFAPLL

上述結果經過映射函數利用各通道的衛星相對位置得到各個通道的頻率估計值，與PLL計算得到的相位估計值同時進入環路濾波器進行融合，濾波得到的最終結果反饋給NCO。

在上述過程中，從接收機速度、鐘差估計值到各通道頻率估計值的映射過程是借助于VFLL算法中接收機和各衛星之間的投影關系完成的，而在傳統FLL輔助PLL算法中并不涉及這一投影關系。

在圖1中，載波頻率的測量一般可采用四象限頻率鑒別器計算，即：

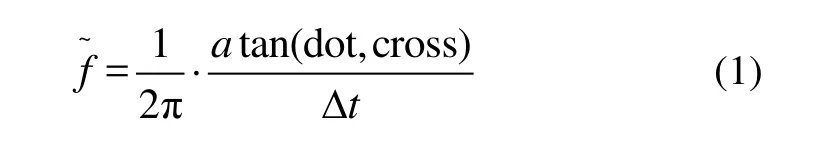
在VFLL環路中，對某顆衛星而言用戶接收到的信號實際頻率與載波頻率、衛星和載體之間的相對速度和接收機鐘漂有關，即：

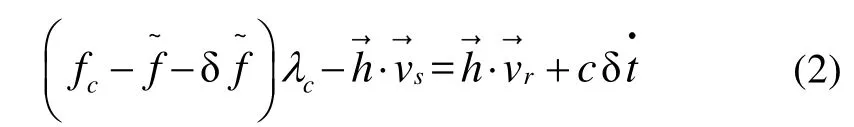
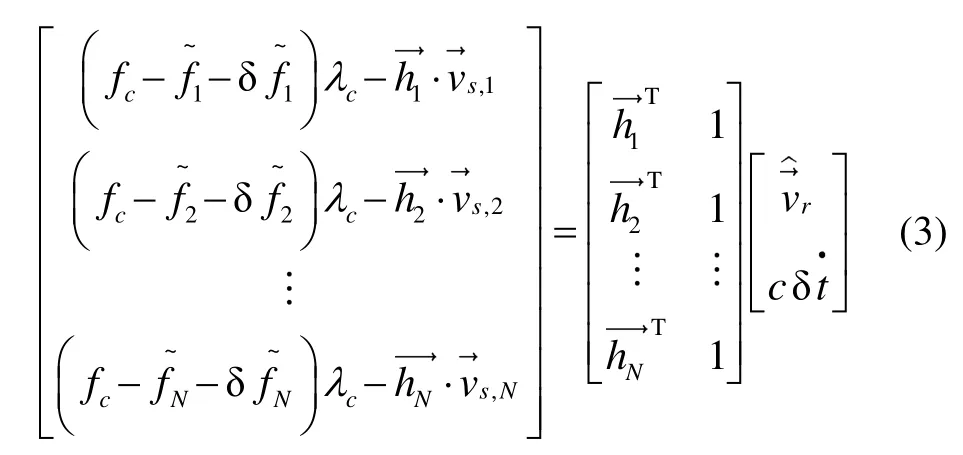
由載體速度估計值和接收機鐘漂得到各通道載波頻率估計值的映射函數可以寫為：

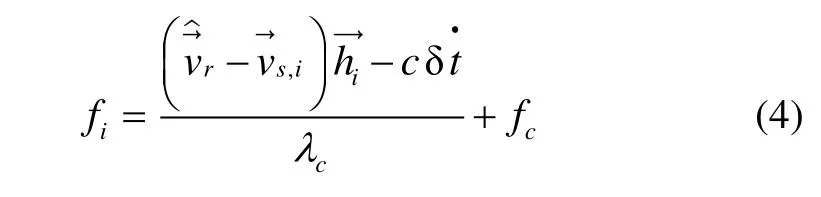
根據文獻[3]和[9]，由于VFLL在頻率測量精度方面優于 FLL，采用VFLL頻率測量結果代替 FLL對PLL進行輔助可以使接收機載波相位觀測精度得到提高。為了更精確地評價上述指標，本文對具體環路參數的設置和融合方法進行了詳細分析。

2 融合方法

2.1 載波頻率與相位信息融合方法

根據現代控制理論，當鎖相環環路階數不低于三階時可以對斜升激勵實現穩定跟蹤。考慮到現實中衛星導航信號經常存在加速場景，常采用二階FLL輔助三階PLL。因此，VFAPLL環路可以采用采用同樣的方法進行頻差和相差的融合，即利用同等維數的VFLL跟蹤環路代替FLL跟蹤環路，通過提高頻率部分的跟蹤性能來達到提高整體環路性能。

圖2所示為VFAPLL環路融合算法信號流程圖，其中，f為各通道頻率估計值，為各通道相位估計值，為融合后的載波相位估計值，T為環路更新時間，、分別為FLL和PLL特征頻率。VFLL、PLL分別采用二階和三階濾波器，圖2中環路濾波參數滿足：

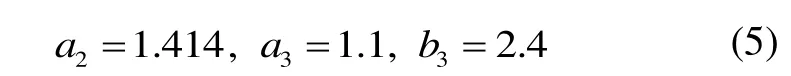
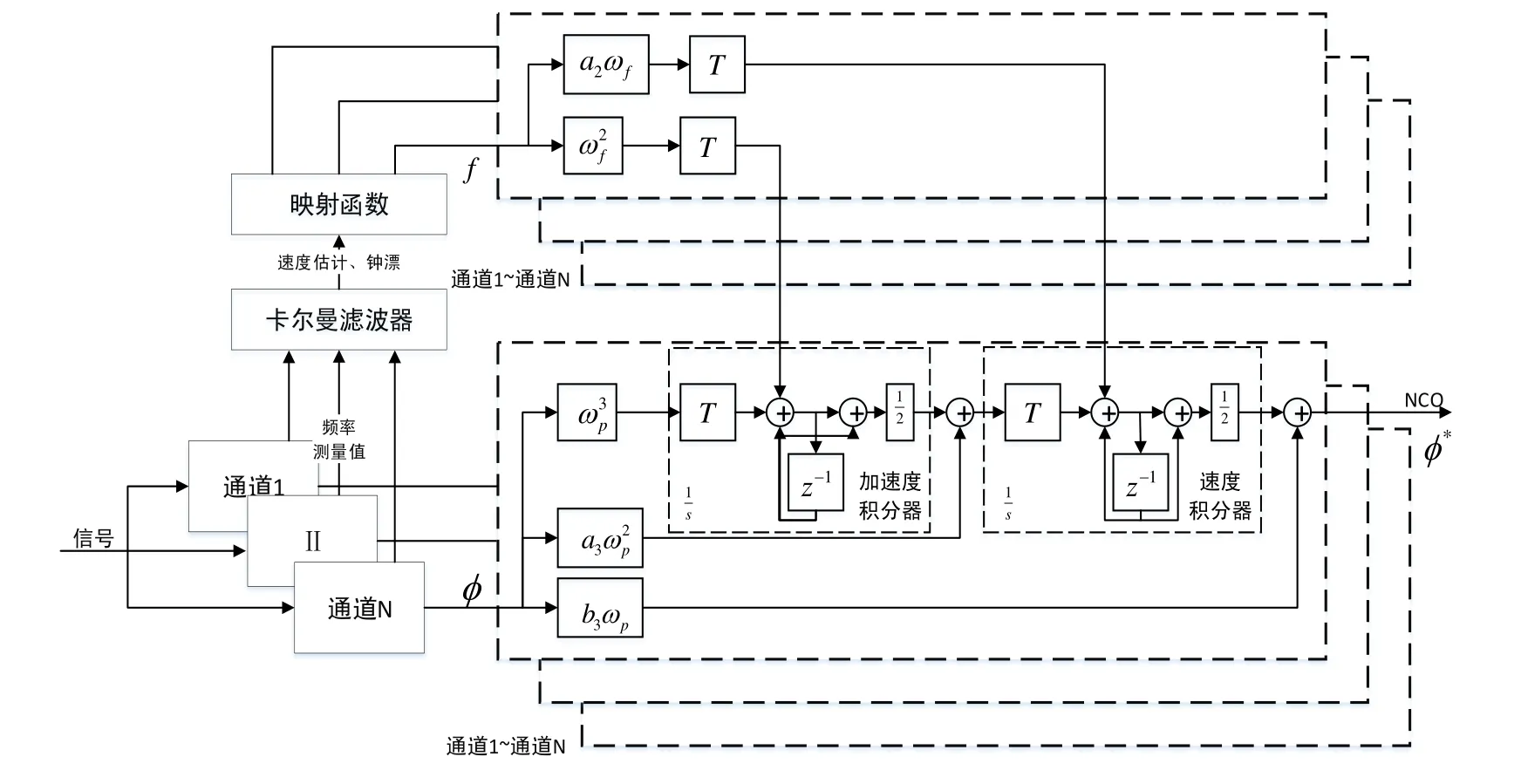
圖2 VFAPLL融合算法信號流程圖Fig.2 Flow chart of VFAPLL fusion algorithm’s signals

在上述結構中，VFLL計算得到各通道頻率估計值經過積分后與PLL融合，整個融合函數為一個雙輸入單輸出系統其輸出為：

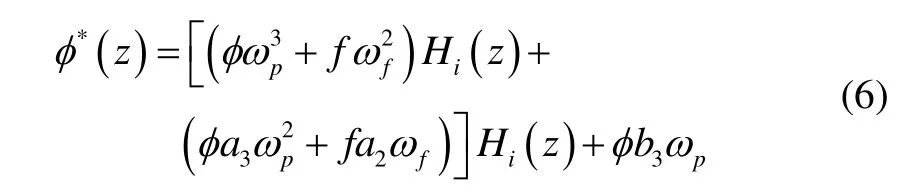
式中，ai和bi為不同階數的濾波器參數，與式(5)對應；為離散積分器傳遞函數：

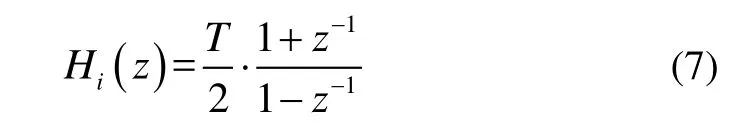
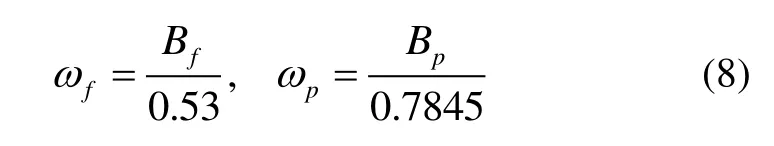
2.2 載波相位平滑碼偽距方法

在實際定位中，直接碼偽距測量結果精度較低但不存在模糊度，接收機常使用精確度較高的載波相位測量值對碼偽距進行一定程度的平滑處理，其中一種常用的整合兩種測量值的方法為：

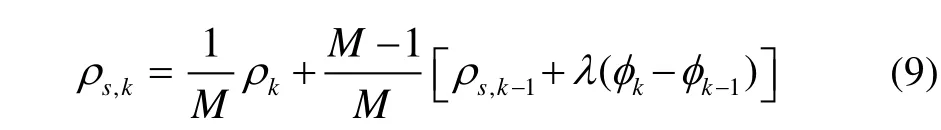
根據文獻[10]，當相關器間距D，前端帶寬和偽碼碼寬滿足時，碼環由熱噪聲導致的碼相位測量誤差可以表示為：

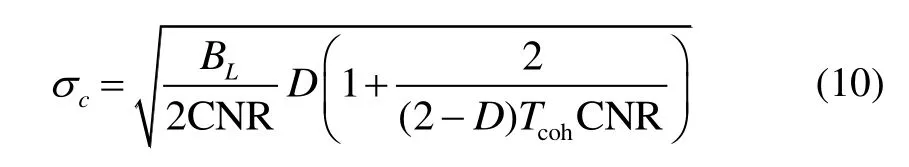
根據式(10)，當信號載噪比為 44 dB?Hz，碼環帶寬 0.2 Hz，相干積分時間 1 ms，前后相關器間距 0.5碼片時，計算得到≈0.42 m(GPS C/A 碼)。

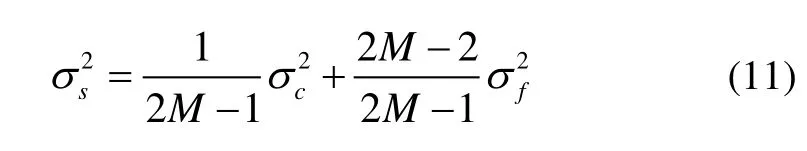
由式(11)，平滑時間常數M越大，碼偽距平滑后測量誤差越接近于載波相位測量誤差。

3 性能測試

由于多通道聯合的 VFLL跟蹤精度要高于 FLL跟蹤精度，因此圖2結構中上方的頻率精度會有所提高，從而提升了融合濾波的精度。

為了有效對比VFLL輔助PLL和FLL輔助PLL這兩種結構在相同條件下的精度性能，這兩種結構中的環路濾波器保持一致，參數、、由式(5)給出，環路濾波器帶寬和分別為25 Hz和20 Hz。

3.1 靜態場景

在靜態場景下，可見衛星數量為 10顆時，使用模擬器提供載噪比約為44 dB?Hz的GPS L1信號，以軟件接收機形式對VFAPLL環路進行性能測試，定位結果更新率為25 Hz。本文對其中的10000個定位結果的測速精度進行了計算，得到的接收機平均測速精度如圖3所示，其中 VFAPLL環路平均測速誤差為0.0453 m/s，FAPLL環路為0.0775 m/s。實驗結果顯示，VFAPLL環路能夠有效提高鎖相環測速精度，相比于FAPLL環路提高約42%。

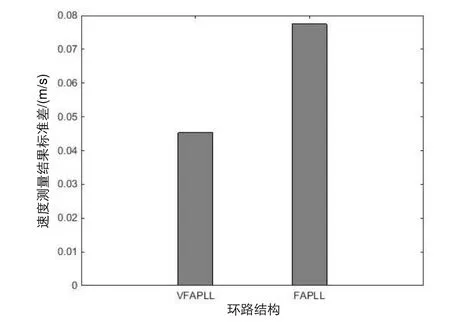
圖3 靜態VFAPLL和FAPLL速度測量柱狀圖Fig.3 Histogram of static VFAPLL and FAPLL velocity measurements

圖4為VFAPLL環路與FAPLL環路載波相位跟蹤精度對比。其中，VFAPLL載波相位測量誤差為0.51 mm，傳統FAPLL載波相位測量誤差為0.61 mm。

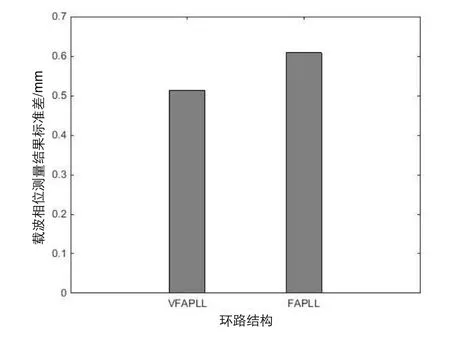
圖4 載波相位跟蹤精度柱狀圖Fig.4 Histogram of carrier phase tracking accuracies

由圖4可知，與FAPLL相比，VFAPLL能夠使環路載波相位測量精度提高約16%。

對于碼相位平滑精度而言，根據式(11)可知，利用VFAPLL載波相位對碼偽距進行平滑，還能夠進一步提高接收機定位精度。

3.2 動態場景

在相同條件下，本文還對具有一定動態的場景進行了仿真，在靜態場景中增加了20 m/s的運動速度。對不同環路測速精度進行了統計比對，如圖5所示。

圖5中VFAPLL環路平均測速誤差為0.0388 m/s，FAPLL環路平均測速誤差為0.0656 m/s，VFAPLL環路測速精度比FAPLL提高了41%。

圖5 低動態VFAPLL和FAPLL速度測量柱狀圖Fig.5 Histogram of low dynamic VFAPLL and FAPLL velocity measurements

3.3 不同場景定位誤差效果圖

圖6～7為靜態和動態場景下，FAPLL和VFAPLL經過載波相位平滑偽距的定位結果。由圖6～7可以明顯看出，在同等PLL和FLL環路濾波器帶寬取值情況下，VFAPLL比FAPLL載波相位輔助碼環路的定位結果更加精確。

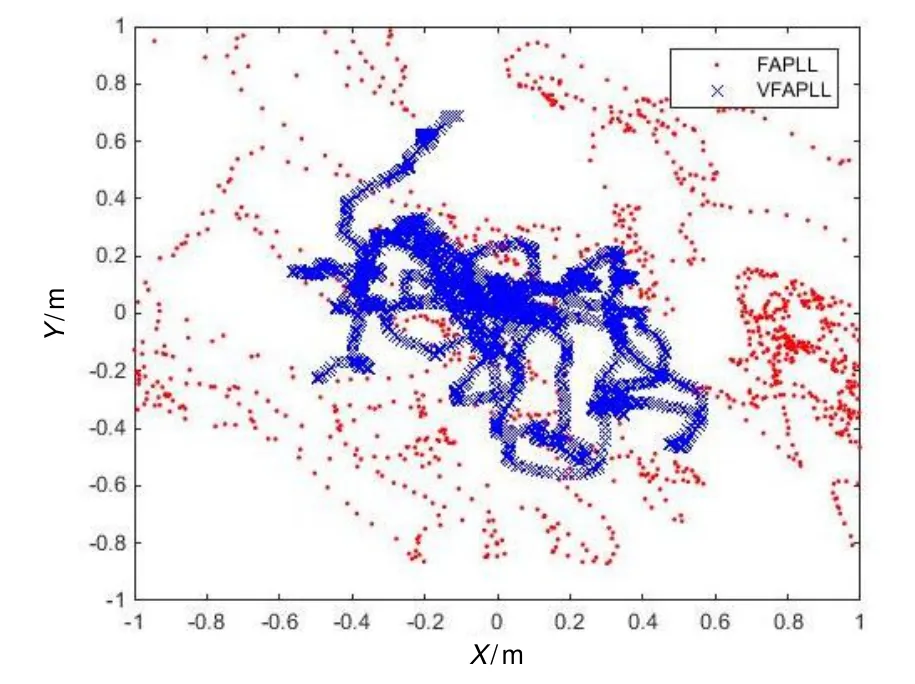
圖6 FAPLL和VFAPLL靜態定位誤差散點圖Fig.6 Scatter diagram of static positioning errors of FAPLL and VFAPLL

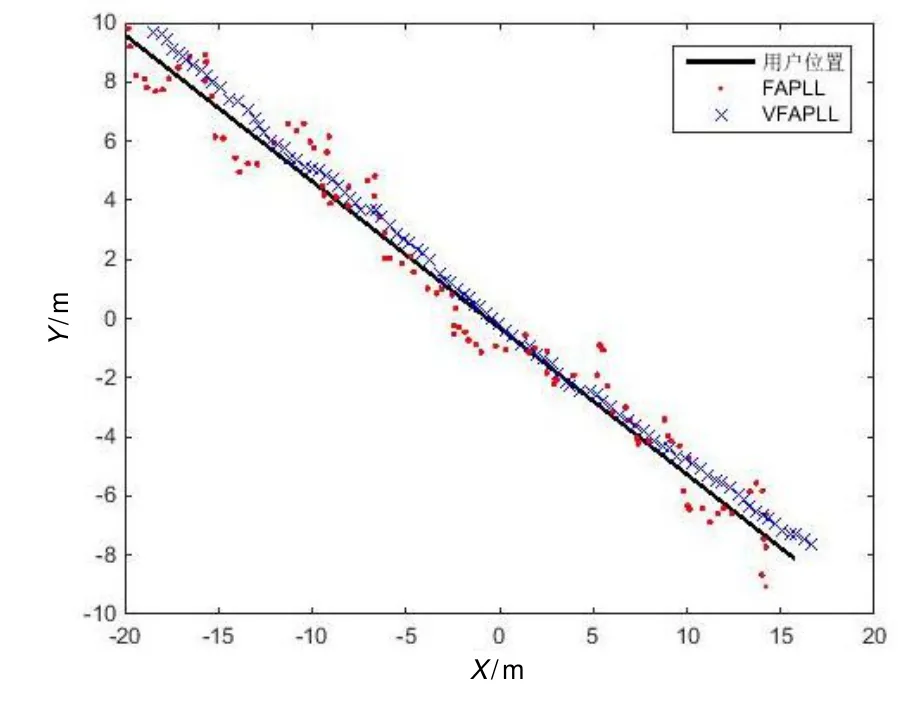
圖7 FAPLL和VFAPLL動態定位誤差散點圖Fig.7 Scatter diagram of dynamic positioning errors of FAPLL and VFAPLL

為了說明接收機性能提升的原因，接收機在傳統環路定位穩定后的第400個定位時刻（第16 s）切換為矢量環路。圖8所示為切換矢量跟蹤前后接收機速度解算結果曲線對比。從圖8中可見，切換矢量跟蹤后接收機速度解算結果波動明顯低于標量環路，從而使得接收機定位解算結果更加精確。

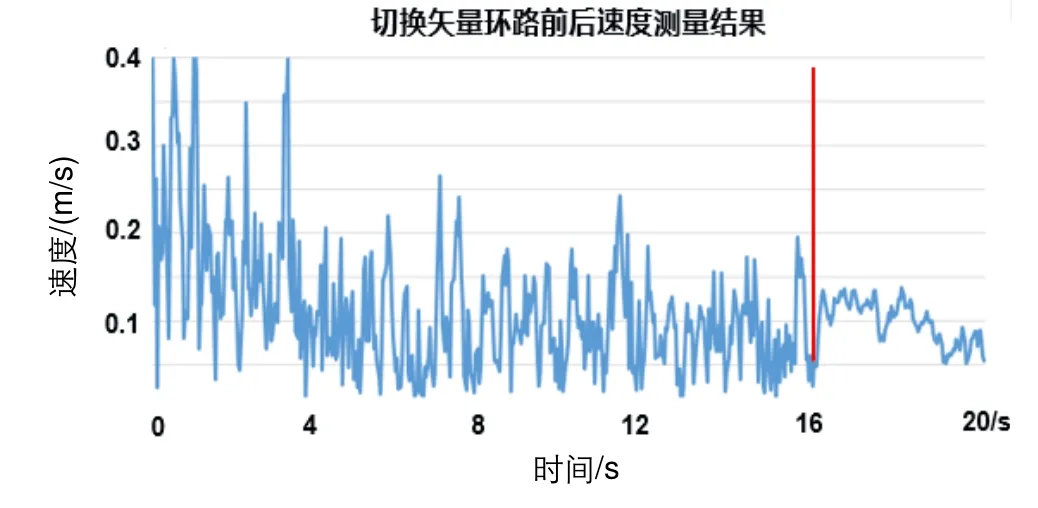
圖8 切換矢量環路前后速度測量結果對比圖Fig.8 Comparison on velocity measurement results before and after switching vector loop

4 結 論

本文研究了矢量頻率環輔助鎖相環的實現結構，給出了頻率估計值和相位估計值的融合方法，并通過軟件接收機對上述結構進行了對比驗證。

實驗結果證明，上述方法在測速精度方面較傳統FAPLL環路提高40%左右，在載波相位精度方面較傳統FAPLL環路提高16%左右。由于VFLL具有較為精確的載波頻率測量精度，使用VFAPLL能夠彌補傳統矢量跟蹤環路在載波相位測量方面的不足，獲得準確的載波相位測量結果。同時，利用VFAPLL測得的載波相位平滑碼偽距后，能夠提高接收機偽距測量精度，獲得比傳統FAPLL更高的定位精度。