舉題說法:“直線、圓”典型問題探究
徐茂炳

【編者的話】親愛的同學們,解析幾何的本質是利用代數方法解決幾何問題,這類問題的突破口往往是圖形,然后把問題“臺階式”分解,達到化大為小的目的.希望今天的探究能幫助大家突破直線和圓方面的難點.
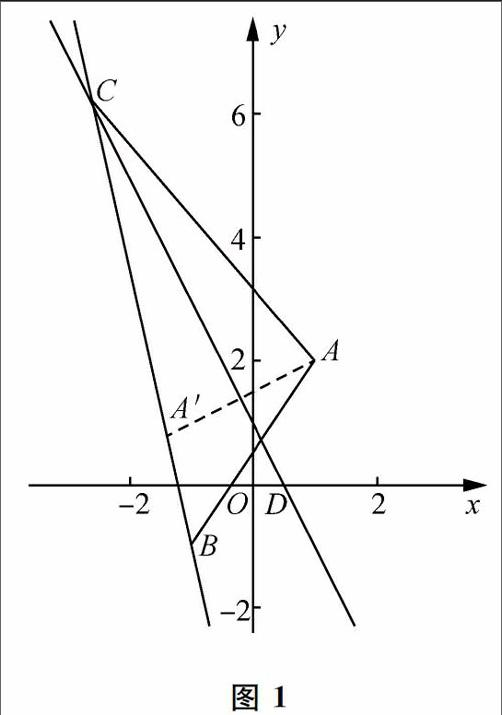
1.已知△ABC的一條內角平分線CD的方程為2x+y-1=0,兩個頂點為A(l,2),B( 1, 1),求頂點C的坐標.
同學們,題目要求我們求出點C的坐標,一般情況我們先設出其坐標,然后如何利用角平分線建立等量關系呢?初中我們知道“角平分線上的點到角的兩條邊距離相等”,從這個結論出發求解的難點是什么?(直線AC,BC方程比較復雜)那么角平分線還有什么性質呢?
請問,“已知三角形兩個頂點A,B和另一頂點C的角平分線,我們如何作出頂點C?”我們可以作A關于直線l的對稱點A',然后直線A'B和l的交點即為點C.
解 設點A關于直線的對稱點A'(m,n),則直線2x+y-1=0是線段AA'的中垂線,所以(n-2)/(m-1)=1/2,2×(m+1)/2+(n+2)/2-1=0,
即m-2n=-3,2m+n=-2
解m=-7/5,n=4/5.所以A'(-7/5,4/5)
(這個方程組怎么來的?中垂線即垂直平分線,垂直利用斜率,平分利用中點)
因為B(-l,-1),所以直線BC的斜率為9/2,所以直線BC的方程為y=-9/2x-11/2.所以聯立方程組y=-9/2x-11/2,2x+y-1=0,解得x=-13/5,y=31/5,所以點C的坐標為(-13/5.31/5)
2.求證:四點A(O,1),B(2,1),C(3,4),D(-1,2)共圓.
同學們,如果給你四個點,你如何判斷四點共圓?
思路1,根據不共線的三點共圓,我們可以求出其中三個點構成的圓的方程,然后用第四個點檢驗;思路2,四邊形對角互補.
那么從計算角度來說,思路1比較好操作.已知三點求圓的方程,我們可以設一般方程,然后解三元一次方程組,也可以聯立垂直平分線的方程組(尺規作圖的過程).
證明 因為A,B,C三點不共線,(為什么交代這個?這三點的選擇有沒有要求呢?)
所以設過A,B,C三點的網的一般方程為x2+y2+Dx+Ey+F=O,
(如果設方程(x-a)2+(y-b)2=r2,r>O,則先求線段AB和線段AC的中垂線,請同學們自己試試看,并比較解法間的難易)所以,代入得1+E+F=0,5+2D+E+F=0,25+3D+4E+F=0
解得D=-2,E=-6,F=5所以網的方程為X2+y2-2X-6Y+5=0.
因為D(-1,2)代入網的方程滿足1+4+2-12+5=0,所以A,B,C,D四點共圓.
3.過點P(3,0)有一條直線Z,它夾在兩條直線l1:2x-y-2=0和l2:x+y+3=0之間的線段恰好被P平分,求直線l的方程.
題目要求我們已知一點P求直線l的方程.一般情況我們設其斜率為k(這時候容易漏掉斜率不存在的情況,這是點斜式的缺陷),然后聯立方程組,由直線l和l1.求點A,直線l和2:求點B,利用AB的中點為P即可解答,
解 設直線l與1,的交點為A,直線l與l2:的交點為B.
當Z的斜率不存在時,A(3,4),B(3,-6)不成立(同學們,防止漏掉斜率不存在的情況);
當l的斜率存在時,設直線Z的方程為y=k(x-3),2x-y-2=0,y=k(x-3),解得x=(3k-2)/(k-2),y=4k/(k-2),所以A((3k-2)/(k-2),y=4k/(k-2))由x+y+3=0,y=k(x-3),解得x=(3k-3)/(k+1),y=6k/(k+1),所以B((3k-3)/(k+1),-6k/(k+1))
(方程組中把k看成常數,解方程組是這道題的難點,消元求解)
因為P為線段AB的中點,所以4k/(k-2)-6k/(k+1)=0.
(這個等式是利用A,P,B縱坐標的關系,橫坐標可以嗎?)
由題意可知k≠0,所以k=8,所以直線l的方程為y=8(x-3).
這種解法思路比較自然,利用點斜式,難點在于求解A,B的坐標.但是我們如果直接設A,B的坐標呢?
解 設A(a,2a-2),B(b,-b-3),(因為A,B分別在直線l1,l2上)
因為P為線段AB的中點,所以有
a+b=6
2a-2-b-3=0
所以a=11/3(為什么只要求點A即可)
則A(11/3,16/3),由P(3,o)可知斜率為k=8,所以直線l的方程為y=8(x-3).
這種解法計算過程比較簡單,回避了聯立方程組求解的過程.從直線的構成要素(點)出發,直接設點,然后利用中點求解,方法比較巧妙,
探究 同學們,根據上題,你能否利用初中所學的知識解釋:“當P為中點時,△ABM的面積最小”?
解釋 過點P任意作一條直線分別交l1,l2于點D,E,過點B作/.的平行線交直線DE于點F1,l1,l2交于點M,下面證明S△ABM<△SDEM.
由S△ABM—S四邊形DPBM+SAPD
=S四邊形DPBM+S△PPFB
=S四邊形DFBM,
知S△DEM一S△SABM>0,結論成立.endprint

