不同飽和含水率下路塹土質邊坡流固耦合穩定性分析

摘要：土質邊坡飽水狀態是一種極限狀態，也是邊坡最不穩定狀態。為了解不同飽和含水率對土質路塹邊坡穩定性的影響，文章利用有限差分軟件FLAC 3D建立不同飽和含水率的邊坡數值仿真模型，基于流固耦合理論對邊坡孔隙水壓力、剪切應變增量、安全系數展開分析。研究表明：隨邊坡飽和含水率增大，邊坡孔隙水壓力由地表往深部呈線性增大趨勢；邊坡剪切應變增量增加則滑坡可能性提高，飽和含水率達某特定值，其穩定性不再明顯變化；邊坡安全系數降低，飽和含水率為18.9%時的邊坡失穩，含水率＞18.9%后，流固耦合效應不再明顯。

關鍵詞：邊坡穩定；飽和含水率；流固耦合；土質邊坡；數值模擬

中文分類號：U416.1+4A250794

0引言

邊坡穩定性是公路建設過程中需重點關注的問題之一，其不僅影響施工穩定性，對行車安全亦有顯著影響［1］。安全系數常應用于評價邊坡穩定性。邊坡安全系數在強度折減理論的基礎上發展，從單一折減系數發展至雙折減系數法，乃至于今后的多強度折減法［2］。非飽和、飽和狀態是土石邊坡存在的兩種自然狀態，非飽和是常態工況而飽和狀態為非正常工況。邊坡自然排水在暴雨影響下已達不到排洪要求，使土石邊坡內部的土質含水率迅速升高，最終達到飽和狀態。雨水不能及時排出，在邊坡內部積蓄，導致邊坡穩定性面臨巨大挑戰［3］。非飽和、飽和邊坡穩定性求解方法不斷優化，傳統邊坡分析法將巖土體重度視為常數，比如水位線上方、下方分別采用非飽和、飽和重度，飽和狀態的巖土體重度計算方法未發生過改變，而非飽和重度與飽和度、基底吸力關系密切且呈非線性關聯［4］。邊坡穩定性分析方法主要分為極限平衡法、有限元應力法。在條分法的基礎上，利用極限平衡法求解的每一個土體安全系數均相等，而有限元分析的每個單元體安全系數均有所不同［5］。近年來，眾多學者對非飽和、飽和-非飽和等類型的邊坡穩定性展開了分析研究，如趙永清等［6］針對砂土邊坡于雨后發生失穩或滑坡等現象，基于土力學原理并假定砂土處于飽水狀態，進而利用極限平衡法求解出邊坡安全系數；董建軍等［7］將基質吸力分量、抗剪強度、滲流公式引入至非飽和-飽和滲流理論中，求解得出應力-滲流耦合影響下的邊坡穩定性；張占輝［8］發現降雨、地下水滲流是影響邊坡破壞的主要因素，降雨導致地下水發生滲流，同時引起邊坡孔隙水壓力、應力重分布，邊坡安全系數呈下降變化；張珊［9］利用試驗所得實際土質物理力學性質參數，以有限差分法對不同含水率的土質邊坡安全系數進行求解。

以往研究多為分析非飽和、飽和-非飽和工況下的土質邊坡穩定性，更多從滲流-應力耦合、滑動機理角度切入，但實際當中只需把控最不利情況即可確保邊坡不受破壞。基于此，本文在公路路塹土質邊坡全部處于飽水狀態的背景下，以流固耦合理論為基礎，利用有限差分法對不同飽和含水率工況的邊坡穩定性展開分析，以孔隙水壓力分布規律、剪切應變增量（滑動面）、邊坡安全系數等對邊坡穩定性進行評價分析。

1工程概況

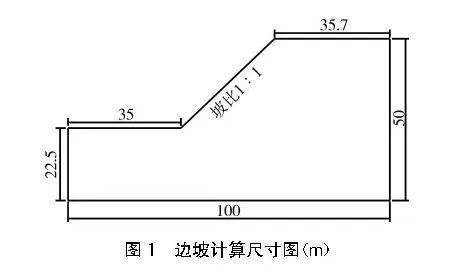
該擬建公路路塹邊坡由殘積土組成，土體性質為砂質黏土，邊坡高27.5 m。超高邊坡工程經風險總體評估后，需對其進行穩定性分析，為后續防護工程設計打下基礎。邊坡計算尺寸具體見圖1，其干密度為1.85 g/cm3，現場取樣測得區域內土體飽和含水率分布范圍為10.8%～21.6%，滲透率為1.32×10-7 m/s，彈性模量為40 MPa，泊松比為0.25，粘聚力為26 kPa，內摩擦角為30°。

2有限差分法模型

由于降雨、地下水、自然蒸發等自然因素的影響，邊坡含水狀態會經歷循環過程，包括干燥狀態、非飽和狀態、飽和狀態。基于流固理論，可知土體力學效應與滲流效應相互影響，邊坡含水量循環變化可使土體孔隙比發生變化。為進一步研究處于不同飽和含水率條件下的邊坡穩定性，在力學邊界的基礎上考慮滲流邊界。力學邊界：底部設置豎向位移約束，側面建立水平位移限制，表面為自由邊界；滲流邊界：土體處于飽水狀態，側面、下部為不透水邊界，表面為零水壓邊界。利用邁達斯軟件進行前處理，通過接口轉化為FLAC 3D網格數據，利用有限差分軟件強大后處理功能進行數值模擬。計算單元為混合網格單元，節點數、單元數分別為7 540個、3 630個。數值分析采用Mohr-Coulomb屈服準則，網格劃分見圖2。數值模擬工況為飽和含水率為0（干燥狀態）、10.8%、13.5%、16.2%、18.9%、21.6%等六種工況，需采用流固耦合分析求解孔隙水壓力場。

3邊坡流固耦合穩定性分析

邊坡流固耦合分析中，滲流模式開啟后并不能直接求解安全系數。鑒于此，開啟滲流模式求解邊坡孔隙水壓力場以及剪切應變增量（滑動面），關閉滲流模式，調用命令“model factor-of-safety associated”求解不同工況的邊坡安全系數，再用“model factor-of-safety list”調出邊坡安全系數。以孔隙水水壓力描述邊坡處于不同工況下的滲流場分布情況，以剪切應變增量判別邊坡潛在滑動趨勢，以邊坡安全系數評價邊坡穩定性。

3.1孔隙水壓力分析

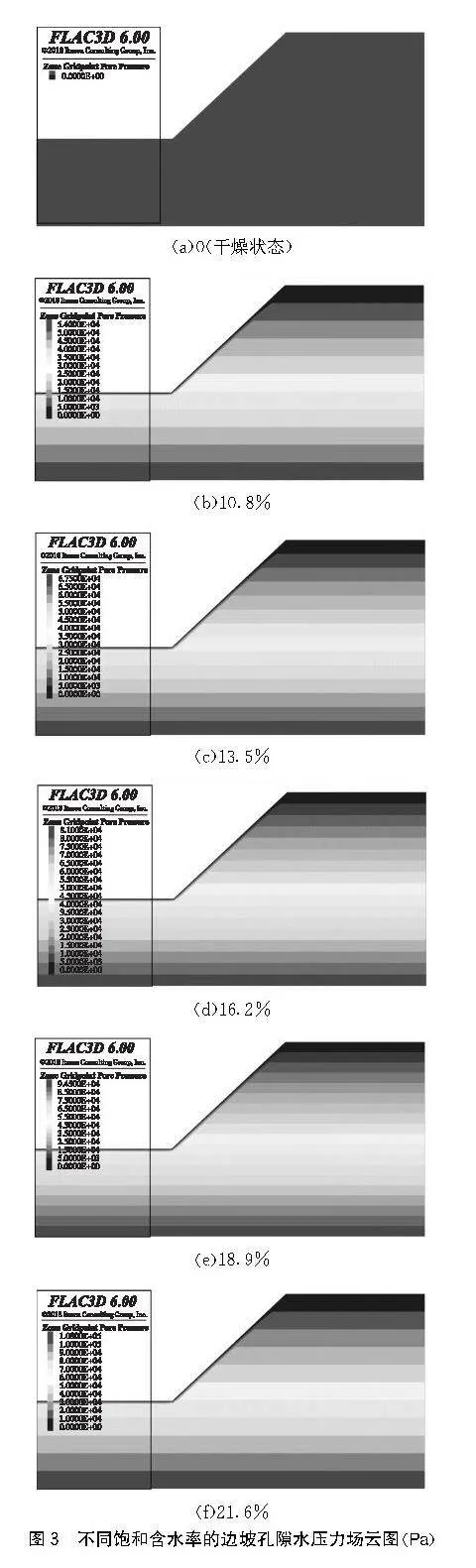
飽水狀態下，邊坡裂隙、孔隙、空隙內充滿水，由于模擬介質為連續介質，水、土在以往數值模擬中求解模式有所不同，而流固耦合分析則將兩者分析整體化，體現了滲流-應力耦合效應。不同飽和含水率邊坡初始孔隙水壓力場見圖3，可看出孔隙水壓力場從上往下依次增大，且飽和狀態下未出現負孔壓。

分析圖3中不同飽和含水率的邊坡孔隙水壓力分布規律，可以得出：

（1）不同飽和含水率的邊坡孔隙水壓力均呈從下往上逐漸降低的趨勢，孔隙水壓力峰值處于邊坡底部，飽水狀態的邊坡處于最不利狀態。形成此情況的原因是因為邊坡防排水未設置完善，造成邊坡整體匯水且并未向外排出，地表水逐漸向下進行滲流，使得浸潤線向下移動，進而導致邊坡下部含水量急速升高且土體性質劣化。

（2）考慮到邊坡經歷降雨、蒸發、土體裂化等影響，土體飽和含水率會發生變化，將土體視為連續介質，邊坡整體飽和含水率一致。邊坡表面孔隙水壓力為零，底部孔隙水壓力為最大值，邊坡各計算單元的孔隙水壓力隨飽和含水率的增大呈線性增大變化，增大速率分別為1 080、350、1 620、1 890、2 160，與飽和含水率相對應。

3.2剪切應變增量分析

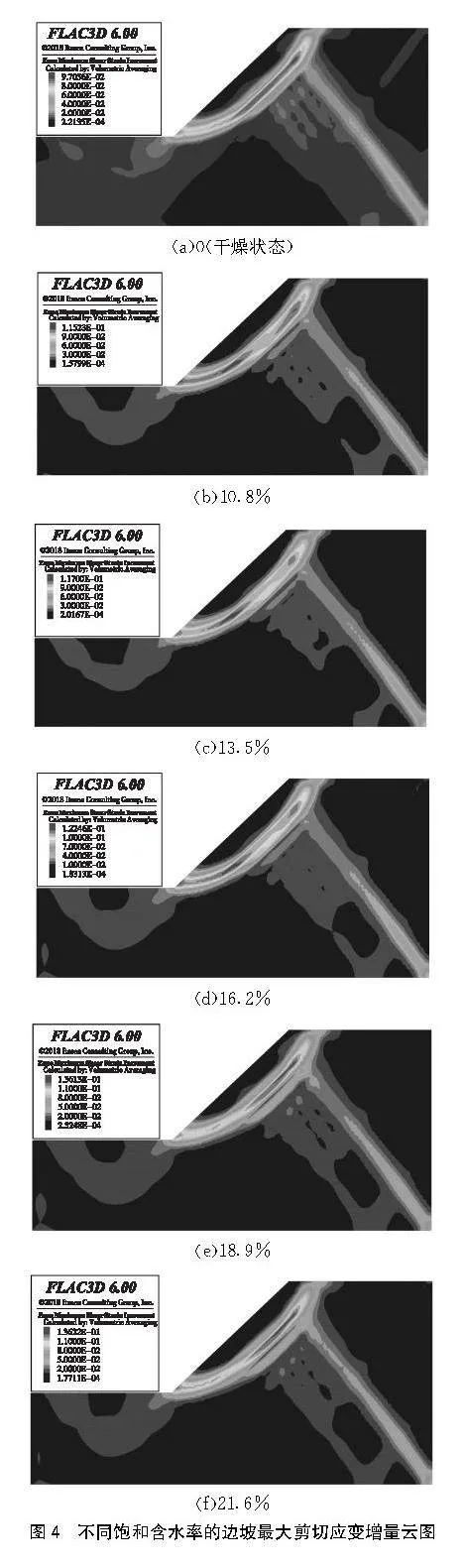
邊坡應變增量既可有效反映出邊坡的位移趨勢，在FLAC 3D軟件中也可借助內置計算公式求解出應力增量、總應力，因此分析邊坡應變增量是十分有必要的。應變增量類型中的最大剪切應變增量可直觀反映出邊坡潛在滑動趨勢與塑性區分布規律。圖4為不同飽和含水率的邊坡最大剪切應變增量分布云圖，可明顯看出邊坡滑動面與塑性區貫通情況。

分析圖4中不同飽和含水率的邊坡最大剪切應變增量分布特征得出：

（1）邊坡最大剪切應變增量反映出不同飽和含水率的邊坡潛在滑動面，圖中白色區域即為潛在滑動面，剪切應變增量峰值大概位于坡腳、坡頂中間處。隨著飽和含水率逐漸增大，邊坡潛在滑動范圍更加明顯且剪切應變增量也隨之增大，結合孔隙水壓力分布規律，進一步說明邊坡處于不同飽和含水率條件下的流固耦合效應有所不同，滲流場與應力場相互影響，使得剪切應變增量也發生改變，從而導致邊坡潛在滑動可能性隨飽和含水率升高而逐漸提高。

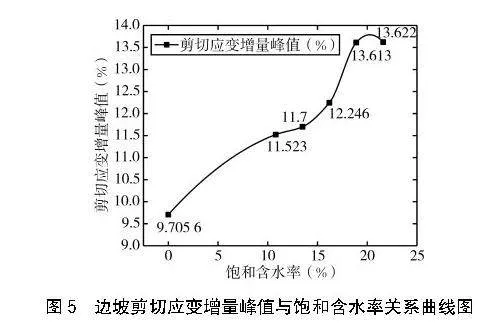
（2）提取圖4的剪切應變增量峰值進行分析，其變化規律見下頁圖5。剪切應變增量隨飽和含水率增加而增加，邊坡由干燥過渡至飽水狀態，剪切應變增量發生突變，說明滲流場對應變場存在明顯影響。在飽和含水率為10.8%～16.2%時，剪切應變增量峰值變化緩慢；飽和含水率從16.2%變化為18.9%時，剪切應變增量峰值再次發生突變，而后趨于平緩。總結剪切應變增量峰值與飽和含水率關系，預測當飽和含水率增加至某一特定值后，剪切應變增量峰值不再明顯增加，說明飽和含水率對潛在滑動面的影響存在一定局限，含水率超過一定范圍，對邊坡穩定性再無顯著影響。

3.3邊坡安全系數分析

基于“二分法”理論，有限差分軟件FLAC 3D利用強度折減法求解邊坡安全系數，通過不斷減小土體的粘聚力、內摩擦角得以實現，進而求解得出不同飽和含水率的邊坡安全系數。以安全系數K=1作為邊坡穩定性評價標準，邊坡安全系數與飽和含水率關系曲線見下頁圖6，強度折減法計算過程見式（1）［10］：

[HL（1：1，Z]cf=cf

φf=arctan[JB（（]tanφf[JB））][HL）]（1）

式中：cf——折減后粘聚力（Pa）；

φf——折減后內摩擦角（°）。

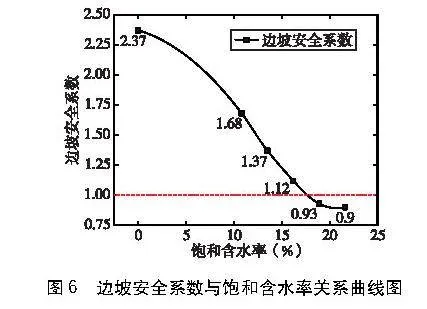
分析圖6中的不同飽和含水率的邊坡安全系數變化規律，可以得出：

（1）不同飽和含水率的邊坡安全系數存在顯著差異，表明不同飽和含水率的邊坡穩定性有所不同。隨著飽和含水率逐漸增加，邊坡安全系數隨之降低；邊坡干燥狀態的安全系數為2.37，說明穩定性良好，由干燥變為飽水狀態，安全系數發生突變；以安全系數K=1作為邊坡穩定性評價標準，得出當飽和含水率增大至18.9%時，安全系數降至0.93，此刻邊坡發生破壞失穩，之后飽和含水率持續增大，邊坡亦發生失穩。

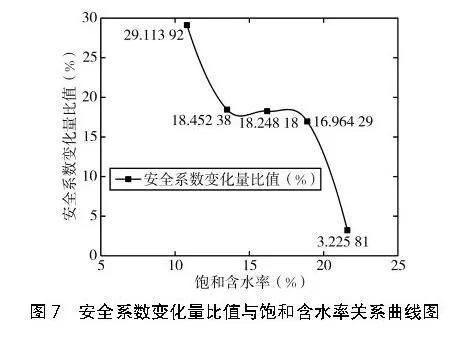
（2）分析圖6的邊坡安全系數變化量比值，得出安全系數變化量比值與飽和含水率的關系曲線（見圖7）。邊坡安全系數變化量比值發生突變在于兩個階段：第一突變階段為干燥狀態變為飽水狀態，邊坡安全系數發生突變（峰值），說明飽和狀態下邊坡流固耦合效應對穩定性的影響顯著；第二突變階段為飽和含水率由18.9%增大為21.6%，安全系數趨于穩定，邊坡已發生失穩破壞，繼續增大飽和含水率對安全系數影響較小，也說明了飽和含水率＞18.9%后，流固耦合效應對邊坡穩定性影響不再顯著。

4結語

本文以某擬建公路路塹邊坡作為背景進行分析，基于流固耦合分析，考慮最不利情況（邊坡整體飽水狀態），構建干燥狀態、不同飽和含水率的邊坡流固耦合模型，利用有限差分法對孔隙水壓力分布規律、剪切應變增量（潛在滑動面）、邊坡安全系數進行分析研究，以安全系數對不同飽和含水率的邊坡穩定性作出評價，得出以下觀點：

（1）孔隙水壓力由地表往深部土體呈逐漸增大趨勢，邊坡自然排水較差造成匯水，地表水向下滲流，同時浸潤線向深部移動，導致下部土體逐漸過渡至飽水狀態，力學性質劣化；邊坡各計算單元的孔隙水壓力隨飽和含水率的增大呈線性增大趨勢，地表水向深部土體滲流對邊坡孔隙水壓力場影響顯著。

（2）隨著飽和含水率增大，邊坡潛在滑動面更加明顯，滲流場與應力場相互影響導致剪切應變增量發生明顯變化，同時滑坡可能性也逐漸提高；剪切應變增量隨飽和含水率增加而增加，干燥變化為飽水的剪切應變增量發生突變，滲流場對應變場存在明顯影響；預測飽和含水率達某特定值時，其剪切應變增量不再增加，同時邊坡穩定性不再顯著變化。

（3）不同飽和含水率的邊坡穩定性有所不同。邊坡安全系數隨飽和含水率增加而降低，飽和含水率增大至18.9%時，邊坡發生失穩破壞；安全系數于干燥狀態變為飽水狀態時發生突變，邊坡流固耦合效應對穩定性影響顯著；當邊坡飽和含水率＞18.9%后，流固耦合效應對邊坡穩定性影響不再顯著。

參考文獻：

［1］劉洋銘，李順興，張亮峰，等.地下水位變化對公路路堤邊坡穩定性及施工成本的影響分析［J］.西部交通科技，2022（12）：57-60.

［2］武博強，李博.基于雙強度折減幅值加權法的公路邊坡穩定性研究［J］.公路交通科技，2023，40（9）：75-81，90.

［3］鄭厚國，周永強，劉燁.高水頭作用下飽和邊坡破壞物質點法模擬研究［J］.能源與環保，2023，45（5）：276-283，288.

［4］詹偉，孫長昊，蘭澤華，等.非飽和土質邊坡安全穩定影響因素研究［J］.甘肅科學學報，2023，35（5）：71-77.

［5］張曉亮.基于極限平衡法和有限元法的邊坡穩定性研究［D］.石家莊：石家莊鐵道大學，2019.

［6］趙永清，李和志，張潔.飽和砂性土邊坡穩定性研究［J］.山西建筑，2020，46（5）：46-48.

［7］董建軍，王思萌，楊曉蕭，等.基于非飽和-飽和滲流的降雨入滲邊坡穩定性分析［J］.水利與建筑工程學報，2018，16（6）：99-104.

［8］張占輝.基于有限元地下水對邊坡穩定性影響分析［J］.地下水，2023，45（5）：97-98.

［9］張珊.不同含水率下非飽和土邊坡的安全穩定性分析［D］.石家莊：石家莊鐵道大學，2018.

［10］巨宏偉.有限元強度折減法在邊坡穩定性分析中的應用［J］.市政技術，2023，41（3）：122-128.

作者簡介：甘霖（1975—），工程師，主要從事道路工程方向研究工作。