利用三參數AVO近似方程的深層疊前地震反演

印興耀 王慧欣 曹丹平 周琦杰 郭淑文

(①中國石油大學(華東)地球科學與技術學院，山東青島 266580； ②中國石化上海海洋油氣分公司勘探開發研究院，上海 200120； ③中國石油大港油田勘探開發研究院，天津 300280)

1 引言

隨著油氣勘探領域、深度的擴展，深層油氣勘探已成為地球物理勘探的重點，因而深層油氣儲層的疊前地震反演和流體識別方法成為研究熱點。由于受埋藏深度的影響，深層儲層地震資料往往表現出入射角范圍窄、照明度不足、信噪比和分辨率較低、阻抗差異小、AVO反射特征不明顯等特征，給地震反演(尤其是疊前反演)帶來了新的挑戰。針對深層儲層資料的這些特征及儲層流體識別的難題，印興耀等[1]和劉曉晶等[2]分別采用對深層儲層較為敏感的Russell因子和Gassmann流體項，對埋藏較深的構造—巖性復合圈閉及以深水砂礫巖為主導的隱蔽油氣藏進行流體識別，都取得了較好應用效果，但Russell和Gassmann等流體因子易受孔隙度等因素影響而產生流體識別的假象。

Yin等[3]基于孔隙介質理論，依據臨界孔隙度模型和突出流體體積模量Kf的Gassmann流體項經驗公式推導出基于流體體積模量Kf、固體剛性參數fm、密度ρ和孔隙度φ的四參數AVO近似式。與常規流體因子相比，流體體積模量Kf只與流體有關而不受孔隙度影響，減少了流體識別的假象，顯著提高了流體識別的可靠性。雖然該方法已取得較好效果，但在實際應用中仍存在一定局限性： ①該近似式的反射系數之間并不是完全獨立的； ②該方法需要四個角道集。

針對上述問題，本文根據深層地震資料入射角范圍較窄和常規流體因子敏感性較低的特點，沿用了對儲層較為敏感的流體體積模量Kf[3]，基于Xu-White模型和巖石物理統計特征，厘清了固體剛性參數fm與孔隙度φ之間的指數關系，并推導出流體體積模量Kf、固體剛性參數fm和密度ρ的三參數AVO近似方程。模型和實際資料的應用結果表明本文提出的近似方程在窄角度情況下的精度和穩定性均滿足反演的要求，而且在應用中具有現實的可行性。

2 Kf-fm-ρ三參數AVO近似方程和反演

2.1 Kf-fm-ρ三參數AVO近似方程推導

Gassmann流體項f作為儲層流體識別的重要參數，在目前的實際應用中已取得較好效果，但本身受流體和固體骨架雙重作用，易受骨架和孔隙度等參數影響而形成流體識別假象。當采用流體體積模量Kf作為流體因子進行流體識別時可對固體骨架影響和流體效應進行解耦，因此在指示流體性質方面具一定優勢。

Yin等[3]參考Nur等[4]、Batzle等[5]和Han等[6]巖石物理的研究成果，推導出基于流體體積模量的Kf-fm-ρ-φ四參數AVO近似方程

(1)

式中：γdry是干巖石縱橫波速度比；γsat是飽和巖石縱橫波速度比；Kf為流體體積模量；fm=φμ,為固體剛性參數，其中φ為孔隙度，μ為剪切模量；ρ為密度。

式(1)中包含的固體剛性參數fm與孔隙度φ之間存在關系fm=φμ，因此該反射系數之間并不是完全獨立的； 其次，該方法需要四個角道集，反演條件數也隨之增加，導致穩定性降低； 另外，對于入射角范圍較窄的深層儲層而言，在有限角度信息中提取四個具有一定差異且可用于反演的角道集是較困難的，因此該方法并不適用于窄角度深層儲層。所以本文在式(1)基礎上，根據Xu-White模型，推導出基于流體體積模量Kf、固體剛性參數fm和密度ρ的三參數AVO近似方程，其中流體體積模量Kf可通過彈性阻抗反演穩定地提取并應用于深層儲層的流體識別。

剪切模量μ主要與骨架、骨架礦物和孔隙度有關，受含水飽和度和流體的影響比較小。圖1是基于Xu-White模型，泥質含量(SH)從40%變化到100%，φ從10%變化到30%時，φ與μ的關系圖。經過大量實際資料的交會分析，得知φ與μ之間具有一定的指數關系。圖2是中國東部某實際工區的φ與μ的巖石物理交會圖。根據圖1和圖2中的巖石物理關系特征圖，可建立φ與μ之間的指數關系。

圖1 不同泥質含量時孔隙度φ與剪切模量μ的關系

圖2 實際工區孔隙度φ與剪切模量μ的交會圖

根據實際工區特點和巖石物理統計規律，建立φ與μ之間的指數關系

μ=aφα

(2)

據前述關系式，得到

fm=μφ=aφαφ=aφ1+α

(3)

令1+α=r，有

fm=aφr

(4)

式(2)～式(3)中a和r是根據實際工區特點建立的有關φ與μ之間的擬合系數。

(5)

將式(5)代入式(1)可得到基于Kf、fm和ρ的三參數AVO近似方程

(6)

2.2 Kf-fm-ρ三參數AVO近似方程精度分析

為了對式(6)進行精度檢驗，設計模型參數如表1的深層砂巖模型，其上覆地層是含氣砂巖，下伏地層是含水砂巖。分別用精確Zoeppritz方程、式(1)和式(6)計算得到地層界面處反射系數(圖3)。

從圖3可看出當入射角較小時，式(6)與Zoep-pritz方程的精度相當，反射系數曲線幾乎重合，而且其精度高于由式(1)得到的反射系數，但隨著角度的增加，誤差逐漸增大。模型精度分析表明式(6)滿足深層儲層反演對精度的要求。

表1 深層砂巖模型參數

圖3 深層含氣砂巖模型反射系數對比圖

參考Connolly[7]和Whitcombe[8]提出的彈性阻抗以及標準化的概念，推導出有關流體體積模量Kf的三參數標準化彈性阻抗公式

(7)

其中

(8)

對式(7)取自然對數，并將其進行線性化變換

(9)

對于一道有n個采樣點的地震數據，可構建如下矩陣

(10)

分別將三個角度的彈性阻抗和井旁道數據代入式(10)中，可以得到三個角度對應的九個系數a(θi)、b(θi)、c(θi)(其中i=1，2，3)，將此九個系數代入下列方程組中

(11)

可得流體體積模量、固體剛性參數和密度。

2.3 三參數AVO近似式信息量分析

在AVO近似公式中不同的彈性參數所對應的反射系數的信息比重有所不同，因此不同的彈性參數的反演可靠性也存在一定的差異。為了研究利用式(6)反演彈性參數的可行性，采用Nicolao等[9]提出的信息敏感分析方法，定量分析式(6)中的彈性參數的信息敏感性。

將式(6)以如下形式表示

R(θ)=G(θ)m

(13)

式中

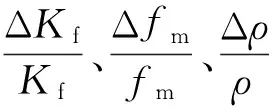
圖4 模型空間中的三個特征值(a)及特征向量方向余弦(b)隨最大入射角度的變化曲線

2.4 三參數AVO近似式穩定性分析

穩定性對反演(尤其是當數據不夠完備時)非常重要。圖5是相同條件下基于式(1)和式(6)系數矩陣的條件數的常用對數對比。當最大入射角從20°增大到30°時，兩個條件數都有減小的趨勢，但基于式(1)系數矩陣的條件數都明顯大于式(6)，表明隨著最大入射角的增加，基于Kf的四參數和三參數AVO近似方程的穩定性都隨之提高，但后者的穩定性明顯高于前者。

圖5 基于式(6)和式(1)系數矩陣條件數分析

精度分析表明，當入射角較小時，式(6)與Zoeppritz方程精度相當； 穩定性分析表明式(6)的穩定性明顯高于式(1)，因此式(6)滿足反演的精度和穩定性要求。

3 模型試算

首先通過實際井資料計算得到Kf、fm和ρ的測井曲線，利用上述井數據與35Hz雷克子波進行褶積得到CMP道集，再通過合理的角度部分疊加得到三個角度(5°，15°，25°)部分疊加道集，最后利用式(6)進行彈性阻抗反演。圖6是在無噪和信噪比SNR=2∶1情況下，通過彈性阻抗反演得到的Kf、fm和ρ曲線。圖7是無噪和SNR=2∶1時提取的Kf和ρ的相對誤差。可見在無噪時Kf、fm和ρ的反演結果與模型數據幾乎重合，相對誤差都較小； 當SNR=2∶1時，Kf的反演結果受到一定影響，其總體趨勢仍與模型數據基本吻合，但fm和ρ的反演結果較差，相對誤差也明顯增大； 另外，這兩種情況下，Kf反演結果的相對誤差(集中分布在8%附近)都小于ρ。由于fm=φμ，實際測井數據中孔隙度φ信息含量十分匱乏； 密度項反演結果較差，原因是由于密度項的量綱遠小于其他兩項，而且變化不夠明顯，導致反射系數的信息量相對較小。模型測試結果表明： 本文方法在反演過程中具有較好的抗噪性，可有效地提取流體體積模量參數，從而為深層儲層流體識別提供了較為可靠的數據支撐。

圖6 無噪(左)和SNR=2∶1(右)時的三參數反演結果 黑色實線為模型數據，紅色虛線為反演結果

圖7 無噪(左)和SNR=2∶1(右)時提取的Kf和ρ的相對誤差統計

4 實際資料應用

將本文的彈性阻抗反演方法應用于中國東部陸上M深層油田，其目的儲層埋深達4500m，對應時間約為3s，最大入射角是24°，只提取到三個(5°、15°、25°)可用于反演的角度道集，物性數據較差，地震資料入射角范圍較窄。利用巖石物理交會圖(圖8)和Dillion等[10]提出的流體因子敏感性定量分析方法對該工區測井資料進行比較分析，發現流體體積模量Kf對目的層最為敏感(圖9)。

將疊前CMP道集轉換到角度域后，進行角度部分疊加得到三個角度部分疊加剖面，再利用本文疊前彈性阻抗方法進行反演，提取到流體因子Kf和密度ρ剖面(圖10，插入的測井解釋柱狀圖中紅色代表油層、粉色代表水層)。在Kf的反演結果與測井解釋結果吻合較好，油層出現明顯的偏小趨勢，可區分油層和水層(圖10a)； 在ρ的反演結果中油層與水層數值差別較小，難以區分油層和水層(圖10b)。因此，本文提出的利用彈性阻抗提取流體體積模量Kf方法在實際應用中具有現實性和可靠性，在深層儲層的流體識別中具有明顯優勢。

圖8 流體體積模量與固體剛性參數交會圖

圖9 流體敏感性分析

圖10 流體體積模量(a)和密度(b)反演剖面

5 結論

(1)本文在Xu-White模型基礎上，根據巖石物理特征以及實際工區統計規律，推導出了針對深層窄角度的基于流體體積模量Kf、固體剛性參數fm和密度ρ的三參數AVO近似方程及彈性阻抗方程；

(2)Kf-fm-ρ三參數AVO近似方程只需要三個角度疊前地震數據，且三參數反射系數之間相關性較低；

(3)Kf-fm-ρ三參數AVO近似方程與精確Zoeppritz方程的精度相當，誤差較小，而且其條件數也明顯小于Kf-fm-ρ-φ四參數AVO近似方程，因此本文所述方法能滿足反演對精度和穩定性的要求；

(4)Kf作為流體因子，在進行流體識別時對目的層的敏感度較高；

(5)模型測試和實際資料應用表明三參數AVO近似方程及其彈性阻抗方程在針對窄角度的深層儲層進行流體識別時，具有較好的穩定性和實用性。

本文所述方法仍具有一定局限性，它不適用于低孔隙度的致密儲層，這是由于式(1)在推導過程中主要引用了Nur等[4]的臨界孔隙度模型和Han等[6]的巖石物理統計規律，這些理論都是基于孔隙度較大情況下提出的，因此本文的方法更適用于孔隙度相對較大的深層儲層。

[1] 印興耀，張世鑫，張峰.針對深層流體識別的兩項彈性阻抗反演與Russell流體因子直接估算方法研究.地球物理學報，2013，56(7)：2378-2390. Yin Xingyao，Zhang Shixin，Zhang Feng.Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification.Chinese Journal of Geophysics，2013，56(7)：2378-2390.

[2] 劉曉晶，印興耀，吳國忱等.基于基追蹤彈性阻抗反演的深部儲層流體識別方法.地球物理學報，2016，59(1)：277-286. Liu Xiaojing，Yin Xingyao，Wu Guochen et al.Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance.Chinese Journal of Geophysics，2016，59(1)：277-286.

[3] Yin Xingyao and Zhang Shixin.Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation.Geophysics，2014，79(5)：R221-R232.

[4] Nur A，Mavko G，Dvorkin J et al.Critical porosity：A key to relating physical properties to porosity in rocks.The Leading Edge，1998，17(3)：357-362.

[5] Batzle M，Hofmann R，Han D H et al.Fluids and frequency dependent seismic velocity of rocks.The Leading Edge，2001，20(2)：168-171.

[6] Han Dehua and Batzle M L.Gassmann’s equation and fluid-saturation effects on seismic velocities.Geophysics，2004，69(2)：398-405.

[7] Connolly P.Elastic impedance.The Leading Edge，1999，18(4)：438-452.

[8] Whitcombe D N.Elastic impedance normalization.Geo-physics，2002，67(1)：60-62.

[9] Nicolao A D，Drufuca G，Rocca F.Eigen values and eigenvectors of linearized elastic inversion.Geophy-sics，1993，58(5)：670-679.

[10] Dillon L，Schwedersky G，Vásquez G et al.A multi-scale DHI elastic attributes evaluation.The Leading Edge，2003，22(10)：1024-1029.

[11] 印興耀，李超，張世鑫.基于雙相介質的地震流體識別.中國石油大學學報(自然科學版)，2013，37(5)：38-43. Yin Xingyao，Li Chao，Zhang Shixin.Seismic fluid discrimination based on two-phase media theory.Journal of China University of Petroleum (Edition of Natural Science)，2013，37(5)：38-43.

[12] 印興耀，曹丹平，王保麗等.基于疊前地震反演的流體識別方法研究進展.石油地球物理勘探，2014，49(1)：22-34，46. Yin Xinygao，Cao Danping，Wang Baoli et al.Research progress of fluid discrimination with pre-stack seismic inversion.OGP，2014，49(1)：22-34，46.

[13] 印興耀，宗兆云，吳國忱.巖石物理驅動下地震流體識別研究.中國科學：地球科學，2015，01：8-21. Yin Xingyao，Zong Zhaoyun，Wu Guochen.Research on seismic fluid identification driven by rock physics.Science China Earch Sciences，2015，58：159-171.

[14] 印興耀，劉欣欣.儲層地震巖石物理建模研究現狀與進展.石油物探，2016，55(3)：309-325. Yin Xingyao，Liu Xinxin.Research status and progress of the seismic rock-physics modeling methods.GPP，2016，55(3)：309-325.

[15] Russell B H，Gray D，Hampson D P.Linearized AVO and poroelasticity.Geophysics，2011，76(3)：C19-C29.

[16] Shuey R.A simplification of the Zoeppritz equations.Geophysics，1985，50(4)：609-614.

[17] Smith G，Gidlow P.Weighted stacking for rock property estimation and detection of gas.Geophysical Prospecting，1987，35(9)：993-1014.

[18] Quakenbush M，Shang B，Tuttle C.Poisson impedance.The Leading Edge，2006，25(2)：128-138.

[19] Gray D.Elastic inversion for Lamé parameters.SEG Technical Program Expanded Abstracts，2002，21.

[20] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solidⅡ:Higher frequency range.Journal of the Acoustical Society of America，1956，28(2)：179-191.

[21] Russell B H，Hedlin K，Hilterman F J et al.Fluid-

property discrimination with AVO：A Biot-Gassmann perspective.Geophysics，2003，68(1)：29-39.

[22] Russell B H，Gray D，Hampson D P et al.Linearized AVO and poroelasticity.CREWES Research report，2006，18：1-25.

[23] 鄧煒，印興耀，宗兆云.等效流體體積模量直接反演的流體識別方法.石油地球物理勘探，2017，52(2)：315-325. Deng wei，Yin Xingyao，Zong Zhaoyun.Fluid identification based on direct inversion of equivalent fluid bulk modulus.OGP，2017，52(2)：315-325.

[24] 印興耀，張世鑫，張繁昌等.利用基于Russell近似的彈性波阻抗反演進行儲層描述和流體識別.石油地球物理勘探，2010，45(3)：373-380. Yin Xingyao，Zhang Shixin，Zhang Fanchang et al.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification.OGP，2010，45(3)：373-380.

[25] 鄭笑雪，杜啟振，孟憲軍等.橫向約束分步疊前彈性參數反演.石油地球物理勘探，2017，52(4)：760-769. Zheng Xiaoxue,Du Qizhen,Meng Xianjun et al.Lateral constraint two-step prestack elastic parameter inversion.OGP，2017，52(4)：760-769.