老師,這道題的數(shù)學模型是什么
2018-03-13 18:53:35王思儉
新高考·高三數(shù)學
2017年8期
王思儉


考試結束了,學生涌出考場,邊走邊議論,“今天的應用題,我沒有想到它是什么模型”“我又沒有理解題意,不知道如何建立數(shù)學模型”“題目中的參量較多,不知道選擇哪一個作為自變量”“應用題的數(shù)學模型究竟有哪些,我背了前幾年的數(shù)學模型,但一到考場里就全忘記了,不知道怎樣尋找?guī)讉€量之間的聯(lián)系”……我為此邀請幾位學生針對數(shù)學應用題的建模問題進行交流,旨在通過對幾道應用題的分析,引導學生尋找變量與變量、變量與參量的內(nèi)在聯(lián)系,掌握建立數(shù)學模型的基本思路.
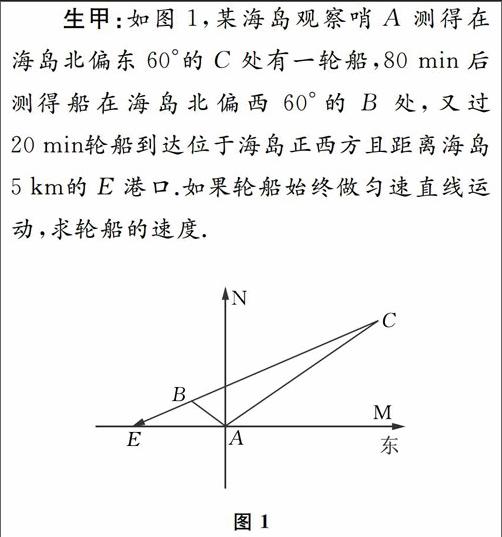
生甲:如圖1,某海島觀察哨A測得在海島北偏東60°的C處有一輪船,80min后測得船在海島北偏西60°的B處,又過20min輪船到達位于海島正西方且距離海島5km的E港口.如果輪船始終做勻速直線運動,求輪船的速度.
我沒有讀懂題意,這題的數(shù)學模型是什么?我建立直角坐標系求解,運算量較大,過程太繁瑣,沒有成功!
師:首先要弄清楚本題有哪些條件,結論要求什么?條件有4個,結論是計算輪船的速度,我們只要計算BE或BC的長.你們知道線段BC與BE所用的時間之比是多少嗎?
眾生:4∶1.
師:于是問題可以轉化為我們要求的線段長度之比是多少?
眾生:也是4∶1.
師:你們再閱讀題目,找一找還有哪些已知條件?
師:很好!本題是以解三角形為背景的應用題,數(shù)學模型就是路程與速度的模型.從解題過程來看,關鍵是要找出或設出角度,實質(zhì)是解斜三角形,將問題涉及的有關量集中在某一個或者幾個三角形中,靈活地運用正弦定理、余弦定理來加以解決.
登錄APP查看全文
猜你喜歡
童話王國·奇妙邏輯推理(2024年5期)2024-06-19 16:03:38
數(shù)學物理學報(2020年2期)2020-06-02 11:29:24
學苑創(chuàng)造·A版(2019年5期)2019-06-17 01:14:21
光學精密工程(2016年6期)2016-11-07 09:07:19
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
核科學與工程(2015年4期)2015-09-26 11:59:03
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
中學生數(shù)理化·高二版(2008年7期)2008-06-15 01:31:20
中學數(shù)學雜志(初中版)(2006年1期)2006-12-29 00:00:00
