基于幾何校正和LT碼的魯棒圖像水印

章無用，陳建華

(云南大學 信息學院，云南 昆明 650500)

0 引 言

魯棒水印算法大致可以分為以下3類：①基于不變域。將水印信息嵌入到對幾何攻擊具有不變性的域。如基于圖像的不變矩[1-3]，將水印嵌入到矩的不變系數上，基于不變矩的算法對簡單的幾何攻擊有一定的魯棒性，而對不等比例縮放、剪切、組合幾何攻擊等魯棒性較差。或者基于圖像的某種變換[4-6]，一般情況下，此類算法魯棒性較強，但是運算比較復雜，且水印嵌入容量較小。②基于圖像特征[7-10]。從圖像中提取出特征點，然后利用特征點構造某種不受幾何形變影響的局部區域，將水印嵌入到這些與載體內容有關的特征區域，水印的檢測也通過這些局部區域實現，此類算法抗攻擊種類較多，缺點是嵌入容量有限。③基于模板校正的算法。利用模板估計幾何形變的參數，然后實施逆變換，重同步并提取水印。Zhang等用Tchebichef矩估計幾何攻擊的參數并進行還原[11]，參數的估計較為精確，但實驗結果表明只能抵抗一些常見的RST攻擊；Lou提出一種基于特征點模板的算法來估計RST攻擊的參數[12]，模板性能較為穩定，對一些簡單的RST攻擊性能較好；Wang等設計了具有幾何不變性的可變形多尺度變換[13]，并基于此變換推導了幾何同步機制，算法復雜度較低，但不能抵抗一般仿射變換等攻擊，且水印提取時要用到原始圖像；Wang等利用模糊支持矢量機(FSVM)估計幾何失真的參數并進行校正[14]，算法嵌入容量大，對于單一的RST攻擊效果較好，但抵抗組合幾何攻擊性能較差，并且不能抵抗一般仿射變換攻擊。

綜上所述，第①類算法不能有效地抵抗剪切、組合幾何攻擊等，第②類算法嵌入容量較小，第③類算法只能抵抗簡單的幾何攻擊，對于剪切、RST的組合攻擊、一般仿射變換攻擊等魯棒性較差。考慮到水印的嵌入容量、嵌入水印后載體圖像的視覺效果以及對不同載體的普遍適用性，利用模板進行幾何校正的方法具有相對較好的性能。同時，鑒于常見的基于模板校正的水印算法抵抗一般仿射變換、組合幾何攻擊性能較差的缺點，本文采用估計仿射變換矩陣并實施逆變換的方法解決此問題，更進一步，恢復幾何形變的圖像行列往往有細微的偏差，本文算法在空間域嵌入一層水印對變換域的版權保護水印的邊界進行準確的定位。

本文方案先利用SIFT算法[15]從載體圖像中提取并從中挑選出少量不易受幾何形變影響的特征點作為模板，與受攻擊的圖像提取出的特征點進行匹配，再用RANSAC算法[2]進行挑選，剔除誤匹配的特征點對，然后利用最小二乘法估計出仿射矩陣，對圖像進行仿射逆變換，得到校正的圖像。在經過仿射矩陣校正之后，圖像的尺度還有輕微的偏差，圖像的邊界也遭到了破壞，故而本文算法將版權水印W1嵌在DWT-DCT的混合域，以承受像素的細微偏差，同時還利用奇偶量化法[7]在空間域嵌入定位水印W2，在校正各種幾何形變后，精確定位DWT-DCT域版權水印W1的嵌入起點。最后，從幾何校正圖像的DWT-DCT域中提取出W1。針對大部分水印算法抗剪切攻擊脆弱的狀況，利用LT碼[16]優異的糾刪性能，將版權水印信息W1先經過LT碼編碼，再用失真補償量化索引調制(DCQIM)算法[17]將編碼水印信息嵌入到DWT-DCT混合域中，以達到抗剪切的目的。

1 SIFT特征點的提取和挑選

1.1 SIFT特征點提取

常見的圖像尺度不變特征提取算法主要有Harris-Laplace[18]、SIFT、SURF[19]算法等，相對于Harris-Laplace、SURF算法，Lowe提出的SIFT算法具有更好的旋轉和尺度不變性[20,21]，本文采用SIFT算法進行特征點的提取。其提取特征點的過程主要分為以下幾個部分：①在DoG尺度空間檢測極值，并且確定特征點的尺度和位置；②以Hessian矩陣H作為判斷標準剔除邊緣點和對比度低的點；③給每個特征點分配一個主方向；④SIFT特征向量的生成。

將原始圖像與不同尺度的高斯核卷積便得到一組被平滑圖像的尺度空間，尺度空間中相鄰的圖像相減便得到DoG多尺度空間，如圖1所示，將DoG尺度空間中的每個點跟當前尺度空間周圍的8個點以及相鄰的上下尺度空間中對應位置的周圍鄰域9個點進行比較，僅當被檢測的點的DoG值大于此26個點或小于此26點時，才將該點判定為極值點并保留以進行后續計算。

圖1 DoG尺度空間局部極值檢測

在求出極值點所處的位置和尺度后，利用2×2的Hessian矩陣H去除不穩定的特征點。

對每個特征點，在以其為中心的鄰域窗口內利用直方圖統計鄰域像素的梯度分布，找到直方圖的最高峰值便可確定特征點的主方向。

最后以特征點為中心、以特征點主方向為基準生成一個128維的特征向量。

1.2 特征點的挑選

從圖像提取出幾百甚至上千個特征點之后，首先去除大尺度和小尺度的特征點，因為尺度太大和太小的點在受到幾何攻擊后容易丟失。因此，對從載體圖像中檢測到的特征點，只保留中間尺度范圍的特征點[7,22]。

接著，根據其對應的|DoG|值[7,15]大小，選出其中|DoG|值最大的特征點，設其坐標為(t1,t2)，對應的尺度為σ，生成圓形特征區域如式(1)

(x-t1)2+(y-t2)2=(kσ)2

(1)

然后從剩下的特征點中選出|DoG|值最大，且由式(1)確定的特征區域與之前的區域不重疊的特征點，重復上述操作，根據圖像紋理豐富程度的不同選出20個左右的特征點。同時將這些特征點的特征向量作為密鑰進行保存，用于水印檢測時仿射矩陣的估計。特征點的選擇過程如圖2所示，以圖像Lena為例。

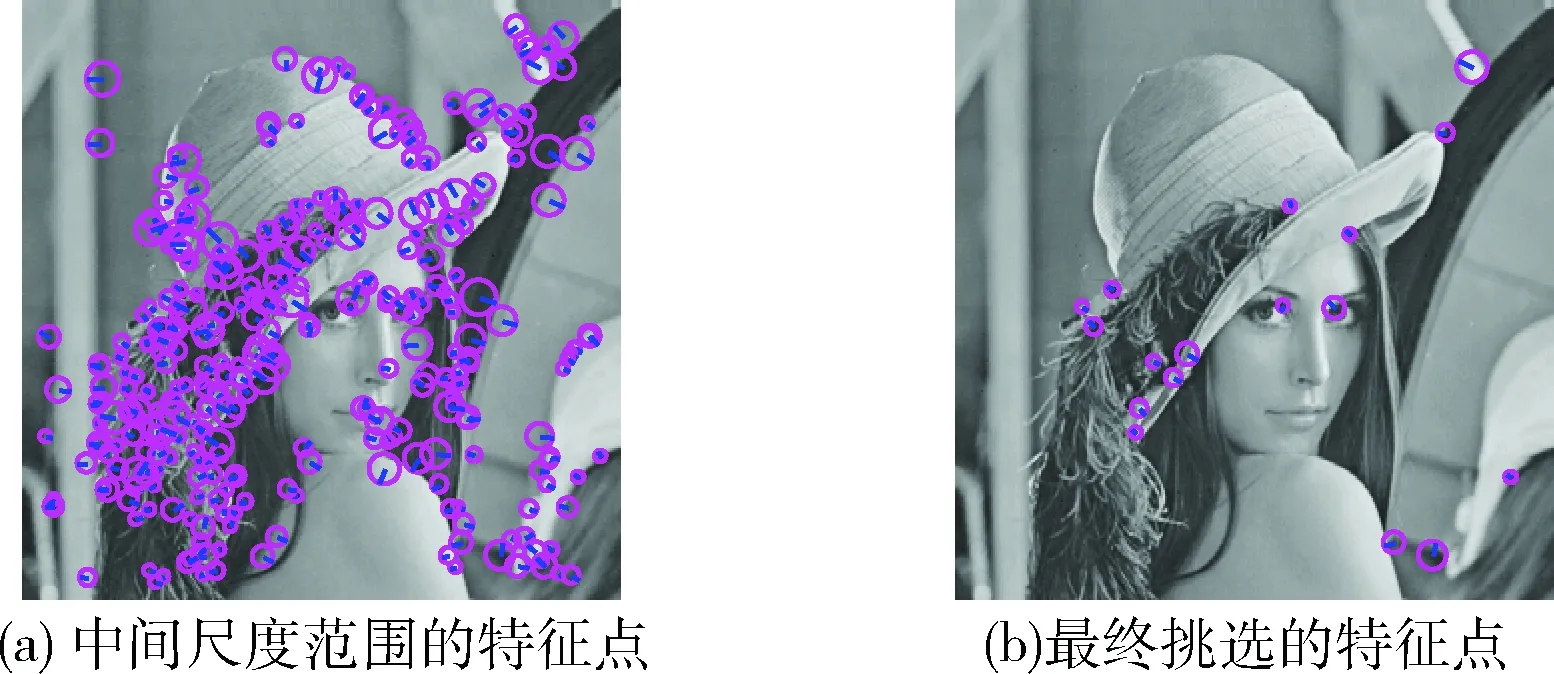
圖2 特征點的挑選

2 幾何攻擊檢測與校正

通常情況下，圖像仿射變換前后的坐標關系如式(2)

(2)

點(u,v)為原始坐標、(x,y)為仿射變換后的坐標，其中仿射矩陣A為

(3)

由于平移系數Tx、Ty不能影響到仿射矩陣A，故而完全可以在求出仿射矩陣A并對受攻擊的圖像進行幾何校正之后，根據校正后圖像的相應特征點與密鑰中特征點之間的對應關系求出Tx、Ty，因此關鍵是根據匹配特征點間的關系求出A。雖然仿射矩陣A隨攻擊順序不同而變化，如式(4)為先旋轉、再縮放、后沿X軸方向錯切、最后沿Y軸方向錯切的過程，但本文采用匹配特征點的關系求A，避免了多數基于模板校正的算法需要判斷攻擊順序，估計旋轉、縮放參數等繁瑣的過程

(4)

在水印的檢測端，利用SIFT算法從受攻擊的載體圖像中提取特征點及相應的特征向量，與密鑰中的原始特征點進行匹配，假設Ωi(i=1,2,…,n1)為從受攻擊圖像提取的特征點，Uj(j=1,2,…,n2)為原始的特征點，則Ωi、Uj的相似度可以用它們相應向量之間的歐氏距離表示，距離越小則特征點的相似度越高，但這樣很可能出現誤匹配，為減小因誤匹配而導致的仿射矩陣估計的誤差，本文采用RANSAC算法[2]對特征點進行挑選，以提高特征點的正確匹配率。RANSAC算法實際操作過程如下：

輸入:少量的原始特征點U,受攻擊圖像提取的特征點Ω,最大的循環次數Cmax,允許的最大誤差εmax。輸出:N2組匹配誤差較小的特征點對。for i=1 to Cmax do 從U,Ω隨機選擇3組匹配的特征點對求得仿射矩陣A1,并令N1=0; for allP∈U do //P為原始特征點 if|Ω(P')-U(P)A1|<εmax then //P'為與P相匹配的特征點 N1=N1+1 endif endfor if N1>N2 //N2的初始值為3 N2←N1 endif endfor

經過RANSAC算法的挑選，基本剔除了誤匹配的點，然而，實際上剩下的匹配的特征點可能本身就存在誤差，本文使用最小二乘法來最小化誤差。構建目標函數為

(5)

3 水印嵌入與提取過程

3.1 版權水印W1的實現

針對現有的一些水印算法，比如常見的基于不變域、模板校正的水印算法抗剪切性能較差的現象，本文先將水印信息W1進行LT碼編碼，編碼后得到比特流W1(b)，b=1,2,3…。

LT碼具有良好的糾刪性能，但并不能檢錯，故而需加入校驗碼，將出錯的LT碼編碼數據包檢測出來并刪除。本文使用檢錯功能較強的CRC碼進行檢錯，在LT編碼數據包后面加入一定長度的CRC碼。

由于幾何攻擊和校正過程破壞了數字圖像的邊緣，增加或減少了一些行和列，為了降低水印W1的誤碼率，W1不嵌到整幅圖像，而是嵌在離邊緣還有一定距離的圖像塊中。因此，先對水印W1嵌入區域進行一級DWT變換，由于低頻子帶LL1集中了主要能量，將水印嵌入到該子帶中將具有很好的魯棒性。然后，對LL1進行8×8的DCT變換，再利用DCQIM算法將水印嵌入到DCT變換塊的中低頻系數中，具體操作流程如下：

(1)在需要嵌入W1編碼比特流的DCT變換塊i中選取8個備選嵌入點，其位置記為j，j=1,2,3,…,8,并將嵌入點的DCT系數[23]記為fi(j)。

(2)在8個備選嵌入點中選擇c(1≤c≤8)個點，作為嵌入的位置。

(3)按照式(6)進行W1編碼比特流的嵌入

(6)

式中：γ為量化補償參數，取值在0～0.25之間[17]，aj為量化步長，表示JPEG標準量化表中與位置為j的嵌入點對應的量化系數，Qm是量化器，其定義如下

(7)

(4)編碼水印信息嵌入后，再進行IDCT、IDWT得到嵌入編碼水印W1的載體圖像。

版權保護水印W1的提取過程如下：

(1)利用空域W2的水印信息搜索幾何校正的圖像，定位W1嵌入起點，過程詳見3.2節，同時截取水印W1嵌入部分。

(2)將嵌入水印W1的部分圖像進行一層DWT,對LL1進行8×8的DCT變換，然后到相應的DCT變換塊系數中，按式(8)提取水印比特流W1(b)′

(8)

其中

(9)

3.2 空間域水印W2的實現

水印W2是利用奇偶量化法嵌入在空間域的3個特定位置，如圖3所示。一個大方塊由若干個小方塊組成，一個小方塊由若干像素構成，每個小方塊嵌入1 bit信息。并且每個小方塊嵌入的水印信息與它周圍的小方塊是相異的，以增強定位的精準性。

圖3 W2嵌入區域

具體的嵌入過程如下：

(1)對所要嵌入區域的每個像素I(x,y)計算量化函數值Q(x,y)，其中Δ表示量化步長

(10)

(2)求出每個像素的量化噪聲δ(x,y)

(11)

(3)確定像素的修改量m(x,y)，使修改后的像素值處于量化區間的中點

(12)

(4)修改后的像素值為I*(x,y)=I(x,y)+m(x,y)， 對區域內的每個像素進行上述操作，得到嵌入水印W2的載體圖像。

W2的提取方法如下：對幾何校正后的圖像進行與嵌入過程相同的方塊分割，然后對每個小方塊內的像素利用式(10)計算量化函數值，并記第i個方塊內函數值為0的像素個數為CNTi,0，函數值為1的像素個數為CNTi,1，通過式(13)提取水印W2′

(13)

(14)

圖4 搜索區域

4 實驗結果與分析

4.1 相關說明

實驗使用的仿真工具為2011b版MATLAB。以嵌入容量、透明性、魯棒性為評價指標。并與文獻[6]、文獻[8]中的算法進行了對比。采用256級512×512的標準灰度圖像Lena、Peppers、Airplane作為測試圖像，如圖5所示，水印W1是480 bits的二值偽隨機序列，LT編碼數據包的長度為1，CRC編碼時，信息位與校驗位長度都是6 bits，每個8×8的DWT-DCT塊嵌入6 bits，嵌在前6個低中頻系數上，則一幅載體圖像嵌入5400 bits，編碼冗余度為4.625；編碼水印W1的嵌入區域的起點為(17,17)，寬度和高度都是480，量化步長aj分別為JPEG量化表[23]對應系數的2.5倍。

圖5 原始測試圖像

水印的透明性可用原始圖像與嵌入水印的載體圖像之間的峰值信噪比PSNR[5]來表示。W2為48 bits，分別嵌入到圖像空域的3個特定位置，這3個特定位置應盡量選有一定紋理、邊緣等視覺不易感知的區域，奇偶量化步長Δ需考慮到視覺隱蔽性、魯棒性，根據所嵌區域紋理的不同，Δ取10～14之間的值，其中3.2節中的β取0.85，并且這3個特征位置的距離須盡量遠些，在本文中，W2的嵌入起點分別為(25,25)、(25,463)、(463,25)，每個大方塊嵌入16 bits，一個大方塊由16個小方塊組成，每個小方塊含36個像素。嵌入兩層水印后，它們對應的PSNR分別為41.2963 dB、41.4121 dB、41.1659 dB。

水印的魯棒性用原始水印與提取水印之間的相關系數NC[7]及提取水印的誤碼率BER[5]兩個參數來描述。

4.2 抗常見幾何攻擊

常見的幾何攻擊主要包括旋轉、縮放、剪切、錯切、仿射變換等。表1列出了本文算法抗此類攻擊的性能，并與文獻[6]的算法進行了對比。

表1 常見幾何攻擊下的BER

對于剪切攻擊，本文算法性能優異，表2為剪切攻擊下本文算法的NC。剪切攻擊后的圖像如圖6所示(以Lena為例)，被剪切部分補全黑。

在表1中，旋轉攻擊是不帶剪切的，仿射變換(1.007；1.010；1.013)對應的仿射矩陣分別是[1.007 0.01；0.01 1.012]；[1.010 0.013；0.009 1.011]；[1.013 0.008；0.011 1.008]；從表1可知，對于常見的幾何攻擊，本文算法與文獻[6]的BER相近，但本文的嵌入容量是其3倍，故而本文保持BER較低的情況下，嵌入容量有較大的提升。

表2 不同尺度剪切攻擊下的NC

圖6 不同尺度剪切攻擊后的圖像(Lena)

至于剪切攻擊，本文算法在較低剪切尺寸下，能夠完整的恢復水印，與文獻[8]的空間域(SW)、DCT域(DCTW)的實驗結果對比見表2。文獻[8]的嵌入容量是128 bits，魯棒性的評價指標是提取水印與原始水印之間的NC，表2中列出的是本文算法在剪切攻擊下NC的變化情況。只有在剪切尺度超過50%，LT碼的冗余度過小導致解碼不成功才會使NC急劇下降。

4.3 抗組合幾何攻擊

圖像在傳播過程中會遭受到多種多樣的攻擊，組合幾何攻擊就是比較常見的一種，表3列出了本文算法在部分組合幾何攻擊下BER的變化情況。

綜合以上的實驗結果可以推知，對于常見的幾何攻擊，即便是組合幾何攻擊，本文算法具有較好的性能，而且有較大的嵌入容量。因為本文算法對幾何攻擊的仿射矩陣進行了比較精確的估計。本文算法對于隨機刪除行列、隨機扭曲等攻擊稍差，因為本文算法是基于圖像的全局幾何校正。

表3 組合幾何攻擊下的BER

5 結束語

如何有效抵抗不同種類的幾何攻擊，同時保持較高的嵌入容量，一直是困擾水印研究者的一個難題。本文使用對仿射矩陣進行精確估計，并且在空間域嵌入一層水印對變換塊的邊界進行準確的定位的方法來解決此問題。首先利用SIFT算法提取攻擊前后圖像特征點，采用RANSAC算法對匹配的特征點對進行挑選，使用最小二乘法擬合出仿射矩陣，使仿射矩陣的估計誤差最小化，然后對受攻擊的圖像進行仿射逆變換以校正圖像的幾何形變，最后利用空間域水印精準定位出變換域版權水印的嵌入起點。實驗結果表明：本文算法不僅對于常見的幾何攻擊有較強的魯棒性，同時，相較于一般的水印算法，本文算法抗組合幾何攻擊性能較好且嵌入容量較大；更進一步，針對大部分魯棒水印算法抗剪切性能差的缺點，將水印信息經過LT碼編碼后嵌入到載體圖像中，充分發揮LT碼抗刪除的優點，因此本文算法還具有良好的抗剪切性能。

[1]Xin Y,Liao S,Pawlak M.Circularly orthogonal moments for geometrically robust image watermarking[J].Pattern Recognition,2007,40(12):3740-3752.

[2]Ryu SJ,Kirchner MJ,Lee MJ,et al.Rotation invariant localization of duplicated image regions based on Zernike moments[J].IEEE Transactions on Information Forensics & Security,2013,8(8):1355-1370.

[3]Wang Chunpeng,Wang Xingyuan,Xia Zhiqiu.Geometrically invariant image watermarking based on fast radial harmonic Fourier moments[J].Signal Processing:Image Communication,2016,45(C):10-23.

[4]Simitopoulos D,Koutsonanos DE,Strintzis MG.Robust image watermarking based on generalized radon transformations[J].IEEE Transactions on Circuits & Systems for Video Technology,2003,13(8):732-745.

[5]Li LD,Li SS,Abraham A,et al.Geometrically invariant image watermarking using polar harmonic transforms[J].Information Sciences,2012,199(16):1-19.

[6]He Xuansen,Zhu Tao,Yang Gaobo.A geometrical attack resistant image watermarking algorithm based on histogram modification[J].Multidimensional Systems & Signal Processing,2015,26(1):291-306.

[7]LI Leida,GUO Baolong,BIAO Jinfeng.Spatial domain image watermarking scheme robust to geometric attacks based on Odd-Even quantization[J].Journal of Electronics & Information Technology,2009,31(1):134-138(in Chinese).[李雷達,郭寶龍,表金峰.基于奇偶量化的空域抗幾何攻擊圖像水印算法[J].電子與信息學報,2009,31(1):134-138.]

[8]Lin YT,Huang CY,Lee GC.Rotation,scaling,and translation resilient watermarking for images[J].Image Processing Iet,2011,5(4):328-340.

[9]FANG Xiaozhao,ZHANG Wei,TENG Shaohua,et al.Di-gital watermarking scheme based on SVM of SIFT features[J].Computer Engineering & Design,2011,32(11):3609-3612(in Chinese).[房小兆,張巍,滕少華,等.基于SIFT特征區域的支持向量機數字水印方法[J].計算機工程與設計,2011,32(11):3609-3612.]

[10]Su PC,Chang YC,Wu CY.Geometrically resilient digital image watermarking by using interest point extraction and extended pilot signals[J].IEEE Transactions on Information Forensics & Security,2013,8(12):1897-1908.

[11]Zhang Li,Qian Gongbin,Xiao Weiwei.Geometric distortions invariant blind second generation watermarking technique based on Tchebichef moment of original image[J].Journal of Software,2007,18(18):2283-2294.

[12]LOU Oujun,WANG Zhengxuan.A Contourlet-domain watermarking algorithm against geometric attacks based on feature template[J].Chinese Journal of Computers,2009,32(2):308-317(in Chinese).[樓偶俊,王鉦旋.基于特征點模板的Contourlet域抗幾何攻擊水印算法研究[J].計算機學報,2009,32(2):308-317.]

[13]WANG Chuntao,NI Jiangqun,ZHUO Huashuo,et al.A geometrically invariant robust image watermarking based on deformable multi-scale transform[J].Acta Automatica Sinica,2011,37(11):1368-1380(in Chinese).[王春桃,倪江群,卓華碩,等.基于可變形多尺度變換的幾何不變魯棒圖像水印算法[J].自動化學報,2011,37(11):1368-1380.]

[14]Wang Xiangyang,Liu Yunnan,Li Shuo,et al.Robust image watermarking approach using polar harmonic transforms based geometric correction[J].Neurocomputing,2016,174(22):627-642.

[15]Lowe DG.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(60):91-110.

[16]Mackay DJC.Fountain codes[J].IEE Proceedings Communications,2005,152(6):1062-1068.

[17]Korus P,Biaas J,Dziech A.A new approach to high-capacity annotation watermarking based on digital fountain codes[J].Multimedia Tools & Applications,2014,68(1):59-77.

[18]Mikolajczyk K,Schmid C.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.

[19]Bay H,Ess A,Tuytelaars T,et al.Speeded-up robust features[J].Computer Vision & Image Understanding,2008,110(3):346-359.

[20]Luo J,Gwun O.A comparison of SIFT,PCA-SIFT and SURF[J].International Journal of Image Processing,2009,3(4):143-152.

[21]ZHAO Xiaochuan.Improve and applicable case detail of processing technology of modern digital image(MATLAB Version)[M].Beijing:Beihang University Press,2012:44-74(in Chinese).[趙小川.現代數字圖像處理技術提高及應用案例詳解(MATLAB版)[M].北京:北京航空航天大學出版社,2012:44-74.]

[22]DENG Cheng,GAO Xinbo.Geometrically robust image watermarking based on SIFT feature regions[J].Guangzi Xuebao,2009,38(4):1005-1010(in Chinese).[鄧成,高新波.基于SIFT特征區域的抗幾何攻擊圖像水印算法[J].光子學報,2009,38(4):1005-1010.]

[23]SU Na.Research and application of digital wartermarking algorithm based on DCT transform domain[D].Chengdu:University of Electronic Science and Technology of China,2016(in Chinese).[蘇娜.基于DCT域的數字圖像水印算法的研究與應用[D].成都:電子科技大學,2016.]