混沌元胞果蠅算法在云計算中的應用
戰 非,曹國震,王建軍,張少茹
(1.西安航空學院 計算機學院,陜西 西安 710077;2.西安交通大學 醫學院護理系,陜西 西安 710049)
0 引 言
果蠅算法(fruit fly optimization,FOA)[1,2]應用在云計算中對海量數據進行處理,解決大型復雜問題時存在一定的缺點,包括初值的選擇對算法求解精度存在影響、收斂速度慢、易陷入局部最優等[3]。近年來研究者們針對標準果蠅算法提出了相關的改進策略。如文獻[4]中提出通過引入果蠅因子,自適應調整果蠅搜索步長,提高算法速度;文獻[5]中引入免疫記憶特性,對果蠅算法的解進行優化,避免出現早熟現象;文獻[6]中提出遞減步長的果蠅算法進行優化;文獻[7]中通過將迭代尋優過程分為果蠅移動范圍逐步增大和逐步減小兩個階段,以提高種群多樣性等。
上述研究者對果蠅算法的改進主要集中在優化迭代過程的中間解,沒有過多考慮初始解群的優劣對算法的影響。本文提出一種引入混沌理論和結合元胞自動機的改進算法,通過結合混沌運動的優勢,將優化變量通過Logistic映射規則映射至混沌變量空間內,利用混沌變量特點尋優搜索,再將得到的優化解線性轉至優化空間,完成初始解群的優化。然后在算法迭代過程中,利用元胞自動機演化規律,進行最優種群的選擇和替換。最后在云計算環境下通過實驗驗證了該算法在求解精度和收斂速度上更優。
1 果蠅算法
1.1 算法原理
果蠅算法基于自然界果蠅種群的覓食行為,果蠅個體通過嗅覺區分空氣中的不同味道,同時通過視覺發現食物和身邊果蠅同伴的位置,通過判斷調整飛行的方向[8]。算法具體流程如下:
(1)初始化種群規模sizePop和算法最大迭代次數maxGen,隨機生成果蠅群體初始位置X_axis和Y_axis;
(2)計算果蠅個體嗅覺尋找食物的隨機方向和距離
(1)
其中,Xi和Yi表示下一位置的橫坐標和縱坐標,Value代表搜索距離,rand()代表0到1的隨機數;
(3)因無法確定食物位置,需估算果蠅個體與原點距離矢量Di,然后計算味道濃度判定矢量Si
(2)
(3)
(4)將Si代入味道濃度判定函數,即適應度函數,計算得出每個果蠅個體位置的適應度(即味道濃度)Smelli
Smelli=fit(Si)
(4)
(5)尋找出當前果蠅種群中最佳適應度Smellg和最佳位置坐標xg、yg;
(6)令Smellbest=Smellg,將當前種群最佳位置作為新一次算法迭代的初始位置,即X_axis=xg,Y_axis=yg,此時果蠅種群利用視覺飛向該位置;
(7)重復執行步驟(2)~步驟(5),判斷最佳適應度是否優于上次迭代產生的最佳適應度,同時當前迭代次數是否小于最大迭代次數,若是則執行步驟(6)。
1.2 蠅算法的不足
判斷算法的優劣,可以從收斂性、求解精度和執行效率等方面評判。收斂性是指隨著算法的迭代執行,算法結果逐漸逼近真實結果進而趨近于一個穩定的值,趨近固定值的過程越快即收斂性越好。求解精度通俗來講指算法進行最優值求解時,最優解的小數點后的位數,位數越高代表算法求解精度越高,算法也越優。執行效率指算法執行的時間,一般而言時間越短效率越高,算法也越優。
由于云計算中數據量巨大,處理問題較為復雜,同時云服務應用于互聯網的特點又要求具有相對較高的執行效率和響應速度。基本果蠅算法應用在云計算中存在以下缺點:
(1)算法求解精度對初值的選擇呈現出敏感性和不穩定性,初值選擇較好能夠獲得較高的求解精度,初值選擇不當可能引起求解精度降低。由于果蠅算法初值完全依賴隨機選擇,不具備有界性及遍歷性,導致算法易出現不穩定性。
(2)果蠅算法迭代過程中,每次僅選擇本次迭代得到的最優個體,所有果蠅飛向當前最優位置,但若當前最優非全局最優,則易出現收斂速度慢、易發散和陷入局部最優等現象,影響云計算效率。
2 元胞自動機
元胞自動機(cellularautomata,CA),代表一種時間和空間離散的動力系統,散布在規則網格中的個體元胞取有限的離散狀態,遵循同樣的作用規則,依據確定的局部規則進行更新同步。元胞個體周圍根據相應規則劃定的元胞集合稱為鄰居,當前元胞的下一時刻狀態根據自身及其鄰居狀態確定[9]。


圖1 元胞自動機鄰居模型
元胞演化規則為:
(1)根據圖1中擴展Moore鄰居模型規定,選擇陰影區域Mi(i=1,2,…)的中心元胞,計算所有區域的最佳味道濃度(即適應度)作為初始值,Vibest=min(f(si0),f(si0),…,f(si0)),其中si0為味道濃度判斷值。
(2)對單個區域Mi,取其中的任意元胞Ci,計算Vi=f(s1),f(s2),…,f(si),若Vi 本文主要利用元胞自動機的演化規則,對果蠅算法每一輪迭代的解進行優化處理。 混沌是一種按照特定規律運動的非線性現象,在一定范圍內可以實現無重復遍歷。本文討論的混沌主要指一種對初始條件較敏感的時間演化行為,具有有界性和遍歷性的特征。有界性指通過混沌吸引子,混沌運動的軌跡始終規定于一個確定區域。遍歷性是指在混沌運動的范圍內能夠遍歷所有狀態[10,11]。本文的研究和實驗都基于Logistic映射,其迭代公式為 xi+1=μxi(1-xi),i=0,1,2…,0<μ≤4 (5) 其中,μ為控制參數,xi+1∈(0,1)。當3.569 945 6<μ≤4時,Logistic映射表現出混沌狀態;當μ=4時,呈現典型混沌特征。 本文通過Logistic映射進行混沌優化策略如下: (1)產生隨機混沌量。 對式(5)取取μ=4,并進行變換產生混沌變量Cxi,公式如下 Cx(n+1)i=4Cx(n)i(1-Cx(n)i),i=0,1,… (6) 其中,Cx(n)i指所產生的混沌變量Cxi在第n步混沌變換后的值。 (2)優化變量和混沌變量進行往返映射[12]。 Cxi=(xi-ai)/(bi-ai) (7) (8) 以上步驟就完成了將優化變量映射至混沌空間,然后可以利用混沌系統的有界性和遍歷性進行優化,再將優化解轉換回優化空間。 根據前文分析果蠅算法在云計算中的缺點,這里提出一種結合混沌理論和元胞自動機演化規則的改進算法—混沌元胞果蠅算法(CCF)。算法具體改進策略如下: (1)針對果蠅算法對初值的敏感性和不穩定性,引入混沌映射對初值進行優化。由于果蠅算法隨機選擇的初值不具備遍歷性和有界性,對求解精度有較大的影響,這里利用混沌映射的遍歷性和有界性,先將果蠅算法產生的初值即優化變量,通過Logistic映射到混沌空間,使其具有混沌特性,然后再轉換回優化變量空間,完成對初值的優化。 (2)針對果蠅算法易陷入局部最優和收斂速度慢的缺點,引入元胞自動機的演化規則進行最優種群選擇,根據演化所得適應度和當前最優適應度進行比較和替換,使果蠅種群跳出局部最優。 這里提出的混沌元胞自動機果蠅算法(CCF)的算法流程如下: (2)根據式(7)將Zi各分量映射為混沌變量Cz(n)i,Cz(n)i∈[0,1]; (3)根據式(6)對Cz(n)i的各分量進行混沌操作; (5)將果蠅個體適應度值放入F[m][n]二維數組中,依次按行放置,根據擴展Moore鄰居模型取n=5,m=sizePop/5; (6)根據本文第2節中元胞自動機演化規則,選擇果蠅優秀個體并保留最優個體位置,復制并替換之前的果蠅位置; (7)執行第1節中果蠅算法的步驟(2)~步驟(6),記錄果蠅種群中最佳適應度Smellbest和最佳位置坐標xg、yg; (8)判斷最佳適應度是否優于上次迭代產生的最佳適應度,同時當前迭代次數是否小于最大迭代次數,若是轉至步驟(5)。 本次實驗采首先采用Sphere函數、Ackley函數、Schwefel1.2函數和Zakharov函數對CCF算法的求解精度和收斂性進行測試,實驗結果橫向比較標準果蠅算法(FOA)。為了體現兩種算法測試過程中的公平性,測試過程沒有放入分布式計算環境中進行。該4種高維優化測試函數解得分布都比較復雜,函數存在較多的拐點和障礙,在進行最小值求解時易陷入局部最優。4種函數公式分別為: (1)Sphere函數如式(9)所示 (5)在數組O=[ot,r]4×r的第四行中,隨機改變某子批量在工序間流轉過程中的搬運設備,并按照FCFS規則生成搬運設備選擇相鄰解。 (9) (2)Ackley函數如式(10)所示 (10) (3)Schwefel1.2函數如式(11)所示 (11) (4)Zakharov函數如式(12)所示 (12) 4種函數的特征見表1。 表1 4種測試函數的特征 實驗中設最大迭代次數maxGen=250,種群個數sizePop=50,算法單獨執行30次,測試函數維數分別取10維、30維和50維。對比標準果蠅算法(FOA)結果見表2。 由表2中的數據分析可得,CCF算法通過引入混沌映射對算法初值進行優化,所得到解的精度要遠高于FOA算法,平均值也比FOA算法更逼近測試函數的最優解。以Zakharov函數為例,FOA算法在求解精度較低時已經陷入局部最優且無法跳出,但是CCF算法卻能夠在更大范圍內搜索,并獲得較好的最優解。綜合數據表明CCF算法能夠較有效地跳出局部最優,優于FOA算法。 表2 測試函數實驗結果 設4種測試函數維數為30,取CCF算法一次執行過程中迭代收斂曲線如圖2~圖5所示。 圖2 Sphere函數迭代曲線 由圖2~圖5可以分析得出,CCF算法在經過混沌初值變換和每輪迭代過程中進行元胞自動機演化,有效提高了算法的收斂速度,執行效率要高于FOA算法。 通過CloudSim云仿真軟件搭建實驗環境,創建云計算節點和分發任務數,設定服務參數和創建虛擬機。模擬資源調度對CCF算法進行測試,根據服務要求搜索最優路徑。仿真中使用特定函數的參數如帶寬(bw),內存(ram),PE數(pesNumber)等的設置,根據目前常規虛擬機硬件水平設置[13-15],仿真流程如圖6所示。 圖3 Ackley函數迭代曲線 第一部分實驗:取計算節點為20,任務數由20變化至100,CCF算法和FOA算法各執行20次,結果取平均值,同時計算任務分配結果的相對標準差。實驗結果如圖7和圖8所示。 第二部分實驗:由于受虛擬機條件制約,實驗模擬的云環境從規模上要遠小于實際中的云計算環境,為了表現云規模即計算節點數量對算法的影響,固定任務數為40,計算節點數為10變化至80,執行過程不變,在每個變化節點數上CCF和FOA算法各執行10次取平均值,執行時間如圖9所示。 圖4 Schwefel 1.2函數迭代曲線 圖5 Zakharov函數迭代曲線 圖6 CloudSim仿真流程 圖7 任務執行時間對比 圖8 相對標準差結果 圖9 不同節點對應執行時間對比 由圖7和圖8分析可得,隨著任務數的增加,CCF算法的執行時間要優于FOA算法,當任務數越多,CCF算法效率優勢越明顯,符合云計算的需要。同時CCF算法的偏差值隨著任務數的增加也越來越小趨于線性漸進,也優于FOA算法。由圖9分析可得,當計算節點數量增多,CCF改進算法在執行效率上越來越優于經典的果蠅算法。綜上所得,本文提出的混沌元胞果蠅算法能夠較好的克服果蠅算法的不足,更加適用于云計算。 本文在標準果蠅算法的基礎上引入混沌理論和元胞自動機演化規則對其進行改進,提出了混沌元胞果蠅算法(CCF)。該算法利用混沌運動的特征對算法初值進行優化,然后在每一輪算法迭代中通過元胞自動機演化規則去優化果蠅種群,尋找最優適應度并進行替換。通過優化測試函數實驗和云仿真實驗,驗證混沌元胞果蠅算法在求解精度、收斂性和執行效率上要優于果蠅算法,更適合應用在云計算中。本文算法只是用混沌映射進行初值的優化,若每輪迭代都引入混沌特征進行優化結果如何,還需要后期進一步的研究。 [1]PAN Wenchao.Fruit fly optimization[M].Taipei sea Book Company,2011:1-12(in Chinese).[潘文超.果蠅最佳化演算法[M].臺北滄海書局,2011:1-12.] [2]XIAO Zheng’an.Design of analog filter based on fruit fly optimization algorithm[J].Journal of Hubei University of Education,2012,29(2):26-29(in Chinese).[肖正安.基于果蠅優化算法的模擬濾波器設計[J].湖北第二師范學院學報,2012,29(2):26-29.] [3]LIU Zhengwei,WEN Zhongling,ZHANG Haitao.Cloud computing and cloud data management technology[J].Journal of Computer Research and Development,2012,49(S1):26-31(in Chinese).[劉正偉,文中領,張海濤.云計算和云數據管理技術[J].計算機研究與發展,2012,49(S1):26-31.] [4]YANG Shuquan,SHU Qin,HE Chuan.A modified fruit fly algorithm and its application in PPI network[J].Computer Applications and Software,2014,31(12):292-294(in Chinese).[楊書佺,舒勤,何川.改進的果蠅算法及其在PPI網絡中的應用[J].計算機應用與軟件,2014,31(12):292-294.] [5]WANG Xin,DU Kang,QIN Bin,et al.Drying rate modeling on FOALSSVR[J].Control Engineering of China,2012,19(4):631-638(in Chinese).[王欣,杜康,秦斌,等.基于果蠅優化算法的LSSVR干燥速率建模[J].控制工程,2012,19(4):631-638.] [6]NING Jianping,WANG Bing,LI Hongru,et al.Research on and application of diminishing step fruit fly optimization algorithm[J].Journal of Shenzhen University Science and Engineering,2014,31(4):368-372(in Chinese).[寧劍平,王冰,李洪儒,等.遞減步長果蠅優化算法及應用[J].深圳大學學報理工版,2014,31(4):368-372.] [7]XU Fuqiang,TAO Youtian,LYU Hongsheng.Improved fruit fly optimization algorithm[J].Journal of Soochow University(Natural Science Edition),2014,29(1):17-20(in Chinese).[徐富強,陶有田,呂洪升.一種改進的果蠅優化算法[J].蘇州大學學報,2014,29(1):17-20.] [8]HAN Junying,LIU Chengzhong.Fruit fly optimization algorithm with adaptive mutation[J].Application Research of Computers,2013,30(9):2641-2644(in Chinese).[韓俊英,劉成忠.自適應變異的果蠅優化算法[J].計算機應用研究,2013,30(9):2641-2644.] [9]YAO Canzhong,YANG Jianmei.Cellular automata simulation of group behavior driven by dual-targets[J].Computer Engineering and Applications,2012,48(1):27-29(in Chinese).[姚燦中,楊建梅.雙目標推動下群體行為的元胞自動機模擬[J].計算機工程與應用,2012,48(1):27-29.] [10]ZHAN Fei,ZHANG Shaoru.A research on application optimization of cloud computing based on chaos ant colony algorithm[J].Fire Control & Command Control,2017,42(7):25-28(in Chinese).[戰非,張少茹.基于混沌蟻群算法的云計算應用優化研究[J].火力與指揮控制,2017,42(7):25-28.] [11]LI Wen,LIANG Ximing.A hybrid algorithm based on chaos optimization and steepest descent algorithm[J].Computing Technology and Automation,2003,22(2):12-14(in Chinese).[李文,梁昔明.基于混沌優化和最速下降法的一種混合算法[J].計算機技術與自動化,2003,22(2):12-14.] [12]MO Yuanbin,CHEN Dezhao,HU Shangxu.Chaos particle swarm optimization algorithm and its application in biochemical process dynamic optimization[J].Journal of Chemical Industry and Engineering(China),2006,57(9):2123-2127(in Chinese).[莫愿斌,陳德釗,胡上序.混沌粒子群算法及其在生化過程動態優化中的應用[J].化工學報,2006,57(9):2123-2127.] [13]ZHAN Fei,ZHANG Shaoru.Chaos harmony search algorithm base on scheduling of cloud computing[J].Computer Engineering and Design,2017,38(7):1823-1827(in Chinese).[戰非,張少茹.基于混沌和聲的云計算調度算法[J].計算機工程與設計,2017,38(7):1823-1827.] [14]ZHAN Fei,ZHANG Shaoru.A research on cloud computing scheduling based on chaos particle swarm optimization algorithm[J].Electronic Design Engineering,2017,25(5):13-17(in Chinese).[戰非,張少茹.基于混沌粒子群算法的云計算調度研究[J].電子設計工程,2017,25(5):13-17.] [15]ZHAN Fei,ZHANG Shaoru.Research on applications of chaos cuckoo search algorithm suitable for cloud computing[J].Control Engineering of China,2017,24(7):1486-1492(in Chinese).[戰非,張少茹.適應云計算的混沌布谷鳥算法應用優化研究[J].控制工程,2017,24(7):1486-1492.] [16]QIAN Fucai,FEI Chuhong,WANG Baiwu.A hybrid algorithm for finding global minimum[J].Information and Control,1998,27(3):232-235(in Chinese).[錢富才,費楚紅,萬百五.利用混沌搜索全局最優的一種混合算法[J].信息與控制,1998,27(3):232-235.] [17]Li J,Jia C,Li J,et al.Outsourcing encryption of attribute-based encryption with MapReduce[C]//Information and Communications Security-14th International Conference.Berlin:Springer Berlin Heidelberg,2012:191-201. [18]Hao M,Wlodarczyk TW,Rong C.Performance analysis and optimization of map only left outer join[C]//Proceedings of the 27th International Conference on Advanced Information Networking and Applications Workshops IEEE Computer So-ciety.New York:ACM,2013:625-631.3 Logistic混沌映射轉換


4 混沌元胞果蠅算法研究
4.1 算法改進策略
4.2 算法流程
5 實驗及分析
5.1 優化函數測試



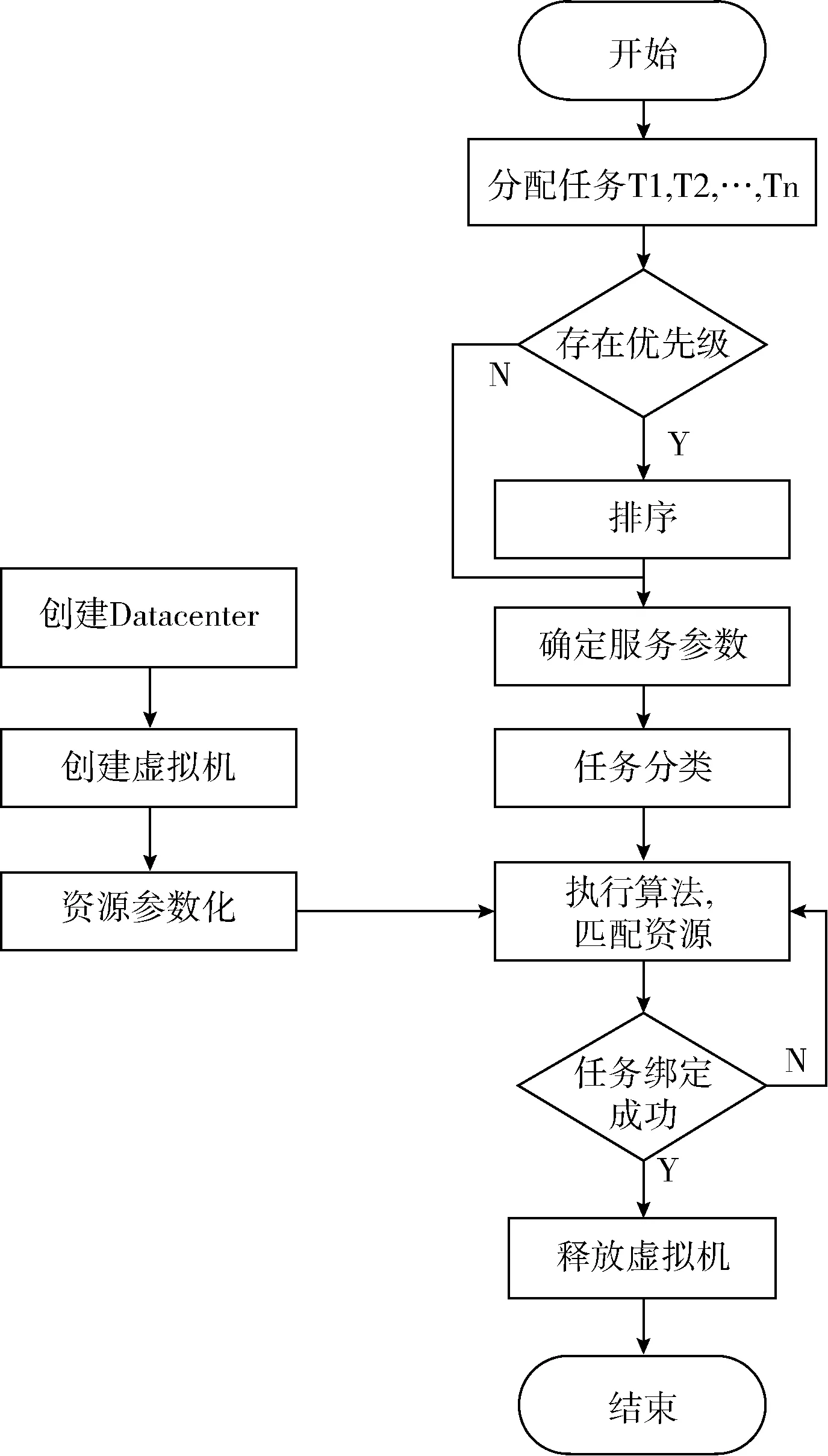
5.2 云仿真實驗






6 結束語

