基于鄰域旋轉體積的關鍵點描述子及其應用

霍 旺，熊風光，韓 燮，況立群

(中北大學 計算機與控制工程學院，山西 太原 030051)

0 引 言

點云關鍵點的特征描述作為點云配準與識別等處理中的關鍵步驟，有著重要的意義與廣闊的應用前景。與網格模型相比，散亂的點云數據之間缺少相應的拓撲關系，對關鍵點的描述更加困難。現有的一些描述算法在運行效率、配準的準確率及抗噪、抗干擾的能力上仍有不足，需要進一步的改進提高。

1 相關工作

針對最近點迭代(iterative closet point，ICP)算法存在的收斂速度慢、計算復雜度高的問題，許多學者提出了先將點云的關鍵點配準，使兩片點云具有良好的初始位置，再利用ICP或其改進算法[1,2]對點云進行精配準的方法。同時提出了許多優秀的關鍵點描述子算法。但在運行效率、算法的魯棒性上，仍未取得令人滿意的效果，需要人們繼續改進和創新。一個有效的關鍵點描述子必須滿足以下條件[3]：①描述子應具有較強的鑒別力；②描述子應具有豐富的描述性和穩健的變換不變性；③描述子應易于計算和匹配；④描述子應對噪聲和背景干擾具有較強的穩健性。

目前的描述子根據其描述方式大致可以分為二類：

(1)基于點云空間數據點位置分布的方法。Johnson于1999年提出Spin Image(SI)特征是該類的經典代表。該方法以關鍵點為圓心，其法向量為z軸構建圓柱參考系，將鄰域點的分布密度作為描述的特征。Spin Image對遮擋和干擾具有很強的穩定性，但對點云數據有一定要求，需要點云均勻分布并且需要較大的存儲空間。隨后Frome提出的3D Shape Context(3DSC)改變了Spin Image投影到二維平面的方式，將鄰域劃分為三維的球形柵格，統計點云在球形柵格中的特征，其抗噪和抗干擾的性能相比SI均有提高，但進行描述子匹配時需要將場景進行旋轉，計算量較大。Rotational Projection Statistics(RoPS)[4-6]是Yulan Guo提出的一種關鍵點描述子。該方法針對網格表面，在關鍵點周圍建立局部坐標系，將鄰域點投影到XOY、YOZ和XOZ這3個2D平面上，并在三平面上建立橫平豎直的單元格，根據落到每個單元格的點的數量，來計算每個2D平面上的一系列統計數據(低階中心矩和熵值)從而進行描述，并且旋轉模型增加不同視點時的魯棒性。RoPS描述子對關鍵點的描述能力和穩定性都具有了明顯的提高，但該方法是基于網格模型進行地描述，而非針對大多數設備獲取到的三維點云模型，因此需先對三維點云模型進行三角網格化，而且還要執行多次旋轉操作，描述過程較為復雜和耗時。

(2)基于關鍵點及其鄰域點之間幾何關系的方法。這類方法比較有代表性的是Rusu R.B提出的Point Feature Histogram(PFH)特征和改進算法Fast Point Feature Histogram(FPFH)等相關算法[7,8]。該方法是將關鍵點鄰域內每一對點建立達布坐標系(Darboux frame)，計算法向量與坐標系的夾角，形成能描述關鍵點鄰域關系的直方圖。FPFH算法的優點是算法簡單、計算速度快，缺點是抗噪性差。Signature of Histogram of Orientations(SHOT)[9]特征描述了鄰域內不同空間位置點的法向量與局部坐標系的夾角關系。其具有很好的抗噪性，但描述子的維數達到了352維之巨，因此計算時間較長。

本文提出一種建立在局部坐標系的基礎上，首先對關鍵點的鄰域點進行區間劃分，然后對各個區間內鄰域點與投影到特定平面上的投影點所形成的各個梯形進行360°旋轉，最后通過計算經旋轉后得到的空間模型的體積的數值對該區間進行描述，形成一個對關鍵點的多區間體積值進行表述的描述子。本文提出的描述子描述的也是關鍵點及其鄰域點之間幾何關系。描述子利用了局部坐標系，因此具有良好的旋轉平移不變性；同時，關鍵點及其鄰域點投影形成的幾何模型的體積計算方法簡單易行、效率高，并且最終所形成的描述子的低維度性有利用后期描述子的匹配。

2 描述子建立過程

(1)獲取關鍵點p的鄰域點。以關鍵點p為球心，R為半徑建立一個p的鄰域球，記為S，包含在該球內的所有點即為p的鄰域點，記為Nbhd(p)。本文采用KD-Tree進行空間鄰域點搜索，加速關鍵點的鄰域點的查找速度。

(1)

(2)

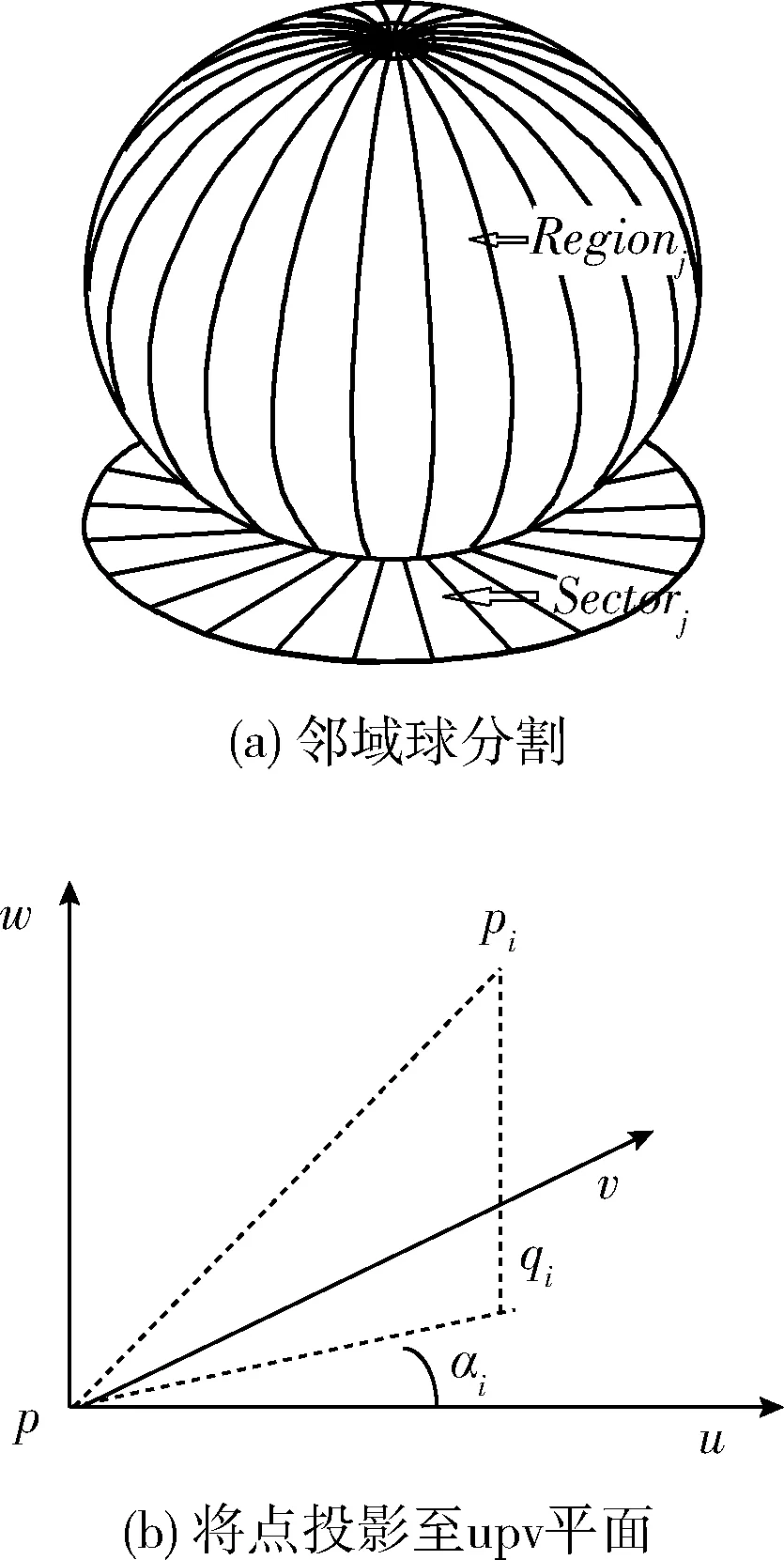
圖1 空間的幾何區間

圖2 任一空間區域側視圖

在計算Regionk中兩相鄰鄰域點及其投影點所形成的梯形旋轉后的模型的體積Vk,i時，可將該模型拆分為一個空心圓柱體Modelk,i,1和一個中間為空心圓柱的圓臺Modelk,i,2。Modelk,i,1的體積Vk,i,1可用式(4)進行計算，其中，hk,i,1代表的Modelk,i,1的高，rk,i-1和rk,i分別代表Modelk,i,1的內、外半徑，均可通過式(6)進行計算。Modelk,i,2的體積Vk,i,2可由圓臺的體積Vk,i,3與圓柱的體積Vk,i,4相減而得，見式(7)。式(8)用于計算體積Vk,i,3,其中hk,i,2代表圓臺的高，rk,i-1和rk,i分別代表圓臺的內、外半徑，也通過式(6)進行計算。式(9)用于計算體積Vk,i,4，其中hk,i,2代表空心圓柱的高，通過式(10)進行計算，rk,i-1代表圓柱的半徑。另外，rk,0=0，hk,0,1=R

(3)

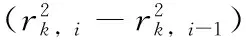
(4)

(5)

(6)

Vk,i,2=Vk,i,3-Vk,i,4

(7)

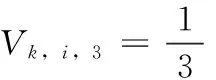
(8)

(9)

hk,i,2=hk,i-1,1-hk,i,1

(10)

(6)依據步驟(5)，計算關鍵點p的其它m-1個維度的數值，最終組成一個m維的描述子。

3 實驗結果及分析

實驗采用與PFH、FPFH、SHOT描述子在運行時間、旋轉平移魯棒性、抗噪性和降采樣方面進行對比分析。三維模型使用斯坦福大學的標準三維模型庫中的Bunny、Armadillo和Happy Buddha，以增加不同模型情況下的對比性。本文所提出的描述子代碼采用VS2013平臺+PCL庫實現，且PFH、FPFH、SHOT在PCL中有開源代碼，可以很方便地進行對比分析；另外，本實驗中設定m為24，點云的法向量是基于最近的10個鄰近點獲取的，鄰域半徑R為18倍的點云分辨率。

3.1 運行時間分析

表1是實驗用的模型信息，記錄了各模型中點的個數和獲取到的關鍵點的個數，本文利用PCL中提供的HarrisKeypoint3D類將提取到Harris 3D角點作為關鍵點。表2記錄了4種描述子的維數和在不同模型下生成關鍵點的描述子所需運行時間的對比。從表2可以看出本文提出的描述子無論是維數、計算時間都較小，意味著所需的存儲空間較小、計算效率更高、實時性將更好，其原因是本文所提出的描述子只需要計算關鍵點處的局部坐標系和各鄰域內的體積和，不需要計算其它額外的參數(如：法向量、網格等)，所以運行時間大大縮短。最終的運行時間只與關鍵點的多少有關，而和模型的點數等其它參數無關。

表1 實驗模型信息

表2 各個方法不同模型的運行時間

注意本文實驗出現了PFH比FPFH快的情況。其原因是實驗采用的是對關鍵點而不是整個點云進行的描述。根據FPFH的原理相當于擴大了鄰域搜索半徑，但由于計算的關鍵點數目較少，FPFH提高的效率不能彌補擴大半徑的帶來的劣勢。故而會出現下表中PFH比FPFH快的情況，但這并不影響對結果的分析。

3.2 旋轉平移的魯棒性分析

在三維點云獲取過程中經常由于物體形狀、設備等限制，不能獲取連續的、視點不變的點云，經常帶有一定的旋轉角度。因此，描述子旋轉平移的魯棒性是評價一個描述子的重要標準。

匹配準確率=正確匹配的描述子對的數目/匹配的描述子對的數目

(11)

圖3為3個模型在不同描述子下的旋轉平移不變的魯棒性分析結果。從圖3中可以看出本文提出的描述子與其它描述子相比，對旋轉平移具有更好的穩定性。在旋轉較大角度時仍有較高的準確率，同時針對不同模型表面都能有較好的表現。分析原因主要有：一是本文采用基于關鍵點建立局部坐標系的方式進行描述，本身局部坐標系具有良好的旋轉平移魯棒性；二是采用模型幾何體積分布的方式對局部點云進行描述，只要是模型的幾何結構不發生變化，經旋轉平移后仍能保持局部點云的體積分布不變。

3.3 抗噪性分析

在三維點云數據的獲取過程中，由于人為、環境的干擾或者掃描設備本身的設計缺陷、精度限制等問題，使得獲取到的點云數據多帶有一定的噪聲。因此，需要對點云加入高斯噪聲，并進行旋轉平移魯棒性檢驗來考察描述子的抗噪性能。

圖3 旋轉平移的魯棒性分析

圖4 抗噪性分析

從圖4可以看出相較于其它描述子而言，本文所提出的描述子具有很好抗噪性，究其緣由，還是因為本文所提出的描述子僅僅是描述關鍵點的空間幾何體積，只要是噪聲沒有對模型的幾何結構產生重大的影響，描述子的穩定性就不會發生太多變化。

3.4 不同采樣率分析

生產、生活中，經常會有采樣設備的硬件、配置不同等情況，獲取的點云的采樣率也不盡相同。因此，基于不同采樣率，實驗測試描述子的性能顯得尤為重要。

本次實驗的過程為：給定一個模型M、一個真實的旋轉平移矩陣Rt，M進行采樣率為δ的降采樣后的模型記為Mδ，Mδ在Rt的映射下的模型為Mδ′；然后按照3.2中的實驗依據模型M、Mδ′和旋轉平移矩陣Rt進行旋轉平移魯棒性分析。實驗結果如圖5所示。

圖5 多采樣率分析

從圖5可以清晰看出本文所提出的描述子，在采樣率為3/4左右時，具有良好的效果，在采樣率為1/2左右時，性能接近于其它描述子，而當采樣率為1/4左右時，性能差于其它描述子，其原因是本文的描述子在分辨率下降較多的情況下，內部幾何結構發生較大改變，體積計算產生較大的誤差，影響了描述子的性能。

4 本文描述子的應用

將本文所提出描述子應用于點云配準中，實現多視角下點云的對齊操作。實驗數據為斯坦福大學提供的不同視角下的兔子的點云模型，包括從0°、45°、90°、180°、270°和315°的6個不同視角下掃描的點云。其中兩片點云的配準過程為：

(1)載入視角相鄰的兩片點云(如：0°、45°)記為source、target，并分別提取Harris 3D角點作為關鍵點集合keys_src和keys_tgt，利用本文提出的方法對關鍵點進行描述，獲得兩組描述子集合feature_src和feature_tgt，其中關鍵點集合中的關鍵點與描述子集合中的描述子是一一對應的；

(2)隨機選取feature_src中的3個描述子fs0、fs1和fs2，置入集合fs中，利用KD-Tree在feature_tgt中為fs0搜索5個最近的描述子，并隨機選取一個描述子ft0作為fs0對應描述子，依次計算出fs1的對應描述子ft1，fs2對應描述子ft2，將ft0、ft1和ft2置入集合ft中；

(3)找到fs0、fs1和fs2對應的關鍵點ks0、ks1和ks2，依次連接該3點形成3條邊并計算它們的歐式距離，分為記為d_ks01、d_ks12和d_ks20，同理計算ft0、ft1和ft2對應關鍵點所形成3條邊的歐式距離，分別記為d_kt01、d_kt12和d_kt20，依次計算對應邊距離的相似比，即min(d_ks01/d_kt01，d_kt01/d_ks01)、min(d_ks12/d_kt12，d_kt12/d_ks12)和min(d_ks20/d_kt20，d_kt20/d_ks20)，如果相似比均大于一定閾值(本文為0.8)時則繼續步驟(4)，否則退回到步驟(2)；

(4)利用步驟(3)找到的3對關鍵點、和，計算出旋轉矩陣平移Rt；

(6)循環n次(本文為50000)執行步驟(2)～步驟(5)，選取最小fitness時的旋轉平移矩陣作為最終的旋轉平移矩陣。根據這個旋轉平移矩陣可以將source變換到target同一坐標系下，完成根據關鍵點對點云的配準工作。

對每兩個相鄰的點云片依次執行上面的操作，最終可以將6片點云都變換到同一坐標系下，得到完整的模型。本文的配準結果如圖6所示。

圖6 基于本文所提出的描述子的配準

從圖6可以看出，配準結果還是相對較好的。基本上吻合了兔子本身的位置，雖然耳朵等處有些誤差，但仍在可接受的范圍內。達到了粗配準的要求，可以為后續精確配準提供良好的初始條件。

5 結束語

本文提出了一個基于關鍵點鄰域旋轉體積特征的描述方法。實驗結果表明，針對不同點云模型都具有非常好的旋轉平移魯棒性，同時具有描述過程中所需存儲空間較小，運行速度快的優勢。在模型具有噪聲、采樣率差別較小的情況下仍有良好的表現。比PFH、FPFH和SHOT等描述子運行的更快，更穩定，且應用在多片點云的粗配準上也達到了較好的效果，為下一步的精配準做了良好的鋪墊。但是在模型采樣率差別較大的情況下，效果并不理想，接下來的研究可以針對此問題進行改進。

[1]Chen J,Belaton B.An improved iterative closest point algorithm for rigid point registration[J].Communications in Computer & Information Science,2014,481:255-263.

[2]Tagliasacchi A,Schr?der M,Tkach A,et al.Robust articulated-ICP for real-time hand tracking[J].Computer Graphics Forum,2015,34(5):101-114.

[3]GUO Yulan,LU Min,TAN Zhiguo,et al.Survey of local feature extraction on range images[J].Pattern Recognition and Artificial Intelligence,2012,25(5):783-791(in Chinese).[郭裕蘭,魯敏,譚志國,等.距離圖像局部特征提取方法綜述[J].模式識別與人工智能,2012,25(5):783-791.]

[4]Guo Y,Sohel F,Bennamoun M,et al.Rotational projection statistics for 3d local surface description and object recognition[J].International Journal of Computer Vision,2013,105(1):63-86.

[5]Guo Y,Bennamoun M,Sohel FA,et al.3D free form object recognition using rotational projection statistics[C]//Applications of Computer Vision.FL:IEEE,2013:1-8.

[6]Guo Y,Sohel F A,Bennamoun M,et al.RoPS:A local feature descriptor for 3D rigid objects based on rotational projection statistics[C]//International Conference on Communications,Signal Processing, and Their Applications.Sharjah:IEEE,2013:1-6.

[7]Rusu RB,Bradski G,Thibaux R,et al.Fast 3D recognition and pose using the Viewpoint Feature Histogram[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Taipei:IEEE,2014:2155-2162.

[8]Li P,Wang J,Zhao Y,et al.Improved algorithm for point cloud registration based on fast point feature histograms[J].Journal of Applied Remote Sensing,2016,10(4):045024.

[9]Salti S,Tombari F,Di stefano L.Shot:Unique signatures of histograms for surface and texture description[J].Computer Vision and Image Understanding,2014,125(8):251-264.

[10]Zaharescu A,Boyer E,Horaud R.Keypoints and local descriptors of scalar functions on 2d manifolds[J].International Journal of Computer Vision,2012,100(1):78-98.

[11]Petrelli A,Stefano LD.On the repeatability of the local refe-rence frame for partial shape matching[C]//IEEE International Conference on Computer Vision.Barcelona:ICCV,2011:2244-2251.