二次重現期在暴雨洪澇災害中的應用研究
范嘉煒, 袁明道, 馬妍博, 潘展釗, 張旭輝
(1.廣東省水利水電科學研究院, 廣東 廣州 510635;2.廣東省大壩安全技術管理中心, 廣東 廣州 510635;3.廣東省山洪災害突發事件應急技術研究中心, 廣東 廣州 510635)
1 研究背景
近年來,受極端水文氣候的影響,我國中南部地區頻繁遭遇強降雨襲擊,加劇了城市以及周邊鄉鎮的內澇問題[1-3]。雖然內澇問題是由多種因素共同作用下而導致的,但短時間內的強降雨是眾多因素中一個最為主要的誘發因素,城市的防洪排澇能力不足以應對暴雨的侵襲,會直接造成城市內澇的發生。當降水集中且強度較大時,加之市區排水設施落后,建設標準不達標等因素,受災情況更為嚴重。內澇的發生給城市的交通運輸、通訊、電力等重要系統帶來了嚴重的破壞,給居民的日常生活造成了諸多不便和影響,巨大的經濟損失遠遠超過由暴雨等極端天氣導致的直接經濟損失[4-5]。
因此,為加強城市防洪減災能力,提升現有城區排水設施標準,倪增華等[6]建立了以年降雨均值和年降雨極值均值為變量的聯合分布,提出在實際工程中采用聯合重現期下的設計值作為防洪排澇標準更安全。曹偉華等[7]指出僅基于單一致災因素的重現期估算會低估致災風險,多因素下的條件重現期更能準確地反映強降雨的致災危險性,為實現防災減災規劃和預警提供科學依據。劉成林等[8]提出了基于降雨特征變量的分析方法,并指出合理確定降雨特征量是防洪排澇系統設計、調度運行的關鍵。劉曾美等[9]提出了基于澇區暴雨和承泄區水位的治澇標準分析方法,并用聯合分布模型描述其遭遇幾率。黃寧[10]以浙江省某城區為研究對象,在分析降雨事件的基礎上,對內澇風險評估方法進行了驗證。
在傳統的水文計算中,通常采用單變量方法估算降雨特征值,忽略了變量間的相關性,顯然這不利于準確評估暴雨致災事件[11],對合理設定城市防洪排澇標準也有較大的影響。本文以以高州市大坡站1967-2016年降雨資料為依據,應用Copula函數[12]和二次重現期理論[13-15],建立不同歷時降雨組合的聯合分布函數,對比分析了傳統重現期和二次重現期值的差異性,并計算了3種重現期法下的設計值,分析結果可為研究區洪澇災害防治工程設計、合理制定防洪排澇標準提供參考依據。
2 研究方法
2.1 G-H Copula函數
Gumbel-Hougaard (G-H) Copula函數屬Archimedean-Copula函數中的一種[12],它能夠將多個變量的邊緣分布聯結起來,反映變量之間的相關關系。目前在水文領域被廣泛應用。Copula函數由于表達形式簡潔易懂,且由于在其構造基于多變量的聯合分布函數時可以變換多種形式,在水利工程中也被廣泛應用于分析實際問題。
Gumbel-Hougaard(G-H)Copula的表達式為:
C(u1,u2)=exp(-((-lnu1)θ+
(-lnu2)θ)1/θ),θ∈[1,∞)
(1)
式中:θ為函數參數;u1和u2為邊緣分布函數。
參數θ的估計通常采用相關性指標法,通過建立Kendall秩相關系數τ與θ的關系推求θ的值。τ與θ的關系可由式(2)表示:
(2)
而τ可由式(3)推求:
(3)
式中:τ為Kendall秩相關系數; sign為符號函數; (xi,yi)為測點據;n為實測序列長度。
2.2 傳統重現期與二次重現期
傳統重現期分為聯合重現期和同現重現期,目前被水文界普遍認可。變量的重現期與它們的聯合分布函數C相關聯,C值越大,說明發生該水文事件的可能性越小,相應的重現期就越大。
若取降雨組合序列P1和P2為研究對象,將邊緣分布函數以式(4)表示:
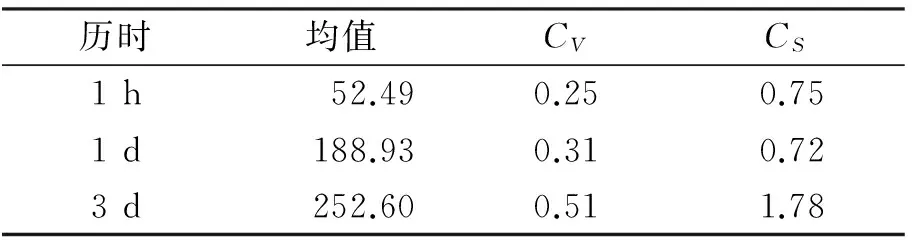
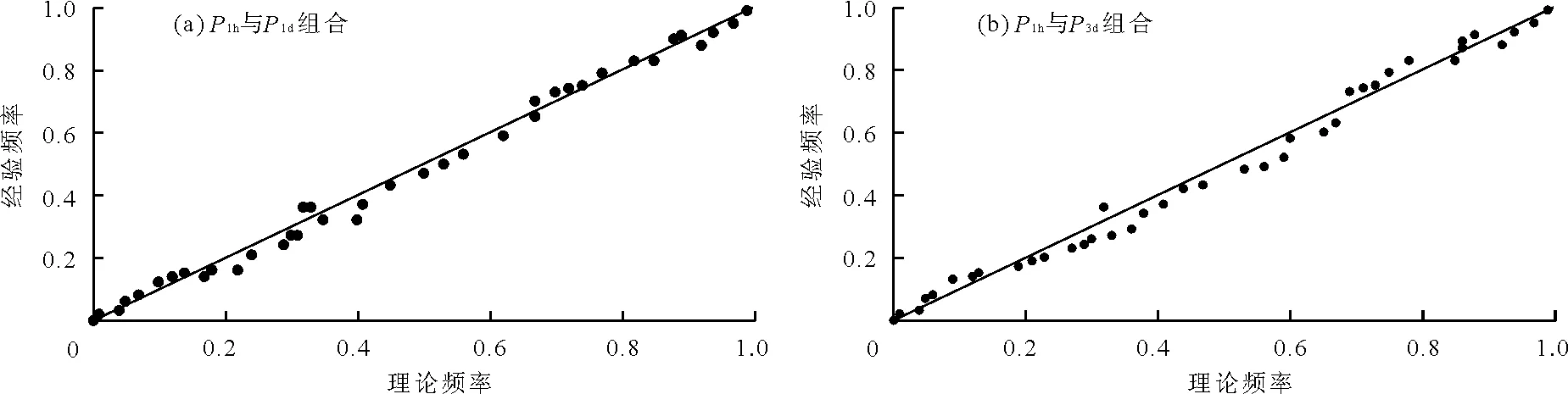
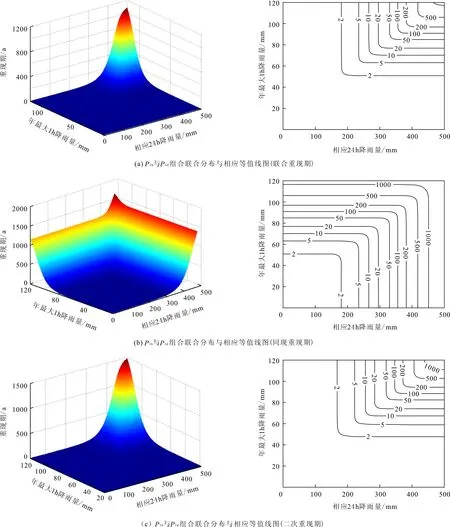
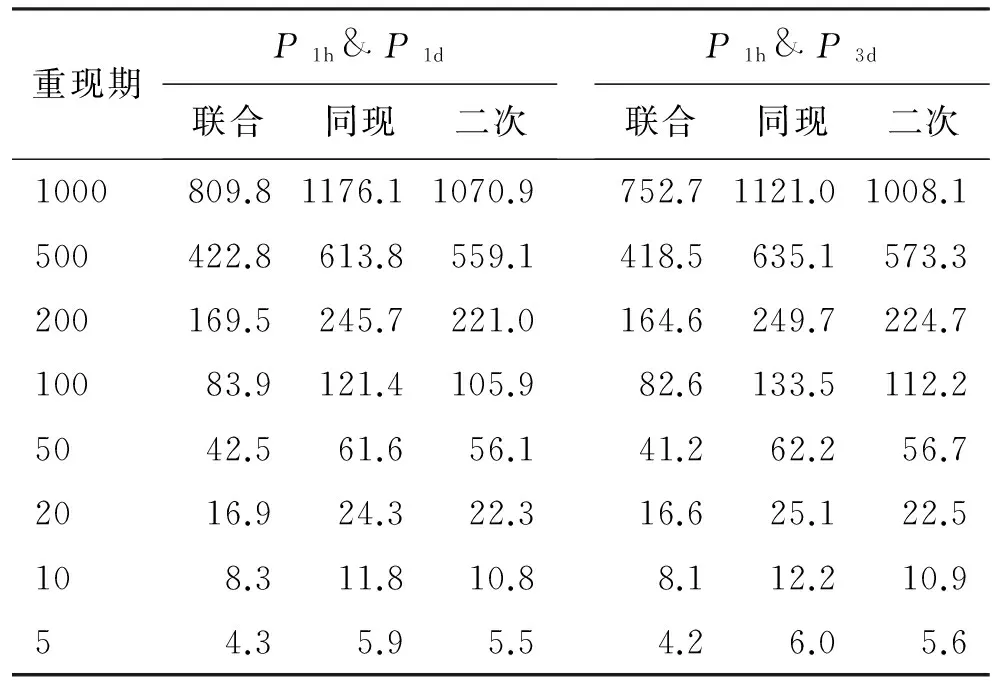
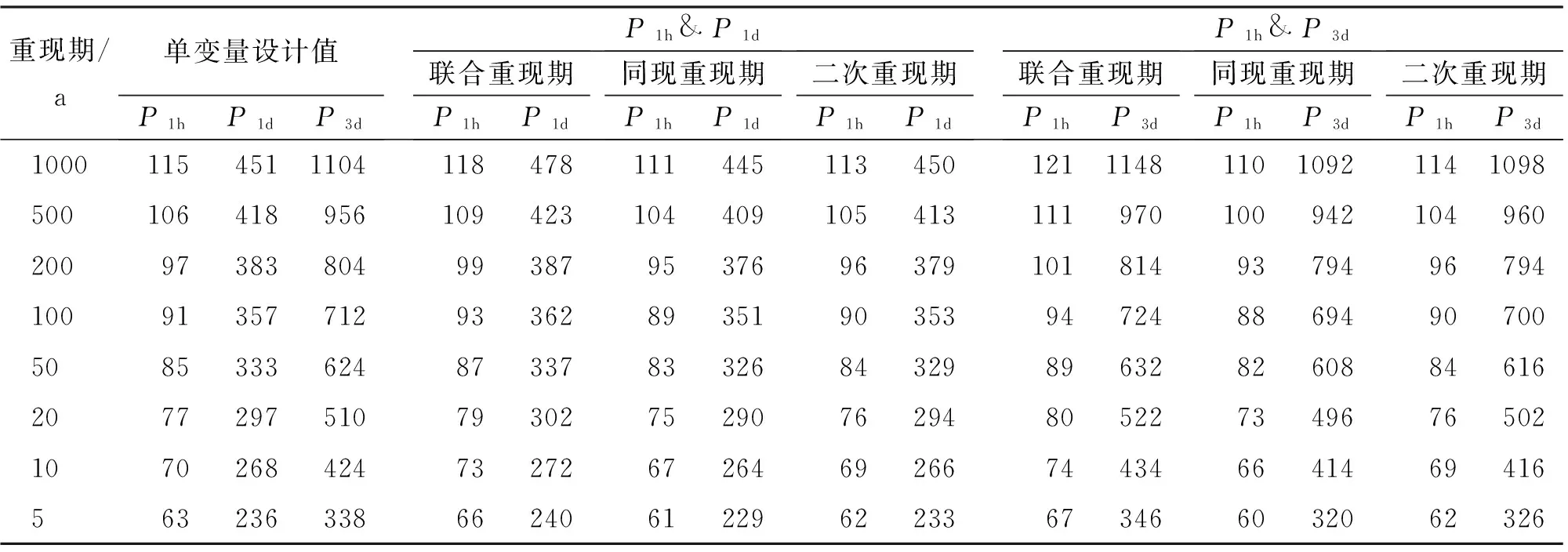
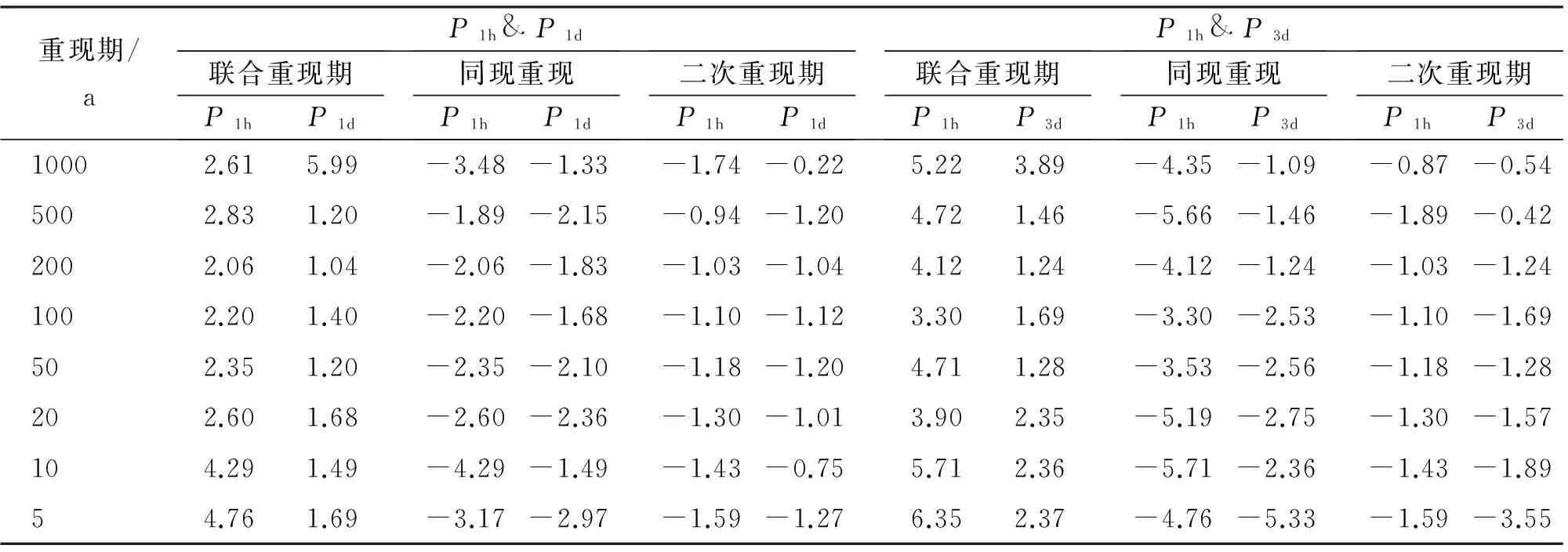
u=f1(x)=P(P1 v=f2(y)=P(P2 (4) 對于P1和P2其中之一超過設定閾值時的工況以式(5)表示;對于P1和P2兩者同時超過設定閾值時的工況以式(6)表示。目前水文界稱兩者為聯合重現期和同現重現期,同屬傳統重現期計算法。P1和P2為設定的閾值,u、v、C(u,v)意義同前: (5) (6) 值得注意的是,目前在水利工程設計中,通常選擇偏保守的聯合重現期確定研究對象的設計值,然而在給定重現期條件下會對應無數多組不同的變量組合,每組變量都可以對應一個危險域[16-17],因此對于相同的重現期值,樣本所對應的危險域和安全域卻不相同,直接導致了危險域之間互相矛盾的現象[17]。顯然,這種定義是有缺陷的。針對同現重現期而言,這個問題依舊存在。考慮到在定義傳統重現期時導致危險域不唯一的情況,SALVADORI[13-15]提出了一種新的定義重現期的方法,將Kendall測度Kc應用在重現期定義中,令聯合概率小于等于t使得多變量分布函數與一維分布相關聯。這種定義方式從根本上解決了傳統重現期法的不合理性,使得變量組合在給定重現期或風險概率情況下有唯一危險域與之對應。函數Kc可用式(7)表達,式中t∈(0,1): Kc(t)=P(W≤t)=P(C(u,v)≤t) (7) Kc測度在Gumbel-Hougaard(G-H)Copula函數中表達形式如下: (8) 式中:θ為G-H Copula參數,φ(t)=[-ln(t)]θ為生成元。 因此結合重現期定義,二次重現期可表達如下: (9) 考慮到二次重現期在定義危險域中的優越性,本文在對高州市暴雨致災事件進行風險評估時采用第二重現期與傳統重現期法分別計算,并就計算的設計值和誤差進行了全面的對比和分析。 以高州市大坡站1967-2016年降雨資料為依據,選取年最大1h降雨并以此時間為基準選取連續1d、3d降雨序列,建立1h~1d、1h~3d降雨組合樣本。樣本數據采用P-Ⅲ型曲線頻率適線,分析結果見表1。 表1 高州市大坡站各時段暴雨頻率表 mm 通過式(3)計算得到P1h&P1d組合的秩相關系數τ為0.454,P1h&P3d組合的秩相關系數τ為0.130,故兩組變量間存在一定的正相關性,故分別建立降雨組合的聯合分布函數,其中函數參數θ由τ-θ關系推求: P1h&P1d:C(u,v)=exp(-((-lnu)1.83+ (-lnv)1.83)1/1.83) (10) P1h&P3d:C(u,v)=exp(-((-lnu)1.15+ (-lnv)1.15)1/1.15) (11) 為了確認G-H Copula函數是否能準確擬合變量間的相關關系,本文采用較為直觀的圖形分析法進行擬合優度評價[18]。該方法將經驗概率和理論概率分別標繪于同一圖中,若當散點均分布在45°線周圍時,則變量組合具有較好的相關性。變量組合的經驗概率值可由Femp(xi1,xi2)表示如下: (12) 式中:N為實測序列的總對數;ni為序列中小于等于(xi1,xi2)的對數。 將以上兩組變量為研究對象計算得出的理論頻率值和式(12)得到的經驗頻率值點繪于圖1中。從圖1可以看出,Gumbel-HougaardCopula構造的兩組降雨序列聯合分布的經驗點值與理論計算值均勻分布在45°線附近,因此G-HCopula擬合效果良好。 由此建立基于G-HCopula函數的降雨組合在3種重現期下的聯合分布模型和對應等值線圖,并以P1h&P1d組合為例,繪于圖2。P1h&P3d聯合分布特征與之相近,篇幅所限,故省略。從圖2可見,聯合重現期和二次重現期的等值線圖的分布特征較相近,當取同樣的降雨組合時,二次重現期的取值略大于聯合重現期,相比而言,同現重現期圖的分布形態較前兩者有較大不同。 根據傳統重現期的定義,在相同的單變量重現期條件下,聯合重現期值一定小于同現重現期,且二次重現期值處于前兩者之間,表2列出的3種重現期法下的降雨組合計算結果也充分反映了這種分布規律。例如在單變量條件下,取P1h和P1d均為200年一遇,則聯合重現期為169.5a,同現重現期為245.7a,二次重現期為221.0a;取P1h和P3d均為1000年一遇,則聯合重現期為752.7a,同現重現期為1 121.0a,二次重現期為1 008.1a。 圖1 理論—經驗頻率擬合圖 圖2 不同重現期下的P1h & P1d組合聯合分布與相應等值線圖 在進行城市內澇防治工程設計中常常需要估算不同重現期下的降雨設計值,這對于合理確定排水管渠尺寸,實現工程效益與工程投資比最大化十分重要。在單變量的水文頻率分析中,在給定的重現期下,存在唯一的設計值與之對應。但在有多個水文變量的情況下,無論重現期大小是否相同,都有無數種可能的設計值組合。由于沒有與概率函數相對應的反函數,因而無法直接獲得設計值。權函數法[17]作為新興的設計方法,可以與聯合分布模型相結合,估算最可能出現的組合設計值: (um,vm)=arc maxf(u,v) (13) f(u,v)=c(u,v)f1(x)f2(y) (14) 式中: (um,vm)為所求降雨設計值組合;c(u,v)、f1(x)、f2(y)意義同前。 表3列出了年最大1h降雨量與連續累積1d和3d降雨組合的設計雨量。從表3中可以看出,單變量降雨設計值分別小于和大于聯合重現期與同現重現期條件下的降雨設計值,例如在P1h&P1d降雨組合下,重現期取500年一遇時,P1d設計值為418mm,小于聯合重現期下的設計值423mm,大于同現重現期下的設計值409mm,而基于二次重現期的設計值為413mm介于以上兩者之間且略小于單變量設計值,因此可以起到既滿足防洪排澇設計要求,又可以降低工程經濟成本的作用。 設計值的分布規律可簡要概括為聯合重現期>單變量重現期>二次重現期>同現重現期。出現以上分布規律的原因是由于聯合重現期法擴大了事件的危險域,致使在同樣的降雨組合下得到的危險事件發生的重現期較小,在相同的重現期條件下降雨組合的設計值較大;而同現重現期則與之相反,它縮小了事件的危險域,過高估計了危險事件的重現期,采用此方法會使降雨設計值偏小。 表2 不同歷時降雨組合的3種重現期 a 表3 不同重現期下的降雨組合設計值 mm 表4列出了以P1h&P1d和P1h&P3d降雨組合為例,3種重現期設計值與單變量重現期設計值的誤差。在P1h&P1d中,二次重現期的估算誤差絕對值范圍為0.22%~1.74%,最大誤差均出現在重現期1 000a;聯合重現期和同現重現期誤差范圍分別為1.04%~5.99%、1.33%~4.29%。在P1h&P3d中,二次重現期的估算誤差絕對值范圍為0.42%~1.89%,同樣較聯合與同現法誤差為小。 表4 降雨組合設計值與單變量重現期設計值誤差 % (1)工程設計中常常需要估算不同重現期下的降雨設計值,在考慮多個水文變量的條件下,會出現無數種可能的設計值組合。權函數法作為新興的設計方法,可以與聯合分布模型相結合,估算最可能出現的組合設計值。 (2)以年最大1h降雨與連續累積1d和3d降雨量為降雨組合,推求了基于3種重現期法下的重現期設計值與降雨設計值,通過對比和分析指出二次重現期能夠有效避免對水文事件危險域過大或過小的估計。 (3)兩種傳統重現期方法由于受各自定義特點的約束,造成了在考慮危險事件時對重現期和設計值的估算出現偏差。但在一些有指定設計要求的工程中,可利用傳統方法定義明確這一特點,結合“或”和“且”的設計理念,合理選擇最佳的估算方法。在無特定要求的工程設計中,為了盡可能真實地反映降雨事件的實際特征,一般推薦采用基于二次重現期法的估計值。 (4)聯合重現期估計設計值過大,在工程建設中偏保守,將造成施工費用偏高;同現重現期法估計的設計值過小,雖然造價較為經濟,但在工程建設中存在風險。因此,為了經濟合理地實施城市基礎設施建設,實現防洪排澇能力最大化和施工成本最小化,二次重現期法可以作為確定排澇管渠規格等工程設計的重要參考。 [1]FONTANAZZACM,FRENIG,LALG,etal.Uncertaintyevaluationofdesignrainfallforurbanfloodriskanalysis[J].WaterScience&Technology(AJournaloftheInternationalAssociationonWaterPollutionResearch), 2011,63(11):2641-2650. [2]IPCC.Climatechange2007:Synthesisreport[M].Cambridge:CambridgeUniversityPress,2007. [3] 陸桂華,張亞洲,肖 恒,等.氣候變化背景下蚌埠市暴雨與淮河上游洪水遭遇概率分析[J].氣候變化研究進展,2015,11(1):31-36. [4] 郭常安,鄧立鳴.廣州市中心城區內澇分析及對策[J].中國給水排水,2011,27(10):25-28. [5] 莫建飛,陸 甲,李艷蘭,等.基于GIS的廣西農業暴雨洪澇災害風險評估[J].災害學,2012,27(1):38-43. [6] 倪增華,劉合香,羅彥麗,等.Copula函數在廣西洪澇災害的降水概率預測中的應用[J].氣象研究與應用,2014,35(2):32-39. [7] 曹偉華,梁旭東,趙晗萍,等.基于Copula函數的北京強降水頻率及危險性分析[J].氣象學報,2016,74(5):772-783. [8] 劉成林,周玉文,隋 軍,等.設計降雨特征的多變量分析方法[J].北京工業大學學報,2015,41(6):940-945. [9] 劉曾美,陳子燊.基于兩個致災因子的治澇標準研究[J].水力發電學報,2011,30(3):39-40+49. [10] 黃 寧.降雨事件聯合概率分析及其在城市內澇風險評估中的應用[D].杭州:浙江大學,2016. [13]SALVADORIG,MICHELECD.Multivariatemultiparameterextremevaluemodelsandreturnperiods:AcopulaApproach[J].WaterResourcesResearch,2010,46(10):219-233. [14]SALVADORIG,MICHELEC.Ontheuseofcopulasinhydrologytheoryandpractice[J].JournalofHydrologicEngineering,2007,12(4):369-380. [15]SALVADORIG.Bivariatereturnperiodsvia2-copulas[J].StatisticalMethodology,2004,1(1-2):129-144. [16] 史黎翔,宋松柏.基于Copula函數的兩變量洪水重現期與設計值計算研究[J].水力發電學報,2015,34(10):27-34. [17] 范嘉煒,黃錦林.基于Kendall重現期的降雨潮位風險分析[J].水電能源科學,2017,35(5):21-24+20. [18] 范嘉煒,黃錦林.基于Copula函數的洪峰流量與洪水歷時聯合分布研究[J].中國農村水利水電,2017(2):204-209+214 .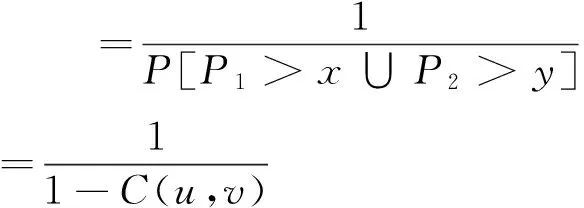
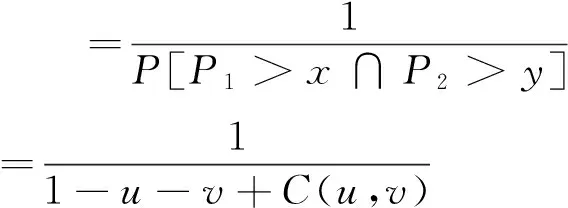
3 研究區域分析
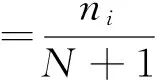
4 結 論