樓層側向剛度比對砌體結構地震易損性的影響分析1

趙文哲 溫增平 徐 超 陳 波

1）中國地震局地球物理研究所，北京 100081

2）中石化廣州工程有限公司，廣州 510000

引言

控制建筑結構抗側力系統(tǒng)的剛度變化是結構抗震設計的重要內容。結構的損傷、修復以及結構物用途的改變，都會引起結構樓層剛度的變化。在地震作用下，結構豎向剛度的變化容易導致薄弱層出現(xiàn)，引起結構抗震性能的退化。砌體結構廣泛存在于我國城鎮(zhèn)、農村地區(qū)，且普遍存在豎向剛度不規(guī)則現(xiàn)象。近年來，多次工程震害現(xiàn)象表明一些砌體結構在設計上存在缺陷，如結構豎向剛度不均勻，導致薄弱層的出現(xiàn)，造成房屋結構嚴重破壞甚至倒塌。汶川8.0級和蘆山7.2級地震的砌體結構震害特征中，結構平面和立面布置不規(guī)則現(xiàn)象較為常見，特別是二層結構外挑的多層砌體結構，豎向剛度存在突變，結構物“頭重腳輕”，引起結構底層嚴重破壞。此外，我國農村地區(qū)許多自建的砌體結構，開洞過多且位置布局不合理，造成結構抗側剛度不足，在地震作用時出現(xiàn)應力局部集中，加重了結構的破壞程度（李小軍等，2008；溫增平等，2009；徐超等，2013）。尤其對于由砌體材料建造的教學樓，為滿足其功能要求，結構開間和進深較大，因其采光和通風的需要，縱墻設置較多門窗，這使得結構抗側剛度變化，在地震中破壞較為嚴重（周強等，2010）。

針對上述工程震害調查中豎向剛度不規(guī)則砌體結構呈現(xiàn)的破壞現(xiàn)象，學者們展開了一系列對豎向剛度不規(guī)則砌體結構抗震性能的研究。孫柏濤等（2012）對豎向變剛度約束砌體結構進行數(shù)值模擬，發(fā)現(xiàn)剛度由下到上逐漸變小的砌體結構抗震能力有一定程度提高；劉紅彪（2012）通過兩棟開洞較多砌體結構的振動臺倒塌對比實驗分析，得出結構層間同方向各墻體抗側剛度應基本相等，對于開洞較大墻體設置構造柱可以使地震剪力在各墻段分配均勻，結構的抗震能力得到一定提高；劉硯山等（2013）研究了不同側向剛度比對底框砌體結構抗震性能的影響，發(fā)現(xiàn)適當增大底層抗震墻剛度可以提高結構的抗震性能；孫雷等（2013）對單層層高超限、設置大開間的典型村鎮(zhèn)自建豎向不規(guī)則砌體房屋進行數(shù)值模擬，發(fā)現(xiàn)抗震構造措施可以顯著改變砌體結構動力特性，芯柱和墻體協(xié)同工作機制可以向弱框架結構轉化，對結構抗震性能產生影響；孫柏濤等（2015）以汶川地震中1棟破壞嚴重的底框砌體結構為例，通過有限元分析發(fā)現(xiàn)，裙房對主體結構剛度影響較大，加劇了結構的地震反應，建議在結構設計時裙房和主體結構采用抗震縫隔開。

國內學者對砌體結構地震易損性做了大量的研究工作。楊玉成等（1982）對多層房屋結構易損性及其震害預測開展過研究；高小旺等（1990）研究了在不同烈度下砌體結構超越不同破壞狀態(tài)的概率；張令心（2002）采用非線性時程分析研究了多層砌體結構地震易損性，計算了在不同烈度下多層砌體結構的易損性曲線；熊立紅等（2003）對2棟新型砌塊房屋進行非線性時程分析，研究了砌體房屋在抗震設防“三水準”下的結構出現(xiàn)不同破壞狀態(tài)的概率。這些研究成果主要是針對規(guī)則砌體結構開展的地震易損性分析。

目前，針對豎向剛度不規(guī)則性對砌體結構地震易損性影響的研究較少，但在我國城鎮(zhèn)及農村，許多自建的砌體結構普遍存在抗側剛度不均勻的情況，當在這些地區(qū)開展震害預測時常常需要分析不規(guī)則的砌體結構易損性。為了考慮豎向剛度不規(guī)則性對砌體結構地震易損性影響，本文定量研究了樓層側向剛度變化對結構超越不同破壞狀態(tài)概率的影響，以3層和6層典型砌體結構為例，采用等效多自由度層間剪切模型，基于增量動力法（Incremental Dynamic Analysis，IDA）及回歸擬合分析，建立結構地震易損性曲線。通過改變結構樓層側向剛度分布形式來模擬薄弱層，分析了樓層剛度突變對結構不同破壞狀態(tài)超越概率的影響。通過改變底層與二層側向剛度比，研究了剛度變化對結構不同破壞狀態(tài)超越概率的影響。

1 基于IDA方法的砌體結構地震易損性

1.1 結構易損性模型

在易損性分析中，通常采用對數(shù)正態(tài)分布作為易損性概率模型（Singhal等，1996；Shinozuka等，2000），基于地震動參數(shù)的易損性可表示為：

由對數(shù)正態(tài)分布的性質可知，自然對數(shù)的均值等于中值的自然對數(shù)，則式（1）可表示為：

式中，IM為描述地震動強度的隨機變量；IMc為達到不同破壞狀態(tài)時的地震動強度；F（IM）為易損性函數(shù)；Φ為標準正態(tài)分布累計函數(shù)。μln（IMc）、ηIMc、βIMc分別為隨機變量IMc的對數(shù)均值、中值和對數(shù)標準差，一般可以根據(jù)結構動力反應分析結果及回歸擬合方法進行確定。

1.2 基于IDA的砌體結構地震反應分析

IDA作為1種有效的地震易損性分析方法，已廣泛應用于不同結構類型的易損性分析（Vamvatsikos等，2002）。IDA曲線反應了結構響應參數(shù)與地震動參數(shù)之間的聯(lián)系。本文選用結構地震響應值（最大層間位移角θmax）為曲線縱坐標，選用地震動輸入?yún)?shù)（峰值加速度PGA）為橫坐標。

Vamvatsikos等（2002）研究表明，采用20條地震記錄作為地震動輸入可以很好地反映地震動的不確定性。本文從美國太平洋地震中心選擇21條地震記錄，震級分布為6—8級，PGA≥0.05g，VS30分布區(qū)間為210—510m/s，場地條件大致相當于我國Ⅱ類場地。挑選的地震動記錄見表1，其加速度反應譜見圖1，黑色實線為50%分位線。

表1 選擇的地震動記錄Table 1 Selected records of ground motion

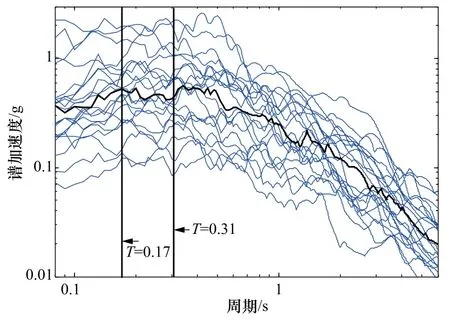
圖1 挑選的地震動的加速度反應譜Fig.1 The acceleration response spectrum of selected ground motion

以所選的地震記錄作為輸入對結構進行IDA分析，可得到結構的動力反應值，砌體結構最大層間位移角與峰值加速度對應關系的IDA分析結果，如圖2所示。研究表明，在給定強度地震動作用下，可認為結構的反應服從對數(shù)正態(tài)分布（Shome，1999），因此可采用對數(shù)線性概率地震需求模型建立結構反應與地震動參數(shù)之間的統(tǒng)計關系：

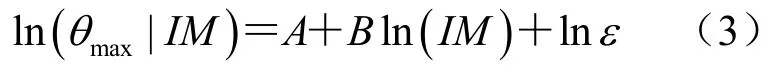
式中，θmax|IM為給定強度IM地震動作用下的結構最大層間位移角。A、B為回歸系數(shù)，ε為估計誤差。

采用μln(θmax|IM)表示 ln(θmax|IM)均值、ηθmax|IM表示θmax|IM中值、βθmax|IM表示 ln(θmax|IM)標準差，則有：

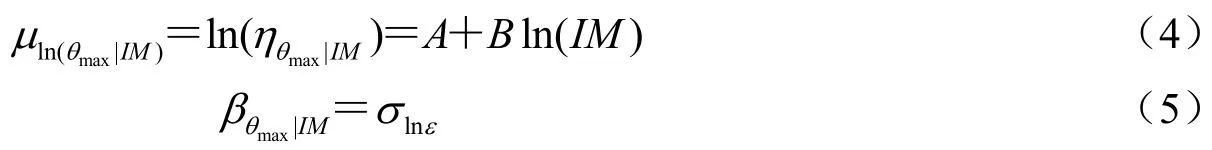
基于式（3）對圖2中的砌體結構反應與地震動參數(shù)進行回歸擬合，可確定回歸系數(shù)A、B及擬合標準差σlnε，示意圖如圖3所示。

圖2 地震作用下砌體結構的IDA響應Fig.2 IDA respond of masonry structure

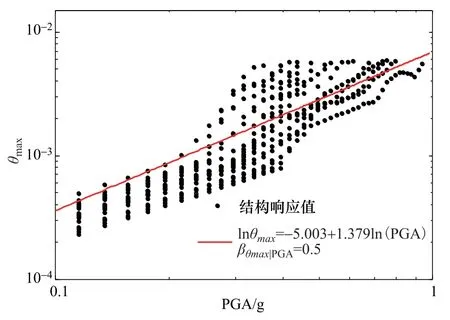
圖3 砌體結構動力反應值與地震參數(shù)對數(shù)擬合結果Fig.3 Logarithmic fitting results of dynamic response and seismic parameters of masonry structure

1.3 不同破壞狀態(tài)對應的層間位移角限值

結構物破壞等級通常可分為5類（中華人民共和國國家質量監(jiān)督檢驗檢疫總局，中國國家標準化管理委員會，2009），分別為“基本完好”、“輕微破壞”、“中等破壞”、“嚴重破壞”和“倒塌”，用DSk（k＝0，1，……，4）對應表示。

采用層間位移角作為變形指標對砌體結構的破壞等級進行劃分。夏敬謙等（1988）和熊立紅（2004）通過對砌體墻體進行大量試驗，給出了不同破壞狀態(tài)對應的最大層間位移角限值(θmax|DS)的參考均值，其變異系數(shù)δθmax|DS取0.35（莊一舟等，1999）。

一般可以認為結構不同破壞狀態(tài)對應的最大層間位移角限值服從對數(shù)正態(tài)分布，根據(jù)對數(shù)正態(tài)分布的性質，可采取式（6）、（7）計算不同破壞狀態(tài)對應的層間位移角限值的中值ηθmax|DS和對數(shù)標準差βθmax|DS，進而得到其概率分布參數(shù)（表2）。

表2 層間位移角限值Table 2 Allowable value of story drift ratios

1.4 易損性曲線的生成

以結構反應參數(shù)為中間變量，易損性也可表示為：

由前文可知，θmax|IM和θmax|DS均服從對數(shù)正態(tài)分布且相互獨立，則－為正態(tài)分布隨機變量，其統(tǒng)計參數(shù)分別為：

則易損性函數(shù)可以表示為：

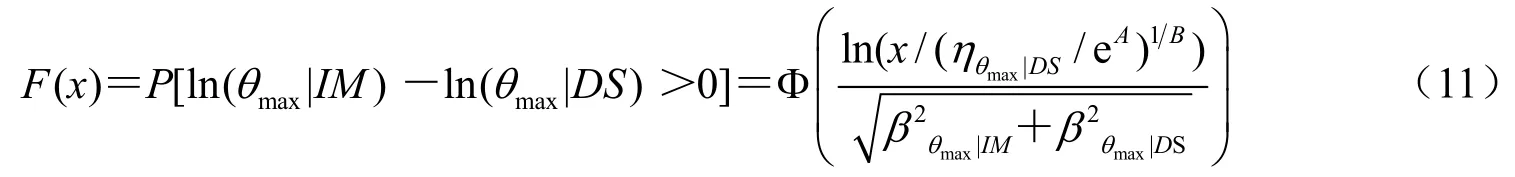
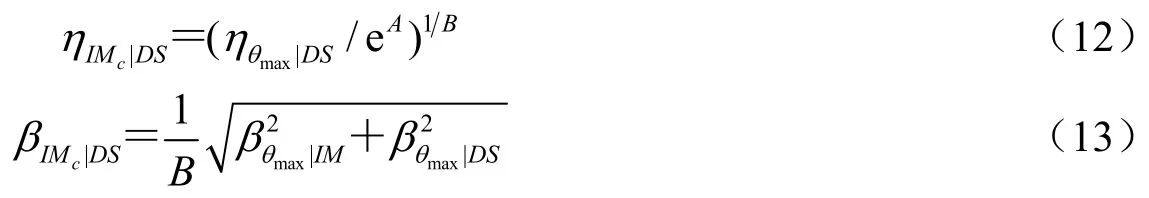
2 結構模型

2.1 建筑概況

以3層和6層典型砌體結構為例，結構設防烈度Ⅶ度，設計場地為Ⅱ類。采用燒結黏土磚，等級MU15，砂漿強度等級M5。3層砌體層高均為3m，縱橫墻承重，墻厚均為240mm。6層砌體層高均為2.7m，外墻厚370mm，內墻厚240mm。屋面均采用120mm厚混凝土樓板，選用C20混凝土。樓面活荷載3.5kN/m2，屋面活荷載4.5kN/m2。構造符合《砌體結構設計規(guī)范》（中華人民共和國住房和城鄉(xiāng)建設部，2012）要求。在橫墻與縱墻交會、外墻轉角以及開間大于4.2m的位置設置構造柱，截面尺寸240mm×240mm，縱向配筋4Φ14，箍筋Φ6@150mm。結構布置圖如圖4所示。

圖4 結構布置Fig.4 Structure layout

2.2 計算模型

由于砌體結構高寬比較小，在地震作用下易表現(xiàn)出較為明顯的剪切破壞。可以采用多自由度層間剪切模型對結構進行非線性時程分析（Xiong等，2016）。通常認為砌體結構樓板剛度無限大且忽略樓板轉動位移，該模型將每層簡化為1個質點，將每層的質量都集中在樓面上。多自由度層間剪切模型的示意圖如圖5所示，其中c1、c2、c3為樓層阻尼，m1、m2、m3為樓層等效質量，k1、k2、k3為示意的樓層等效剛度。動力分析選用考慮剛度退化的三線性恢復力模型（劉錫薈等，1981），該模型有4個獨立參數(shù)Vy、Vp、K0、K1，見圖6，其中Vy、Vp分別代表屈服荷載、極限荷載，xy、xp分別代表屈服位移、極限位移，K0為初始剛度，K1為硬化剛度，K2為卸載剛度，K3為軟化剛度。

對于砌體結構而言，結構的橫向和縱向抗震性能有所不同，縱向墻體開洞較多結構抗震性能較差（林旭川等，2008），本文主要對結構縱向進行非線性時程分析。

圖5 層間多自由度剪切模型示意圖Fig.5 Multi-story concentrated-mass shear model for a building

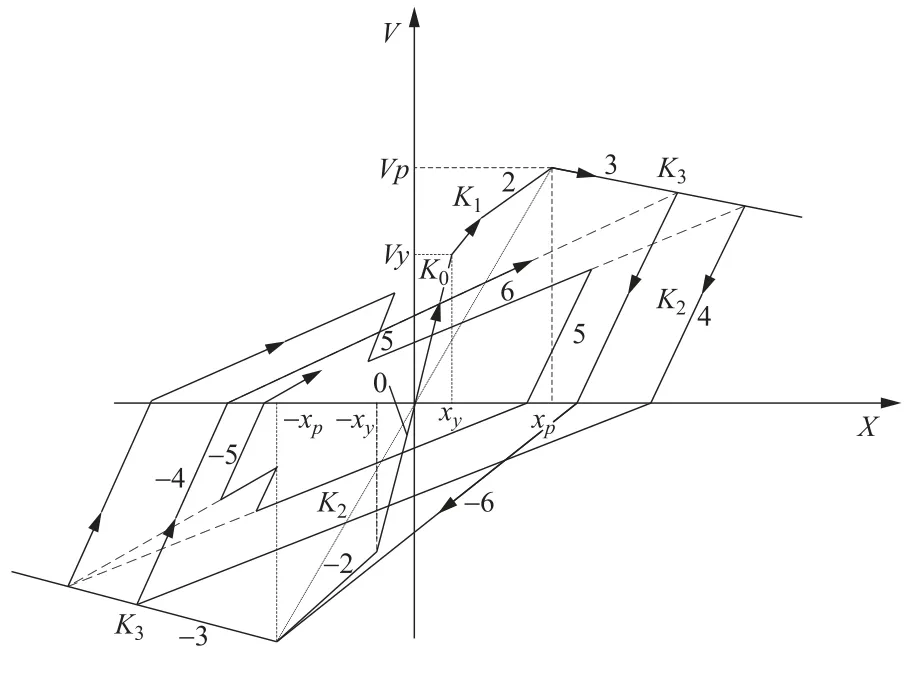
圖6 恢復力模型Fig.6 Restoring force model

2.3 恢復力模型參數(shù)標定

劉錫薈等（1981）對帶構造柱的磚墻足尺墻片進行側向往復荷載加載實驗，建立了砌體結構合理的滯回模型，給出了恢復力模型參數(shù)標定的方法；并選擇2棟典型砌體結構進行對比驗證，計算結果與實驗結果擬合良好。《設置鋼筋混凝土構造柱多層磚房抗震技術規(guī)程》（中華人民共和國建設部，1994）和張令心等（2002）對該恢復力模型進行進一步修正，給出了其恢復力參數(shù)的確定方法。

2.3.1 墻體抗側移剛度

初始剛度的計算公式為：

其中，G為磚砌體剪切模量（MPa）；Am為墻段水平截面總面積（m2）；ξ為剪力不均勻影響系數(shù)，矩形取1.2；h為墻段計算高度（m）；λ0為墻段考慮開孔和彎曲影響的剛度修正系數(shù)，當墻的高寬比h/b≤1時，

當1≤h/b≤4時，

其中，Az表示墻段內混凝土構造柱的水平截面積之和（m2）；Ajz為墻段扣除混凝土構造柱后的砌體水平截面積（m2）；Ec為混凝土彈性模量（MPa）；E為砌體彈性模量（MPa）；η0為構造柱鋼筋參與墻體的工作系數(shù)，η0＝0.26；I為構造柱折算后與墻凈截面一起計算的慣性矩（m4）；Ac為構造柱水平向截面面積（m2）；φ0為開洞影響系數(shù)（中華人民共和國住房和城鄉(xiāng)建設部，2012）。

硬化剛度K1＝αK0，考慮構造柱影響時α取0.075。

2.3.2 墻段截面強度

屈服強度表示為：

極限強度表示為：

其中，τk,X為砌體沿灰縫抗剪強度（MPa）；σ0為首層墻段中間高度平均壓應力（MPa）；A為墻段凈截面面積（m2）。

3 砌體結構地震易損性分析結果

分別對3層和6層規(guī)則砌體結構進行增量動力分析，結合公式（3）得到回歸系數(shù)A、B，見表3。帶入公式（8）、（9）和（10）得到易損性曲線雙參數(shù)和，擬合結構易損性曲線，如圖7所示。圖中LS1、LS2、LS3和LS4分別代表結構處于輕微破壞、中等破壞、嚴重破壞和接近倒塌4種破壞狀態(tài)的超越概率曲線，6-LS1表示6層砌體結構達到輕微破壞的超越概率曲線，以此類推。

為驗證本文易損性結構的實用性，選用孫柏濤等（2014）給出的設防磚混結構的震害矩陣（表4）與得到的規(guī)則結構易損性曲線進行對比。根據(jù)中國地震烈度（中華人民共和國國家質量監(jiān)督檢驗檢疫總局，2009）給出的烈度與PGA的對應關系，將震害矩陣與易損性曲線繪制同一圖中，見圖7。

從圖7中可以看出，計算得到的砌體結構易損性曲線與統(tǒng)計得到的震害矩陣結果基本一致，超越概率最大相差10%以內。鑒于地震烈度與PGA對應關系存在較大的不確定性，群體結構震害調查與單體結構地震易損性計算相比也有較大的不確定性，超越概率最大相差10%可以接受，故本文方法可以較為精確地計算結構的地震易損性。

表3 規(guī)則結構回歸系數(shù)A、BTable 3 Regression coefficients A, B of regular structures

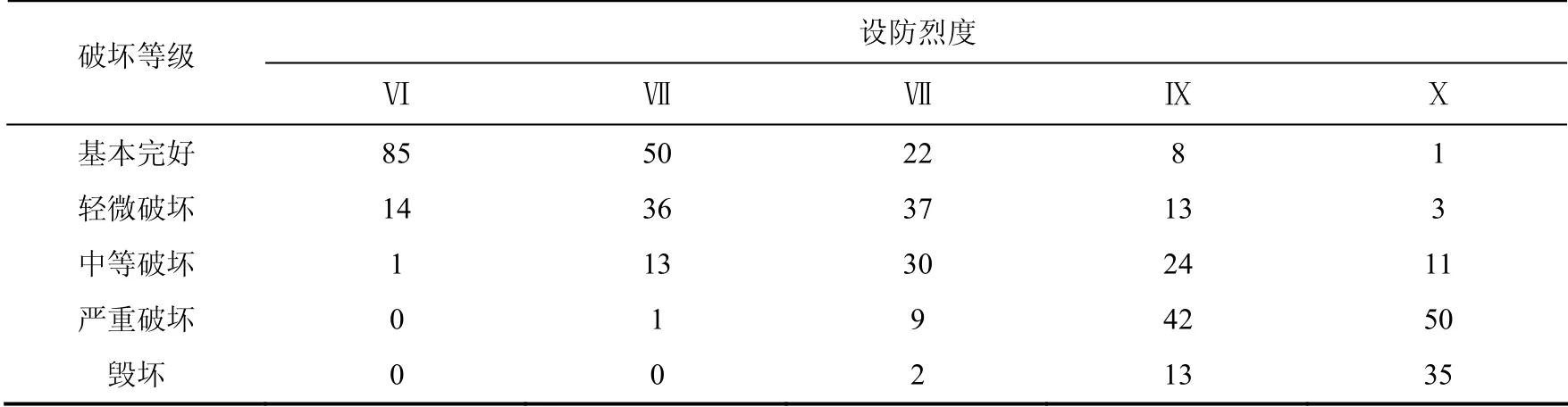
表4 設防磚混結構震害矩陣Table 4 Earthquake damage matrix of fortified masonry structures

3.1 樓層側向剛度突變對砌體結構易損性的影響

建筑結構抗震規(guī)范將結構上下層剛度比為0.5時定義為嚴重不規(guī)則結構。為研究豎向不同位置剛度變化對砌體結構易損性的影響，在其它層剛度保持不變的情況下，逐次將結構每層的剛度折減50%，通過人為控制剛度變化的位置，運用增量動力分析得到不同位置剛度變化時結構的動力反應，通過公式（3）對IDA結果做回歸分析得到回歸系數(shù)A、B，見表5表。將回歸系數(shù)代入公式（8）、（9）得到易損性曲線雙參數(shù)和擬合結構易損性曲線，如圖8所示。1.st-LS1表示第1層出現(xiàn)剛度突變時結構達到輕微破壞的超越概率曲線，以此類推。

由圖8可以看出：①對于3層結構，剛度變化位于第1層時，隨著地震動強度的增加結構超越不同破壞狀態(tài)的概率上升幅度最大。以倒塌破壞狀態(tài)為例（圖8（g）），首層與規(guī)則結構對應的倒塌破壞狀態(tài)超越概率相比最大增長幅度達到41%。②對于6層結構，底部2層剛度突變對結構易損性的影響規(guī)律基本相同，都會增加整體結構的易損性。對于倒塌破壞狀態(tài)而言，首層與規(guī)則結構對應的倒塌破壞狀態(tài)超越概率相比最大增長幅度也超過40%，與第2層出現(xiàn)剛度變化對應的倒塌破壞狀態(tài)超越概率相比最大增長幅度不足10%。第3層出現(xiàn)剛度變化與底部2層出現(xiàn)剛度變化相比，結構輕微破壞對應的易損性曲線基本重合；結構嚴重破壞和倒塌破壞易損性明顯低于底部2層出現(xiàn)剛度變化的情況。此外，當剛度變化出現(xiàn)在結構第4層以上時，其對結構的易損性影響較小，結構第4、5層出現(xiàn)剛度突變對應的嚴重破壞和倒塌破壞狀態(tài)易損性曲線基本重合。但是結構頂層剛度突變對應的易損性比第4、5層剛度突變時更高，這是因為頂層剛度突變造成了鞭梢效應，加重了結構頂層的破壞程度。③與規(guī)則結構相比，6層結構第4、5、6層出現(xiàn)剛度突變時，在給定地震動強度下破壞概率相差較小；3層結構頂層剛度變化和規(guī)則結構倒塌破壞狀態(tài)曲線基本重合。說明結構頂部剛度減小對結構易損性的影響較小。

圖7 震害資料統(tǒng)計結果與砌體結構基于PGA的易損性曲線對比Fig.7 Comparison of statistical data of earthquake disasters and fragility curves of masonry structure based on PGA

圖8 砌體結構基于PGA的易損性曲線Fig.8 Fragility curve of masonry structure based on PGA

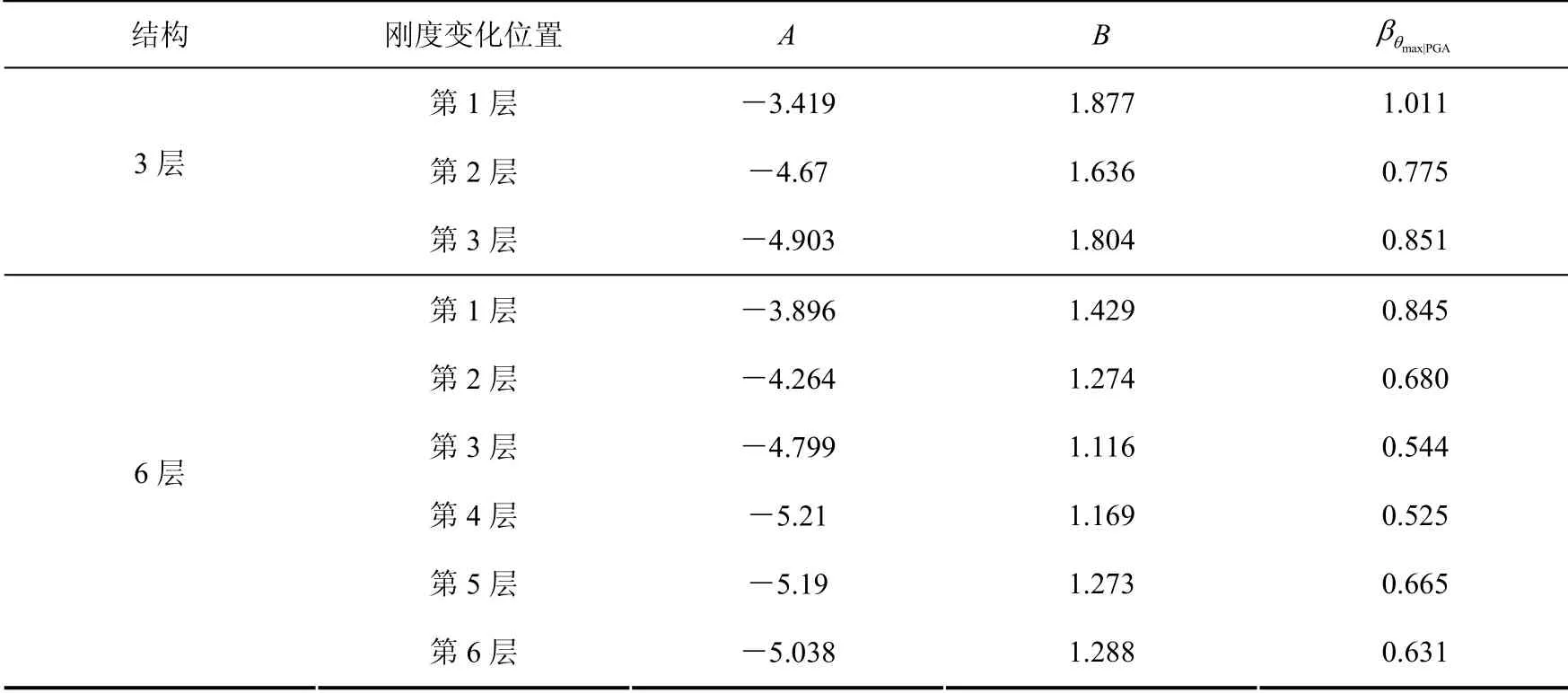
表5 回歸系數(shù)A、B的值Table 5 Regression coefficients A, B

3.2 不同樓層剛度比對砌體結構易損性影響

結構底部2層剛度變化對結構易損性影響較大。為了進一步研究結構剛度過渡區(qū)，即首層與相鄰層（第2層）剛度比（K1/K2）的變化對結構易損性的影響，依次選擇剛度比為0.5、0.7、1、1.2、1.5的3層和6層砌體結構，對其進行非線性時程分析，得到對應的易損性曲線雙參數(shù)和并擬合易損性曲線，如圖9所示。

由圖9可以看出：①對于3層和6層結構，隨著剛度比從0.5增加到1.2，在相同地震動強度下結構超越不同破壞狀態(tài)的概率逐漸減少，結構易損性逐漸降低。②當剛度比增加到1.5時，在強地震動作用下結構出現(xiàn)了薄弱層的轉移，結構的易損性較剛度比1.2時明顯增加。以6層結構為例，當PGA調幅至0.4g時，選取其中9條地震記錄對應的地震反應分析結果，得到結構剛度比為1.2和1.5時不同樓層的最大層間位移角（圖10）。剛度比為1.2時，結構底層較第2層最大層間位移角稍大，結構底層破壞較重，薄弱層位于第1層；剛度比為1.5時，結構第2層變形明顯大于其它樓層，薄弱層出現(xiàn)在第2層。③當剛度比小于1時，剛度比增加對結構對應的倒塌破壞易損性曲線影響明顯；當剛度比大于1時，剛度比變化對倒塌破壞狀態(tài)易損性曲線的影響較小。以圖9（h）為例，剛度比從0.5增加到0.7倒塌破壞狀態(tài)易損性曲線幅度最大下降約20%，從0.7增加到1時，其下降幅度最大超過20%，當剛度比增大至1.2時，其下降幅度只有10%左右。這表明結構底層剛度不宜小于相鄰層剛度，結構剛度宜從下到上由大到小均勻變化。

圖9 不同剛度比對應的結構易損性曲線Fig.9 Fragility curves of masonry structure corresponding to different stiffness ratios

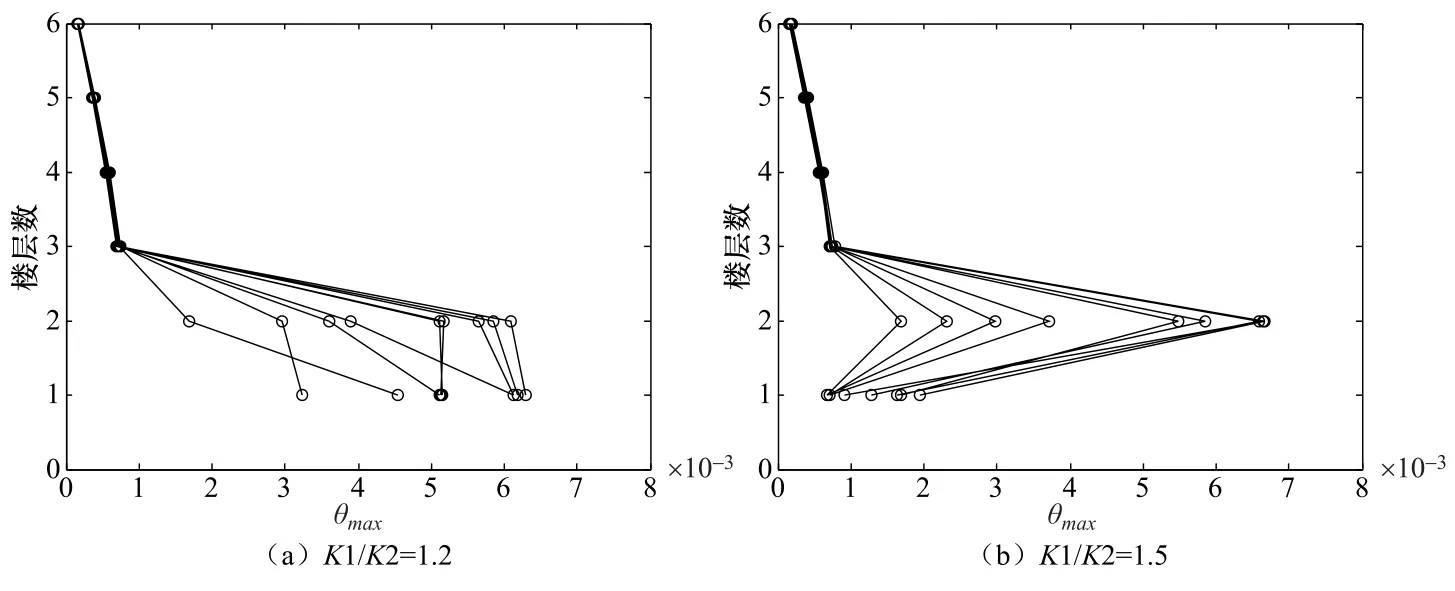
圖10 PGA輸入為0.4g時各樓層最大層間位移角Fig.10 Maximum interstory drift with the input of PGA is 0.4g

4 結論

本文以3層和6層典型砌體結構為例，采用層間剪切模型，借助增量動力法及回歸擬合開展了基于峰值加速度的易損性分析，建立了結構地震易損性曲線。通過改變樓層的側向剛度值模擬薄弱層，定量分析了樓層剛度變化對結構不同破壞狀態(tài)超越概率的影響。通過改變底層與二層的側向剛度比，定量研究了底部剛度突變對結構不同破壞狀態(tài)超越概率的影響。研究得到以下幾點認識：

（1）結構底層出現(xiàn)剛度突變對結構的易損性影響最為顯著。與規(guī)則結構相比，首層剛度突變會明顯增加結構的易損性。以倒塌破壞狀態(tài)為例，3層和6層結構底層剛度突變都可導致其超越概率增加40%左右。結構上部出現(xiàn)剛度突變對結構易損性的影響不明顯。對于6層結構，頂層出現(xiàn)剛度變化時容易出現(xiàn)鞭梢效應，會一定程度加重結構頂層破壞。

（2）在一定范圍內，隨著結構底層與二層側向剛度比的增大（K1/K2從0.5增加至1.2），結構的易損性降低。但是側向剛度比過大（K1/K2＝1.5），會造成薄弱層位置的轉移，結構易損性增加。當?shù)讓优c二層側向剛度比從0.7增加到1時，結構倒塌易損性的降低幅度最多超過20%。當?shù)讓优c二層側向剛度比從1.0增大至1.2時，結構倒塌易損性下降幅度只有10%左右。通過合理控制側向剛度比值，可以一定程度上降低結構的易損性，結構剛度宜由大到小、從下到上均勻變化。