云環境下基于L-BFGS的協同過濾算法

金 淳，何世福

(大連理工大學 管理與經濟學部 系統工程研究所，遼寧 大連 116024)

0 引 言

為解決數據量的快速增長帶來嚴峻的數據稀疏性問題[1]，一些研究通過填充未評分項目值[2,3]、SVD[4-6]等矩陣分解和聚類[7-9]等方法對協同過濾算法改進，但存在填充后數據量極大增加導致的計算資源消耗，或縮減評分數據集帶來評分預測精度降低的問題。因子分解機模型[10](簡稱FM模型)使用矩陣分解的思想，將多項式參數分解成為兩個輔助向量，考慮了特征組合問題，對稀疏數據有良好學習能力和較高的預測精度。為解決數據維度、用戶和商品特征數目的增加帶來推薦算法可擴展性問題，目前主要使用數據集縮減[11]、增量更新[12,13]和矩陣分解[14]等方法來提取較小的數據集，但這些方法在海量數據情況下的迭代次數增多、計算矩陣的指數級增長，計算效率較低。L-BFGS(limited-memory BFGS)[15-17]是擬牛頓法的一種，核心思想為存儲和使用最近的若干次迭代計算的向量序列來構造Hessian矩陣的近似矩陣，具有收斂速度快和占用計算空間低等特點。而FM使用傳統方法進行參數訓練收斂速度較慢，使用L-BFGS算法進行參數訓練可以彌補此缺點，使算法具有良好的可擴展性。

綜上，本文提出基于L-BFGS優化的協同過濾推薦算法(L-BFGS-CF)。該算法使用FM模型進行評分預測，L-BFGS算法作為FM模型訓練方法。本研究試圖為解決云環境數據極度稀疏情況下的協同過濾算法計算效率及可擴展性提出新思路。

1 問題描述及方法分析

1.1 問題描述

推薦系統根據已有的用戶特征、行為(如查看、購買、評分)信息和商品特征信息，對已有商品進行評分預測，按預測的評分結果排序得到推薦列表，將相應的商品推薦給用戶。在推薦系統中，一般產生如下數據矩陣：用戶評分矩陣(User-Item評分矩陣)、用戶特征矩陣和商品特征矩陣。設User-Item評分矩陣R中包含m個用戶U={Ui|i=1,2,…,m}和n個商品I={Ij|j=1,2,…,n}，那么R可以用一個m×n矩陣表示，如式(1)所示

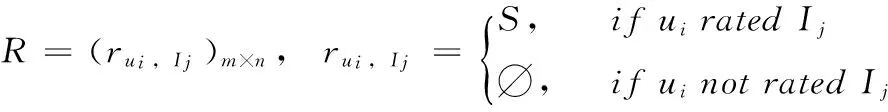
(1)

其中，評分r描述了用戶對不同商品的偏好程度，分數越高表示用戶越喜歡該商品；若r=?表示該用戶ui沒有對商品Ij評分，具體評分矩陣為R=[r1,1,…,r1,n;r2,1,…,r2,n;…;rm,1,…,rm,n]。

用戶特征表包含m個用戶和p個特征FU={FU,k|k=1,2,…,p}，如用戶的年齡、職業等。商品特征一般包含n個商品和q個特征FI={FI,l|l=1,2,…,q}，如商品的類型、品牌等特征。在協同過濾推薦時考慮用戶和商品的特征組合問題能取得更好的推薦質量。

1.2 現有方法及分析

協同過濾技術是根據用戶對商品或信息的行為偏好，發現用戶、商品或內容之間的相關性進行推薦，主要技術包括：基于用戶(user-CF)、基于商品(item-CF)和基于模型(model-CF)的協同過濾算法。主要技術的假設與定義見文獻[1]。

1.2.1 相似性度量方法

基于用戶或商品的協同過濾無需獲取用戶或商品特征，只依賴于現有評分數據和相似度計算方法對評分進行預測，所以User-Item評分矩陣越密集，預測精度越高。協同過濾中的相似度計算方法一般使用Jaccard相似系數、余弦相似度和Pearson相關系數。設用戶u和v之間的相似度為Sim(u,v)，3種相似度計算方式如式(2)、式(3)、式(4)所示[18]

(2)

(3)

(4)

User-CF或Item-CF方法的核心在于通過相似性計算找到用戶或商品的最近鄰居。但是，在評分矩陣極度稀疏的情況下，兩個用戶共有評分集合I(u,v)很小，通常只有幾個少數的商品。數據稀疏性使該方法無法得到準確的用戶或商品相似度，使得計算出的目標商品或用戶的最近鄰居不準確，導致算法精度不高。

1.2.2 基于模型的協同過濾

由于相似性度量方法的缺點，一些學者使用Model-CF進行研究。主要基于User-Item評分矩陣訓練出推薦模型，對未評分商品進行評分預測。其中協同過濾的經典算法Slo-peOne算法基于這樣一種假設：兩個商品的偏好值之間存在著某種線性關系，可以通過線性函數Y=mX+b來描述，即通過商品X的偏好值對Y的偏好值進行預測[9]。如式(5)所示

(5)

其中，I(u,v)為用戶u和v共同評分的項目集合，r代表用戶評分。

該算法簡單、快速、容易實現，但僅通過線性回歸計算商品間的評分差異對評分進行預測，沒有考慮商品間共同評分的用戶數目，導致算法精度不高。

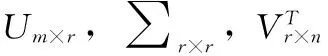
(6)

(7)

在云環境的大數據量情況下，該算法的r值選取存在一定的困難，選取過小會導致失去評分矩陣中的重要信息和結構；選取過大達不到降維的目的且容易導致訓練數據過擬合問題，嚴重影響算法精度。

上述傳統基于模型的協同過濾方法通過填充評分矩陣導致數據量急劇增長，且需要更多的迭代次數，使其計算效率和算法可擴展性不高，難以適應云環境下快速增長的數據量、數據高維化和算法可擴展性要求。

2 基于L-BFGS的協同過濾算法

2.1 基本思路

本算法屬于基于模型的協同過濾算法。算法改進思路為：使用L-BFGS優化算法對FM模型進行訓練，再使用FM模型進行評分預測，力求從精度和效率兩方面對協同過濾模型進行提升。在云環境下，User-Item評分數據維度越來越高的同時也變得越來越稀疏，使用FM模型對極度稀疏數據的良好學習能力，提高對用戶評分的預測精度。L-BFGS優化算法用來訓練FM模型在精度和效率上都有較好的表現。結合Spark分布式計算框架的特性，使本算法能夠適應云環境下的協同過濾推薦。

2.2 FM模型

本算法使用FM模型進行用戶對商品的評分預測以提高算法計算效率和精度。FM模型引進輔助向量對多項式模型(本文只考慮二階多項式模型)的二次項參數進行估計，旨在解決在數據稀疏情況下訓練多項式模型參數的問題[10]。

多項式模型的特征xi和xj組合一般用xixj表示，即xi和xj都不為零時，組合特征xixj才有意義。多項式模型二階方程為式(8)

(8)

其中，F代表樣本的特征數量，xi是第i個特征的值，w0、wi、wij是模型參數。每個二次項參數wij需要大量xi和xj都非零的樣本進行訓練，但實際推薦系統中數據稀疏度非常大，可供模型訓練的樣本極少，導致參數wij不準確進而嚴重影響模型的精度。

FM模型基于矩陣分解的思路，將式(8)中的二次項參數wij組成一個對稱矩陣W，使用矩陣分解方法可分解為W=VTV，V的第j列為第j維特征的隱向量，則二次項參數可以表示為wij=vi,vj。因此，FM模型方程如式(9)所示

(9)

其中，vi是第i維特征的隱向量，vi,vj代表向量點積，隱向量長度為K(K?F)。在式(9)中，二次項的參數數量為K×F個，相比多項式模型的二次項參數數量F(F+1)/2要大大減少。而由于將wij分解為兩個隱向量的點積vi,vj，所以特征組合xkxi和xixj的系數vk,vi和vi,vj有了共同項vi而不再相互獨立。即所有包含xi的非零特征組合的樣本都可以用來訓練vi，從而極大減輕數據稀疏性的影響。

對式(9)的二次項進行化簡，可將模型改寫為式(10)

(10)

化簡后的FM模型時間復雜度從O(KF2)優化到了O(KF)，極大提高模型計算效率。

使用FM模型進行預測時，考慮L2正則的優化目標函數，通常取式(11)

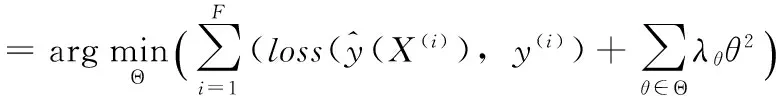
(11)

Rendle[10]使用了隨機梯度下降(SGD)、交替最小二乘法(ALS)和馬爾可夫鏈蒙特卡羅法(MCMC)3種學習算法來進行參數學習，也有較好的預測精度。但是在數據量劇增的情形下，上述算法需要的迭代次數和計算資源消耗較高，所以本文使用更適合實際業務的大規模優化算法：L-BFGS算法，來對FM模型進行參數訓練。

2.3 L-BFGS優化算法

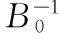
在L-BFGS算法中，迭代格式為式(12)

xk+1=xk+αkPk

(12)

式中，αk為步長，Pk為搜索方向，Pk的計算公式為式(13)

Pk=-Hk▽f(xk)

(13)

對L-BFGS算法過程，對sk和yk作如下定義

sk=xk+1-xk

(14)

yk=gk+1-gk

(15)

(16)

其中，gk≡▽f(xk)，上述式(14)和式(15)一維數組即是需要保存的每次迭代的曲率信息。

結合FM模型，L-BFGS算法流程如下：

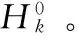
(17)

(18)

其中，τk為比例系數，E為單位矩陣。

步驟2 使用式(12)沿搜索方向找到下一個迭代點；

步驟3 根據Armijo-Goldstein準則和FM傳入參數允許偏差值ε判斷算法是否停止；

步驟4 如果|▽f(xk)|≥ε，使用式(13)更新搜索方向Pk；

步驟5 將訓練得到的參數w0、一次項參數矩陣W和二次項隱向量V返回到FM模型。

L-BFGS算法利用最近一次保存的曲率信息來估計實際Hassian矩陣的近似矩陣，這使得當前步的搜索方向較為理想，收斂速度較快，同時實際工程中，一般設置步長αk=1，在大多數情況下都是滿足的，節省了步長搜索時間，提高算法效率。

2.4 L-BFGS-CF算法流程

綜上，本文提出的L-BFGS-CF算法采用L-BFGS訓練FM模型參數，算法流程如圖1所示。L-BFGS-CF算法的詳細步驟如下：

輸入：數據集R，迭代次數T′，隱向量v維度，正則化系數λ，允許偏差ε

輸出：填充后的預測評分矩陣R′

步驟1 初始化Spark實例配置SparkContext()，讀取Spark環境配置；

步驟2 使用FM模型對數據集R進行格式化轉換并按8∶2比例隨機劃分為訓練集Rtrain和測試集Rtest；

步驟3 將轉換后的訓練集Rtrain、模型參數傳遞給L-BFGS算法；

步驟4 初始化L-BFGS參數，選擇初始點x0和需要存儲的迭代次數T′；

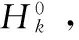
步驟6 根據式(12)進行迭代計算；

步驟7 如果|▽f(xk)|≥ε，根據式(13)計算搜索方向Pk，返回步驟6；

步驟8 如果|▽f(xk)|≤ε，返回訓練參數w0、W和V給FM模型；

步驟9 用式(10)對測試集Rtest商品進行評分預測，填充評分矩陣R′。

圖1 L-BFGS-CF算法流程

3 實驗設計及結果分析

3.1 實驗設計

為驗證L-BFGS-CF改進后的預測效果，采用4組不同數據量的數據集進行實驗。選取SVD++，KNN-100和基于聚類(記為Cluster)的3種協同過濾算法對比分析，驗證L-BFGS-CF的精度；其次增加實驗數據的特征個數，分析使用L-BFGS-CF算法數據特征數量與精度的關系；最后，使用不同迭代次數對L-BFGS-CF進行實驗，分析算法收斂速度。

3.1.1 實驗環境

實驗環境為VMware搭建的Spark高可用(HA)集群，包含3個節點：主節點為Master，子節點分別為Slave01和Slave02。安裝內存16 G，處理器為四核Intel Core i5 2.6.0 GHz，軟件環境為CentOS-6.7，Hadoop-2.5.0-cdh5.3.6，Spark-1.6.1-cdh5.3.6，Scala-2.10.4，jdk-1.7.67。內存及各組件分配見表1。

表1 實驗節點資源分配情況

3.1.2 實驗數據集

實驗數據集使用MovieLens(http://grouplens.org/datasets/movielens/)、NetFlix Prize(http://www.netflixprize.com/)及天池競賽(https://tianchi.shuju.aliyun.com/datalab/index.htm)數據集。MovieLens是由GroupLens Research從MovieLens站點提供的評分數據進行收集整理，此數據被廣泛用于研究協同過濾的實驗數據，分別選取數據量大小10萬和100萬的數據集：MovieLens-100K，MovieLens-1M。同時，為了驗證模型對不同數據集的適應性，采用天池競賽IJCAI-15 Dataset進行實驗。該數據集包含天貓40多萬用戶的5000萬條購買商品記錄，從中抽取1000萬條有效數據記為TMALL-10M，用于預測用戶再次購買同一商家商品的可能性。NetFlix數據集包含17萬多用戶的19億條評分記錄，由于實驗環境限制，本文從中選取1%的評分數據進行實驗，記為NetFlix-100M。

表2統計了各組數據集的特征數量情況，包括評分數量(rating)，用戶數量(user)，商品數量(item)，以及數據稀疏度(sparsity)，數據稀疏度通過式(19)計算。此外，用戶性別、用戶年齡及用戶職業等用戶特征，商品類型及標簽等商品特征可以直接從上述數據集中獲取

(19)

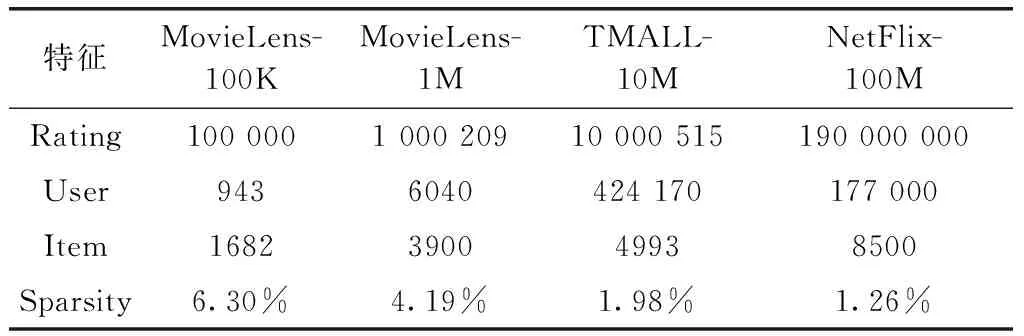
表2 實驗數據集特征

實驗從每個數據集中隨機選取80%作為訓練集，剩余20%作為測試集。通過劃分不同比例進行實驗，結果表明訓練集和測試集的比例劃分對L-BFGS-CF的影響甚微。

3.1.3 評判度量指標

推薦系統性能的評判度量指標通常使用均方根誤差(RMSE)和平均絕對誤差(MAE)。其中，RMSE作為NetFlix Prize賽事的標準度量指標；MAE廣泛使用于推薦系統預測精度的評判標準。RMSE和MAE越低，表示推薦系統的預測精度越高。各指標計算如式(20)和式(21)所示[1]

(20)

(21)

3.2 結果與分析

3.2.1 不同數據量下4種算法精度對比

為方便比較，選取迭代次數為100次和特征數量為4個的情況下進行實驗對比，結果如圖2和圖3所示。相比較小的數據集，NetFlix-100M的精度提升最為明顯。

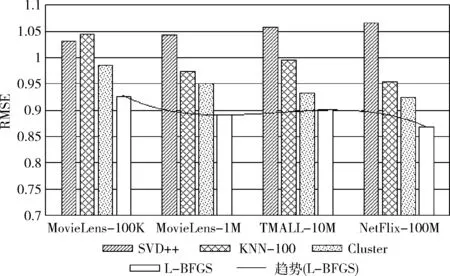
圖2 不同數據量大小情況4種算法的RMSE值對比

圖3 不同數據量大小情況4種算法的MAE值對比

(1)L-BFGS-CF與SVD++相比，RMSE和MAE值分別降低0.198和0.142。SVD++屬于矩陣分解的一種，由于是隨機填充User-Item評分矩陣，大量增加了數據量及算法復雜度，同時數據填充造成數據失真，從而使預測精度下降，這在數據量越大的時候變得更加明顯。

(2)與KNN-100相比，RMSE和MAE值分別降低0.085和0.063。KNN-100算法雖然無需訓練模型，但對于樣本不平衡的數據誤差比較大，且算法計算量大，在數據量很大時需要耗用大量的內存。

(3)與Cluster相比，RMSE和MAE值分別降低0.056和0.04。Cluster方法由于聚類中心往往是隨機選擇的，存在聚類結果不穩定的問題，同時算法復雜度高，在不斷地迭代過程中，保存的計算矩陣占用大量的內存和CPU時間，在精度和速率上都有所欠缺。

在不同大小的數據對比中，L-BFGS-CF算法均有最低的RMSE和MAE值，具有良好的預測精度。而對于TMALL-10M的數據集，由于預測結果為布爾類型，算法精度相比預測評分值的其它數據要低。

3.2.2 特征數量對L-BFGS-CF精度的影響

選取MovieLens-1M數據集考查L-BFGS-CF迭代次數T和特征數量F的關系，分析對算法精度的影響，結果如圖4和圖5所示。隨著L-BFGS-CF算法迭代次數的增加，3種特征數量的情況下算法MAE和RMSE值都逐漸減少；而隨著特征數量的增加，L-BFGS-CF算法的精度隨之提升，但需要更大的迭代次數才能達到較為理想的精度。

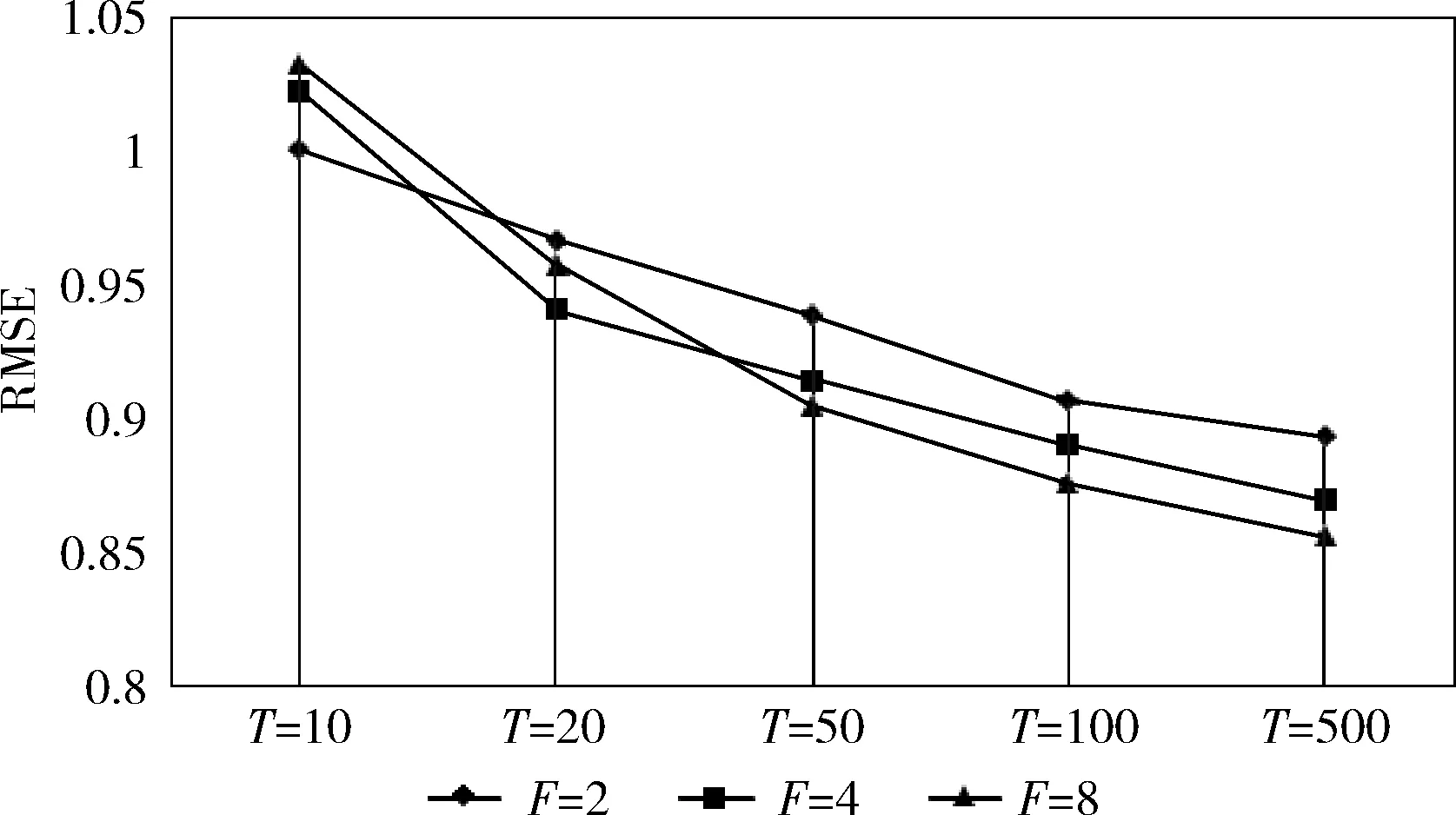
圖4 不同特征數量下L-BFGS-CF的RMSE值對比

圖5 不同特征數量下L-BFGS-CF的MAE值對比

3.2.3 L-BFGS-CF算法收斂速度分析

選取特征數量為4個的情況下使用不同迭代次數T考查算法收斂速度，結果如圖6和圖7所示。L-BFGS-CF算法的RMSE和MAE值隨著迭代次數的增加而逐漸變小，表明迭代次數是計算精度的主要影響因素之一。而不同大小的數據集來看，隨著數據集的增大，算法的RMSE和MAE值逐步減小；此外算法在迭代次數為10-50次的精度提升最為明顯。對于TMALL-10M數據，由于布爾類型的預測結果，在迭代次數50次左右達到相對穩定點。

圖6 不同迭代次數L-BFGS-CF的RMSE值對比

圖7 不同迭代次數L-BFGS-CF的MAE值對比

綜上可知，與其它3種協同過濾算法相比，L-BFGS-CF算法在規模不同的數據集均有最小的RMSE和MAE值，算法在迭代次數為50次可達到較好的精度，收斂速度快，且在適當增加迭代次數和數據集特征數量時能得到更好的預測精度。

4 結束語

本文針對所提出的基于L-BFGS優化的協同過濾算法的研究結論如下：

(1)算法設計上，采用FM模型對評分進行預測，FM模型使用輔助向量對的特征組合系數進行估計，避免了訓練數據的稀疏性對參數學習的影響；采用L-BFGS算法訓練模型具有收斂速度快和占用計算空間低等特點，在數據量劇增的云環境下具有良好的可擴展性。

(2)實驗結果表明：與SVD++、KNN-100和基于聚類的協同過濾算法相比，本算法的RMSE值分別降低了0.198，0.085，0.056；MAE值分別降低了0.142，0.063，0.04。在4種規模的數據集上都取得了最小的RMSE和MAE值，具有良好的推薦精度。同時在適當增加迭代次數和數據集特征可以取得更好的推薦質量。本文在Spark分布式計算框架實現本算法，有效提高了算法計算效率和保證推薦系統的實時性，更適合云環境下的個性化推薦問題。

未來的研究工作考慮將Fuzzy C-means聚類算法與本算法結合，在進一步節省計算資源消耗的同時提高算法推薦精度。

[1]Yang X,Guo Y,Liu Y,et al.A survey of collaborative filtering based social recommender systems[J].Computer Communications,2014,41(5):1-10.

[2]Hernando A,Bobadilla J,Ortega F.A non negative matrix factorization for collaborative filtering recommender systems based on a Bayesian probabilistic model[J].Knowledge-Based Systems,2016,97(C):188-202.

[3]WEI Suyun,XIAO Jingjing,YE Ning.Collaborative filtering algorithm based on Co-clustering smoothing[J].Journal of Computer Research and Development,2013,50(s2):163-169(in Chinese).[韋素云,肖靜靜,業寧.基于聯合聚類平滑的協同過濾算法[J].計算機研究與發展,2013,50(s2):163-169.]

[4]Cobos C,Rodriguez O,Rivera J,et al.A hybrid system of pedagogical pattern recommendations based on singular value decomposition and variable data attributes[J].Information Processing & Management,2013,49(3):607-625.

[5]Zhou X,He J,Huang G,et al.SVD-based incremental approaches for recommender systems[J].Journal of Computer and System Sciences,2015,81(4):717-733.

[6]NIU Changyong,LIU Guoshu.Collaborative filtering algorithm based on both local and global similarity and singular value decomposition(SVD)[J].Computer Engineering and Design,2016,37(9):2497-2501(in Chinese).[牛常勇,劉國樞.基于局部全局相似度的SVD的協同過濾算法[J].計算機工程與設計,2016,37(9):2497-2501.]

[7]Tsai CF,Hung C.Cluster ensembles in collaborative filtering recommendation[J].Applied Soft Computing,2012,12(4):1417-1425.

[8]CHEN Kehan,HAN Panpan,WU Jian.User clustering based social network recommendation[J].Chinese Journal of Computers,2013,36(2):349-359(in Chinese).[陳克寒,韓盼盼,吳健.基于用戶聚類的異構社交網絡推薦算法[J].計算機學報,2013,36(2):349-359.]

[9]DENG Xiaoyi,JIN Chun,HAN Qingping,et al.Improved collaborative filtering model based on context clustering and user ranking[J].Systems Engineering-Theory & Practice,2013,33(11):2945-2953(in Chinese).[鄧曉懿,金淳,韓慶平,等.基于情境聚類和用戶評級的協同過濾推薦模型[J].系統工程理論與實踐,2013,33(11):2945-2953.]

[10]Rendle S.Factorization machines with libfm[J].ACM Transactions on Intelligent Systems and Technology,2012,3(3):57.

[11]Baltrunas L,Ricci F.Experimental evaluation of context-depen-dent collaborative filtering using item splitting[J].User Modeling and User-Adapted Interaction,2014,24(1-2):7-34.

[12]Salah A,Rogovschi N,Nadif M.A dynamic collaborative filtering system via a weighted clustering approach[J].Neurocomputing,2016,175(A):206-215.

[13]Nilashi M,Jannach D,Bin Ibrahim O,et al.Clustering-and regression-based multi-criteria collaborative filtering with incremental updates[J].Information Sciences,2015,293(1):235-250.

[14]ZHANG Bangzuo,GUI Xin,HE Tang,et al.A novel reco-mmender algorithm on fusion heterogeneous information network and rating matrix[J].Journal of Computer Research and Development,2014,51(s2):69-75(in Chinese).[張邦佐,桂欣,何濤,等.一種融合異構信息網絡和評分矩陣的推薦新算法[J].計算機研究與發展,2014,51(s2):69-75.]

[15]Biglari F.Dynamic scaling on the limited memory BFGS met-hod[J].European Journal of Operational Research,2015,243(3):697-702.

[16]LI Weitao,ZHOU Yuanfeng,GAO Shanshan,et al.Rapid sampling on implicit surfaces via hybrid optimization[J].Chinese Journal of Computers,2014,37(3):593-601(in Chinese).[李偉濤,周元峰,高珊珊,等.基于混合優化的快速隱式曲面采樣方法[J].計算機學報,2014,37(3):593-601.]

[17]Biglari F,Ebadian A.Limited memory BFGS method based on a high-order tensor model[J].Computational Optimization and Applications,2015,60(2):413-422.

[18]Liu H,Hu Z,Mian A,et al.A new user similarity model to improve the accuracy of collaborative filtering[J].Know-ledge-Based Systems,2014,56(3):156-166.