微分遞推法在艦船靜態電場深度換算中的應用研究

孫嘉慶, 陳聰, 危玉倩, 李定國

(海軍工程大學 基礎部, 湖北 武漢 330031)

0 引言

遞推算法是指在一定的遞推模型基礎上，利用體系內部各分體系之間的分布、邊界、數量等相關規律，建立遞推關系，再依據遞推關系逐步遞推求解的方法[1-3]。微分法則是通過對整體進行合理劃分，利用微分學公式來對復雜問題進行求解的方法[4]。在工程計算中，對于受多種交叉因素所影響的復雜體系而言，由于傳統的解析法一般都是從體系的整體性質或邊界條件出發，受交叉因素的復雜性影響，直接采取解析法來對體系進行分析往往比較困難。相比之下，利用遞推算法與微分法相結合的微分遞推法，先對體系進行合理劃分，再從體系內部各分體系之間的遞推關系出發，往往能夠大大簡化分析計算過程。

船舶靜態電場是重要的水下軍用目標特性，由于測試條件的限制，實際應用中往往需要進行電場分布的深度換算[5-6]。而由于場域邊界的存在及船舶附近海水區域中腐蝕電流和防腐電流的復雜性，使得船舶靜態電場的深度換算成為一個難題。文獻[7]將艦船靜態電場的場源等效為一組電性模擬體，借助測量平面上電場強度三分量的數據和分布特征反演出場源的參數，再通過這些參數求解出其他深度平面上的電場強度三分量的分布。盡管從理論上講，這一方法適用于各類深度換算問題，但若希望對模擬源的所有參數進行準確反演，則對算法的要求非常高，實際應用中很難實現。文獻[8]從艦船靜態電場的物理特性出發,提出基于拉普拉斯方程的靜態電場深度換算方法，實現了由靜態電場的某分量向較大深度該分量的自換算，由靜態電場的垂直分量向較大深度其他分量的互換算以及由靜態電場的水下標量電位實現向較大深度的電場各分量換算。這種方法在一定程度上降低了計算量，但由于拉普拉斯方程對邊界條件的要求，這一方法無法實現在淺海區域內的深度換算。

徐世浙[9]給出了解決地磁勘探領域位場延拓的積分迭代法,受此啟發，閆輝等[10]、胡英娣等[11]提出利用微分遞推法解決電場和磁場深度換算問題的方法，并對換算結果進行仿真分析，說明了微分遞推換算法的可行性，但卻只給出單一方向換算問題的換算結果，沒有進行進一步誤差分析。

本文針對微分遞推換算法在艦船靜態電場深度換算問題中應用的方法及誤差來源開展研究。由水平測量平面上網格節點處電場強度三分量的測量值獲得其水平偏導數，再利用換算區域內靜態電場的無源、無旋特性，得到電場強度三分量豎直方向上的1階偏導數。通過對換算區域的離散化處理，在兩相鄰深度平面之間建立以牛頓- 萊布尼茨公式為基礎的遞推關系，通過逐層遞推，實現場分量的深度換算。同時以艦船電場的基本模擬單元——水平電偶極子產生的電場為對象，對由近及遠和由遠及近兩類換算問題進行仿真分析，論證微分遞推換算法在一定換算深度范圍內的可行性，并對測量平面的節點間隔、遞推步長、海水深度等因素對換算誤差的影響進行研究，給出換算誤差隨上述因素的變化規律。

1 微分遞推換算法

1.1 微分遞推原理

船舶靜態電場的深度換算問題分為兩類：一類是由近源平面向遠源平面的換算問題，即在靠近源(船)的平面上對場進行測量，由此換算至離源較遠的目標平面上，稱為由近及遠換算，如圖1所示；另一類是由離源較遠的測量平面向離源較近的目標平面的換算問題，稱為由遠及近換算，如圖2所示。在測量平面與目標平面之間以Δz為間隔插入N-1個等間距的平面，如圖1、圖2所示。根據遞推法的基本思路，只要得到兩相鄰中間層平面上電場強度三分量之間的數值關系，就可以通過循環遞推N次，得到目標平面上的電場強度三分量的數值。

根據牛頓- 萊布尼茨公式，位于兩相鄰中間層z=zk與z=zk+1上具有相同x坐標、y坐標的任意兩點的電場強度三分量存在以下關系：

(1)

若Δz足夠小，則得到兩相鄰中間層的遞推關系式為

(2)

1.2 垂向偏導數的獲得

根據艦船水下靜態電場的產生機理可知，在測量平面與目標平面之間的換算區域內，該場具有無源、無旋的特性，也就是有

(3)

將(3)式進行3個方向上的分解，即

(4)

式中：i、j、k分別為x軸方向、y軸方向、z軸方向的單位矢量。

即有

(5)

結合(2)式、(5)式，遞推關系式可改寫為

(6)

實際應用中，若獲得一個水平面上網格節點處的場分布，則易于求出各節點處場分量的水平偏導數，本文采用1階導數計算方法。

1.3 水平方向偏導數的計算

若函數f(x)定義在[a,b]上，x0、x1、x2、x3、x4為間距均為h的等距節點，且a≤x0≤x1≤x2≤x3≤x4≤b.f(xk)為節點處的函數值，其中k=0,1,2,3,4. 則節點處f(x)的1階導數[12]為

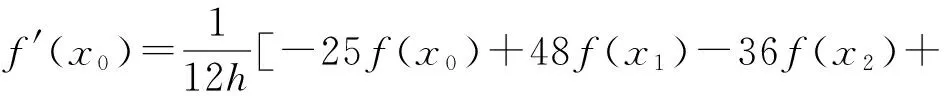
(7)

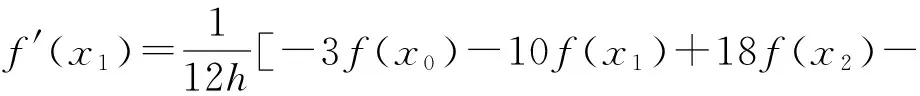
(8)

(9)

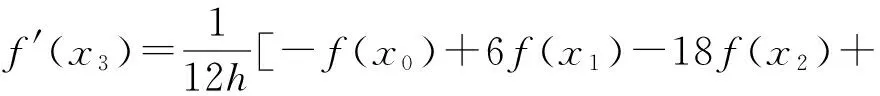
(10)

(11)

式中：ξi∈(a,b)，i=0,1,2,3,4.

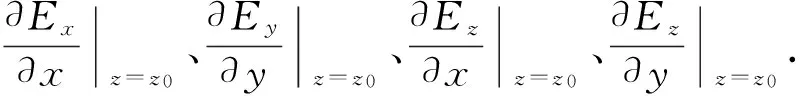
2 微分遞推換算法的算法設計

由上文所述思路，遞推算法在艦船靜態電場的深度換算中應用時包括以下步驟：

1)由網格狀測量平面上節點處的電場強度三分量測量值，利用(7)式～(11)式求出其1階水平偏導數。

2)根據(5)式，由水平偏導數求出各節點處電場強度三分量的垂向偏導數。

3)由(2)式求出下一相鄰平面上或上一相鄰平面上電場強度三分量的值。

4)重復步驟1～步驟3，最終得到目標平面上場。

具體算法設計框圖如圖3所示。圖3中：下標x、y、z代表電場強度在某方向的分量；下標i、j表示節點的位置編號，即x軸方向第i個、y軸方向第j個網格節點；下標k為遞推步數，也表示第k層遞推平面，k=0為測量平面。

3 微分遞推換算法的可行性驗證

3.1 兩類換算問題的仿真換算結果

設海水電導率為4 S/m，海床電導率為0.4 S/m. 空氣- 海水界面取為z=0的平面，豎直向下為z軸正方向，以水平電偶極子電偶極矩方向為x軸正方向。將微分遞推換算法應用于由遠及近和由近及遠兩類深度換算問題，換算涉及到的相關參數設置如表1所示。

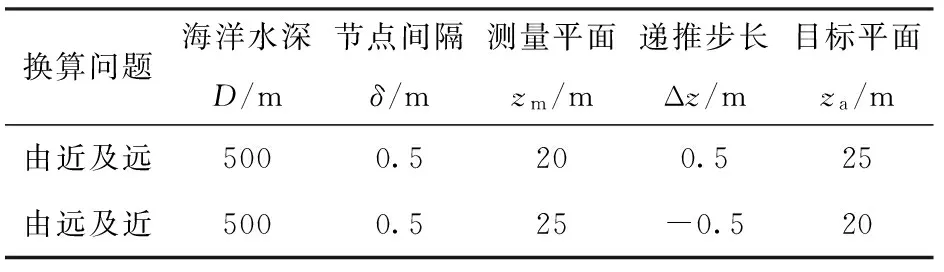
表1 仿真參數

換算結果如圖4、圖5所示。

為了更全面準確地表征換算結果的精度，本文采用目標平面的換算值與該平面的理論計算值之間的相對均方根誤差RRMSE、最大值相對誤差ep、最小值相對誤差eb來描述換算誤差。以Ex為例，如(12)式～(14)式所示。

(12)

(13)

(14)

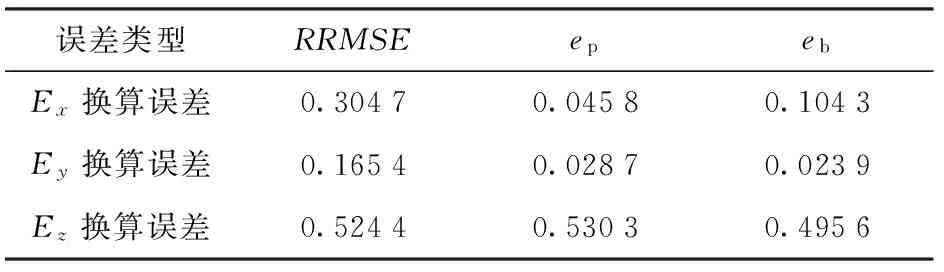
式中：下標c、t分別表示換算值與理論計算值。另外本文所取RRMSE為換算值的均方根誤差RMSE與計算值的均方根平均值RMSA的比值。圖4、圖5對應的換算誤差分別如表2、表3所示。

顯然，從表2、表3可以看出，無論是由近及遠還是由遠及近換算，其電場強度三分量換算誤差的最大值均不超過0.035，換算精度較高。

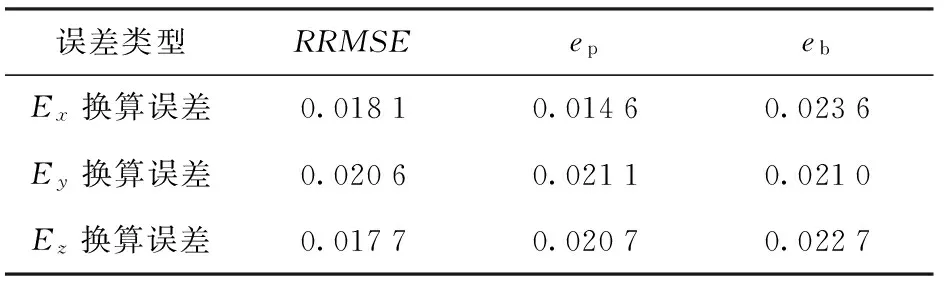
表2 由近及遠換算誤差

表3 由遠及近換算誤差

保持其他參數條件不變，只改變目標平面深度，使換算深度H分別為1 m、2 m、3 m、4 m、5 m、6 m、7 m、8 m、9 m、10 m、11 m，分別計算由近及遠和由遠及近兩類換算問題的相對均方根誤差，如圖6、圖7所示。

由圖6、圖7可知，隨著換算深度的增大，換算精度不斷下降。其中：由圖6可知，在本文所選換算參數條件下，當H>7 m時，由近及遠的換算誤差迅速增大，最終H=11 m時電場強度三分量的換算誤差均超過了50%；相比之下，由遠及近的換算中，換算誤差隨換算深度的變化比較平緩，如圖7所示，且可以計算，當換算深度H=20 m時，換算誤差才達到50%.

上述仿真結果表明，微分遞推換算法對于由遠及近和由近及遠兩類換算問題均適用，并且相較于由近及遠的換算問題來說，在解決由遠及近換算問題時，該方法能保持較好的換算精度。出現這個現象的原因在于5點微分公式應用于求電場強度三分量的水平偏導數時，其誤差隨深度不斷減小。采用對水下電場場強表達式直接求導和先求場再利用5點微分公式求導這兩種方法，編程數值計算某深度平面上電場強度三分量水平偏導數的值。將它們進行比較可以發現，對于遠源平面，5點微分公式求導所帶來的誤差較近源平面要小。這就導致由遠及近換算的起始過程誤差較小，反復迭代過程中誤差逐步增大；而由近及遠換算的起始過程誤差就較大，反復迭代使得誤差增大更快，最終導致兩平面之間的深度換算中，由遠及近的換算誤差更小。

實際工程應用中，廣泛采用的海床基測量點陣往往能夠提供海床- 海水界面上的場分布，此時一般需要進行由遠及近的換算，顯然前述研究結果表明，微分遞推換算法應為利用海水- 海床界面上的場分布進行由遠及近換算的適用方法之一。

3.2 實測場分布的換算結果

在實驗室中模擬空氣- 海水- 海床3層海洋環境，模擬海水水深0.53 m，電導率為0.204 7 S/m. 采用通有穩恒電流的兩平行鉑片模擬靜態電偶極子，兩鉑片間距0.03 m，外加電流0.2 A，置于水面下0.03 m深度處，坐標系建立同3.1節。 選取電偶極子下方、以電偶極子投影點為中心、大小為0.25 m×0.25 m、深度分別為0.20 m和0.26 m的兩個平面進行電場強度的測量。結果如圖8、圖9所示。

以水深0.26 m處平面為測量平面，以水深0.20 m處平面為目標平面，采用前文所述的微分遞推換算法進行深度換算，電場強度三分量換算結果如圖10所示。

對比圖10與圖9可以看出，換算所得目標平面上的電場強度三分量的場分布特征與實測結果吻合較好。為了更精細地表達換算精度，表4也給出了換算值與實測值之間的RRMSE、ep和eb. 考慮到實際測量誤差條件和電場強度測試系統本身的測試精度的影響，表4所示的誤差表明微分遞推換算法應用于艦船靜態電場深度換算是可行的。

4 微分遞推換算法換算精度的仿真分析

在3.1節中設置的仿真參數基礎上，保持測量平面大小，通過改變其他相關參數，采用仿真分析的方法分別研究遞推步長、測量平面網格節點間隔以及海水深度對換算精度的影響。

4.1 遞推步長對換算精度的影響

選取深度為20 m和26 m的兩個平面分別進行由近及遠和由遠及近換算。選取測量平面網格節點間隔δ=0.1 m，海水深度D=100 m. 分別計算遞推步長的絕對值為0.10 m、0.15 m、0.20 m、0.25 m、0.30 m、0.40 m、0.50 m、0.60 m、1.00 m、2.00 m時電場強度三分量的RRMSE，如圖11、圖12所示。

由圖11、圖12可知：在由近及遠換算中，隨著遞推步長的增大，電場強度三分量換算的RRMSE均呈現出先減小、后增大的趨勢；而在由遠及近換算中，電場強度三分量換算的RRMSE則呈現單調增大的趨勢。

誤差類型RRMSEepebEx換算誤差0.30470.04580.1043Ey換算誤差0.16540.02870.0239Ez換算誤差0.52440.53030.4956

從微分遞推換算法原理上來看，遞推步長主要通過兩種效果相反的效應來影響換算精度。一方面是近似效應，即在(1)式近似為(2)式的過程中，若Δz并非足夠小，則會引入換算誤差，且Δz越小，因近似引入的誤差就越小；另一方面是遞推過程中的誤差累積效應，Δz越小，換算次數越多，誤差因累積也就越大。對比圖11、圖12可知：對于由遠及近換算而言，在圖示的遞推步長范圍內，近似效應始終占據主導；而對于由近及遠換算而言，誤差累積和近似效應先后占據主導地位，使得誤差出現先減小、后增大的趨勢。因此，在選擇合適的遞推步長時，對于由遠及近換算問題，應當在不影響運算效率的前提下，盡可能選擇小的遞推步長；而對于由近及遠換算問題，則應當選擇靠近極值點處的遞推步長。

4.2 測量平面網格節點間隔對換算精度的影響

選取深度為20 m和30 m的兩個平面分別進行由近及遠和由遠及近換算。選取遞推步長Δz=0.1 m，海水深度D=100 m. 應用微分遞推換算法，分別計算測量平面網格節點間隔δ為0.1 m、0.2 m、0.3 m、0.4 m、0.5 m、0.6 m時的電場強度三分量的RRMSE，如圖13、圖14所示。

由圖13、圖14可知，盡管隨著網格節點間隔的增大，電場強度三分量的換算誤差呈現增大趨勢，但增大不明顯。由遠及近換算中，網格節點間隔從0.1 m變化到0.6 m，換算的RRMSE變化不超過0.005；而在由近及遠換算中，RRMSE變化不超過0.05.

從微分遞推換算原理來看，網格節點間隔影響1階偏導數計算公式中的差值余項，但顯然影響并不大。但在編程應用微分遞推換算法進行換算過程中，網格節點間隔對于運算量及運算效率的影響非常大，因此在實際應用中，為了保證運算速度，網格節點間隔可以設置的稍大一點。這一點對實際的測量工作也非常有益，網格節點間隔大，減少了傳感器的需求數量，也降低了布設難度。

4.3 海洋水深對換算精度的影響

選取深度為20 m和25 m的兩個平面分別進行由近及遠和由遠及近換算。選取測量平面網格節點間隔δ=0.1 m，遞推步長Δz=0.1 m，應用微分逆推換算法，分別計算海水深度D為30 m、40 m、50 m、60 m、70 m、80 m、90 m、100 m時電場強度三分量的RRMSE，如圖15、圖16所示。

由圖15、圖16可知，在本文設定的參數條件下，海水深度小于50 m時，海床的存在會影響換算精度；而海水深度大于50 m后，電場強度三分量換算誤差逐漸穩定在一個較低的水平上，也就是說海床的影響可以不考慮。

海水深度對微分遞推換算法換算精度的影響主要表現在海水深度越大，換算區域邊界距離海床越遠，海床對換算的影響也就越小，因此，在實際應用中，微分遞推換算法在解決貼近海床區域的深度換算問題時應當慎重。前文已經提到在實際應用過程中，經常遇到以海水- 海床界面為測量平面進行由遠及近換算的問題。下面考察利用海床基測量值進行由遠及近換算時，換算誤差隨換算深度的變化。保持其他參數條件不變，設海洋水深D=40 m，測量平面為海水- 海床界面即zm=40 m，分別計算換算深度H為5.0 m、7.5 m、10.0 m、12.5 m、15.0 m、17.5 m、20.5 m時，由遠及近換算的RRMSE，如表5所示。

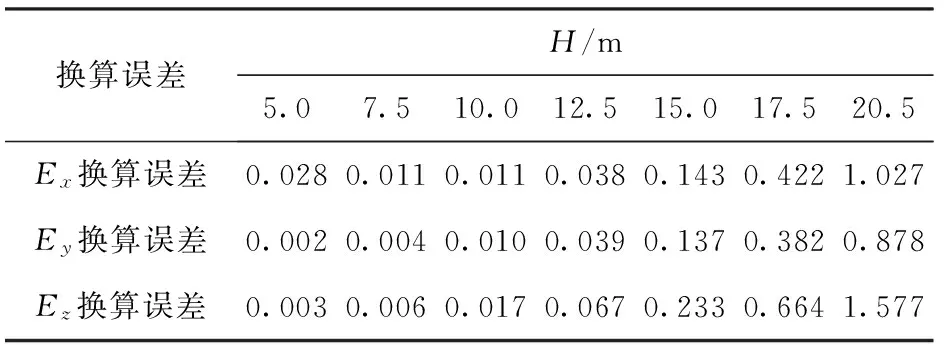
表5 以海水- 海床界面為測量平面時換算誤差隨換算深度的變化

由表5可知，以海水- 海床界面為測量平面進行由遠及近換算時，隨著換算深度的增大，換算誤差不斷增大，但在本文所設參數條件下，換算深度在5.0～15.0 m范圍內時，電場強度三分量的換算RRMSE均不超過25%，換算精度較高。這表明在實際應用過程中，以海水- 海床界面為測量平面布設測量基陣時，在一定的換算深度范圍內，利用微分遞推換算法進行由遠及近換算，可得到較為可靠的目標平面電場分布。

5 結論

本文對測量平面與目標平面之間所構成的換算區域進行離散化處理，利用牛頓- 萊布尼茨公式建立起兩中間平面之間的遞推關系，依據換算區域內場的無源、無旋特性將電場強度三分量垂向偏導數的求解問題轉化成了水平偏導數的計算問題，給出了微分遞推換算法用于艦船靜態電場深度換算的方法并設計了算法。本文還通過仿真模擬與實驗驗證，說明了在一定換算深度范圍內應用微分遞推換算法進行換算的可行性。隨后采用仿真分析方法，分別考察了遞推步長、測量平面網格節點間隔和海洋水深對微分遞推法換算精度的影響，得到以下結論：

1)遞推步長的增大會帶來兩種效果相反的效應，一方面會導致離散化處理的近似效果下降，增大誤差；另一方面由于遞推次數的減少會導致誤差累積效應的下降，誤差也減少。對由近及遠換算，存在一個最佳的遞推步長，而對由遠及近換算，則應當在不影響運算效率的前提下，盡可能選擇小的遞推步長。

2)網格節點間隔變化引起的誤差變化很小，這是由于本文所采取的1階導數計算方法對節點間隔不敏感。因此實際應用中，為提高換算速度、減少測量基陣布設難度，可以選擇較大的網格節點間隔。

3)海水深度對于遞推算法的影響主要取決于換算區域與海床的距離。如果換算區域離海床較遠，則受海床的影響較小，換算誤差也可以穩定在一個較小的水平。

4)在同等參數條件下，采用微分遞推法進行由遠及近換算的精度要優于由近及遠換算的精度。而實際軍事應用中，以海水- 海床界面為測量平面進行由遠及近換算需求較多。仿真結果表明，盡管隨著換算深度的增大，其換算精度有所下降，但在一定范圍內，其換算精度還能保持在一個較高的水平上。另外從本文研究也可看出，微分遞推法應用于艦船水下靜態電場深度換算時，算法過程簡潔、測量基陣布設難度不大，因此該方法具有明顯的軍事應用前景。

)

[1] Portnoy I, Melendez K, Pinzon H, et al. An improved weighted recursive PCA algorithm for adaptive fault detection[J]. Control Engineering Practice, 2016, 50:69-83.

[2] Dun X D, Jin W Q, Lu L. Noise-robust boundary recursive algorithm for super-resolution reconstruction of staring focal plane array micro-scanning imaging[J]. Infrared Physics & Technology, 2015, 68(11):159-166.

[4] Fernandes J F P, Camilo F M, Machado V M. Fluxball magnetic field analysis using a hybrid analytical/FEM/BEM with equivalent currents[J]. Journal of Magnetism & Magnetic Materials, 2016, 401:1173-1180.

[5] 王瑾. 艦船水下電場測量[J]. 中國艦船研究, 2007, 2(5):45-49.

WANG Jin. Measurement of underwater electric field for ships[J]. Chinese Journal of Ship Research, 2007, 2(5): 45-49.(in Chinese)

[6] Certenais J, Periou J J. Electromagnetic measurements at sea[C]∥Conference Proceedings of UDT.Germany：UDT，1997: 433-434.

[7] 陳聰, 李定國, 龔沈光. 船舶靜態電場深度換算方法[J]. 哈爾濱工程大學學報, 2009, 30(6): 719-722.

CHEN Cong, LI Ding-guo, GONG Shen-guang. The method of the extrapolation of the static electric field of ships[J]. Journal of Harbin Engineering University, 2009, 30(6): 719-722.(in Chinese)

[8] 陳聰, 李定國，龔沈光. 基于拉氏方程的艦船靜態電場深度換算[J]. 電子學報, 2010, 38(9):2025-2029．

CHEN Cong, LI Ding-guo, GONG Shen-guang. Research on the extrapolation of the static electric field of ships based on Laplace equation[J]. Acta Electronica Sinica, 2010, 38(9): 2025-2029.(in Chinese)

[9] 徐世浙. 位場延拓的積分- 迭代法[J]. 地球物理學報, 2009, 49(4): 1176-1182.

XU Shi-zhe. The integral-iteration method for continuation of potential fields[J]. Chinese Journal of Geophysics, 2006, 49(4): 1176-1182.(in Chinese)

[10] 閆輝, 肖昌漢, 殷克全, 等.遞推算法在船舶磁場遠場向近場換算中的應用[J]. 兵工學報, 2010, 31(9):1200-1203.

YAN Hui, XIAO Chang-han, YIN Ke-quan,et al. The application of recursive algorithm on ship’s magnetic field extrapolation[J].Acta Armamentarii, 2010, 31(9): 1200-1203.(in Chinese)

[11] 胡英娣, 龔沈光, 閆永貴. 一種新的船舶靜態電場深度換算方法[J]. 海軍工程大學學報, 2013, 25(5):16-20．

HU Ying-di, GONG Shen-guang, YAN Yong-gui. A new method for depth extropolation of ship’s electric field[J]. Journal of Naval University of Engineering, 2013, 25(5): 16-20.(in Chinese)

[12] 王燕. 一階導數的五點數值微分公式及外推算法[J]. 數學的實踐與認識, 2011, 41(6): 163-167．

WANG Yan. The extrapolation method of five-point numerical formulas for one-order derivative[J]. Mathematics in Practice and Theory, 2011, 41(6): 163-167.(in Chinese)

[13] 劉勝道. 艦船水下電場的測試技術與電偶極子模型研究[D]. 武漢: 海軍工程大學, 2002: 48- 65.

LIU Sheng-dao. The technology for measuring the underwater electric field and the electric dipole modeling research of ships[D]. Wuhan: Navy University of Engineering, 2002:48-65. (in Chinese)

[14] 陳聰, 龔沈光, 李定國. 基于混合模型的艦船腐蝕相關靜態電、磁場[J]. 哈爾濱工業大學學報, 2010, 42(3):495-499.

CHEN Cong, GONG Shen-guang, LI Ding-guo. Corrosion related static electric and magnetic field of ships based on mixed modeling[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 495-499.(in Chinese)

[15] 陳聰, 李定國, 龔沈光. 淺海中靜態電偶極子電場分布的鏡像法研究[J]. 武漢理工大學學報：交通科學與工程版, 2010, 34(4):716-720.

CHEN Cong, LI Ding-guo, GONG Shen-guang. Research on the electric field produced by static electric dipole located in shallow sea with mirror image theory[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2010, 34(4):716-720.(in Chinese)

[16] Hoitham P，Jeffery I，Brooking B，et al．Electromagnetic signature modeling and reduction[C]∥Conference Proceedings of UDT. London, UK: UDT，1999：97-100．