基于改進的PSO-SVM項目安全預測模型仿真與驗證

李書全，劉世杰

（天津財經大學管理科學與工程學院，天津300222）

0 引言

近年來，基于粒子群算法優化的支持向量機（PSOSVM）在預測模型中得到了廣泛應用[1，2]，該模型預測誤差小，精度高，具有較快的收斂速度，實現方便，適用于小樣本和非線性的預測問題。建筑施工活動具有復雜性、分散性和人員流動性的特點，因此該模型比較適用于建筑施工項目的安全預測，能夠取得較好的效果。傳統的PSO-SVM模型在對SVM參數尋優過程中容易陷入局部最優，進而影響預測的精度[3]。鑒于此，本文以施工企業項目部為研究對象，并引入社會資本作為重要影響因素，利用粗糙集屬性約簡的方法辨識影響施工項目安全的要素，在此基礎上將改進的粒子群算法與支持向量機相結合，建立了基于改進PSO-SVM的安全預測模型。并進行了仿真模擬，驗證了該模型的有效性和實用性，為施工項目的安全預測提供科學的理論依據。

1 模型算法優化

支持向量機（SVM）是Vapnik于1995年提出來的一種計算機模型，可有效解決復雜的非線性回歸問題，其基本思想是運用非線性映射將數據映射到高維特征空間里，然后在此高維特征空間對其進行線性回歸[2]。粒子群（PSO）算法由Eberhart和Kenney于1995年提出的一種基于群體智能的優化算法，它是模擬鳥群隨機搜尋食物的捕食行為，并從這種行為中得到啟示并用于解決優化問題[1]。SVM的懲罰參數和核函數參數的選擇是非常重要的問題，直接影響SVM的精度。使用傳統的網格搜索方法選取SVM參數，該方法精度低且花費時間較長。將PSO應用于SVM的參數優化問題，可以得到SVM的最佳懲罰參數和核函數參數，進而可以提高施工項目安全預測模型的訓練速度和準確度。但是傳統PSO算法存在全局尋優能力較差，容易發生早熟收斂的問題[4]。為了解決這些問題，本文結合了慣性權重的自適應調整[5]和高斯擾動[4]的思想，對PSO算法進行了改進，在此基礎上利用改進的粒子群算法（PSO）優化支持向量機（SVM）的參數，構建項目安全預測模型。改進后的PSO-SVM模型有效解決了粒子群陷入局部最優點的問題，預測精度更高，誤差更小，可用于建筑施工項目安全預測模型的構建。

1.1 慣性權重的自適應調整

首先定義標準適應度（Normalized Fitness Value，NFV）的概念[5]來引導粒子更快地收斂到全局最優粒子位置。

式（1）中，fgbest為種群全局最優適應度；fmax為粒子個體的歷史最大適應度；fmin為粒子個體的歷史最小適應度。在此基礎上，將慣性權重w定義為：

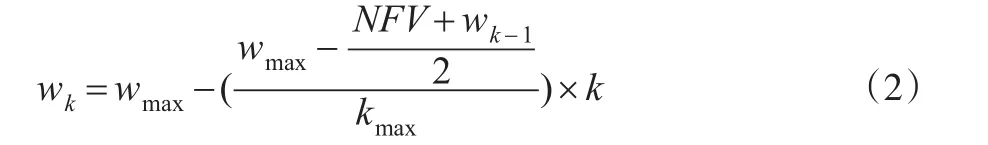
式（2）中，wk為第k次迭代中的w值，wk-1為第k-1次迭代中的w值，wmax為w的最大值，kmax為最大迭代次數。由式（2）可知，如果在第k次迭代中的NFV優于上一次迭代的值，表明該粒子所在區域存在優于全局最優值的概率較大，因此減小w的值以提高算法的局部尋優能力；反之，為了跳出當前區域，增加w的值以提高算法的全局搜索能力。這種根據適應度值調整慣性權重的方法，避免了粒子陷入局部極值點，提高了收斂速度。

1.2 高斯擾動的PSO算法

在標準PSO算法中，粒子根據如下公式來更新自己的速度和位置。

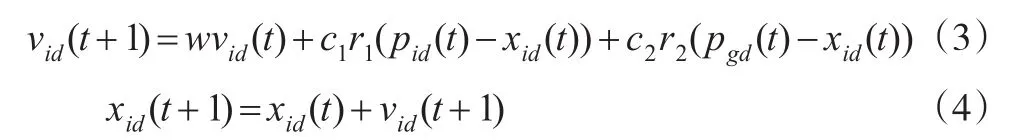
式（3）中，xid(t)為第t次迭代中粒子的位置；νid(t)為第t次迭代中粒子的速度；pid(t)和pgd(t)為第t次迭代中的粒子個體最優位置和種群全局最優位置；w為慣性權重；c1和c2為學習因子；r1和r2為[0,1]范圍內均勻分布的隨機數。采用高斯擾動策略，在公式（3）中，用全部粒子的含有高斯擾動項的個體最優位置總和的平均值代替pid(t)[4]。改進后的粒子速度更新公式如下所示：

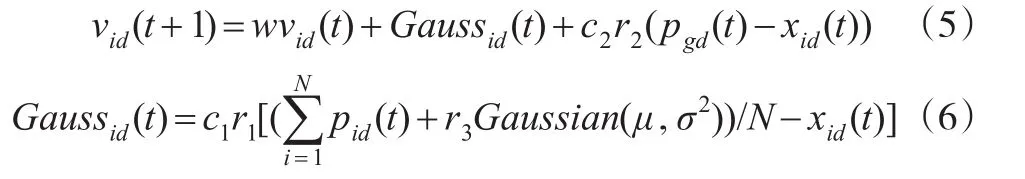
式（5）中Gaussid(t)為在第t次迭代中的高斯擾動項，式（6）中Gaussian(μ,σ2)為服從高斯分布N(μ,σ2)的隨機數，N為種群規模大小，r3為[0,1]范圍內均勻分布的隨機數。這種方法可有效增強粒子的逃逸能力，有利于粒子之間最優位置信息的共享，進而提高算法收斂精度。

2 模型仿真模擬

為了驗證模型的可行性，本文參考已有研究成果的問卷調查數據，從中選取87個有效樣本進行模型的仿真模擬。選取前60組樣本數據作為模型的訓練數據，將該60組數據中影響施工項目安全績效的關鍵因素作為自變量，將項目安全績效評價值作為因變量。然后選取另外27組樣本數據作為測試數據，并使用mapminmax函數分別對訓練數據及測試數據進行歸一化處理。

2.1 PSO參數尋優流程

利用PSO參數尋優的流程如下：

（1）設置PSO的參數，包括種群數量sizepop、最大迭代次數maxgen、局部搜索能力參數c1、全局搜索能力參數c2、慣性權重w。

（2）產生初始粒子的位置x(i)和速度v(i)。

（3）計算初始粒子的適應度fitness(i)，適應度取值為對訓練集進行交叉檢驗時的平均均方誤差（Mean Squared Error，MSE）。

（4）根據初始粒子適應度確定個體極值local_x和群體極值global_x。

（7）根據公式νid(t+1)=wνid(t)+Gaussid(t)+c2r2(pgd(t)-xid(t))更新粒子速度，根據公式xid(t+1)=xid(t)+νid(t+1)更新粒子位置。

（8）計算粒子的適應度值。

（9）將粒子的當前適應度值和個體極值比較，更新個體極值；將粒子的個體最優值和群體極值比較，更新群體極值。

(10)判斷是否達到算法終止條件，即是否達到最大進化代數或小于給定精度。如果滿足終止條件，算法停止運行并輸出最優粒子的位置參數，即SVM的最優懲罰系數c和核函數參數g，否則轉到（5）繼續運行。

在算法進行初始化時，設定種群數量為20，迭代次數為100次，c1=1.5，c2=1.7，w=1。核函數參數c設定的范圍為[0.1,100]，參數g設定的范圍為[0.01,1000][6]。PSO參數尋優的過程如圖1所示。

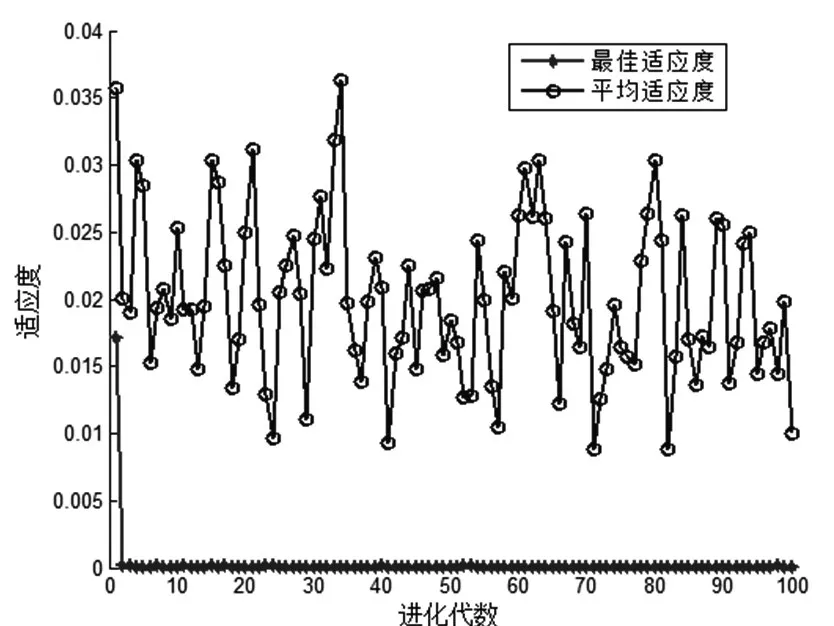
圖1 PSO尋找最佳參數的適應度曲線

從圖1中可看出，參數尋優后得到的最佳參數c=18.5079，最佳參數g=0.01，最佳平均MSE=0.00041968。

2.2 回歸擬合分析

本文使用MATLAB2012b和LIBSVM工具箱實現SVM模型。SVM核函數選擇徑向基核函數（RBF），因為無論是小樣本還是大樣本，高維還是低維等情況，RBF核函數均適用。在確定核函數和參數c、g后，利用LIBSVM的訓練命令svmtrain對60組樣本數據進行訓練，得到訓練模型。然后利用預測命令svmpredict對27個樣本的測試數據進行回歸預測，模型原始數據和回歸預測數據對比圖、誤差圖如圖2所示。

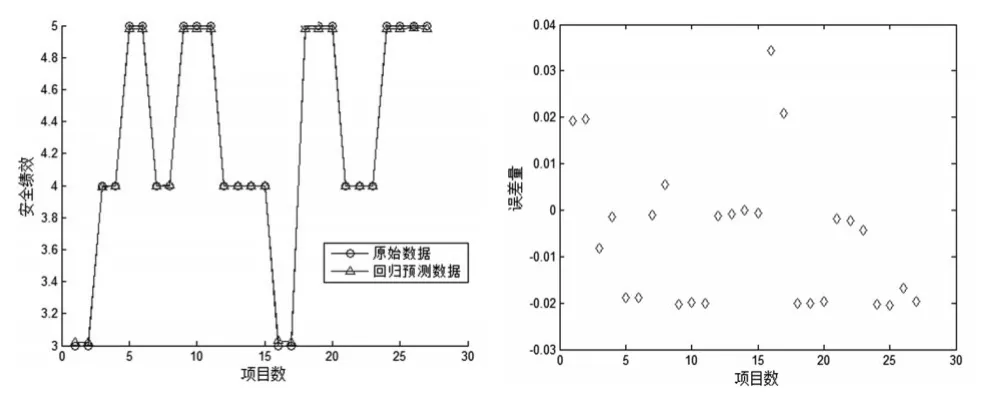
圖2 改進的PSO-SVM模型仿真模擬結果

結果顯示該模型預測的MSE=0.000659123，擬合相關系數=99.2974%，,絕對誤差值分布在-0.03到0.04之間。結果表明本模型具有較高的預測精度，可用于施工項目安全預測建模。

3 模型驗證分析

3.1 數據來源及處理

社會資本理論認為，組織或個體之間存在的信任、溝通、非正式規范等對企業績效有積極的影響[7]。所以本文引入社會資本作為重要影響因素，從而針對建筑施工活動的特殊性做出合理的安全預測。基于安全人機工程學、安全管理學和社會資本理論，本文認為影響建筑施工安全績效的主要因素包括：社會資本、員工安全能力、安全管理、施工設備和材料和環境條件這5個因素。本文在借鑒國內外相關文獻研究[8,9]的基礎上，通過現場訪談的形式確定了相對應的測量量表的維度劃分。在通過專家和課題組對初始量表的討論后，形成了本文調查的最終問卷。問卷共包括三部分內容，第一部分為項目的基本信息，第二部分為影響建筑施工項目安全績效的因素量表，第三部分為被調查者的基本信息。題項采用李克特量表五分法，用非常不同意（1分）到非常同意（5分）來表示。本文在北京、天津、河北、河南、四川、江蘇、山東等省份及直轄市進行問卷調查，調查對象包括建設施工單位的項目經理、副經理、安全經理、安全員、工長。本次問卷發放數量為360份，涉及15個省共90個項目，對無效問卷進行剔除后得到有效問卷300份，問卷有效率為83%。

采用Cronbach's α系數來檢驗量表的信度，結果顯示各量表的Cronbach's α系數均高于0.8，量表整體的信度達到0.923，表明此項研究的量表信度值較高，具有良好的內部一致性。問卷在編制過程和多位專家進行了討論并對題項進行了修改，可以認為量表的內容效度是可接受的。運用AMOS計算各量表的收斂效度即檢驗各潛在變量測量模型的適配度[10]。對各模型進行檢驗的結果顯示：各變量測量模型的測量題項因素負荷量的C.R.值均大于1.96，各測量模型的卡方自由度比值都小于臨界值3，RMESA值都小于臨界值0.08，GFI值都大于臨界值0.9，AGFI值都大于臨界值0.9，均達到模型適配標準，表示測量模型可以與樣本數據契合，說明量表具有很好的收斂效度。

ROSETTA是一種可視化很強易于操作的RS工具。將回收的300份有效問卷的結果作為RS處理的基本數據。根據RS理論將數據中的屬性分為條件屬性和決策屬性，文中數據的條件屬性即影響施工項目安全績效的因素，共54個。決策屬性即被調查者對項目安全績效的總體評價值。首先使用ROSETTA軟件中最高可信度填補法補齊原始數據中缺失的屬性數據，然后采用等頻率劃分算法對問卷數據進行離散化處理，最后采用遺傳算法對條件屬性進行屬性約簡，最終得到35個重要因素，具體的結果如表1所示。

3.2 檢驗結果分析

為判斷安全預測模型的有效性，本文利用前面經過RS處理過的300份樣本數據，選取前200組樣本數據作為模型的訓練數據，然后選取另外100組樣本數據作為測試數據，分別進行歸一化處理。模型的參數設置如下：種群數量為20，迭代次數為200，c1=1.5，c2=1.7，w=1，核函數參數c的變化范圍為[0.1,100]，懲罰參數g的變化范圍為[0.01,1000]。PSO參數尋優的過程如下頁圖3所示。

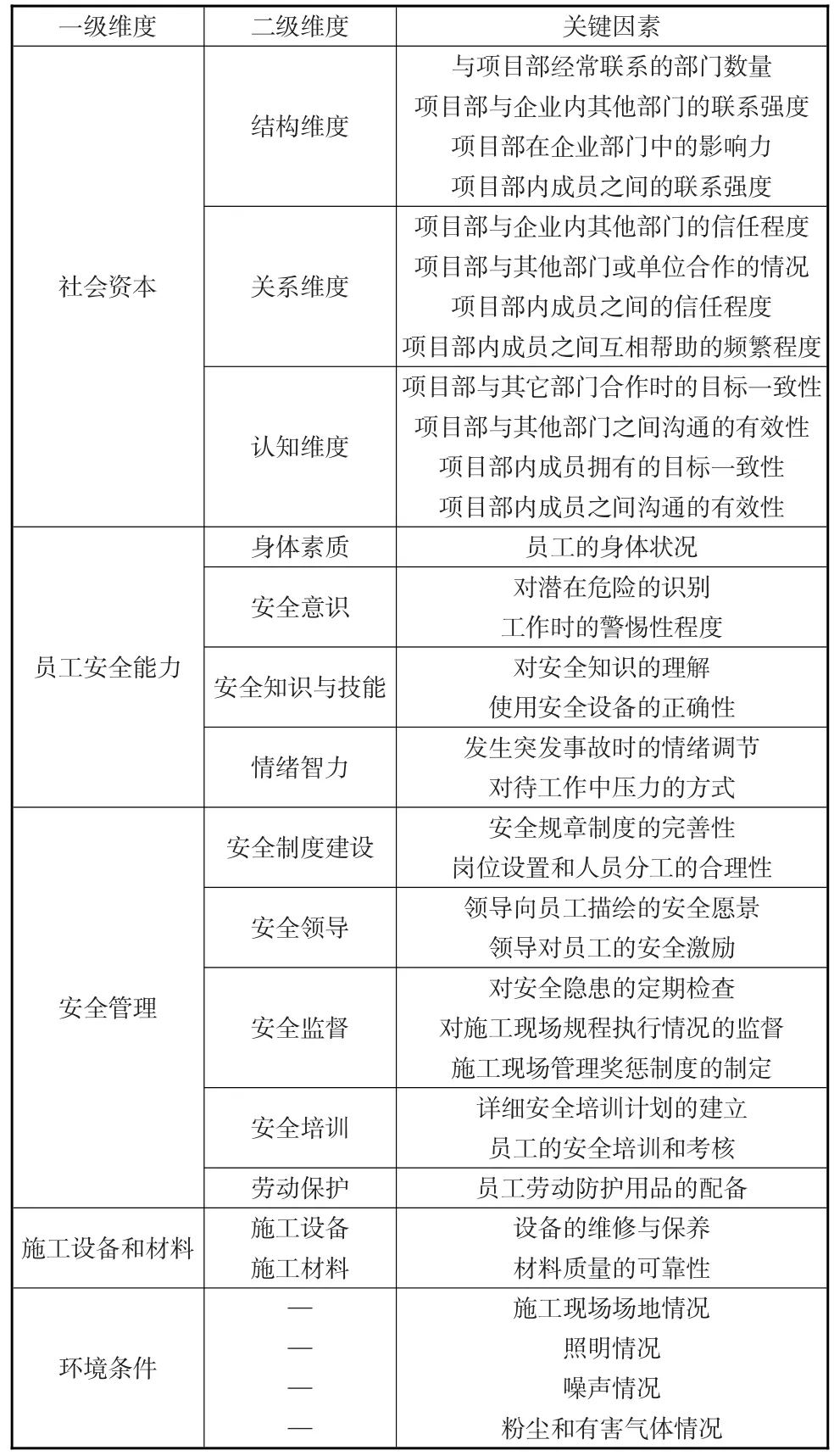
表1 影響建筑施工項目安全績效的關鍵因素

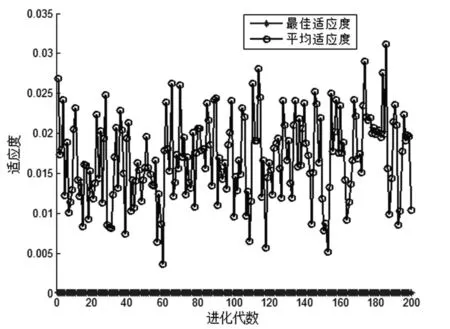
圖3 PSO尋找最佳參數的適應度曲線

從圖3中可看出，參數尋優后得到的最佳參數c=14.6759，最佳參數g=0.01，最佳平均MSE=0.00035982。在確定核函數和參數c、g后，利用LIBSVM對200組樣本數據進行訓練，然后對100個樣本的測試數據進行回歸預測，模型原始數據和回歸預測數據對比圖、誤差圖如圖4所示。

結果顯示該模型預測的MSE=0.000461458，擬合相關系數=99.5853%，精度和擬合度較好。絕對誤差值大多數分布在-0.03到0.03之間，誤差很小。結果表明本模型具有很好的預測效果和泛化能力，也同時證明了關鍵因素篩選的正確性、安全預測模型的有效性和實用性。

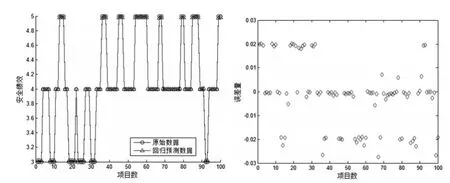
圖4 改進的PSO-SVM模型驗證分析結果

4 結論

（1）本文將改進的PSO算法對SVM中的參數進行優化，通過引入慣性權重的自適應調整和高斯擾動的思想，能有效解決PSO算法陷入局部最優的問題，能增強粒子的逃逸能力，可有效提高模型的訓練速度和預測精度，使模型具有很好的非線性擬合能力，并減少預測誤差。（2）改進的PSO-SVM模型可以有效預測建筑施工項目的總體安全績效。模型學習速度快、預測效果好、泛化能力強、參數設置簡單，在項目安全預測方面有明顯的優勢。實證分析的結果表明該模型具有較高的預測精度和較好的適用性，在建筑施工安全管理中有很好的應用價值。（3）社會資本是影響施工項目安全績效的重要因素。通過調查訪問，利用RS篩選出關鍵要素，通過對模型的仿真模擬和驗證分析，檢驗了社會資本作為關鍵因素的正確性和合理性。社會資本一方面為管理者提供施工安全狀況作為預測依據，另一方面為安全管理政策的執行以及形成良好的安全文化提供了無形的途徑。

[1]肖智,李玲玲.PSO-SVM在高速公路交通量預測中的應用[J].管理評論,2011,23(12).

[2]呂軍,王德運,魏帥.中國石油安全評價及情景預測[J].中國地質大學學報:社會科學版,2017,17(2).

[3]范振東,崔偉杰，郭芝韻等.基于改進的PSO-SVM法的大壩安全非線性預警模型研究[J].水電能源科學,2014,32(11).

[4]艾兵,董明剛.基于高斯擾動和自然選擇的改進粒子群優化算法[J].計算機應用,2016,36(3).

[5]Kumar N,Vidyarthi D P.A Model for Resource-constrained Project Scheduling Using Adaptive PSO[J].Soft Computing,2016,(20).

[6]王小川,史峰,郁磊.MATLAB神經網絡43個案例分析[M].北京：北京航空航天大學出版社,2013.

[7]邊燕杰,丘海雄.企業的社會資本及其功效[J].中國社會科學,2000，(2).

[8]Koh T Y,Rowlinson S.Project team Social Capital,Safety Behaviors,and Performance:A Multi-level Conceptual Framework[J].Procedia Engineering,2014,(85).

[9]Cheng E W L,Ryan N,Kelly S.Exploring the Perceived Influence of Safety Management Practices on Project Performance in the Construction Industry[J].Safety Science,2012,50(2).

[10]吳明隆.結構方程模型——AMOS的操作與應用[M].重慶:重慶大學出版社,2010.