力的合成實驗研究:改進、爭論與反思

馬亞鵬

(銀川市第九中學,寧夏 銀川 750011)

力的合成是高中物理中重要的學習內容,平行四邊形定則是矢量運算的基本法則,在物理學中具有舉足輕重的地位．因此,如何優化力的合成教學是值得探討的問題,其關鍵是力的合成實驗的教學處理．本文通過綜述力的合成實驗研究的成果,對幾個引起爭議的問題進行深入的反思．

1 力的合成實驗方案及其改進

1.1 力的合成實驗的基本方案

教科書中的力的合成實驗有以下兩種方案.

方案1： 研究力的合成.[1]

圖1 實驗方案1

圖1甲表示橡皮條GE在兩個力共同作用下,沿著直線GC伸長了EO這樣的長度．圖1乙表示撤去F1和F2,用一個力F作用在橡皮條上,使橡皮條沿著相同的直線伸長相同的長度．力F對橡皮條產生的效果跟力F1和F2共同產生的效果相同,所以力F等于F1和F2的合力．

合力F跟力F1和F2有什么關系呢?在力F1和F2的方向上各作線段OA和OB,根據選定的標度,使他們的長度分別表示力F1和F2的大小(圖1丙)．以OA和OB為鄰邊作平行四邊形OACB．量出這個平行四邊形的對角線OC的長度,可以看出,根據同樣的標度,合力F的大小和方向可以用對角線OC表示出來．

改變F1和F2的大小和方向,重做上述實驗,可以得到同樣的結論．

方案2： 驗證力的平行四邊形定則.[2]

(1) 把橡皮條的一端用圖釘固定在A點,另一端用兩根細線打一個結點B,兩根細線分別掛上一只彈簧測力計,如圖2(a)所示．

(2) 分別用力F1和F2拉兩測力計,把結點B拉伸到O點,如圖2(b)所示．記下O點的位置,先記下此時F1和F2的大小和方向,再用力的圖示法將它們表示出來．

(3) 撤去一只測力計,只用一個力F拉測力計,同樣將結點B拉到O處,如圖2(c)所示．記下F的大小和方向,并用力的圖示法表示．

(4) 改變F1、F2,重復實驗．

圖2 實驗方案2

比較F1、F2和F的大小與方向,驗證F1、F2與F是否滿足平行四邊形定則．

1.2 兩種方案的比較

兩種方案實際上都采用等效替代的思想方法,在力F能夠等效替代F1、F2的前提下,尋找它們之間的關系．仔細研習教科書文本可知,兩種方案均是驗證性實驗的設計思路．比較而言,方案1現象明顯、形象直觀,適合做演示實驗．方案2取材簡易,是中學物理中的常規實驗之一,適合做學生分組實驗,有助于培養學生的實驗操作能力．

兩種方案又各有不足:方案1中,3個力的大小一般情況下很難保證符合整數比(即鉤碼個數為整數且效果等效),因此,教師在教學處理時往往采用兩分力垂直的情況下,如圖1中3個力的大小之比為3∶4∶5．此外,要做好這一演示實驗,需要在課前反復實驗并標記位置,且改變力的大小重新演示時儀器操作和調整極其麻煩．方案2在課堂教學情境下,往往耗時較多(課堂觀察結果發現,往往學生動手實驗占掉大部分時間,則導致“分析與論證”環節草草收場)．另一方面,實驗室用彈簧測力計精度大,測量誤差大,導致實驗結果與預期不符．

1.3 對實驗方案的改進

由于兩種方案均有不足,對其進行改進引起了一線教師極大的興趣,也提出了不少有價值的改進方案,現舉幾例分析如下.

改進方案1： 采用沙筒、沙粒,天平配合鉤碼進行實驗,具體做法如下.[3]

圖3 改進方案1

如圖3所示,G和L1、L2、L3為帶有吸盤的掛鉤和定滑輪,P為沙和沙筒．實驗中可以通過任意移動定滑輪位置改變F1、F2和F的方向,在圖3甲中通過改變鉤碼的個數,即改變F1、F2的大小,在圖3乙中通過改變鉤碼的個數和沙粒的質量以達到改變F的大小,從而實現調節的目的．

圖4

這一改進方案對3個力的大小沒有必須是整數比的約束,通過用天平測量沙與沙筒的質量,進而得出合力F的大小,對精確驗證平行四邊形定則打下基礎．但是這一改進并未解決多次測量時儀器調整不便的問題．

改進方案2： 另一個改進方案如圖4所示,[4]在一底座上固定兩根豎直的金屬桿,在桿的上端固定兩個定滑輪A、B．演示時,先用一根繩子懸掛重物,平衡時繩子對重物的拉力等于鉤碼的重力．再分別將兩根繩子一端連在重物上,另一端跨過A、B兩個定滑輪后掛鉤碼將重物吊起,平衡時兩個拉力分別為F1和F2．F1和F2共同作用效果與F單獨作用效果相同．最后通過力的圖示研究三者的關系,得出結論．

這一改進方案實際上巧妙運用了3力平衡的規律．其優點是儀器組裝方便,只要懸掛在滑輪兩側的鉤碼的數量合適,總能夠找到在某一角度下兩個力的合力與第三個力等效．實驗操作也方便,但是從教學的角度,三力平衡屬于后面的內容,學生在未對平行四邊形定則和共點力作用下物體的平衡條件有深入理解的情況下,理解實驗原理存在困難．

改進方案3： 還有人自制了力的合成演示儀,[5]示意圖如圖5.

改進方案3利用滑槽(可固定木板)、弧形槽(可改變分力的方向)、固定螺桿和螺母(可將滑輪固定在弧形槽中任意位置)等制成演示儀．演示時,可將白紙貼在木板上并將木板插入立柱的豎直槽內．在與掛橡皮條的釘子(圖中5)相平的位置安裝一定滑輪,用幾個鉤碼拉橡皮條使之伸長至某一長度并標記．分別在弧形槽中插入定滑輪,并分別將兩細繩套通過定滑輪掛上鉤碼,緩慢移動弧形槽中滑輪的位置,直至橡皮條也拉伸到同一長度．記錄鉤碼的數量,標記兩繩子的方向．最后用力的圖示作圖研究3個力之間的關系．

1. 底座 2. 立柱 3. 木板 4. 定滑輪 5. 釘子 6. 橡皮條 7. 鉤碼 8. 固定螺桿 9. 弧形槽

圖5 改進方案3

這一改進方案的優點是可以根據需要任意移動滑輪位置以改變分力的方向,可增減鉤碼的數目以改變兩分力的大小,實驗完成后可將白紙取出進行嚴格的作圖,兼顧了演示的直觀性和作圖的精確性,還可以做多次實驗,便于歸納總結出力的合成規律．然而,因為用鉤碼的重力來確定力的大小,使得分力不能連續變化,實際實驗時往往也是選擇特殊的情況進行,缺乏普遍性．這也是上述幾個改進方案的共性不足．

圖6 改進方案4

改進方案4： 針對上述實驗的不足,有人提出利用現代信息化實驗手段進行實驗,[6]如圖6,利用Dislab力傳感器及其配套的力矩盤、鉤碼等器材獲取精確的實驗數據,并通過數表軟件處理數據得出實驗結論．

由于傳感器的數據系統本身是按照平行四邊形定則設計的,當輸入力傳感器的讀數和兩個分力之間的夾角后,數據處理系統立即會計算出合力的理論值,進而比較理論值和實驗值,驗證力的平行四邊形定則．該實驗運用現代技術進行探究,實驗方案新穎,能夠吸引學生的注意力,有助于激發學生的學習動機和探究熱情．另外,該實驗精度高、現代技術與物理課程深度融合,有助于培養學生的創新能力．這個實驗一方面基于3力平衡原理設計,另一方面多數學校由于實驗設備所限無法全面推廣．

2 力的合成實驗的3大論爭

(1) 實驗方案的驗證與探究之爭.

《普通高中物理課程標準(實驗)》對本節內容的要求為“通過實驗,理解力的合成與分解”,[7]但并未規定是驗證性實驗還是探究性實驗,在實踐中則出現了驗證與探究之爭．首先表現在人教版新教材明確采用科學探究的思路呈現教學內容,將傳統的驗證性實驗方案2改為探究性實驗．[8]其次,在一些優質課比賽中,多數采用科學探究實施教學,并且探究的實施較為到位、效果良好．[9]但也有一些人認為力的合成教學不宜采用探究式教學．持這種觀點的人認為,平行四邊形定則的探究難度大,且現有的實驗方案并不能很有效地得出實驗結論．

將科學探究作為重要的學習內容和學習方式引入高中物理教學是發展學生的物理學科核心素養具有重要途徑,教師在教學中應根據學習目標與內容的特點、學生的能力與情感特征和教學條件等因素合理確定探究教學的目標、內容和方法．將驗證性實驗更改為探究性實驗是科學探究的一種常見形式．因此,力的合成實驗教學完全可采取科學探究的思路進行,問題的關鍵是如何提高探究的質量．

(2) 實驗方法的傳統與現代之爭.

在實驗方法上,上述實驗方法除改進方案4外,均屬于傳統的實驗方法．改進實驗4用到了傳感器技術,屬于現代實驗方法．除此之外,還有一些現代實驗方法．如有人用幾何畫板的追蹤功能將兩個彈簧秤的拉力及夾角之間變化曲線定量地描繪出來,直觀展示物理量的變化過程．[10]還有人用GeoGebra軟件的矢量功能輔助力的合成教學,[11]即在運用實驗得出平行四邊形定則后,運用該軟件動態、直觀的特性幫助學生深入理解合力和分力之間的關系．

在現代技術尤其是作圖軟件、數據分析軟件日新月異的今天,數字仿真實驗、虛擬實驗等備受青睞并被大量運用于課堂教學之中,大有替代真實實驗的態勢．仿真實驗、虛擬實驗在學生對物理過程等缺乏直觀感性認識的情況下有其積極的作用,畫圖工具尤其是數值分析軟件確實對一些復雜物理問題的解決提供了便利．正如任何技術的使用都有其邊界條件,這些類型的實驗替代不了傳統實驗,這是因為實驗提供給學生一個純化的物理操作環境,通過操作獲取和建構知識、發展思維能力、培養求真精神．而用幾何畫板等軟件在處理力的合成問題是以平行四邊形定則為理論設計的“程序”,不論具體的力的數值如何變化,其運行結果總是符合平行四邊形定則的,這里只有確定性的數學,在本質上與物理實驗的精神是相悖的．

(3) 數據處理中理論值與實驗值之爭.

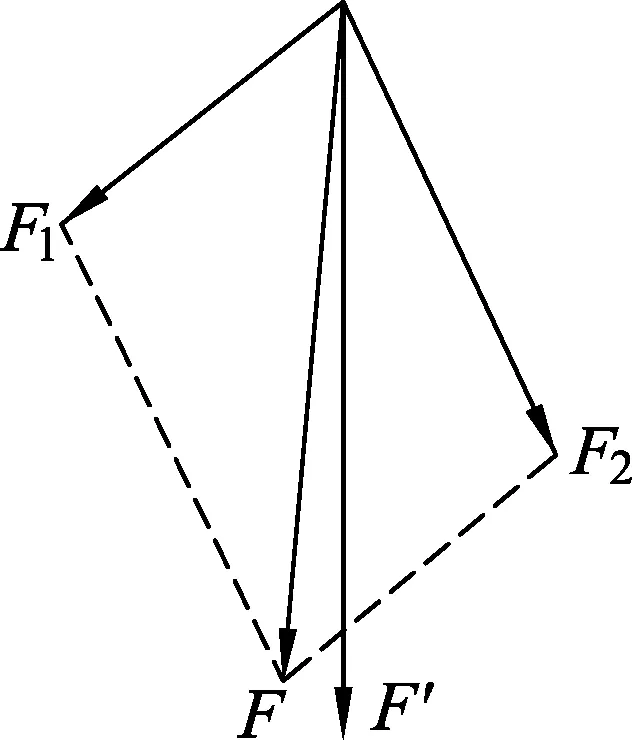
圖7 數據處理示意圖

實驗方案2中,用一只彈簧秤測得的力F′為合力的理論值,還是用平行四邊形定則畫出來的對角線F為合力的理論值,這也是一個有爭議的問題,如圖7．有人認為前者是理論值,[12]理由是“此實驗是驗證力的平行四邊形定則,所以力的平行四邊形定則暫不能認為是正確的理論,但是那一個力就是那兩個力的合力,這個理論一定是正確的,所以能真正替代F1和F2共同作用效果的是用彈簧秤拉出來的那個力F′,而F是在實驗過程中平行四邊形對角線這樣一個實驗操作得到的,所以是實驗值”．反對者則認為,“我們要驗證的是力的平行四邊形定則,那根據這一理論得到的F′自然是理論值了;而為了驗證這一理論,根據合力的定義,我們用一根彈簧秤去拉橡皮條,得到的F就應當是實驗值”．[13]還有人在區分真實值、實驗值和理論值的基礎上,認為上述兩種觀點都是錯誤的,正確的觀點應該是“驗證力的平行四邊形定則時的F和F′都是實驗值(測量值),其中F′是間接測量值,F是直接測量值”．[14]

對實驗值和理論值的爭論陷入迷津之中，通俗地講，理論值是理論導出來的數字，實驗值是實驗中測定的數據.仔細考查力的合成實驗本身可以發現，實驗的目的是尋找求合力的方法或驗證力的平行四邊形定則，即確定或驗證力的合成也遵循平行四邊形定則這一矢量合成所遵循的運算法則.在實驗中，用一只彈簧秤拉橡皮條和用兩只彈簧秤產生的效果相同，則這一只彈簧秤的讀數F′即為兩個分力的合力，用這種方式直接測量合力，是等效替代思想方法的運用，符合物理原理，可認為在這個實驗中，這一測量值是較為準確的.根據分力的圖示運用平行四邊形定則畫出對角線，并測量出合力F，顯然是間接測量.最終，需要對兩個測量結果進行比對，若二者在實驗誤差允許的情況下測量結果一致，便確證力的合成的確遵循平行四邊形定則.因此，F和F′都是實驗值，是依據不同方法展開的具體測量，這里沒有理論值，上述第三種觀點是正確的.

3 對力的合成實驗研究的反思

(1) 對力的合成實驗改進研究的反思.

自制教具和對已有實驗方案的改進是我國物理實驗教學的優良傳統,但我們也要看到,存在著“為改進而改進”的現象．教學用演示實驗或學生分組實驗的改進應遵循目標明確、原理正確、操作容易、效果明顯、取材便利、設計美觀、簡單輕巧等原則,即替代方案要比原有方案更優化．依據上述原則可以發現,在力的合成實驗的改進方案中,改進方案2和4采用三力平衡原理,不適合高中學生新課學習;方案3構造過于復雜,也缺乏精致與美感．另一方面,在課堂教學中,只要教法得當,采用實驗方案2即可完成教學任務,實則沒有改進的必要．實驗方案2是在多年的教科書編寫修訂中沉淀下來的,有其獨特的教學價值．在沒有“更優”的改進的情況下,與其“挖空心思”創新,還不如深入研究現有方案的教學價值讓其教育功能充分發揮．

(2) 對3大爭論中折射出的問題反思.

力的合成實驗研究中的爭論折射出物理教學研究與實踐中的一些問題．一是教師的教學觀念的問題．教師的教學觀念或教學信念,對教學實踐具有定向作用,探究性實驗和驗證性實驗是物理教學中常見的兩種實驗教學模型,不能厚此薄彼,過分推崇驗證和過分推崇探究的做法都是不妥當的．究竟以何種方式進行實驗教學,有賴于教師對教學目標的預設和對實驗教學價值的體察以及對整個高中階段實驗教學的系統化安排．二是實驗理論研究問題．中學教師對實驗改進、自制教具和實驗習題有較大的興趣,但對實驗的本質、實驗的意義、實驗與理論的關系等的認知和研究尤為不夠,力的合成實驗中的理論值和實驗值之爭充分折射出物理實驗理論(實驗哲學)研究的重要性．

(3) 對本研究的意義反思.

本文以力的合成實驗為個案,系統評析了力的合成實驗方案及其改進,回應力的合成實驗教學中的爭論．在中學物理教學研究中,對某個實驗的各種方案的述評性研究并不多見．此類述評性研究最大的價值是從對實驗方案及其改進之中,逐漸明晰個案實驗的核心特點、相關問題,幫助教師形成適當的實驗教學思路與方法．同時,本研究亦有助于啟發教師在教學中深入思考實驗教學問題,辨識實驗本身的教育價值,窺探到實驗教學的真諦所在．從這個意義上,本研究具有重要的方法論意義．

1 人民教育出版社物理室.全日制普通高級中學教科書物理·必修.第1冊[M].北京:人民教育出版社,2003:12.

2 廖伯琴.普通高中課程標準實驗教科書物理1·必修. [M].濟南:山東科技出版社,2004:88.

3 周峰.“力的合成”演示實驗的操作改進[J].中學物理教學參考,2005(4):51.

4 薛文堂.這樣演示“力的合成”效果好[J].中學物理教學參考,2007(7):32.

5 劉萬強.力的合成演示儀[J].物理實驗,2007(9):23-24.

6 鄧思平.驗證力的平行四邊形定則實驗的改進[J].中學物理教學參考,2015(5):71-72.

7 中華人民共和國教育部.普通高中物理課程標準·實驗[S].北京:人民教育出版社,2003:13.

8 人民教育出版社物理課程教材研究開發中心.普通高中課程標準實驗教科書物理1·必修.第3版[M].北京:人民教育出版社,2010:62.

9 陸永華.關于“力的合成”的省優質課觀摩的思考[J].物理教師,2014(10):71-73.

10 高建勇.用幾何畫板對“力的合成”的探究[J].物理教師,2006(4):48.

11 黃北京,劉毓球.用GeoGebra的矢量功能輔助力的合成教學[J].物理通報,2013(5):96-98.

12 張乃劍. “驗證力的平行四邊形定則”實驗中理論值與實驗值的思考[J].物理教師, 2009(1):18.

13 陳毓華. 再論“驗證力的平行四邊形定則”中理論值與實驗值[J].物理教師,2011(9):38-39.

14 孫鐵斌. 談“驗證力的平行四邊形定則”中理論值與實驗值[J].物理教師,2016(9):57-59.