兩絕緣線懸掛兩帶電小球靜止時的不變量

趙 軍 李 力 蔡源園

(1. 重慶市清華中學,重慶 400054; 2. 重慶市融匯清華實驗中學,重慶 400054)

如圖1(a)所示,兩絕緣細線懸掛兩同號帶電小球,如果靜止時兩球位于同一高度,容易證明m1tanθ1=m2tanθ2,即m·tanθ是不變量.于是偏角大小與兩球帶電荷量無關,且質量大則偏角小,反之亦然,這是眾所周知的結論.

進而考慮如圖1(b)的兩細線長度相等的情況,偏角是否仍然僅與質量存在上述關系?

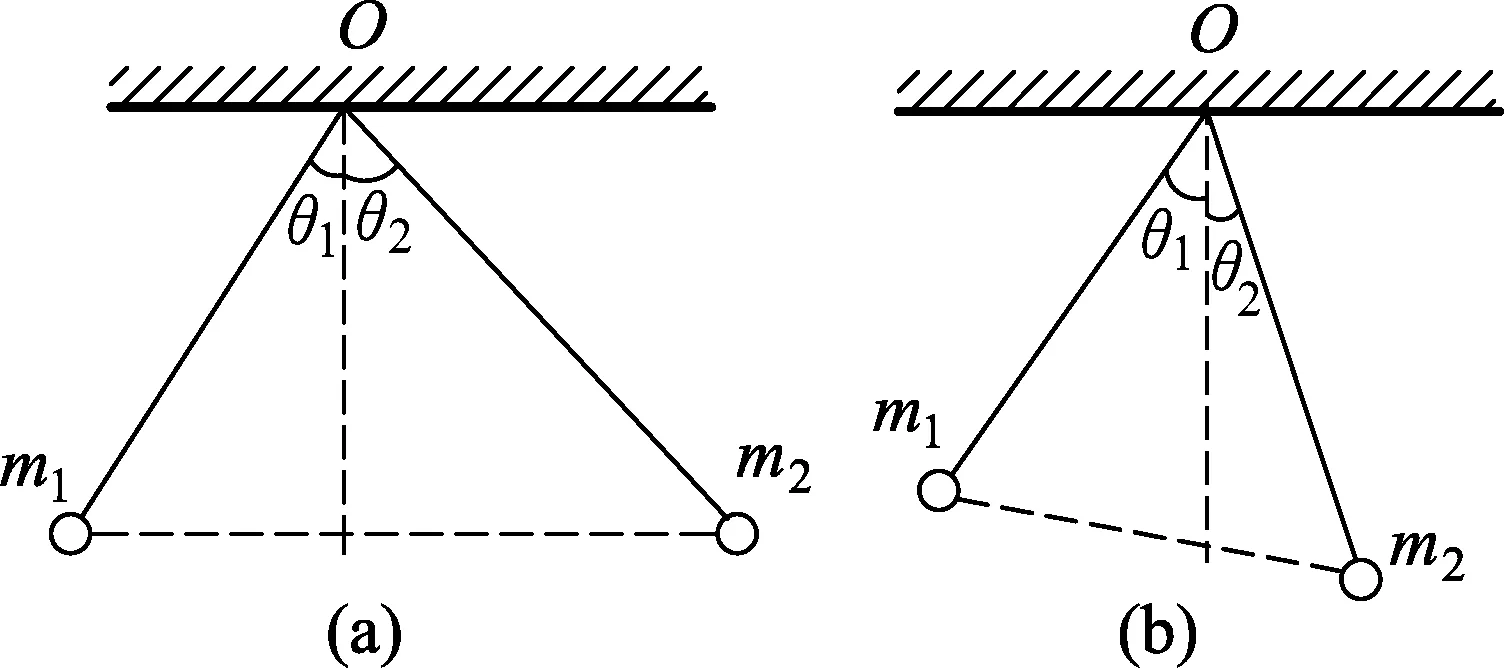
圖1

對此也不難用平衡條件(比如拉密定理)推得m1sinθ1=m2sinθ2,即m·sinθ是不變量.同樣有“偏角大小與兩球帶電荷量無關,且質量大則偏角小,反之亦然”的結論.

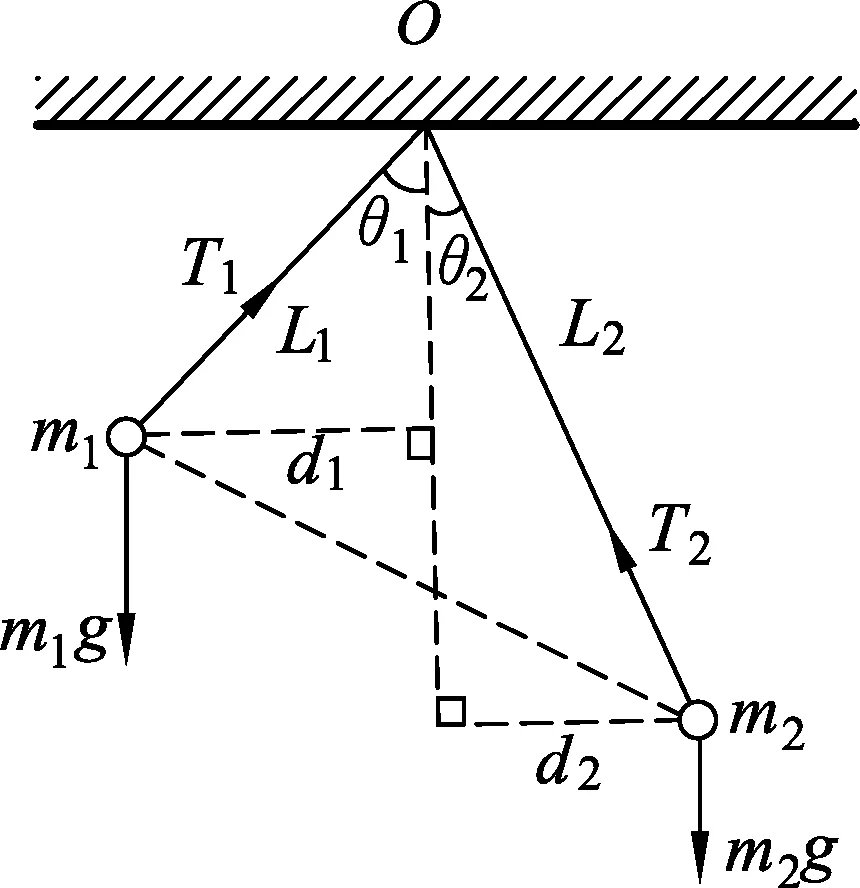
圖2

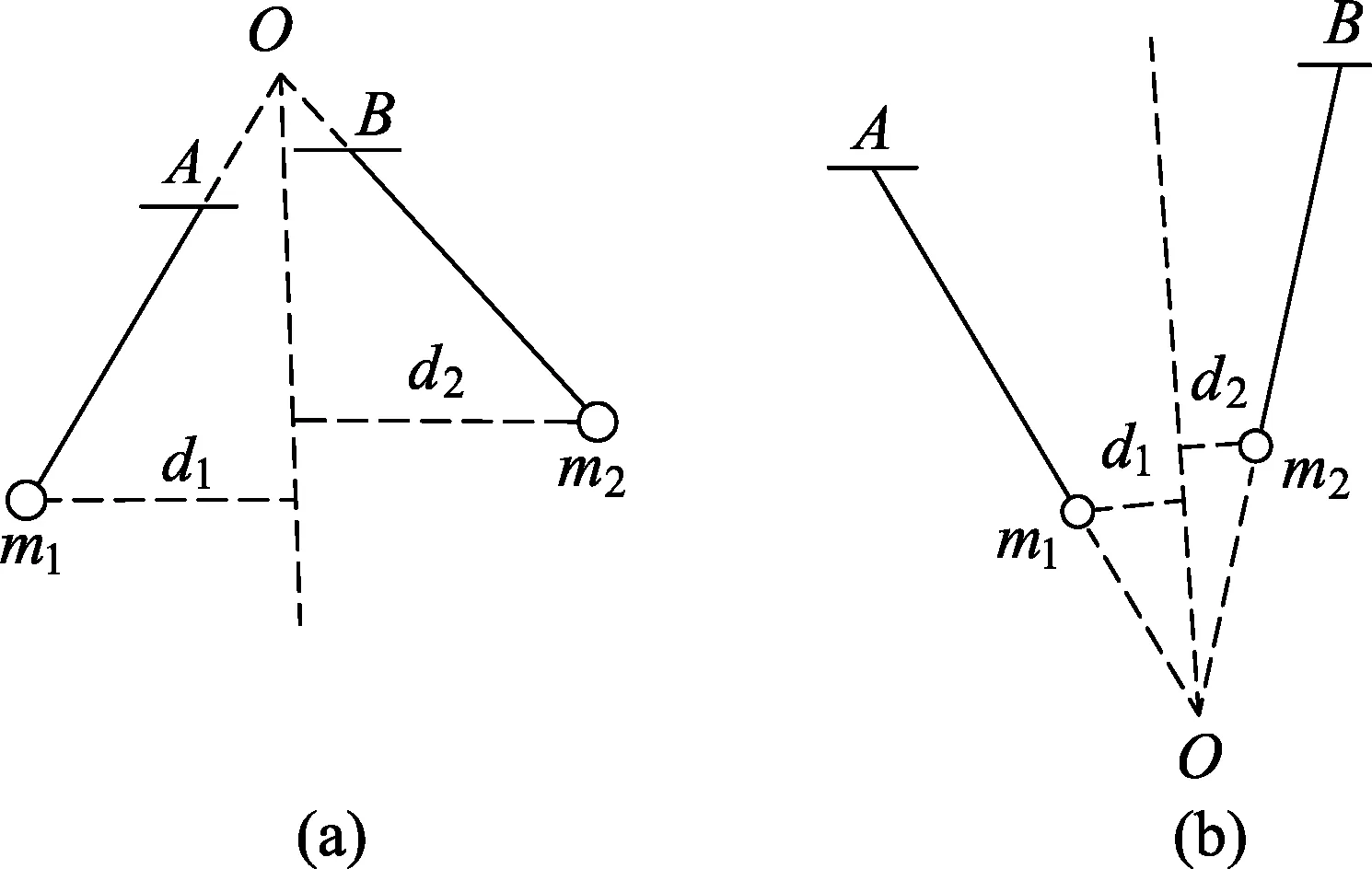
于是不禁要問:如果線長不等(分別為L1,L2)且靜止時兩球亦不在同一高度,如圖2所示,那么還有此結論么?這種一般情況下不變量又是什么呢?

這時再逐個研究單個小球的平衡,就稍嫌繁瑣了．因兩小球均平衡,則體系所受外力對O點的力矩代數和應該為0．兩球間的庫侖力是一對內力,而線對球的拉力均過O點從而力矩為0,故有m1L1sinθ1=m2L2sinθ2,可見不變量是m·Lsinθ.雖然偏角大小仍然與兩球帶電荷量無關,但是“質

量大則偏角小”不再成立,因為還與線長有關．容易看出,在靜止時兩球位于同一高度或線長相等的條件下,不變量m·Lsinθ分別轉化為m·tanθ、m·sinθ,這說明圖1的兩種情況是特例.

由于線長不等,同號兩球排斥作用產生的偏離程度,顯然不能用線與豎直方向的偏角大小來表示了．注意到d=Lsinθ,故不變量可寫成m·d,d為靜止時小球到過懸點O的豎直線的距離(如圖2),它正是這種一般情形中代替偏角描述小球偏離程度的幾何量.所以,得到如下普遍成立的定理.

定理:兩絕緣線同懸點懸掛兩帶電小球靜止時,小球質量與其到過懸點的豎直線的距離的乘積m·d是不變量,與小球帶電荷量無關．

此結論還可推廣,當兩同號帶電小球懸掛點不同甚至不等高時[如圖3(a)],或者兩異號帶電小球相吸引的情況[如圖3(b)],上述結論也是成立的.因為取兩線延長線的交點為O點,則前面的證明過程同樣是成立的.不過必須提醒的是,這時d應該是靜止時小球到過O點豎直線的距離(如圖3)．這樣,在圖3(a)中因d1m2;圖3(b)因d1>d2,則m1

圖3