基于盲信號處理的MIMO雷達對抗

湯永浩，孫建東，黃和國，王成海

(中國航天科工集團8511研究所，江蘇 南京 210007)

0 引言

MIMO雷達由于其發射波形多樣性帶來的額外自由度，能夠提高系統目標檢測、參數估計以及抗干擾等性能[1-2]。根據陣元配置，MIMO雷達可分為：集中式MIMO雷達和分布式MIMO雷達。集中式MIMO雷達陣列配置與傳統相控陣類似，且同時發射不同的信號波形。利用波形多樣性信息，集中式MIMO雷達在接收端能夠依靠信號傳輸通道的正交性，獲取額外自由度，形成虛擬大口徑天線以提高雷達的空間分辨率[3]。分布式MIMO雷達的發射和接收陣元的間距都很大，可認為每個陣元發射的信號之間都是相互獨立的。這種配置的MIMO雷達能夠收集目標的空間多樣性信息，緩解由于目標閃爍引起檢測性能下降等問題[4]。

盡管目前針對MIMO雷達的研究仍然處于理論研究為主、少量實驗室驗證階段，但已有不少學者在MIMO雷達對抗方面展開了相關研究工作。文獻[5～6]對MIMO系統的盲源個數估計進行了研究。文獻[7]等基于盲信號分離提出了對MIMO雷達信號的偵察與識別方法，但并未考慮噪聲的影響。針對MIMO雷達信號的多樣性與復雜性，本文開展了MIMO雷達偵察與干擾技術初步研究，給出了一種基于盲信號分離的MIMO雷達對抗分布式系統的原理框架，初步研究了該框架下的MIMO雷達信號分選識別方法。同時，介紹了利用盲信號處理的結果、結合數字射頻存儲(DRFM)技術，對單雙基地MIMO雷達進行有效欺騙干擾的可行手段，并給出了仿真結果。

1 信號模型

MIMO雷達的概念起始于通信理論中的多通道模型，與傳統雷達的顯著區別在于其不同的陣元能夠發射任意的波形、接收陣元能夠同時處理接收到的不同信號(通常為正交信號)。不妨假設一部具有M個發射陣元和N個接收陣元的MIMO雷達，天線發射任意信號sm(t),m=1,…,M。同時，假設空間遠場位置存在一個目標，則MIMO雷達接收回波信號模型可以描述為：

y(t)=αGKTs(t)+n(t)

(1)

式中，α為目標散射系數，G為N×1維接收通道傳輸系數，K為M×1維發射通道傳輸系數，s(t)=(s1(t),s2(t),…,sM(t))T為M維信號矩陣，n(t)為N×1維噪聲向量。值得注意的是，式(1)為MIMO雷達的通用信號模型，對于集中式和分布式MIMO雷達，其區別在于G和K的定義不同。對于集中式MIMO雷達而言，G和K即為明確可知的相應陣列天線的接收和發射導向性矢量。

類似地，不妨假設MIMO雷達偵察系統具有N個接收機，參考式(1)可得偵察系統的輸出信號為：

y(t)=Hs(t)+n(t)

(2)

式中，H為N×M維傳輸通道系數矩陣。比較分析式(1)和式(2)可知，MIMO雷達偵察系統盡管具有與MIMO雷達相似的信號模型，但是雷達信號s(t)與傳輸矩陣H均為未知數。對于MIMO雷達對抗系統來說，不僅要能判斷出是否為MIMO雷達體制，而且還要能夠掌握MIMO雷達的具體細節，如信號參數、陣列配置等，從而對MIMO雷達實施有效干擾，其關鍵在于對MIMO雷達波形的分選與識別。因此需要突破常規雷達信號偵察手段，對混疊在一起的復雜MIMO雷達信號進行盲分離處理。

2 MIMO雷達盲信號分離問題

2.1 問題建模

近年來，盲信號處理算法已經在無線通信、語音處理、神經網絡等方面有了廣泛應用研究。“盲”主要指源信號及其混合方式均未知，而盲信號處理算法則是指僅依靠觀測獲得的混合數據恢復出源信號及其混合矩陣的一類算法。按照源信號混合方式，盲源分離研究可分為瞬時線性混疊、卷積混疊及非線性混疊盲分離3類。MIMO雷達信號的盲分離恰恰屬于最簡單的瞬時線性混疊方式，其模型為：

y(t)=As(t)

(3)

x(t)=Wy(t)

(4)

式中，s(t)為未知源信號矩陣，A為混合矩陣，y(t)為已知觀測信號矩陣，W為分離矩陣，x(t)為分離信號。理想情況下，滿足W=A-1，即意味著能夠獲得未知源信號的最佳估計。

目前關于盲源分離算法研究很多，本文主要分析超定盲分離的情況。獨立成分分析(ICA)是求解超定盲分離問題的成熟算法，針對MIMO雷達信號盲分離問題的求解有以下要求限制：

1) 源信號的各個分量為相互統計獨立的零均值平穩隨機變量；

2) 混合矩陣列滿秩，且觀測信號維數不少于源信號維數；

3) 混合信號中最多只能有一個高斯分量。

在滿足上述3個條件的假設下，ICA算法能夠實現對源信號的分離及混合矩陣的估計。MIMO雷達通常發射正交波形，這是MIMO雷達的顯著特征，因此條件1)顯然滿足。為了滿足條件2)，可以采用分布式多接收站來實現，即在空間不同位置進行多點采樣，利用空間分集特性獲得列滿秩的混合矩陣，同時節點數需要大于源信號數。比較式(2)和式(3)模型可以發現，對MIMO雷達盲信號處理問題應用ICA算法，無法避免高斯噪聲帶來的影響，并且高斯噪聲維數與觀測信號維數相同，因此無法滿足條件3)。不妨對式(2)中的MIMO雷達偵察信號模型進行一定的變換，即改寫為：

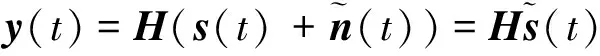
(5)

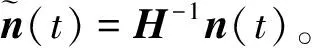
2.2 盲信號分離算法

目前盲信號分離的算法較多，其中快速不動點ICA算法(FastICA)具有收斂速度快、精度高等特點，因此本文以FastICA算法為例簡要分析。基于FastICA算法[8]的MIMO雷達盲信號分離算法如下：

1) 對觀測數據進行降噪或降維處理，利用PCA、MDL或AIC等準則[9]估計獨立成分個數m；

2) 對數據進行白化處理，并選擇非高斯性度量函數為gy=y3；

3) 選擇具有單位范數的初始化向量wp(隨機選擇)；

5) 對分離向量進行正交化和標準化：

6) 如果wp尚未收斂，返回步驟4)；

7)p=p+1，若p≤m，返回步驟4)；

8) 計算分離信號x(t)=Wy(t)，W=(w1,w2,…,wm)T。

3 基于盲信號處理的MIMO雷達對抗系統,

3.1 系統架構

基于盲信號處理的MIMO雷達對抗系統示意框圖如圖1所示。該系統采用N個接收機對MIMO雷達進行信號偵收，其具體實現方式可以為分布式布陣，如無人機集群偵察系統，也可以由一架偵察飛機在飛行路徑中的多個位置進行多次分時采樣獲得。截獲數據可采用分布式或集中式進行處理。根據盲信號處理的結果，對分離出的信號分別進行聚類、融合等處理。根據偵察處理結果，結合數字射頻存儲(DRFM)技術，可對干擾信號的各獨立分量進行單獨調制，實現對MIMO雷達的所有通道進行有效干擾。若綜合考慮不同信道的相關性，合理調制各個干擾分量，可實現對MIMO雷達在時間和空間上具有良好相關性特征的欺騙式干擾。

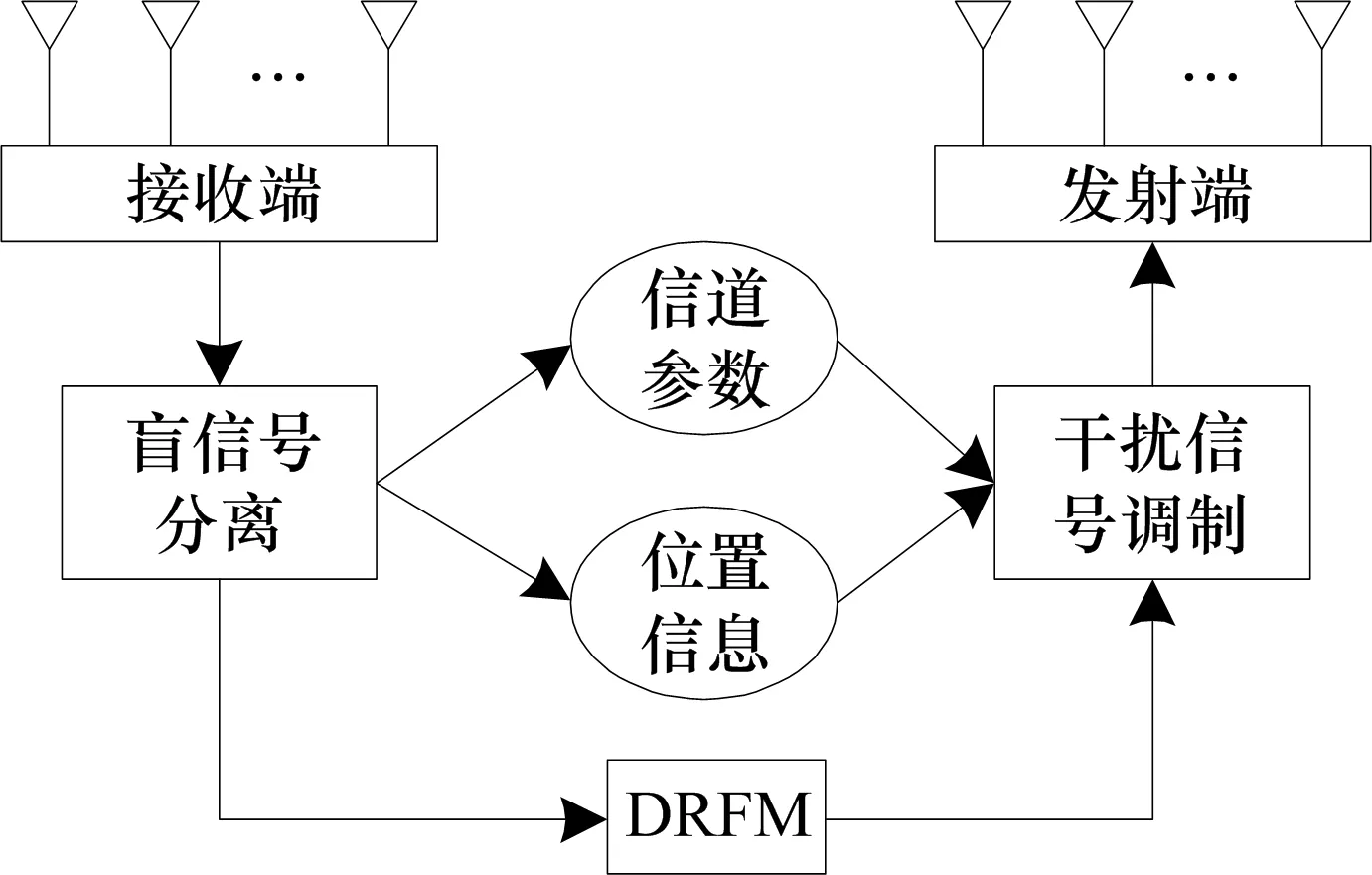
圖1 基于盲信號處理的MIMO雷達對抗系統示意圖

該系統對MIMO雷達的對抗處理步驟如下：

1) 對截獲的信號經由盲信號分離模塊處理，提取各個信號的頻率、脈寬、幅度、波形調制等信息；

2) 對信號脈沖參數進行分選，對輻射源進行識別、定位等計算；

3) 通過信號相關性和信道估計，判斷MIMO雷達工作體制和模式；

4) 判斷MIMO雷達威脅程度，選擇合適的干擾方式和樣式進行干擾；

5) 監測MIMO雷達信號變化，調整干擾策略。

3.2 基于分離信號的MIMO雷達識別

按照目前理論研究的主流觀點，MIMO雷達主要有集中式和分布式兩大類。兩種MIMO雷達無論是在陣列布局和發射波形，還是在接收信號處理方式上，都存在著明顯的差別。其中，分布式MIMO雷達各個發射陣列分布范圍較廣，其發射信號的正交性可以由頻率分集、空間分集或波形分集等得以保證。集中式MIMO雷達在傳統相控陣雷達的基礎上發展而來，因此其發射陣列與相控陣類似，但是其仍然可能被布置成單基地或雙/多基地雷達。此外，傳統的集中式MIMO雷達每個陣元發射正交信號，但是近年來有不少研究學者提出了發射部分相關信號的MIMO雷達體制，因而集中式MIMO雷達具有發射功率均勻分散的搜索模式和發射功率相對集中的跟蹤模式兩種工作模式。因此，對抗方若要對MIMO雷達實施精確、有效的干擾，必須要先對截獲的信號進行仔細分析，對雷達工作體制及工作模式進行識別。

采用圖1所示的處理框架，分離出MIMO雷達所采用的所有正交波形，依據正交波形數量即可推斷出MIMO雷達采用的通道數(陣元天線或子陣數量)。對分離出的單個正交波形進行單獨檢測，利用多站點時差定位、交叉定位等技術，則可對相應的發射陣列天線位置分別進行估計。融合所有定位結果，可判斷MIMO雷達屬于集中式還是分布式配置；同時，定位結果還可以幫助對抗方進行精確、有針對性的電子干擾。此外，利用分離矩陣對發射信道參數的估計，還能夠判斷集中式MIMO雷達的工作模式。這是因為集中式MIMO雷達工作于搜索模式時，雷達能量信號空間均勻分散，信噪比較低，信道參數變化不大；而當其工作于跟蹤模式時，波束具有高增益，信道參數與角度信息具有強相關性。

3.3 單雙基地MIMO雷達的干擾

單雙基地MIMO雷達體制上屬于集中式MIMO雷達，因而具有與相控陣類似的天線陣列結構。該體制的MIMO雷達在搜索模式時，通常采用正交發射波形，發射端不進行波束形成，而在接收端進行接收波束形成和虛擬發射波束形成，稱之為收發聯合波束形成。這種MIMO雷達最為顯著的一個優勢為：能夠利用發射信號傳輸通道的正交性，進行收發聯合波束形成，獲得更大的虛擬口徑，以提高系統的角度分辨率。其點目標接收信號模型可以表示為：

z(t)=αbθraT(θt)s(t)+n(t)

(6)

式中，α為目標散射系數，b(θr)為接收陣列導向性矢量，θr為目標相對接收陣列的方位角，a(θt)為發射陣列導向性矢量，θt為目標相對發射陣列的方位角。通過對接收信號z(t)進行適當處理，如MUSIC、ESPRIT算法等，可以獲得對目標方位角θt和θr的準確估計。

分析式(6)可以發現，若采用傳統調制轉發式欺騙干擾，即對混合信號aT(θt)s(t)進行調制轉發，調制系數將會與散射系數α類似，不會對MIMO雷達的DOA和DOD估計造成影響。而采用本文提出的盲信號處理架構，可實現對所有正交信號通道進行單獨調制，即對s(t)的每一行元素進行不同的調制，即MIMO雷達接收到的干擾信號模型為：

z(t)=αb(θr)(a(θt)diag(φ1,φ2,…,φM))Ts(t)+n(t)

(7)

式中，φm表示對m個正交信號的調制系數。由式(7)可知，發射導向矢量受到干擾調制系數的影響，MIMO雷達的DOD估計將會產生較大誤差，從而收發聯合波束形成將會受到較大的角度欺騙干擾影響。

4 數值仿真分析

本節從數值仿真上驗證MIMO雷達對抗系統采用盲信號處理及角度干擾的有效性。

假設一集中式MIMO雷達采用M=4個發射接收陣元，發射頻分正交線性調頻信號，起始頻率分別為10MHz，每個信號間隔5MHz，帶寬均為4MHz，脈寬為80μs，信噪比設置為20dB。偵察方采用N=5個接收站進行分布式偵收，采用2.2節中的算法對混疊的MIMO雷達信號進行盲分離。圖2～4分別給出了MIMO雷達源信號、某路接收到的空間混合信號以及盲分離后的信號的時頻分析結果。為了方便比較，圖2和圖4中將4路正交信號拼接畫在了同一圖中。分析可知，盡管分離信號的順序與原始信號不一致，但是該算法能夠在源信號和混合矩陣均未知的情況下，較好地實現信號分離，并且從圖5可知，分離信號保持了較好的自相關性(如圖5(a)～(d)所示)和互不相關性(如圖5(e)～(j)所示)。

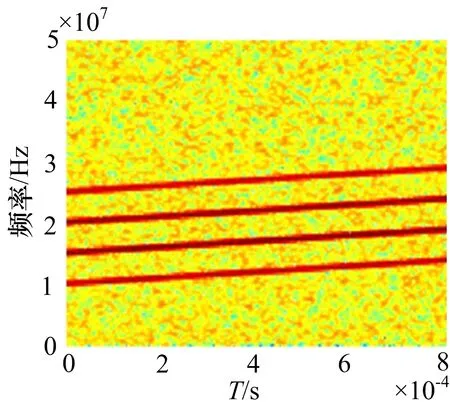
圖3 某路接收混合信號時頻分析圖

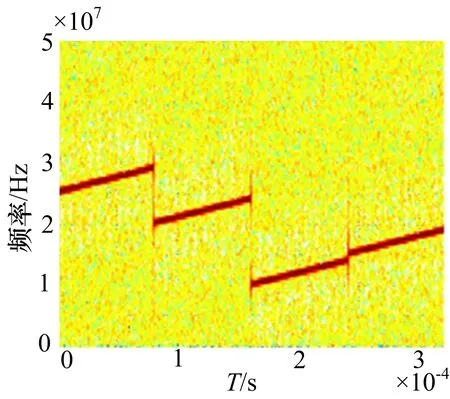
圖4 分離信號時頻分析圖

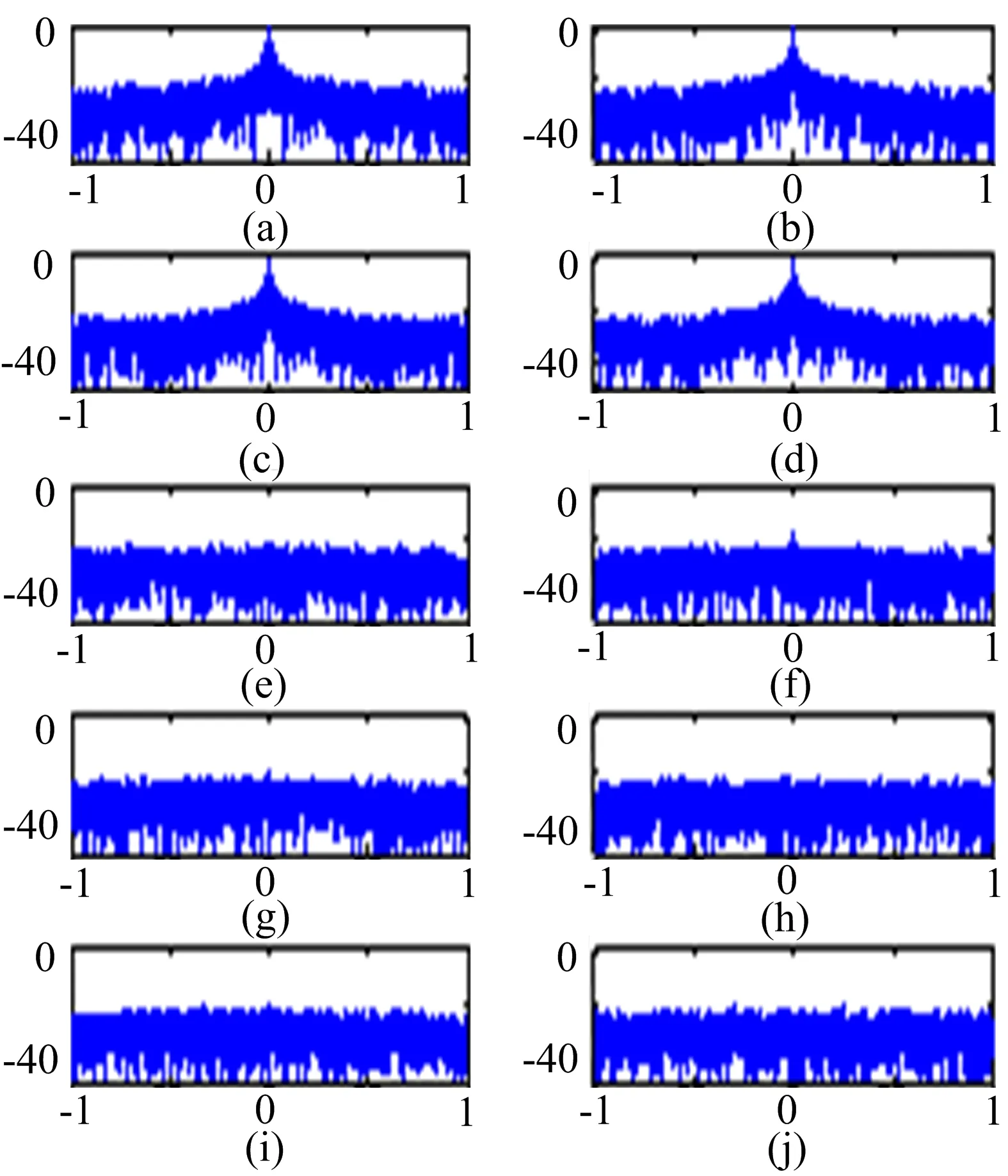
圖5分離信號的相關性

MIMO雷達通常在接收端利用收發聯合虛擬陣列的信號處理方式，并采用諸如MUSIC、ESPRIT等算法進行空間譜估計。根據本文提出的MIMO雷達對抗架構，對分離獲得的信號進行單獨的隨機相位調制，實現對MIMO雷達收發正交通道的干擾，即雷達接收端接收到的信號如式(7)所示，在發射導向性矢量中引入了相位干擾φm，經過MUSIC算法處理后，本應在-10°方向形成尖銳的譜峰，卻得到了雜亂無章的譜估計圖，如圖6所示。這就說明，本文提出的方法，能夠對MIMO雷達進行有效的角度干擾。

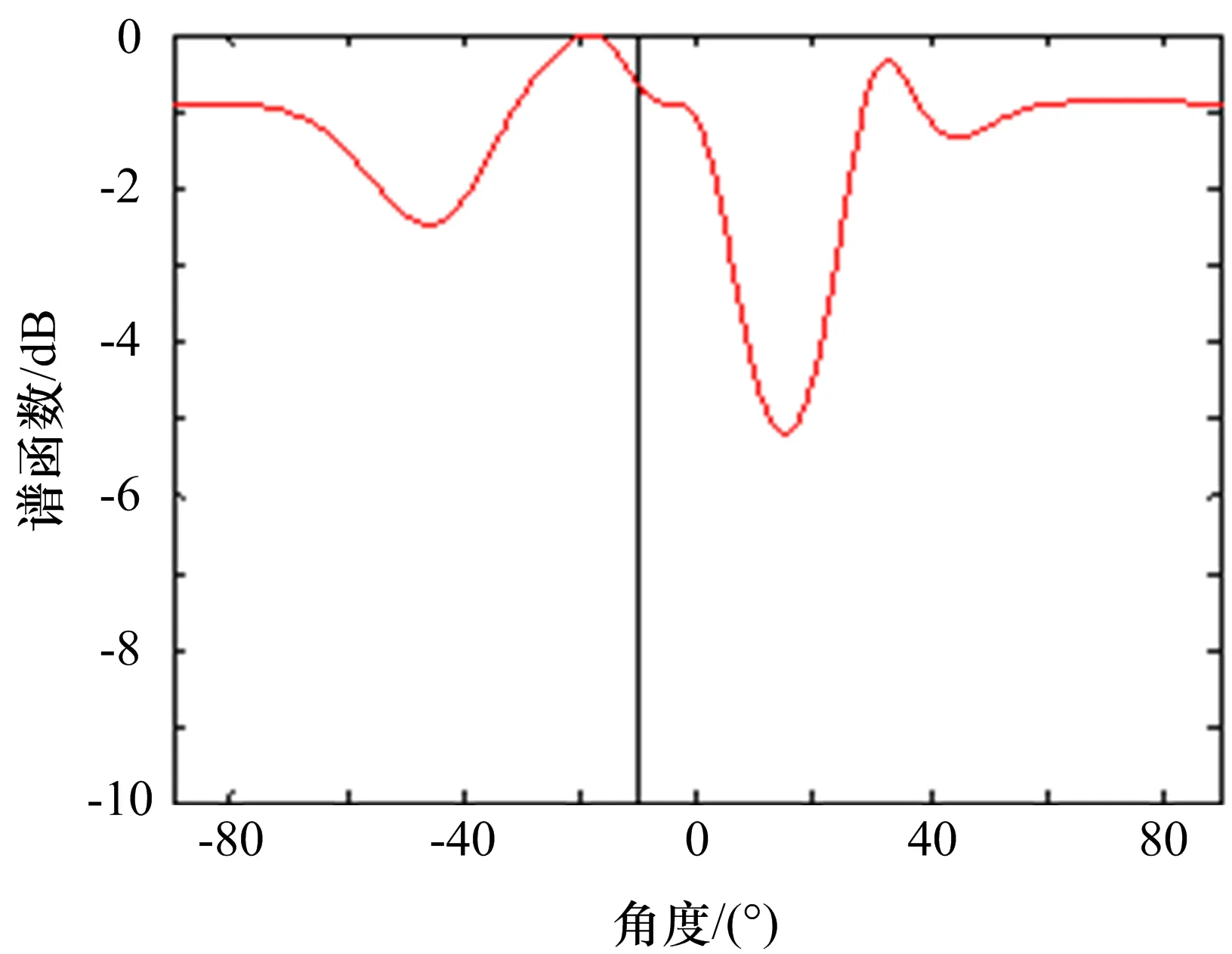
圖6 MIMO雷達接收端進行收發聯合譜估計結果

5 結束語

本文簡要分析了MIMO雷達與MIMO雷達偵察的信號模型，對比了其區別，提出了基于盲信號處理的MIMO雷達對抗系統模型，對MIMO雷達偵察與干擾方法進行了一定的分析，并給出了仿真結果。但是，針對噪聲背景下的混疊信號盲分離算法以及分布式對抗原理系統實現等問題，仍亟待后續深入研究。■

[1] Fishler E, Haimovich A, Blum R,et al.MIMO radar:an idea whose time has come[C]∥Proc.IEEE Radar Conf., 2004:71-78.

[2] Daum F, Huang J. MIMO radar: snake oil or good idea?[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(5)：8-12.

[3] Li J, Stoica P. MIMO radar with co-located antenna: review of some recent work[J]. IEEE Signal Processing Magazine, 2007,24:106-114.

[4] Haimovich M, Blum RS, Cimini LJ. MIMO radar with widely separated antennas[J].IEEE Signal Processing Magazine, 2008,25,:116-129.

[5] Hassan K, Nsiala Nzéza C, Gautier R ,et al.Blind Detection of the Number of Transmitting[C]∥11th International Conference on ITS Telecommunications Antennas for Spatially-Correlated MIMO Systems, 2011.

[6] 胡建華.面向MIMO系統的發射天線數目盲估計[D].西安:西安電子科技大學, 2013.

[7] 方健.基于盲源分離的MIMO雷達偵察與識別[D].西安:西安電子科技大學, 2014.

[8] 海韋里恩,卡爾胡恩. 獨立成分分析[M].北京：電子工業出版社，2014.

[9] 冷巨昕.盲信號處理中信源個數估計方法研究[D].成都：電子科技大學, 2009.