多模光力系統中的非傳統聲子阻塞?

石海泉 謝智強 徐勛衛 劉念華

1)(南昌大學材料科學與工程學院,南昌 330031)

2)(華東交通大學應用物理系,南昌 330013)

3)(南昌大學高等研究院,南昌 330031)

1 引 言

1997年,Imamo?lu等[1]在研究含克爾非線性介質腔中光子的統計性質時提出了光子阻塞概念,用以描述光子通過含有強克爾非線性介質光腔時表現出強反聚束的行為.光子阻塞效應的一項重要應用是可以用于實現理想的單光子源.自從2005年Birnbaum等[2]首次在腔QED系統中觀測到光子阻塞效應以來,人們已經在很多不同系統中觀測到光子阻塞[3?7].近年來,光力系統研究作為量子光學發展的新方向之一,引起了人們的廣泛關注[8?13].光力系統由光腔與機械振子通過光壓力作用耦合組成,既可以用于改變光場的性質,也可以用于控制機械振子的行為.已有較多的研究發現,在強光力耦合條件下光力系統中也可以出現光子阻塞效應[14?21],這為實現單光子源提供了一條新的途徑.

類比光子阻塞效應,聲子阻塞效應[22]可以作為實現單聲子源的機制之一.理論預言,當機械振子與二能級系統耦合時,在色散區[22?25]和共振區[26,27]都可以實現聲子阻塞效應.然而除少數文獻外[28?30],對于光力系統中聲子統計性質的專門研究還比較少,如何在光力系統中實現聲子阻塞還有待研究.多模光力系統作為光力系統的重要模型之一是目前研究的熱點之一.研究發現,多模光力系統中可以出現很多獨特的有趣現象,例如非線性作用增強[31,32]、高保真度量子態傳輸[33?35]、聲子激光[29,36,37]、邊帶不可分辨條件下的基態冷卻[38?41]、弱光力耦合條件下的光子阻塞[42]、超高分辨率質量傳感[43]等.

本文研究多模光力系統中聲子的統計性質,其中多模光力系統由一個機械模與兩個光學模組成.本文主要關注弱光力耦合條件下的聲子阻塞,類比非傳統光子阻塞效應[42,44?54],它也被稱為非傳統聲子阻塞[27].與傳統聲子阻塞源于強非線性作用的物理機制[22?26]不同,非傳統聲子阻塞的物理起源是因為干涉相消作用[45,46],導致雙聲子態的占居概率被抑制,從而使得在弱非線性條件下也能出現強反聚束現象.

2 多模光力系統理論模型

本文將要研究的多模光力系統由一個機械模和兩個光學模組成[29,31,32,36,37],如圖1所示,其哈密頓量可以表示為(?=1)

圖1 多模光力系統示意圖 機械模b同時與環形微腔中光學模aL和aR產生光力作用;光學模之間線性耦合,強度為J0;機械模和光學模都受到外加驅動場作用,強度為ε和?i(i=1,2),?表示驅動場間的相位差Fig.1.Schematic diagram of a multimode optomechanical system:The mechanical mode b is optomechanical coupled to the optical modes aLand aRsimultaneously;the optical modes are linearly coupled together with strength J0;the mechanical and optical modes are driven by external fields with strengths ε and ?i(i=1,2),and ? denotes the phase difference of the driving fields.

為了后續討論方便,對系統哈密頓量(1)式進行簡化.首先,將耦合光學模算符變換為對稱和反對稱模式,即做變換和可得

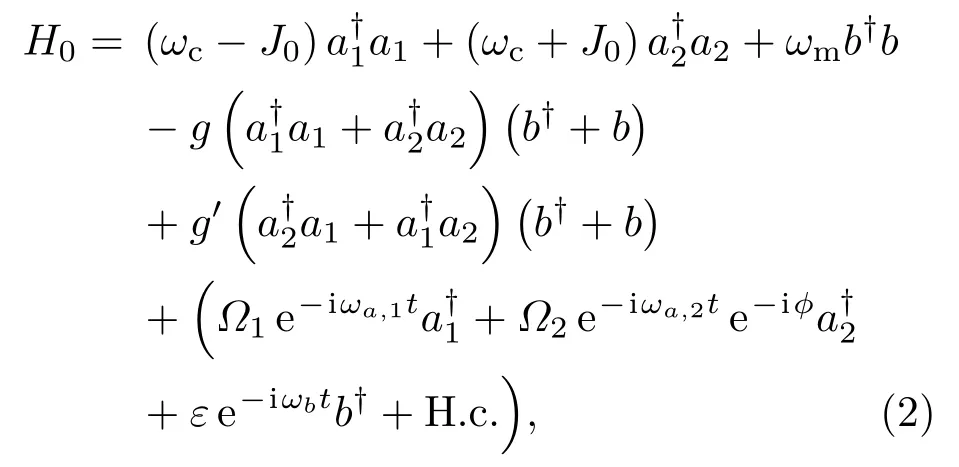
其中g≡(gL+gR)/2和g′≡(gR?gL)/2.接下來,對哈密頓量做變換,H′=UH0U?,其中

假設系統參數滿足弱光力耦合和邊帶可分辨條件g＜γc?ωm,以及共振條件和在旋轉波標架下其中R(t)=忽略高頻振蕩項和高階小量,系統的哈密頓量可以近似寫為

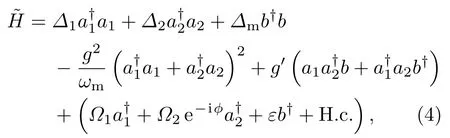
其中失諧量Δ1=ωc?J0?ωa,1,Δ2=ωc+J0?ωa,2,Δm=ωm?ωb.假設驅動場強度滿足不等式?1?γc＞{g,ε,?2,γm},這時光學模a1中的平均光子數很大,〈a1〉?1,光學模a2中的平均光子數很小,〈a2〉＜1,機械模中的平均聲子數也較小,〈b〉＜1.為了討論簡單,光學模a1可以作為經典場近似處理,即a1→〈a1〉;另外假設失諧量由此系統的哈密頓量可以進一步簡化為

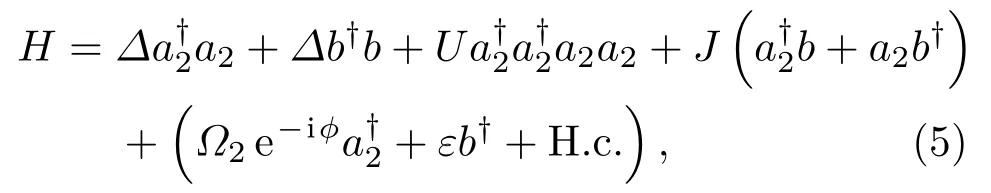
其中等效非線性作用強度U≡?g2/ωm,等效線性耦合強度J=g′〈a1〉.〈a1〉的相位可以通過改變外加驅動場的相位調節,不失一般性,本文假設J,?2和ε都為實數,不同驅動場之間的相位差用?表示.下面從哈密頓量(5)式出發,研究機械模中的聲子阻塞效應.

在穩態下(t→+∞),系統中聲子的統計性質可以由二階相關度來表征.聲子二階相關度的定義為

其中nb≡b?(t)b(t)為平均聲子數,平均聲子數和二階相關度都可以利用系統密度算符ρ計算得出.系統的密度算符ρ隨時間的演化行為滿足以下主方程[56]

其中nth為機械模中的平均熱聲子數.根據玻色-愛因斯坦統計可得nth=[exp(?ωm/kBT)?1]?1,其中kB為玻爾茲曼常數,T為機械振子所處環境的平衡溫度.由于光學模本征頻率較高,可以忽略環境中熱光子的影響.

3 聲子阻塞最優條件

本節討論觀測聲子阻塞的最佳條件.雖然系統哈密頓量(7)式從數學上看與文獻[50]中的類似,但是本文所選取的參數范圍與文獻[50]有所不同:光腔的衰減率遠大于機械振子的衰減率,即γc?γm.這一不同會導致聲子阻塞出現的最優條件與文獻[50]中給出的條件大不相同.所以有必要根據文獻[45]中給出的方法,重新推導聲子阻塞出現的最佳條件.

首先,假設系統狀態可以用下列波函數來描述

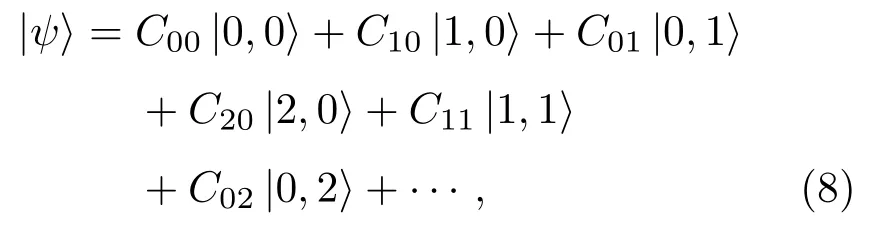
其中|n,m〉代表系統處于n個光子m個聲子的態,對應系數Cnm(n和m為非負整數)為其概率幅.由于驅動場強度?2和ε都較弱,平均光子數和聲子數都較少,聲子或者光子數越多的態出現的概率越小,可以近似認為:C00?{C10,C01}?{C20,C11,C02}?···.將波函數(8)式和哈密頓量(5)式代入薛定諤方程,id|ψ〉/dt=H|ψ〉,可得波函數中的系數Cnm滿足的動力學方程

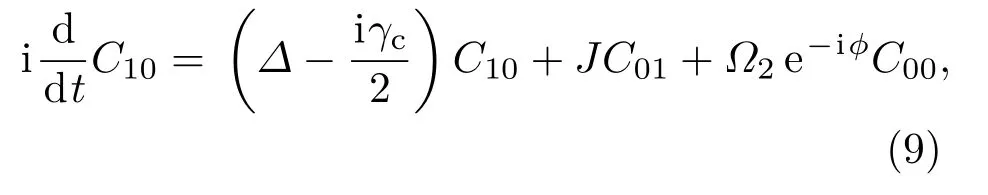
在穩態下,取dCnm/dt=0,于是系數Cnm滿足線性方程組

由(14)和(15)式解得

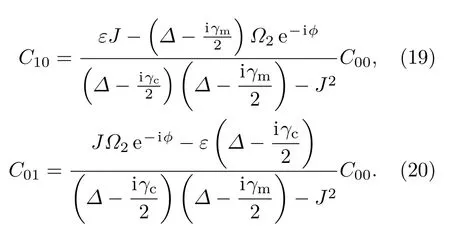
將其代入(16)—(18)式中,并利用聲子阻塞出現的條件,即C02=0,可得系數C20,C11,C00滿足線性方程組

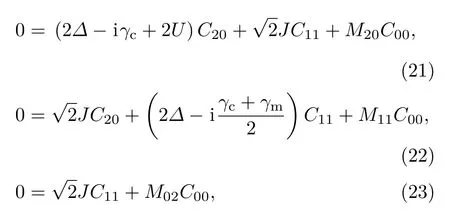
其中

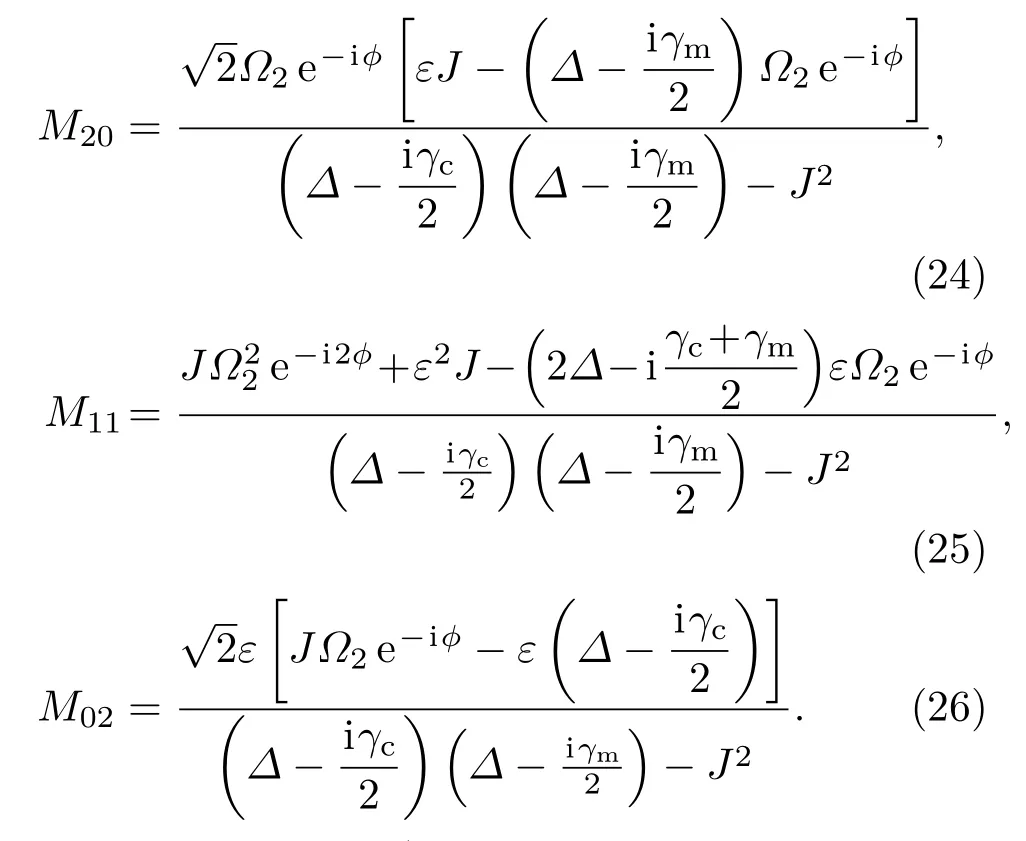
上述方程組(21)—(23)式有非零解的充要條件是其系數矩陣行列式為零.

當光學模a2不受外加驅動場作用,即?2ei?=0時,由方程組(21)—(23)式系數矩陣行列式實部和虛部分別為零可得

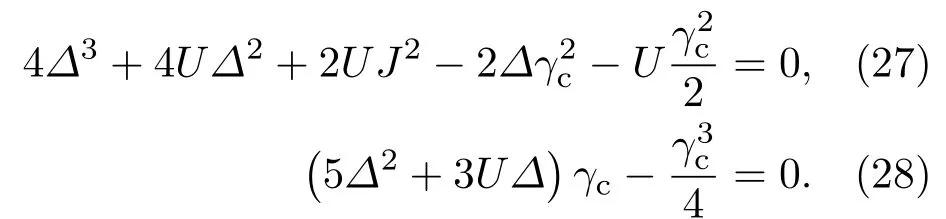
由此推導出聲子阻塞效應的最佳失諧量和光力耦合強度分別為

當等效線性耦合強度遠大于光腔的衰減率,即J?γc/2時,(29)和(30)式簡化為

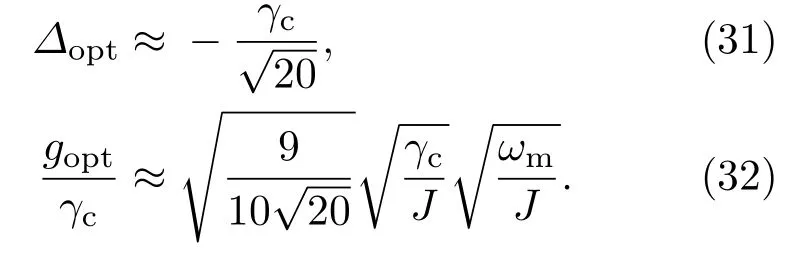
當光學模a2受到外加驅動場作用,即?2ei?/=0時,定義強度比值η=ε/?2.由方程組(21)—(23)式系數矩陣行列式為零可得

當?=0時,上式中的實部和虛部分別為零可得

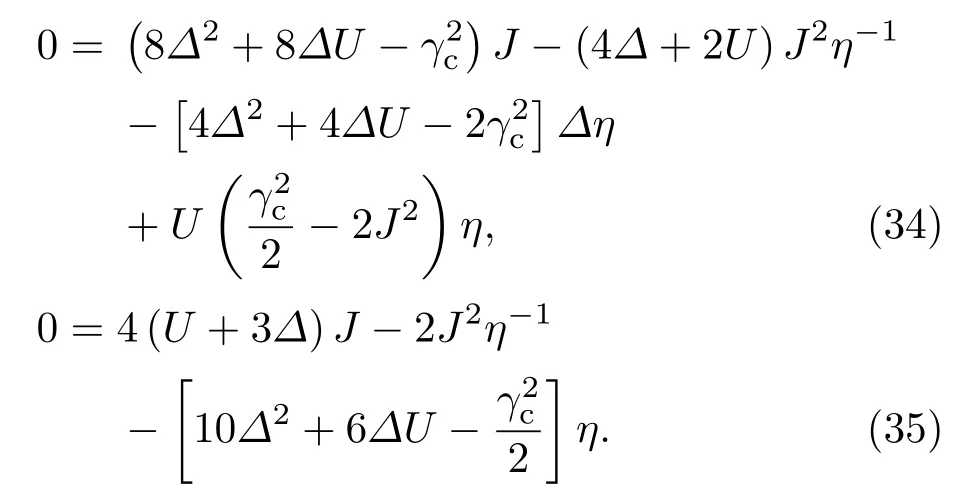
由此推導可得,觀測聲子阻塞效應的最佳失諧量滿足以下方程

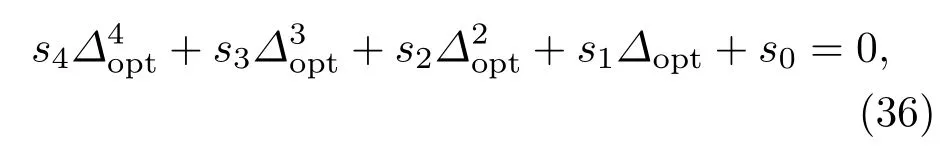
其中系數si(i=0,1,2,3,4)分別定義為

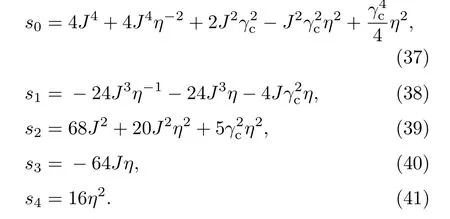
另外,觀測聲子阻塞效應的最佳非線性強度和最佳光力耦合強度由下式給出:

其中為了保證gopt為實數,Uopt的取值必須小于零.通過(36)—(42)式可以看出,觀測聲子阻塞效應的最佳失諧量和非線性強度都與驅動強度比值η有關.換言之，我們可以通過改變驅動強度比值η調節聲子阻塞現象出現的條件,該性質可以用于實現可調單聲子源.

4 數值結果與分析

本節數值求解主方程得到密度矩陣ρ,然后通過繪圖研究聲子二階相干度隨系統參數的變化趨勢.

4.1 非傳統聲子阻塞

首先,討論光學模a2不受外加驅動場作用,即?2ei?=0時,聲子的統計性質.圖2(a)中給出了聲子二階相干度log10[g(2)b(0)]隨失諧量Δ/γc和光力耦合強度g/γc變化的等高線圖,圖2(b)和圖2(c)中分別給出了log10[g(2)b(0)]隨失諧量Δ/γc和光力耦合強度g/γc的變化曲線,可以看出聲子阻塞出現的最佳失諧量為Δ≈?0.217γc,最佳光力耦合強度為g≈0.819γc,這與(29)—(32)式預言的最佳條件符合.圖2(d)中給出了隨時間延遲τ/(2π/J)變化曲線.隨時間延遲τ出現振蕩行為,振蕩周期為2π/J.該振蕩行為是由于粒子在光學模與機械模之間躍遷導致的.振蕩幅度隨著時間延遲τ/(2π/J)延長逐漸衰減,衰減速率與光學模的衰減率為同一量級.

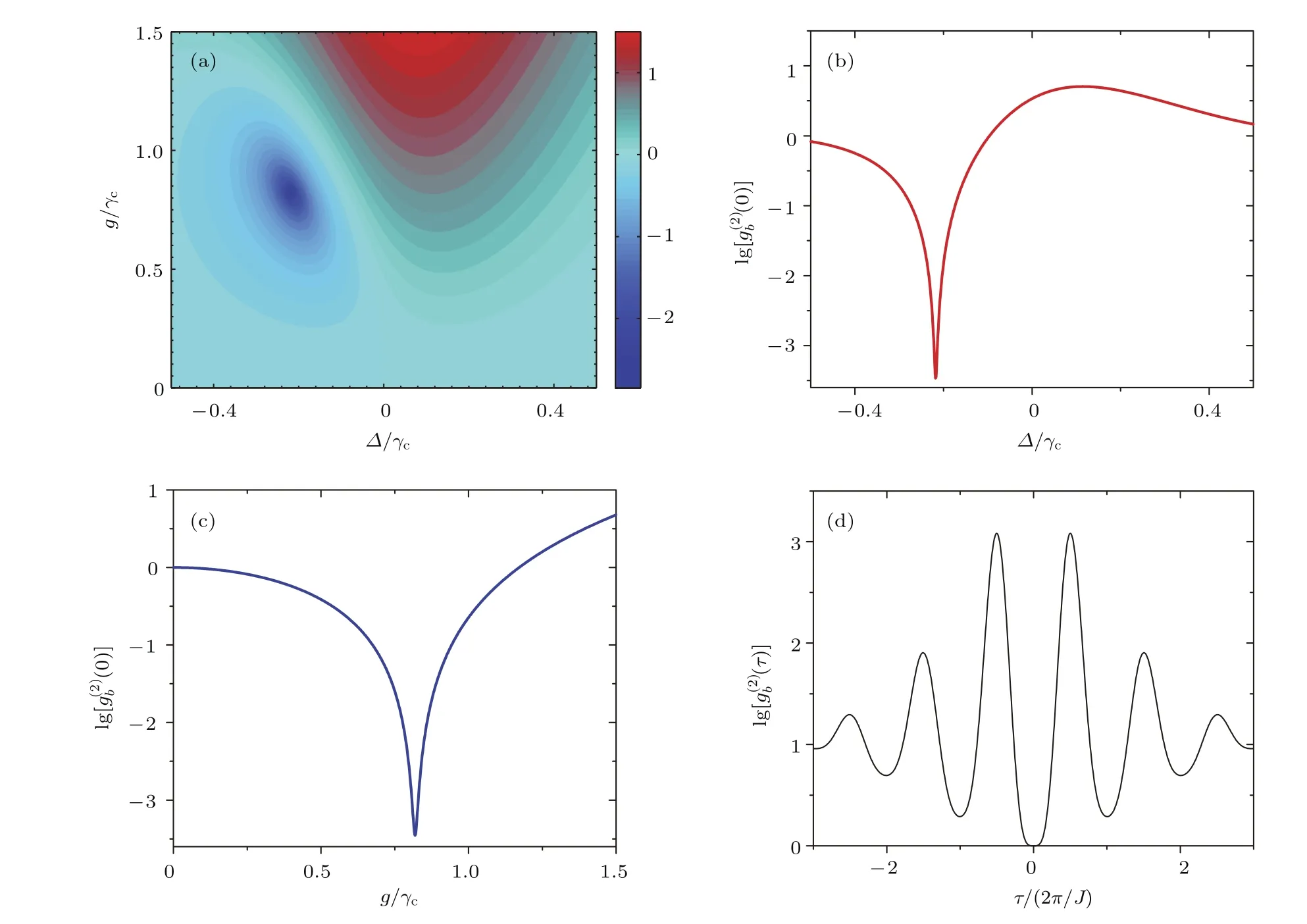
圖2 (a)聲子二階相干度隨失諧量Δ/γc和光力耦合強度g/γc變化的等高線圖;(b)log10[gb(2 )(0)]隨失諧量Δ/γc的變化曲線,g=0.819γc[取值由(30)式計算得出];(c)log10[gb(2 )(0)]隨光力耦合強度g/γc的變化曲線,Δ=?0.217γc[取值由(29)式計算得出];(d)gb(2 )(τ)隨時間延遲τ/(2π/J)變化曲線,Δ = ?0.217γc和g=0.819γc;其他參數為J=3γc,ωm=30γc,γm=0.01γc,ε=0.1γc,?2ei? =0,nth=0Fig.2.(a)Contour plot of the second-order correlation functions log10[gb(2)(0)]vs detuning Δ/γcand optomechanical coupling strength g/γc;(b)log10[gb(2)(0)]vs detuning Δ/γcwith g=0.819γcgiven by Eq.(30);(c)log10[gb(2 )(0)]vs optomechanical coupling strength g/γcwith Δ = ?0.217γcgiven by Eq.(29);(d)gb(2 )(τ)vs time delay τ/(2π/J)with Δ = ?0.217γcand g=0.819γc.The other parameters are J=3γc, ωm=30γc, γm=0.01γc, ε =0.1γc,?2ei? =0,nth=0.

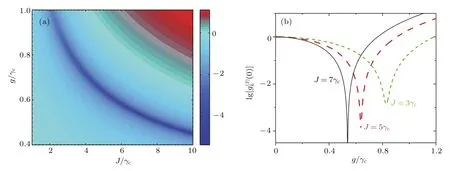
圖3 (a)隨線性耦合強度J/γc和光力耦合強度g/γc變化的等高線圖;(b)隨光力耦合強度g/γc的變化曲線;其中其他參數與圖2一致Fig.3.(a)Contour plot of>vs linear coupling strengthand optomechanical coupling strength g/γc;(b)vs optomechanical strength g/γc.Here=10J and the other parameters are the same as in Fig.2.

4.2 可調聲子阻塞

本小節研究外加驅動場作用于光學模a2,即?2ei?/=0時,聲子的統計性質隨外加驅動場間強度的比值和相位差的變化行為.通過數值求解方程(36)—(42)式,圖4(a)中給出了最佳光力耦合強度gopt/γc和最佳失諧量Δopt/γc隨驅動場強度比值η的變化曲線.從圖中可以看出,最佳光力耦合強度gopt/γc和最佳失諧量Δopt/γc隨驅動場強度比值η變化而變化.另外,當η＞4.65時,gopt＜γc,這為在弱光力耦合條件下實現聲子阻塞提供了有利條件.圖4(b)中給出了隨驅動場強度比值η和失諧量Δ/γc變化的等高線圖,其中紅色虛線由(36)式給出.由此可以看出,聲子反聚束現象出現的條件(深藍色區域)與(36)式給出的最佳失諧量(紅色虛線)符合得很好.

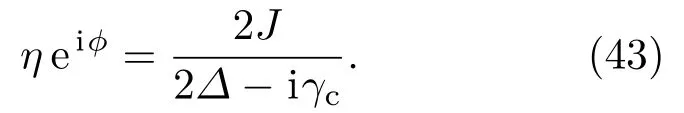
圖4 (a)gopt/γc[(42)式]與Δopt/γc[(36)式]隨驅動場強度比值η的變化曲線;(b)log10[g(2)b (0)]隨驅動場強度比值η和失諧量Δ/γc變化的等高線圖;其他參數取值與圖2一致Fig.4. (a) Δopt/γc[from Eq.(36)]and gopt/γc[from Eq.(42)]vs the strength ratio η;(b)contour plot of log10[g(2)b(0)]vs the strength ratio η and detuning Δ/γc.The other parameters are the same as in Fig.2.

圖5 (a)和(b)隨相位差?/π和驅動場強度比值η變化等高線圖;(c)log10[gb(2 )(0)]隨驅動場強度比值η變化曲線,其中?=0.634π;(d)log10[gb(2 )(0)]隨相位差?/π變化曲線,其中η=6;(a)和(c)中,Δ 和g的取值由(29)和(30)式計算得出;(b)和(d)中,Δ和g的取值由(36)—(42)式計算得出,其他參數取值與圖2一致Fig.5.(a)and(b)Contour plot of vs the phase difference ?/π and strength ratio η;(c)log10[gb(2 )(0)]vs the strength ratio η with ? =0.634π;(d)log10[gb(2 )(0)]vs the phase difference ?/π with η =6.(a)and(c) Δ and g are given by Eqs.(29)and(30);(b)and(d) Δ and g are given by Eqs.(36)–(42).The other parameters are the same as in Fig.2.

將圖5(a)和圖5(c)中參數代入上式可得,η≈5.5和?≈0.634π,這與圖中聚束效應出現的條件一致.

4.3 環境中熱聲子的影響

與光子阻塞不同,由于聲子的頻率較低,聲子阻塞和隧穿現象容易受到環境中熱聲子的影響.圖6(a)和圖6(b)中給出了隨平均熱聲子數nth和機械驅動強度ε/γc變化等高線圖;圖6(c)和圖6(d)中給出了不同熱聲子條件下隨機械驅動強度ε/γc變化曲線.圖6(a)和圖6(c)中選取了圖5(a)中聲子阻塞出現的最優參數η ≈2.764和? ≈0.634π;圖6(b)和圖6(d)中選取了圖5(a)中聲子隧穿出現的最優參數η≈5.5和?≈0.634π.從圖中可以看出,當考慮環境熱聲子影響時,適當提高驅動強度ε/γc利于觀測聲子阻塞效應;隨著環境中熱聲子數的增加,觀測聲子阻塞和隧穿現象需要的機械驅動強度ε/γc逐漸增強.另外,隨著環境中熱聲子數的增加,log10[g(2)b(0)]的最小值逐漸增大(或者最大值逐漸減小),即聲子阻塞(隧穿)效應越來越弱.

5 結 論

本文研究了多模光力系統中的聲子阻塞效應,給出了聲子阻塞出現的最佳條件.研究發現,聲子阻塞效應在弱光力耦合條件下也能出現,而且出現聲子阻塞效應所需要的最佳光力耦合強度可以通過外加驅動場來調節.另外,我們還研究了多驅動條件下,驅動場間的強度比值和相位差對聲子阻塞效應的影響.發現通過調節驅動場強度比值或者相位差,可以觀測到機械模中的聲子在反聚束和聚束之間轉換.這為實現可調單聲子源提供了一個備選方案.最后,討論了環境中熱聲子對聲子阻塞效應的影響,發現熱聲子對聲子阻塞效應有破壞作用.為了觀測聲子阻塞效應,必須克服環境中熱聲子的影響,例如降低環境的溫度,或者通過其他方法降低機械振子的有效溫度,提高機械振子的共振頻率.近年來,光力系統中已經制備出了吉赫茲量級的高頻機械振子[57,58],這為實現聲子阻塞效應提供了有利條件.

圖6 (a)和(b)log10[g(2)b (0)]隨平均熱聲子數nth和機械驅動強度ε/γc變化等高線圖;(c)和(d)log10[g(2)b (0)]隨機械驅動強度ε/γc變化曲線;(a)和(c)中選取η≈2.764;(b)和(d)中選取η≈5.5;其他參數與圖5(c)一致Fig.6.(a)and(b)Contour plot of log10[g(2)b (0)]vs mean thermal phonon number nthand mechanical driving strength ε/γc;(c)and(d)log10[g(2)b(0)]vs mechanical driving strength ε/γc. η≈ 2.764 in(a)and(c);η≈ 5.5 in(b)and(d).The other parameters are the same as in Fig.5(c).

[1]Imamo?lu A,Schmidt H,Woods G,Deutsch M 1997Phys.Rev.Lett.79 1467

[2]Birnbaum K M,Boca A,Miller R,Boozer A D,Northup T E,Kimble H J 2005Nature436 87

[3]Dayan B,Parkins A S,Aoki T,Ostby E P,Vahala K J,Kimble H J 2008Science319 1062

[4]Dubin F,Russo C,Barros H G,Stute A,Becher C,Schmidt P O,Blatt R 2010Nature Phys.6 350

[5]Faraon A,Fushman I,Englund D,Stoltz N,PetroffP,Vu?kovi? J 2008Nature Phys.4 859

[6]Lang C,Bozyigit D,Eichler C,Steffen L,Fink J M,Abdumalikov Jr A A,Baur M,Filipp S,da Silva M P,Blais A,WallraffA 2011Phys.Rev.Lett.106 243601

[7]Hoffman A J,Srinivasan S J,Schmidt S,Spietz L,Aumentado J,Türeci H E,Houck A A 2011Phys.Rev.Lett.107 053602

[8]Aspelmeyer M,Kippenberg T J,Marquardt F 2014Rev.Mod.Phys.86 1391

[9]Liu Y C,Hu Y W,Wong C W,Xiao Y F 2013Chin.Phys.B22 114213

[10]Chen X,Liu X W,Zhang K Y,Yuan C H,Zhang W P 2015Acta Phys.Sin.64 164211(in Chinese)[陳雪, 劉曉威,張可燁,袁春華,張衛平2015物理學報64 164211]

[11]Chen H J,Mi X W 2011Acta Phys.Sin.60 124206(in Chinese)[陳華俊,米賢武 2011物理學報 60 124206]

[12]Zhang D,Zheng Q 2013Chin.Phys.Lett.30 024213

[13]Jiang C,Cui Y,Li X 2016Chin.Phys.B25 54204

[14]Rabl P 2011Phys.Rev.Lett.107 063601

[15]Qiu L,Gan L,Ding W,Li Z Y 2013J.Opt.Soc.Am.B30 1683

[16]Xu X W,Li Y J,Liu Y X 2013Phys.Rev.A87 025803[17]Liao J Q,Law C K 2013Phys.Rev.A87 043809

[18]Liao J Q,Nori F 2013Phys.Rev.A88 023853

[19]Hu D,Huang S Y,Liao J Q,Tian L,Goan H S 2015Phys.Rev.A91 013812

[20]Lü X Y,Wu Y,Johansson J R,Jing H,Zhang J,Nori F 2015Phys.Rev.Lett.114 093602

[21]Xie H,Lin G W,Chen X,Chen Z H,Lin X M 2016Phys.Rev.A93 063860

[22]Liu Y X,Miranowicz A,Gao Y B,Bajer J,Sun C P,Nori F 2010Phys.Rev.A82 032101

[23]Didier N,Pugnetti S,Blanter Y M,Fazio R 2011Phys.Rev.B84 054503

[24]Miranowicz A,Bajer J,Lambert N,Liu Y X,Nori F 2016Phys.Rev.A93 013808

[25]Wang X,Miranowicz A,Li H R,Nori F 2016Phys.Rev.A93 063861

[26]Ramos T,Sudhir V,Stannigel K,Zoller P,Kippenberg T J 2013Phys.Rev.Lett.110 193602

[27]Xu X W,Chen A X,Liu Y X 2016Phys.Rev.A94 063853

[28]Nunnenkamp A,B?rkje K,Girvin S M 2011Phys.Rev.Lett.107 063602

[29]L?rch N,Hammerer K 2015Phys.Rev.A91 061803

[30]Seok H,Wright E M 2017Phys.Rev.A95 053844

[31]Ludwig M,Safavi-Naeini A H,Painter O,Marquardt F 2012Phys.Rev.Lett.109 063601

[32]Stannigel K,Komar P,Habraken S J M,Bennett S D,Lukin M D,Zoller P,Rabl P 2012Phys.Rev.Lett.109 013603

[33]Wang Y D,Clerk A A 2012Phys.Rev.Lett.108 153603

[34]Tian L 2012Phys.Rev.Lett.108 153604

[35]Li H K,Ren X X,Liu Y C,Xiao Y F 2013Phys.Rev.A88 053850

[36]Grudinin I S,Lee H,Painter O,Vahala K J 2010Phys.Rev.Lett.104 083901

[37]Wang H,Wang Z X,Zhang J,?zdemir S K,Yang L,Liu Y X 2014Phys.Rev.A90 053814

[38]Gu W J,Li G X 2013Phys.Rev.A87 025804

[39]Ojanen T,B?rkje K 2014Phys.Rev.A90 013824

[40]Guo Y J,Li K,Nie W J,Li Y 2014Phys.Rev.A90 053841

[41]Liu Y C,Xiao Y F,Luan X S,Gong Q H,Wong C W 2015Phys.Rev.A91 033818

[42]Xu X W,Li Y J 2013J.Opt.B:At.Mol.Opt.Phys.46 035502

[43]Chen H J,Fang X W,Chen C Z,Li Y 2016Acta Phys.Sin.65 194205(in Chinese)[陳華俊,方賢文,陳昌兆,李洋2016物理學報65 194205]

[44]Liew T C H,Savona V 2010Phys.Rev.Lett.104 183601

[45]Bamba M,Imamoglu A,Carusotto I,Ciuti C 2011Phys.Rev.A83 021802

[46]Lemonde M A,Didier N,Clerk A A 2014Phys.Rev.A90 063824

[47]Gerace D,Savona V 2014Phys.Rev.A89 031803

[48]Kyriienko O,Shelykh I A,Liew T C H 2014Phys.Rev.A90 033807

[49]Xu X W,Li Y 2014Phys.Rev.A90 033809

[50]Xu X W,Li Y 2014Phys.Rev.A90 043822

[51]Kyriienko O,Liew T C H 2014Phys.Rev.A90 063805

[52]Shen H Z,Zhou Y H,Yi X X 2015Phys.Rev.A91 063808

[53]Zhou Y H,Shen H Z,Yi X X 2015Phys.Rev.A92 023838

[54]Tang J,Geng W,Xu X 2015Sci.Rep.5 9252

[55]Anetsberger G,Arcizet O,Unterreithmeier Q P,Riviere R,Schliesser A,Weig E M,Kotthaus J P,Kippenberg T J 2009Nature Phys.5 909

[56]Carmichael H J 1993An Open Systems Approach to Quantum Optics(Lecture Notes in Physics vol.18)(Berlin:Springer)pp9–13

[57]Fang K,Matheny M M,Luan X,Painter O 2016Nature Photon.10 489

[58]Han X,Zou C,Tang H 2016Phys.Rev.Lett.117 123603