五軸轉向車輛輸出反饋魯棒穩定控制系統設計＊

滿緒民 王吉華 李超 梁鵬云 郭棟

（山東理工大學，淄博 255049）

1 前言

隨著社會與經濟的不斷發展，人們對大功率車輛載重能力的要求越來越高，考慮到國家標準對車輛外廓尺寸、質量及軸載的限制，一味地提高每個軸的載重能力，或者降低整車質量已經沒有較明顯的作用，針對這種情況，增加車軸數量的方法被提出，多軸汽車隨之出現[1]。

迄今為止，國內在多軸轉向控制策略方面進展較為迅速。王吉華研制了遙控駕駛四軸轉向模型車半物理仿真試驗系統，建立了車輛模型和控制算法的仿真試驗驗證平臺[2]；龐文杰證明了CMAC-PID控制的多軸轉向系統有較高的響應精度和較快的響應速度[3]；葉俊等利用粒子群算法設計了H∞魯棒控制器[4]；王菁通過仿真試驗驗證了約束H∞控制方法可以有效提高4WS汽車的操縱穩定性，基于干擾觀測器（DOBC）控制的4WS汽車都可以保持汽車的穩定性并降低駕駛員的操縱難度[5]；高峰著重介紹了某五軸雙前軸轉向重型汽車的建模過程[6]；黃麗杰討論了不確定模糊時滯系統的魯棒性能分析和控制器設計問題[7]。這些控制算法也可應用到控制多軸車輛轉向[8-9]中去。

本文根據五軸車輛在行駛中受到路面狀況、質心高度等參數影響的特點設計了輸出反饋魯棒穩定控制系統。對該系統進行仿真分析表明，五軸轉向車輛在行駛過程中可適應參數的變化，從而達到轉向穩定。

2 五軸轉向汽車二自由度模型

假定在驅動力不大的情況下，不計空氣阻力、載荷的變化，忽略地面切向力對輪胎側偏特性影響效果的前提下，將實際五軸轉向汽車簡化為單側的五輪模型。其線性二自由度模型如圖1所示，樣車部分參數如表1所示。

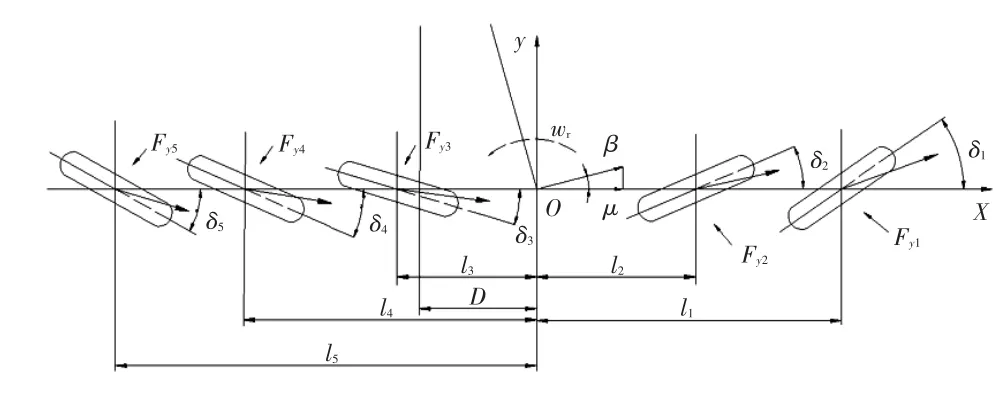
圖1 五軸轉向汽車二自由度模型

表1 五軸汽車部分參數

根據五軸轉向汽車運動參數關系式[10]，推導出二自由度運動微分方程：

式中，β為質心側偏角；u為質心前進速度；ωr為橫擺角速度；δi為第i軸轉向輪轉角；v為質心速度。

把多軸車輛動力學模型簡化為線性二自由度汽車模型，狀態變量x=[βωr]T，輸入變量u=[δ1δ2δ3δ4δ5]，輸出變量為y，A、B、C為系數矩陣，其狀態空間表達式為：

各軸等效轉角與前軸轉角的比例系數定義為Ki：

3 具有參數不確定性的魯棒穩定控制系統設計

3.1 閉環控制系統描述

考慮如下具有參數不確定的多變量系統[11]：

設系統（A、B、C、D）完全可控、可觀，且系統的參數不確定為范數有界，記

取動態反饋控制器構成如圖2所示的閉環系統，動態反饋控制器的方程為：

式中，Ar、Br、Kx、Kr為所設計的動態狀態反饋控制器的系數矩陣；Y為該控制器的輸入變量；xr為該控制器的狀態變量；h為該控制器的輸出變量。

圖2 具有參數不確定的閉環系統

設計控制器（Ar、Br、Kx、Kr）的目的是使閉環系統穩定，稱此控制器為魯棒穩定控制器，同時稱該系統為魯棒穩定控制系統[9]。根據圖2和式（4）、式（6），可得閉環系統的動態方程，即

3.2 魯棒穩定性控制器設計原理

式中，α為區間系統的魯棒穩定度；m0為可取小于1的常數；為狀態空間中的狀態轉移矩陣，(t-τ)為時間的偏差。

根據式（5）～式（7）可得：

將式（8）和（10）代入式（9），可得：

根據Bellman-Gronwall引理將式（12）可整理得：

根據式（5）、式（9）、式（11）得：

由式（7）和式（14）、式（15）可知，如果閉環系統是魯棒漸進穩定的，所設計的動態狀態反饋控制器（Ar、Br、Kx、Kr）要滿足[9]：

式中，Re表示取復數的實部。

3.3 樣車魯棒控制器設計

針對五軸轉向樣車，以第1軸轉向角度為輸入，采用高速（80km/h）工況進行轉向穩定性分析，五軸重型樣車的部分參數值如表1所示。

按照圖2來設計魯棒控制器，然后根據式（6），針對其不確定性確定控制器參數，通過MATLAB編程計算得到式（7）中矩陣Apr的特征值，如果控制器滿足式（15），該條件下的閉環系統一定是魯棒漸進穩定的。將A、B、C各矩陣代入式（2）得：

設該線性可變的有界函數為sin(x)，假定該系統經非線性參數攝動后的動態方程為：

按圖2設計魯棒控制器，使攝動系統穩定。根據式（10），有，即βA=1.5，βB=0.2，βC=0，βD=0。下面依次取不確定參數情況1、2、3下的動態控制器，判斷所設計的動態狀態反饋控制器（Ar、Br、Kx、Kr）是否滿足式（15），如滿足則可以使控制系統達到較穩定狀態。

a. 取不確定參數情況1控制器，令Kx=[-11]，Kr=[10]，可得：

根據式（7）可得閉環系統為：

通過MATLAB編程可求得式（19）中矩陣Apr的特征值分別為-7.0000、-2.5469+6.8375i、-2.5469-6.8375i、-3.3730。即得式（8）中的α=2.5469。

b. 取不確定參數情況2控制器，Kx=[1-2]，Kr=[-10]，可得特征值-7.0000、-0.3439+2.8755i、-0.3439-2.8755i、-7.8668。

因ρA=1.9；Reλ(Apr)＜0；α=0.3439，ρA與0.3439/m0的大小不確定，故不確定參數情況2控制器系統穩定性不確定。

c. 取不確定參數情況3控制器，再令Kx=[-22]，Kr=[10]，可得特征值為-3.0000、-2.2673+7.1885i、-2.2673-7.1885i、0.0677。因其中一個特征值的實部大于零，故不確定參數情況3控制器系統不穩定。

4 閉環控制系統仿真

首先，根據能使攝動系統穩定所滿足的條件，對該系統進行MATLAB參數計算來設計魯棒控制器，然后分別建立樣車的仿真模型，閉環控制系統的仿真模型和加入前輪轉角輸入的控制系統的仿真模型，進行Simulink仿真調試，得到并分析各個控制器的輸出變量波形，實現了動態控制器對攝動系統的穩定。

4.1 樣車開環仿真

據式（19）可建立樣車MATLAB/Simulink仿真模型，將第1軸轉向輪的轉角即前輪轉角10°作為輸入量，將橫擺角速度和質心側偏角作為輸出量，其仿真結果如圖3所示。

由圖3可知，初始時刻輸出變量橫擺角速度和質心側偏角響應值均為0，隨著仿真時間的增加，加入前輪轉角10°后，兩者的階躍響應值均有明顯變化，橫擺角速度趨于1.25(°)/s，質心側偏角趨于1.08°，系統穩定，但操縱穩定性較差。

4.2 不確定參數情況1、2閉環控制系統仿真

將樣車模型作為一個子系統，建立閉環控制系統仿真模型，并帶入前2組設計的控制器得到不確定參數情況1、2閉環控制系統模型的仿真波形如圖4所示。

圖3 輸出變量y=ωr和y=β的波形

圖4 不確定參數情況1、2的仿真波形

由圖4可知，在沒有控制時，初始時輸出變量橫擺角速度趨于1.25(°)/s，輸出變量質心側偏角趨于1.08°，隨著仿真時間的增加，經過控制后，橫擺角速度的響應值趨于0.1(°)/s，質心側偏角的響應值趨于0.13°，控制系統魯棒穩定且具有操縱穩定性。在t=0.2s時，不確定參數情況2控制系統輸出反饋量極為不穩定，因此，不確定參數情況1控制器最優化。

4.3 加入前輪轉角輸入的不確定參數情況1控制系統的仿真

為了進一步驗證本文的控制算法，樣車在不確定參數情況1下，對于圖4a中的樣車閉環控制響應1s時，在前輪已偏轉10°的基礎上繼續偏轉7°，進行閉環控制系統仿真，其仿真結果波形如圖5所示。

圖5 6秒過程的輸出波形

由圖5可知，初始時輸出變量橫擺角速度和質心側偏角初始值分別在1(°)/s和1°附近，在t=1s時，加入前輪轉角輸入時，橫擺角速度和質心側偏角波形瞬間均發生跳動，隨后兩者響應波形均逐漸趨于穩定。在t=3s時，橫擺角速度的響應值趨于0.4(°)/s，質心側偏角的響應值趨于0.06°，經仿真驗證了不確定參數情況1閉環控制系統的控制器設計可行，系統在3秒時得到了穩定控制而且具有較好的操縱穩定性。

5 結束語

本文首先建立了五軸轉向二自由度汽車模型，將汽車模型的微分方程轉化為狀態空間進行描述，由輸入和輸出建立出具有參數不確定性的魯棒穩定閉環控制系統，并對該系統進行MATLAB/Simulink仿真分析，設計的控制系統在五軸轉向過程中，魯棒適應參數的變化，達到轉向穩定。

[1]張小江，高秀華，趙建國，等.多軸轉向車輛零質心側偏角控制策略研究[J].農業裝備與車輛工程，2008（6）：13-15.

[2]王吉華.多軸轉向車輛狀態估計與控制研究[D].南京：南京航空航天大學，2013.

[3]龐文杰，王云超，葉存達，等.多軸車輛轉向系統神經網絡控制算法研究[J].計算機仿真，2015（6）：172-176.

[4]葉俊，黃勇，閆杰.基于粒子群算法的H∞魯棒控制器設計研究[J].科學技術與工程，2012，12（14）：3411-3414.

[5]王菁.線控四輪轉向汽車的魯棒控制研究[D].長春：吉林大學，2016.

[6]高峰.多軸汽車的操縱穩定性研究及轉向機構優化[D].錦州：遼寧工業大學，2015.

[7]黃麗杰.基于T-S模糊模型的時變時滯系統的魯棒控制研究[D].大慶：東北石油大學，2015.

[8] Watanabe K， Yama kawa J， Tanaka M， et al. Turningcharacteristics of Multi- axle vehicles[J]. Journal of TerraMechanics，2007，44（1）：81-87.

[9] Huh K， Kim J， Hong J. Handling and driving characteristicsfor six wheel vehicles[J]. Journal of Automobile Engineering，2000，214（2）：159-170.

[10]王吉華，魏民祥，杜言利，等.基于T-S模糊模型的多軸轉向車輛H∞魯棒控制[J].交通運輸工程學報，2012，12（4）：42-49.

[11]姜長生，吳慶憲，陳文華，等.現代魯棒控制基礎[M].哈爾濱：哈爾濱工業大學出版社，2005.