模糊數(shù)學(xué)在醫(yī)療診斷中的應(yīng)用

龔加安

（商洛職業(yè)技術(shù)學(xué)院，陜西 商洛 726000）

1965年，美國加州大學(xué) Berkely分校的著名控制論專家L.A.Zadeh教授提出了Fuzzy集的概念，從此有一大批數(shù)學(xué)工作者，工程師和數(shù)學(xué)家加入到了開發(fā)Fuzzy理論的行列之中，如今的Fuzzy理論已發(fā)展成包括Fuzzy邏輯等眾多的龐大理論體系，而且在應(yīng)用上也取得了很大的成功。本文主要從模糊數(shù)學(xué)在醫(yī)學(xué)中的應(yīng)用進(jìn)行研究。

怎樣用Fuzzy集表示高血脂概念當(dāng)然要靠名醫(yī)的臨床經(jīng)驗。名醫(yī)有著豐富的醫(yī)學(xué)經(jīng)驗，而這些經(jīng)驗大多數(shù)是模糊概念，如醫(yī)生常說某人有“血氣兩虧”“完谷不化”“舌苔薄黃”“脈象沉緩”等癥狀。這些模糊概念只有用隸屬函數(shù)才能演算，用隸屬度才能刻劃。因此，模糊邏輯可以而且能夠應(yīng)用與醫(yī)療診斷。研制“電腦醫(yī)生”要用它，醫(yī)療實踐也要用它。

下邊以中醫(yī)為例來說明這個問題。

中醫(yī)辨證施治大體有三個環(huán)節(jié)：收集病人癥候、運用醫(yī)學(xué)知識和據(jù)證立方。

收集病人癥候，就是運用望聞問切的手段，獲得癥候的模糊信息。醫(yī)生占有這種信息量越多，越有利于診斷。然而，過多的癥候信息又會掩蓋主要矛盾，給診斷帶來干擾和困難。為此，西安交通大學(xué)張文修教授提出 “壓縮臨床癥狀資料的數(shù)學(xué)方法”。 他利用熵函數(shù)或權(quán)熵來壓縮那些對診斷疾病不起作用的癥候，利用模糊聚類分析法來壓縮那些對診斷疾病起相似作用的癥候。經(jīng)過反復(fù)壓縮就能夠獲得對診斷疾病起決定作用的癥候。

接著，把能起決定作用的模糊癥侯，用擇近原則歸類，找出癥候替證，再運用模糊不完全歸納推理，求出近似的類型結(jié)論。即：

S1是P1；

S2是P2；

… …

Sn是 Pn；

若 Sn是 S類部分對象

∴ 若 S=UnSi，則 S是 P

這里的i=(1,2,……∞),P是幾個大類的癥候體證。再根據(jù)病情具體分析，確定哪些癥候是首先考慮的，哪些癥候是其次考慮的，排列順序，并加權(quán)系數(shù)，構(gòu)成新的隸屬函數(shù)：

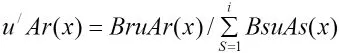
如果病人主訴不清，歸類有困難，可使用浮動閾值技術(shù)。即對第 r種病 Ar，規(guī)定一個閾值 Sr。當(dāng) Ar(x)≥Sr時，便可診斷為病Ar。閾值Sr有一定的浮動范圍，隨r的不同而有所區(qū)別。

運用醫(yī)學(xué)知識據(jù)癥立方，是在實踐的基礎(chǔ)上思辯，進(jìn)行模式識別，力爭為作出最佳決策，猶如下棋或?qū)懳恼乱粯印榇耍仨毥⒁惶啄：壿嫳磉_(dá)式，進(jìn)行有效的似然推理。

基本邏輯推理公式是：G→（E→F）

意即：若病人的癥候為G，醫(yī)學(xué)知識為E，則斷定病人患F病。

常用的推理形式有模糊三段論和模糊假言直言推理。推理結(jié)構(gòu)式，常見的有這種推理一般是根據(jù)模糊關(guān)系的可逆性，從已知的模糊關(guān)系和結(jié)論，倒推出前提來。

廣大醫(yī)生，如果能運用模糊邏輯進(jìn)行醫(yī)學(xué)診斷，將會大大簡化診斷程序，提高治療準(zhǔn)確率，為促進(jìn)人類的健康作出巨大貢獻(xiàn)。

［1］張文修.模糊數(shù)學(xué)基礎(chǔ)[M].西安：西安交通大學(xué)出版社，1984.

［2］曹炳元.應(yīng)用模糊系統(tǒng)與數(shù)學(xué)[M].北京：科學(xué)出版社，2005.

［3］王國俊.計算智能[M]北京：高等教育出版社，2005.