關于“三角形”的糾錯寶典

徐菊萍

同學們，在幾何板塊的學習中，大家常常會將注意力集中在四邊形、圓的研究中，而輕視三角形，其實，三角形作為最簡單的多邊形，是我們研究其他復雜圖形的工具，在中考命題中，有三角形獨立題型，也有三角形知識蘊含在其他幾何圖形中或者代數和幾何的綜合題型中，同學們可不能因小失大.下面就請跟著我一起建立一本關于“三角形”的糾錯寶典吧！

一、角與角之間的關系

1.三角形的角.

例1 （1）在△ABC中，若∠A=2∠B=3∠C，則△ABC是_______三角形.

（2）在△ABC 中，∠A∶∠B∶∠C=1∶2∶3，則△ABC是_______三角形.

【易錯點】誤認為兩題是一樣的解法，都設∠A=x，∠B=2x，∠C=3x，由x+2x+3x=180°，解得x=30°，所以得△ABC是直角三角形.

【分析】（2）中∠A∶∠B∶∠C=1∶2∶3可看出三個角的倍數關系是1份，2份，3份，上述設法正確，而（1）中∠A=2∠B，可知若∠B為1份，則∠A為2份，故應設∠A=x，所以該三角形是鈍角三角形.

【點評】請正確審題，明確角與角之間的份數關系，正確設未知數.可以將所設未知數代入式子進行驗證，如（1）中若設∠A=x，∠B=2x，∠C=3x，代入等式，可發現“x=2×2x=3×3x”這個錯誤的等式.

2.等腰三角形的角.

例2 已知等腰三角形的一個角是40°，則這個三角形的頂角等于________度.

【易錯點】固定思維，認為這個角是底角，由三角形內角和定理得頂角為100°.

【分析】題中未明確給出這個角的信息，故要分類討論，這是數學研究中非常重要的一種思想方法.

（1）當這個角是底角時，可得頂角為100°；

（2）當這個角是頂角時，可直接寫頂角為40°.

因此答案為100°或40°.

【點評】解關于等腰三角形的計算題時，要學會“分類討論”：一個角可能是頂角，也可能是底角；當然，類似的，一條邊可能是腰，也可能是底邊；腰上的高可能在三角形內，也可能在三角形外.

3.直角三角形的角.

例3 （1）將一副三角板如圖1疊放，則圖中α的度數為 __.

（1）如圖2，已知AC⊥BC，垂足為C，AC=4，BC=3 3，將線段AC繞點A按順時針方向旋轉60°，得到線段AD，連接DC，DB.

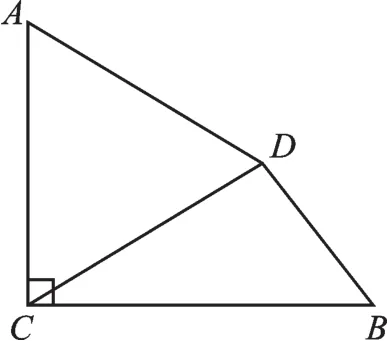
圖2

①線段DC=_______；

②求線段DB的長度.

【易錯點】（1）有同學做該類題時，常常忽略“一副三角板”的默認條件，以為沒有數據而不會解答.

（2）誤認為∠CDB=90°，由①中DC的值，和題中BC的值，利用勾股定理求得DB的長.

【分析】（1）其實這是兩個有已知數據的特殊的直角三角形，直接可以利用三角形的內、外角的知識求解.答案為60°-45°=15°.

（2）△CDB不是直角三角形，因此我們需要構造直角三角形，作DE⊥BC于E，分別解直角△CDE和直角△BDE，如圖3，可得DB=7.

圖3

【點評】觀察圖形是我們求解幾何圖形的第一步，有些圖形正如我們所見，確實是我們所猜想的圖形，當然我們依然要善于從題目中尋找默認的信息或者隱含的條件進行驗證；而有些圖形卻并非如我們所愿，當所給條件不能驗證我們的觀察結論時，我們需要換個角度來求解，比如題（2）中，無法直接得到直角三角形，則構造直角三角形，便于我們求解.

二、邊與邊之間的關系

1.三角形的邊.

例4 （1）三角形的三邊長為3，a，7，則a的范圍是________.

（2）若一個三角形的兩邊長分別為2和4，則該三角形的周長可能是（ ）.

A.6 B.7 C.11 D.12

【易錯點】（1）有的同學答案是3＜a＜7，錯誤認為第三邊的關系是：已知最小邊＜第三邊＜已知最大邊.

（2）不會主動出擊尋找周長的范圍，而是被動地對一個個選項研究，做題沒有目的性.

【分析】靈活運用三角形的三邊關系，即已知三角形的兩邊長，確定第三邊的范圍為：兩邊之差＜第三邊＜兩邊之和，因此：

（1）可得7-3＜a＜7+3，答案為4＜a＜10.

（2）可得第三邊a的范圍為2＜a＜6，周長范圍為8＜l＜12，因此選項為C在此范圍內.

【點評】三角形的三邊關系是我們處理邊與邊關系的前提知識.

2.等腰三角形的邊.

例5 一個等腰三角形的一邊是2cm，另一邊是9cm，則這個三角形的周長是_____cm.

【易錯點】前面我們提醒到，等腰三角形問題常常需要“分類討論”，因此此題三邊有兩種情況：2，2，9以及9，9，2，你也許會回答周長為13cm或20cm，殊不知，你考慮了分類討論，卻忽視了三角形三邊關系的要求.涉及三角形邊的問題時，要判斷給定三條線段能否構成一個三角形，用“三角形兩邊之和大于第三邊”來驗證.

【分析】由于2+2＜9，故2，2，9不能構成三角形，周長只能是20cm.

【點評】由于分類討論涉及多種情況，因此我們要善于對各種類型的答案進行驗證，而不能眉毛胡子一把抓，應該嚴格掌握一些數學定理和規則，有舍有得.

3.直角三角形的邊.

例6 已知一個直角三角形的兩邊是3和4，則第三條邊是________.

【易錯點】常見的勾股數確實為我們平時求解直角三角形的邊長帶來了便利，但是也往往會給我們帶來思維定式，此處答案會有人毫不猶豫地填寫“5”.

【分析】我們再次強調“勾股定理”：直角三角形兩條直角邊的平方和等于斜邊的平方.因此，判斷直角邊和斜邊是我們解題的前提條件，而此題中未給出確切的直角邊和斜邊的信息.因此需要分類討論：

（1）當3和4都是直角邊時，第三邊為斜邊5；

（2）當4是斜邊時，第三邊是直角邊，答案為 7.

所以答案為：5或 7.

【點評】求解直角三角形邊的問題，必須明確哪個角是直角，哪條邊是斜邊，才能正確用好勾股定理，同時大家要辨證看待“勾股數”的作用，為我所用.

三、三角形的三線關系

例7 三角形的重心是（ ）.

A.三角形三條邊上中線的交點

B.三角形三條邊上高線的交點

C.三角形三條邊垂直平分線的交點

D.三角形三條內角平分線的交點

【易錯點】對三角形三類重要的線段不熟悉，會導致張冠李戴，胡亂選擇選項.

【分析】三角形的三類重要的線段：（1）高線——交點為垂心；（2）角平分線——交點為內心；（3）中線——交點為重心.另外還有一類重要的直線：三條邊垂直平分線——交點為外心.你可以在四個三角形中分別作出四個心，數形結合來掌握這個結論，避免死記硬背導致混淆答案.

【點評】內心和外心還需要結合內切圓和外接圓的知識，你可以畫一棵知識樹，幫助自己辨析概念，靈活運用相關知識.

2.等腰三角形的三線.

例8 如圖4，在△ABC中，AB=AC，AD⊥BC，垂足為點D，若∠BAC=70°，則∠BAD=___°.

圖4

【分析】此題一般都能求解，這里特地拿出來是為了強調解題的方法，很多同學迷戀全等三角形，涉及求邊相等、角相等的問題，第一反應是利用三角形全等的知識，而忽略了有些更便捷的方法.本題也能利用全等三角形證明，但利用等腰三角形三線合一的方法將簡單得多.由AB=AC，AD⊥BC，根據等腰三角形三線合一的性質，得∠BAD=∠CAD，由∠BAC=70°，則∠BAD=35°.

【點評】熟記等腰三角形“三線合一”定理：等腰三角形的頂角平分線、底邊上的中線、底邊上的高互相重合.

3.直角三角形的三線.

例9 直角三角形的兩直角邊分別為5cm，12cm，其中斜邊上的高為（ ）.

【易錯點】“等積法”在直角三角形求線段問題中非常常見，我們可以輕松求得該直角三角形的斜邊長為13cm，面積為30cm2，然后直接用30除以13，選C.

【分析】三角形面積是底乘高的一半，很多同學會忽略“一半”，上面解法的錯誤就在于直接用面積除以底，而忘了“一半”的處理，為防止這個錯誤，我們可以由三角形的面積公式得斜邊上的高為，此處兩次計算面積中用到的“一半”同時抵消了，避免了錯解.

【點評】我們也可以用方程思想來求解這題，設斜邊上的高為x，可得方程5×12，解這個方程，則不會受-的干擾.