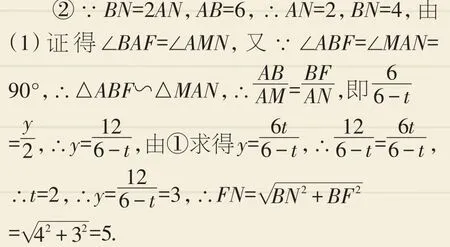動靜結合的四邊形中考題

萬廣磊

在歷年的中考題中，四邊形是必考內容，主要通過靜態的圖形呈現和動態的圖形變換（翻折、旋轉、平移等），實現對四邊形的邊角關系和特殊的平行四邊形（含矩形、菱形、正方形）的判定與性質進行考查，還要綜合運用化歸、函數、方程等思想方法進行計算.下面以2017年幾道中考試題為典型進行剖析，以期對同學們有所啟發.

一、多邊形的計算

例1 （2017·蘇州）如圖1，在正五邊形ABCDE中，連接BE，則∠ABE的度數為（ ）.

A.30° B.36° C.54° D.72°

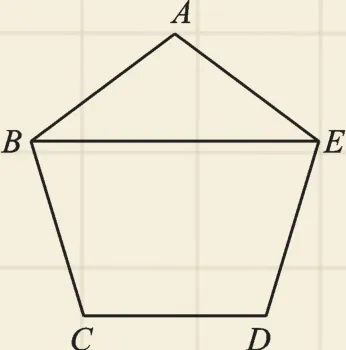
圖1

【思路分析】本題考查了正五邊形的內角和以及等腰三角形的性質，解題的關鍵是求出正五邊形的每個內角的度數.可以先根據多邊形的內角和公式求出內角和，求出每個內角的度數，再結合△ABE是等腰三角形，求出底角的度數.

【解答過程】∵已知正五邊形ABCDE，∴五邊形ABCDE內角和等于（5-2）×180°=540°，∴每一個內角為540°÷5=108°，又∵AB=AE，∴∠ABE=（180°-108°）÷2=36°，故選B.

【另法點撥】此題也可根據正五邊形的外角和是360°，求出每個外角為72°，相鄰內角就是108°，從而得到底角的度數是36°.

二、平行四邊形的判定與性質

例2 （2017·鎮江）如圖2，點B、E分別在AC、DF上，AF分別交BD、CE于點M、N，∠A=∠F，∠1=∠2.

（1）求證：四邊形BCED是平行四邊形；

（2）已知 DE=2，連接 BN，若 BN 平分∠DBC，求CN的長.

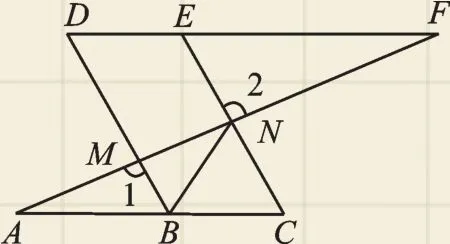
圖2

【思路分析】本題考查了平行四邊形的判定與性質、等腰三角形的判定，解題的關鍵是利用兩組對邊分別平行判定平行四邊形，再應用平行四邊形的性質求得線段長.第（1）問，根據條件中已有角的相等關系，判斷四邊形的兩組邊分別平行，進而確定四邊形是平行四邊形；第（2）問用平行四邊形的性質和角平分線可得等腰△BCN，進而將求線段CN的長轉化為求BC的長.

【解答過程】（1）證明：∵∠A=∠F，∴DF∥AC.又∵∠1=∠2，∠1=∠DMF，∴∠2=∠DMF，∴DB∥EC，∴四邊形BCED是平行四邊形.

（2）解：∵BN平分∠DBC，∴∠DBN=∠NBC，∵DB∥EC，∴∠DBN=∠BNC，∴∠NBC=∠BNC，∴BC=CN.∵四邊形BCED是平行四邊形，∴BC=DE=2，∴CN=2.

【規律總結】在問題（2）中，平行線與角平分線的條件組合，可得等腰三角形，這是一個幾何基本圖形.

三、三角形的中位線性質

例3 （2017·懷化）如圖3，在?ABCD中，對角線AC，BD相交于點O，點E是AB的中點，OE=5cm，則AD的長為 cm.

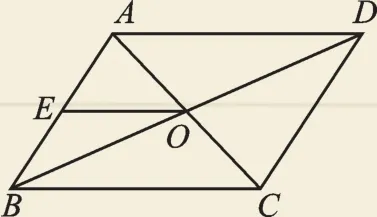
圖3

【思路分析】本題考查了平行四邊形的性質和三角形中位線的性質，解題的關鍵是確定OE是三角形的中位線.利用平行四邊形的對角線性質和點E是AB的中點，可得OE是△BAD的中位線，從而求出AD的長.

【解答過程】∵四邊形ABCD為平行四邊形，∴點O為BD的中點.又∵點E是AB的中點，∴OE是△BAD的中位線，則AD=2OE=2×5=10.故答案為10.

【易錯點睛】本題易錯點是不能由平行四邊形的性質得到O為BD的中點，從而不能確定OE是△BAD的中位線.

四、矩形的判定與性質

例4 （2017·宿遷）如圖4，在矩形紙片ABCD中，已知AB=1，BC=3，點E在邊CD上移動.連接AE，將多邊形ABCE沿直線AE折疊，得到多邊形AB′C′E，點B、C的對應點分別為B′、C′.

（1）若當B′C′恰好經過點D時（如圖4），求線段CE的長；

（2）若B′C′分別交邊AD、CD于點F、G，且∠DAE=22.5°（如圖5），求△DFG的面積；

（3）在點E從點C移動到點D的過程中，求點C′運動的路徑長.

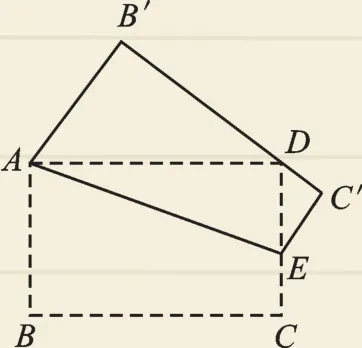
圖4

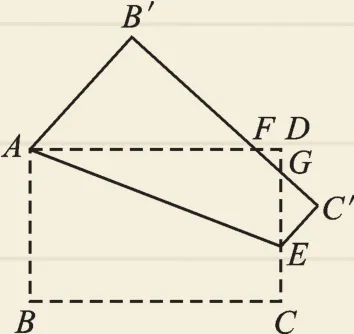
圖5

【思路分析】本題是幾何壓軸題，綜合考查了矩形的性質、相似三角形的性質與判定、等腰直角三角形的性質與判定、勾股定理、弧長的計算等知識，解題的關鍵是利用勾股定理或相似三角形知識計算出相關線段的長，找到C′點運動的路徑并用弧長公式進行計算即可.（1）在Rt△AB′D中，先由勾股定理求出B′D的長，進而得到C′D的長，然后利用勾股定理得到關于CE（令CE=x）的一元一次方程x2+解方程即可得到CE的長；或者利用相似三角形的知識，通過證明△ADB′∽△DEC′，得到

（2）∵四邊形ABCD是矩形，∴∠BAD=∠ADC=90°.∵∠DAE=22.5°，∴∠BAE=∠B′AE=67.5°，∴∠B′AD=67.5°-22.5°=45°.又∵∠B′=90°，AB′=AB=1，∴AF=2，FD=3-2.∵∠AFB′，也可求出CE的長.（2）先判斷△AFB′是等腰直角三角形，并求出AF的長，進而求出DF的長；然后再判斷△FDG是等腰直角三角形，進而求出該三角形的面積.（3）連接AC′，則AC′=AC=2，在點E從點C移動到點D的過程中，點C′運動的路徑是以點A為圓心，AC長為半徑且圓心角為60°的扇形弧長，最后進行弧長計算即可.=45°，∠D=90°，∴∠DFG=45°，△DFG 是等腰直角三角形，

（3）如圖6，連接AC，在Rt△ABC中，由勾股定理，得AC=2.∵=60°，∠CAD=30°.當點E與點D重合時，∠C′AD=30°.∴在點E從點C移動到點D的過程中，點C′運動的路徑是以點A為圓心，AC長為半徑且圓心角為60°的扇形弧長，而l弧=故點C′運動的路徑長

圖6

【易錯點睛】本題容易出錯的地方有三處：一是在解答第（1）問時，因二次根式計算出錯；二是在解第（2）問時，不能充分利用∠DAE=22.5°判斷圖2中的兩個等腰直角三角形，導致解題束手無策；三是找不到點C′運動的路徑，不能求出點C′運動的路徑長.

【規律歸納】翻折變換是幾何中常用的幾何變換，解題時要充分利用翻折前后的兩個圖形對應線段相等、對應邊相等的性質.本題的前兩問，都是基于這個性質來求解線段的長和三角形的面積的.對于最后一個問題，可以在備用圖上先找幾個特殊的點E的位置，看看點C′的相應位置，再利用C′點到A點的距離不變皆為2，這就尋找到C′的運動軌跡即是以點A為圓心，AC長為半徑且圓心角為60°的扇形弧長，弧長的計算公式為

五、菱形的判定與性質

例5 （2017·濱州）如圖7，在?ABCD中，以點A為圓心，AB長為半徑畫弧交AD于點F；再分別以點B、F為圓心，大于BF的相同長為半徑畫弧，兩弧交于點P；連接AP并延長交BC于點E，連接EF，則所得四邊形ABEF是菱形.

（1）根據以上尺規作圖的過程，求證四邊形ABEF是菱形；

（2）若菱形ABEF的周長為16，AE=4 3，求∠C的大小.

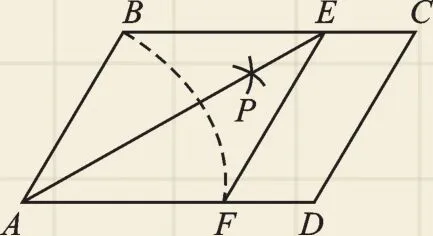
圖7

【考點解剖】本題綜合考查了尺規作角平分線、菱形的性質與判定、平行四邊形的性質、解直角三角形.解題的關鍵是根據尺規作圖的作法得題目的條件.（1）由“平行線+角平分線”構造等腰三角形，然后利用AB=AF（作法）得BE=AF，再根據BE∥AF完成證明；（2）根據菱形的性質，將所給線段的條件轉移到同一直角三角形中，利用邊的關系得角的度數，然后利用菱形的性質及平行四邊形的性質得∠C的度數.

【解答過程】（1）由作圖過程可知，AB=AF，AE平分∠BAD，∴∠BAE=∠EAF.∵四邊形ABCD為平行四邊形，∴BC∥AD，∴∠AEB=∠EAF，∴∠BAE=∠AEB，∴AB=BE，∴BE=AF，∴四邊形ABEF為平行四邊形，又∵AB=AF，∴?ABEF為菱形.

（2）連接BF，交AE于點O.

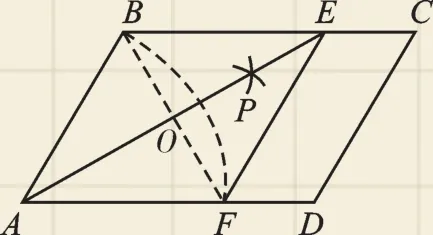
圖8

【易錯點睛】本題的易錯點是無法從尺規作圖的作法中獲取條件，導致無法完成證明.

六、正方形的判定與性質

例6 （2017·菏澤）正方形ABCD的邊長為6cm，點E、M分別是線段BD、AD上的動點，連接AE并延長，交邊BC于F，過M作MN⊥AF，垂足為H，交邊AB于點N.

（1）如圖9，若點M與點D重合，求證：AF=MN.

（2）如圖10，若點M從點D出發，以1cm/s的速度沿DA向點A運動，同時點E從點B出發，以 2cm/s的速度沿BD向點D運動，運動時間為ts.

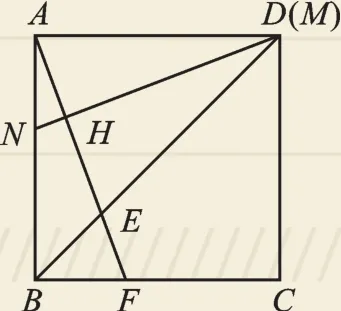
圖9

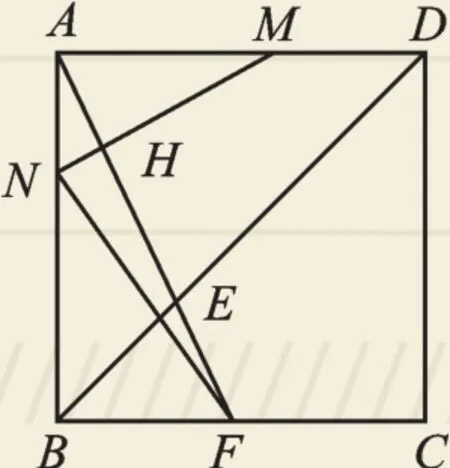
圖10

①設BF=ycm，求y關于t的函數表達式；

②當BN=2AN時，連接FN，求FN的長.

【考點解剖】本題考查了正方形的性質、全等三角形的判定和性質、相似三角形的判定和性質，解題的關鍵是利用全等三角形和相似三角形證明線段的關系.（1）直接利用兩角一邊證明△AMN≌△BAF即可.（2）①過點E作EG⊥AB，垂足為G，利用△AEG∽△AFB即可得到結論；②結合前兩個題目的條件可證明△AEG≌△MNA，從而求得t的值，代入①可求得BF，再利用勾股定理進行解答.

【解答過程】（1）證明：∵四邊形ABCD是正方形，∴∠DAB=∠ABC=90°，AB=AD，∴∠BAF+∠FAM=90°；∵MN⊥AF，∴∠FAM+∠AMN=90°，∴∠AMN=∠BAF，∴△AMN≌△BAF，∴AF=MN.

（2）①過點E作EG⊥AB，垂足為G.

由題意得，DM=t，BE=2t，∵四邊形ABCD是正方形，∴∠ABD=45°，∴GE=GB=t，∴AG=6-t.∵AB⊥BC，∴GE∥BF，

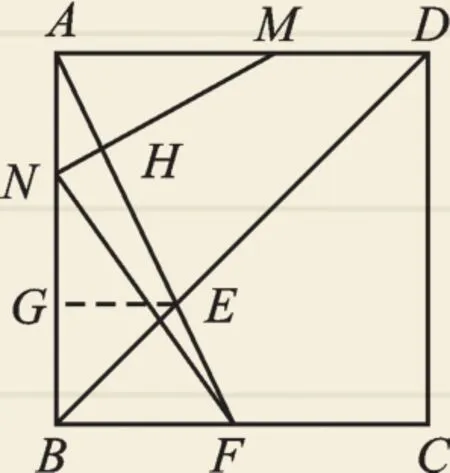
圖11

②∵BN=2AN，AB=6，∴AN=2，BN=4，∵AM=6-t，AG=6-t，∴AM=AG.

由（1）證得∠BAF=∠AMN，∵∠AGE=∠MAN=90°，∴△AEG≌△MNA，∴EG=AN，∴t=2，∴在 Rt△BFN 中 ，FN=

【規律歸納】四邊形的幾何證明題一般都需要用全等或相似作為工具來進行證明，在應用全等或相似三角形的判定時，要注意三角形間的隱含條件，如公共邊、公共角、對頂角、直角、余角等，必要時添加適當輔助線構造三角形.

【一題多解】本題還可以這樣解答：

（2）①∵AB=AD=6，∴BD=6 2，由題意得，DM=t，BE=2t，∴AM=6-t，DE=6 2-2t，∵AD∥BC，∴△ADE∽△FBE，∴