低頻缺失下跨孔雷達包絡波形反演

劉新彤,劉四新, 孟 旭,傅 磊

1.吉林大學地球探測科學與技術學院，長春 130026 2.澳門科技大學太空科學研究所，澳門 999078

0 引言

跨孔探地雷達層析成像技術不斷發展，已經在水文、環境和工程物探中得到了驗證與有效應用。在數據采集過程中，跨孔雷達將兩個天線放置在相隔一定距離的兩個井孔中，一個作為發射源，另一個作為接收器。發射天線發出的雷達波穿過井孔之間的介質被接收天線采集，該雷達波包含井孔之間介質的物性參數(如介電常數和電導率)空間分布信息。傳統的走時層析成像和衰減層析成像技術雖然可以分別有效地反演出地下介質的介電常數和電導率分布情況，但由于上述方法基于射線理論，僅僅使用了雷達波的部分信息，因而所得到的結果分辨率有限。跨孔雷達全波形反演技術在反演過程中使用雷達波的全部信息，所得到的地下介質物性參數分布結果的分辨率可以達到亞波長級別。

近些年來，國際地球物理探測學界對全波形反演(full waveform inversion， FWI)方法持續關注，波形反演技術在很多領域都取得了顯著進展，尤其是在地震方面，已經得到了相對成熟的理論架構。早期，Tarantola[1]將廣義最小二乘反演理論應用到了全波形反演方法中，通過合成數據與觀測數據計算出殘差并進行反傳獲得反傳波場，利用反傳波場與正傳波場的互相關來構建梯度，形成了一套完整的時間域波形反演方法理論架構。隨后，Pratt等[2-4]將全波形反演方法擴展到了頻率域，提出頻率域全波形反演方法；馮晅等[5]提出基于逐減隨機震源采樣法的頻率域波形反演方法。與地震全波形反演方法相比，探地雷達全波形反演方法的研究起步較晚，且目前仍然處于發展初期。Kuroda等[6]采用全波形反演方法來解釋跨孔雷達數據，獲得了介電常數成像結果。Ernst[7]等使用全波形反演方法處理跨孔雷達數據，采用級聯更新的方式同時反演了介電常數和電導率，并取得了較好的效果。Meles等[8]利用矢量全波形反演技術處理探地雷達數據，進行了同時迭代介電常數和電導率的全波形反演。在國內，波形反演也取得了一定的進展。吳俊軍等[9]利用攝動法求解全波形反演的目標函數并詳細推導了基礎理論，采用最速下降法在迭代過程中同時更新介電常數和電導率；孟旭等[10]進一步將跨孔雷達全波形反演方法發展到了頻率域，推導了基于對數目標函數的頻率域全波形反演的基礎理論，使用共軛下降法同時反演介電常數和電導率。在處理實際數據方面，Ernst等[11]提出一種二維全波形反演策略，采用級聯方式反演兩種物性參數，反演跨孔雷達實際數據。但是，到目前為止，由于實際數據信噪比較低，國內外使用全波形反演方法處理探地雷達實際數據并沒有得到良好的應用。

FWI方法廣泛采用局部優化的方式進行反演，但由于其本身對初始模型高度依賴，面對先驗信息缺失的地下介質時，無法從準確的初始模型出發；且在實際采集到的數據中包含噪聲以及存在低頻信息缺失的情況下，局部優化方法很容易陷入局部極值[12]。在目前的波形反演研究領域中，普遍選擇為其構建較為準確的初始模型，來降低非線性程度以獲取更好的結果。而對于構建大尺度的初始模型，低頻信息的使用尤為關鍵。對于實際數據，由于帶寬或數據采集濾波器設計等原因，低頻信息往往難以采集；雖然在實驗室條件下能夠采集到一定量的低頻數據，但是難度極高，成本巨大，所采集到的數據并不完整且應用難度較大，無法推廣到探地雷達野外數據的處理中。以中心頻率為100 MHz的鉆孔雷達為例，難以獲得30 MHz以下的有效信息。因此，重新構建探地雷達數據中的有效低頻信息，成為了利用全波形反演方法處理跨孔雷達數據的重點。

本文在時間域跨孔雷達波形反演的基礎上，使用包絡目標函數，采用求導法，詳細推導了包絡波形反演(EWI)方法的基礎理論，將EWI成功推廣到了探地雷達(ground penetrating radar，GPR)領域，并采用共軛梯度法同時反演了兩種物性參數(介電常數和電導率)；通過模擬原始數據低頻信息缺失的情況驗證該方法在低頻缺失情況下的反演能力，反演結果在為地下介質做出評價的同時，可以作為初始模型，降低非線性程度，進一步參與到傳統波形反演當中， 來獲取分辨率更高的結果。該全波反演方法的正演部分采用高階時間域有限差分算法，使用了CPML(convolutional perfect matched layer)吸收邊界，并在每一次迭代過程中，對梯度進行了中值濾波等優化方式。由于反演過程中數據量巨大，采用了Matlab的分布式計算引擎(matlab distributed computing engine， MDCE)并行運算的方式，以提高在普通微機上的運行效率。

1 正演問題表達形式

在討論探地雷達地球物理問題時，地下介質的物性參數分布情況使用介電常數和電導率來描述，并假設磁導率是均勻不變的。在時間域，對于任意時間點t和空間x，Maxwell方程如下[7]：

(1)

式中：ε(x)和σ(x)分別表示介電常數和電導率的空間分布；s表示某一個特定的源；μ0表示磁導率，這里假定為常數；Es和Hs分別表示由電流密度源矢量Js產生的電場和磁場。式(1)可簡寫成如下形式：

(2)

式中，M(ε,σ)代表Maxwell方程的一個線性算子。忽略磁場項：

MEs=Js或Es=M-1Js。

(3)

在時間域，空間任意位置的電場可以用源與對應位置格林函數之間的卷積來表示：

Es=g*Js。

(4)

式中，g為M算子對應的格林函數。顯然，M-1包含離散近似的格林函數[2-4]。因此，

M-1=g。

(5)

2 目標函數及梯度計算

2.1 傳統全波形反演

傳統全波形反演的主要目的是尋找目標函數最小時對應的介電常數ε與電導率σ的空間分布。傳統目標函數表達式為

(6)

式中：d表示接收器；τ表示觀測時間；E(ε,σ)和Eobs分別為電場正演數據和實際數據。式(6)表示源s在接收點d處、觀測時間為τ時全部誤差的總和。目標函數對應的梯度由正傳合成波場與反傳伴隨波場的互相關獲得：

(7)

式中：p代表模型參數ε和σ；v為虛擬源向量，對于不同的模型參數具有不同的表達式；r(ξ)=E(ξ)-Eobs(ξ)，代表反傳波場的后向殘場源。

2.2 包絡波形反演

本文通過將包絡目標函數引入到Meles等[7]的矢量波形反演技術當中，重新構建包絡全波形反演基礎理論。不同于Meles等使用擾動目標函數一階近似來推導梯度的方法，本文使用對包絡目標函數求導的方式來推導梯度。式(6)為反演中最廣泛使用的傳統目標函數，本文給出基于該目標函數基礎上的包絡目標函數，即合成包絡波場與實際包絡波場差的2-范數：

(8)

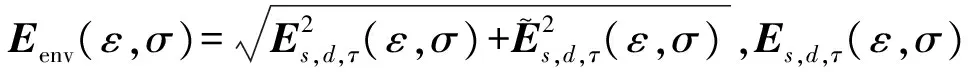
(9)

進一步推導獲得

(10)

式中，對合成波場的偏微分可以通過使用模型參數p對公式(3)兩端求偏導獲得：

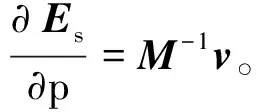
(11)

其中，

(12)

在時間域，空間任意位置的電場可以認為是源與對應位置格林函數之間的卷積：

(13)

其中，

(14)

將式(5)代入式(13)并寫成積分的形式：

(15)

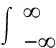
(16)

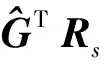
(17)

為了實現最大程度的收斂，本文使用共軛梯度法來更新模型：

[ε(x)k+1]=[ε(x)k]-ζε,k·[Cε(x)k]，

(18)

[σ(x)k+1]=[σ(x)k]-ζσ,k·[Cσ(x)k]。

(19)

式中：ζε,k和ζσ,k分別為第k次迭代中介電常數和電導率的迭代步長；Cε(x)k和Cσ(x)k分別為介電常數和電導率對應的共軛梯度方向，由當前和上一次的梯度計算得到。

Cε(x)k=Sε(x)k+

(20)

Cσ(x)k=Sσ(x)k+

(21)

當k=1時，滿足Cε(x)1=Sε(x)1和Cσ(x)1=Sσ(x)1。通過沿各自Cε、Cσ方向尋找極值點，我們能夠在同一次迭代中實現介電常數和電導率的同步反演。迭代步長由以下公式獲得：

[Eenv(ε+κεCε,k,σ)-Eenv(ε,σ)]，

(22)

[Eenv(ε,σ+κσCσ,k)-Eenv(ε,σ)]。

(23)

式中，κε、κσ為不同的小穩定因子。在反演過程中必須小心地為其選擇適當的值并且該值隨著迭代不斷更新。

3 數值模擬

與傳統的FWI方法對比完整波形不同，我們的方法比較的是合成數據的包絡與觀測數據的包絡。這里我們以Ricker子波為例來分析包絡轉換的作用。圖1a顯示了一道Ricker子波的波形與它對應的包絡,通過對比可以看出，Ricker子波信號本身變化劇烈，而包絡波形變化相對緩慢。圖1b為子波頻譜與包絡頻譜的對比圖，可以很明顯看出存在低頻信息通過非線性轉換被加入到了包絡頻譜中。

傳統的跨孔雷達FWI在雷達數據低頻信息充足且初始模型足夠準確的情況下可以獲得良好的反演結果；但是當低頻信息缺少時，FWI方法往往無法恢復大尺度的背景信息，甚至錯誤地更新模型并導致反演最終無法收斂，非常容易陷入局部最小。雷達數據缺少低頻信息這種狀況在很多雷達實例中存在，面對類似情況的實例，FWI方法難以發揮作用；但EWI方法有能力在數據缺少大量低頻信息的情況下更新模型的長波長信息，其原因是它的伴隨波場含有低頻信息。我們去除Ricker子波30 MHz以下的低頻成分，圖2a中為去除低頻成分后的Ricker子波及其包絡，可以看出去除低頻成分后，Ricker子波信號變動更劇烈，而包絡曲線依然平穩。圖2b為其頻譜對比圖，與圖1b相比較，可以非常明顯地看出，在除去低頻成分后，Ricker子波頻譜低頻部分雖然被移除，但其包絡低頻部分幾乎不受影響，仍然有明顯的低頻信息被添加。

為了驗證EWI方法的成像能力，我們建立了如圖3所示的復雜小模型，模型尺寸為6 m×6 m，包含3個地層：第一層與第三層物性參數相同，相對介電常數均為5，電導率為0.001 S·m-1；中間層的相對介電常數為5.5，電導率為0.002 8 S·m-1，并埋藏兩個柱狀異常體，位于深度3 m處，間隔1 m，相對介電常數為7，電導率為0.008 S·m-1。在本次模擬中共13個發射源，每組發射對應13個接收器。發射器與接收器位置均為深度0～6 m，并以0.5 m等間隔排列；天線中心頻率為100 MHz。

首先，我們對比了兩種方法基于均勻初始模型反演的結果。均勻初始模型的相對介電常數為5.5，電導率為0.002 8 S·m-1。初始模型物性參數與原始模型中間層背景物性參數一致。由于原始數據包含了完整且正確的長波長信息，所以FWI和EWI兩種反演方法均能夠獲得良好的反演結果。其中傳統的全波形反演方法所得到的結果分辨率略高于基于包絡的波形反演結果，這是因為FWI方法使用的信息更加完整，但也有更高的非線性程度。從圖4反演結果來看，FWI方法在波形信息完整時，反演結果要優于EWI方法，尤其對于中間兩個管線異常體，傳統波形反演電導率結果優勢明顯。

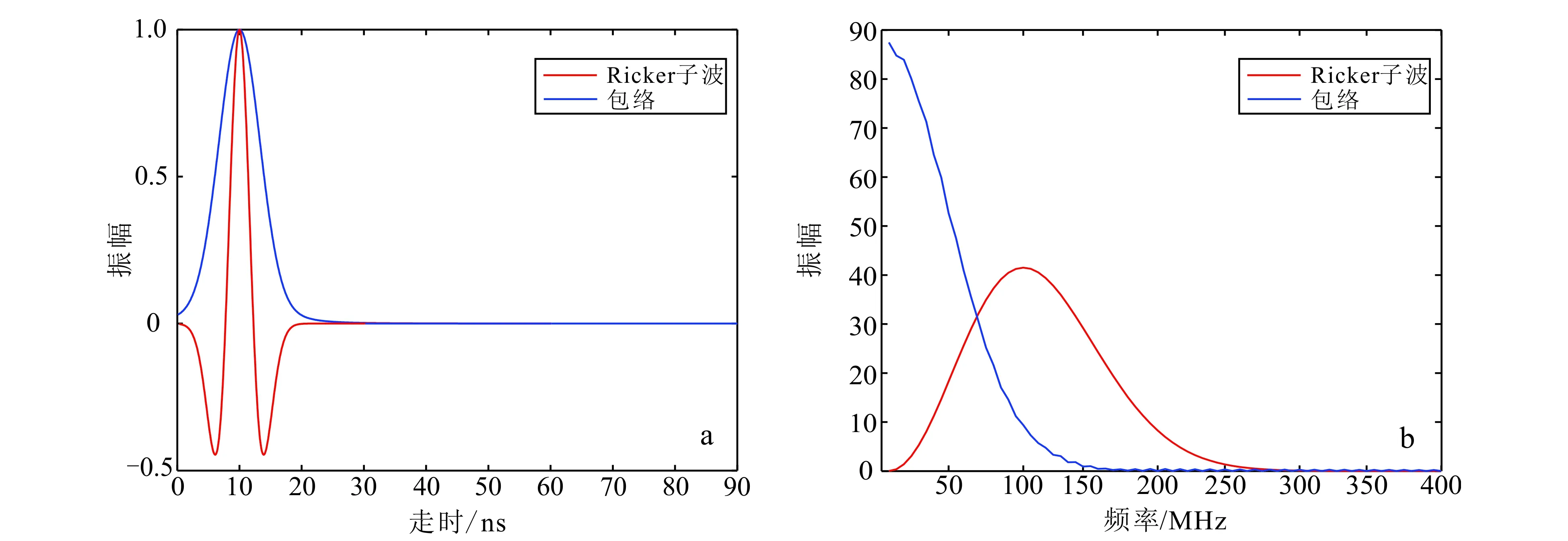
圖1 Ricker子波和包絡波形(a)及其頻譜(b)Fig.1 Ricker wavelet and its envelope (a) and spectrum (b)

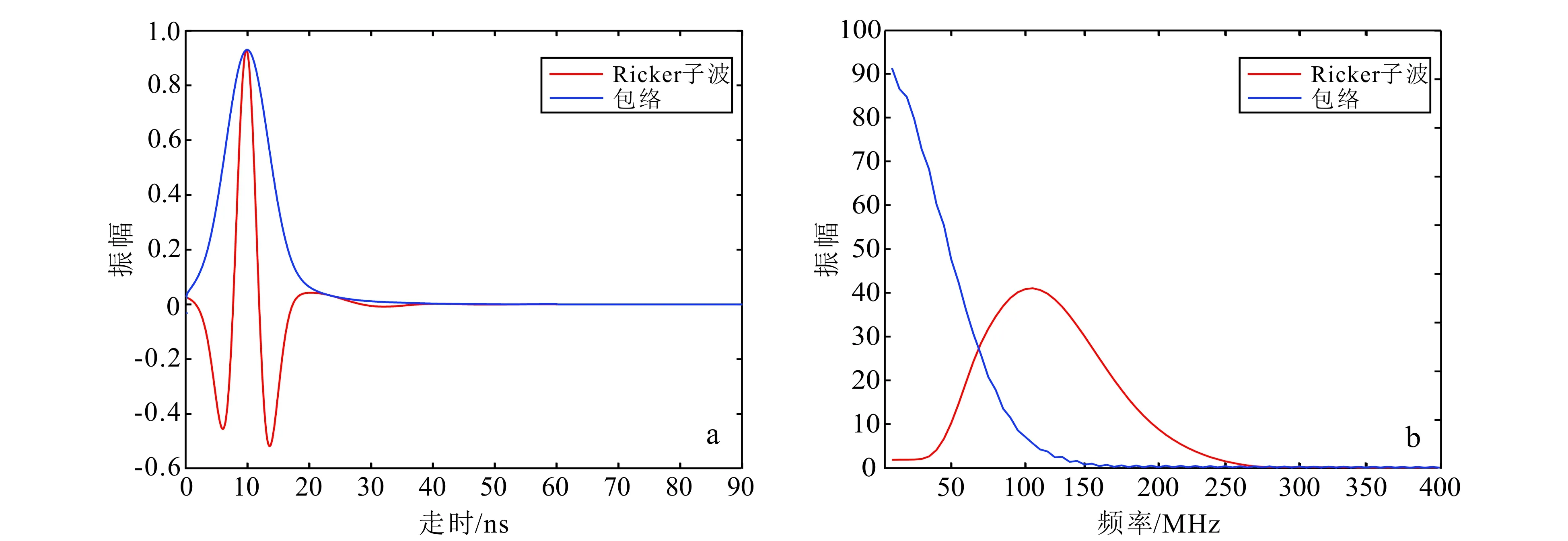
圖2 去除30 MHz以下低頻成分Ricker子波及其包絡(a)和頻譜(b)Fig.2 Ricker wavelet without low frequency data under 30 MHz and its envelope (a) and spectrum (b)

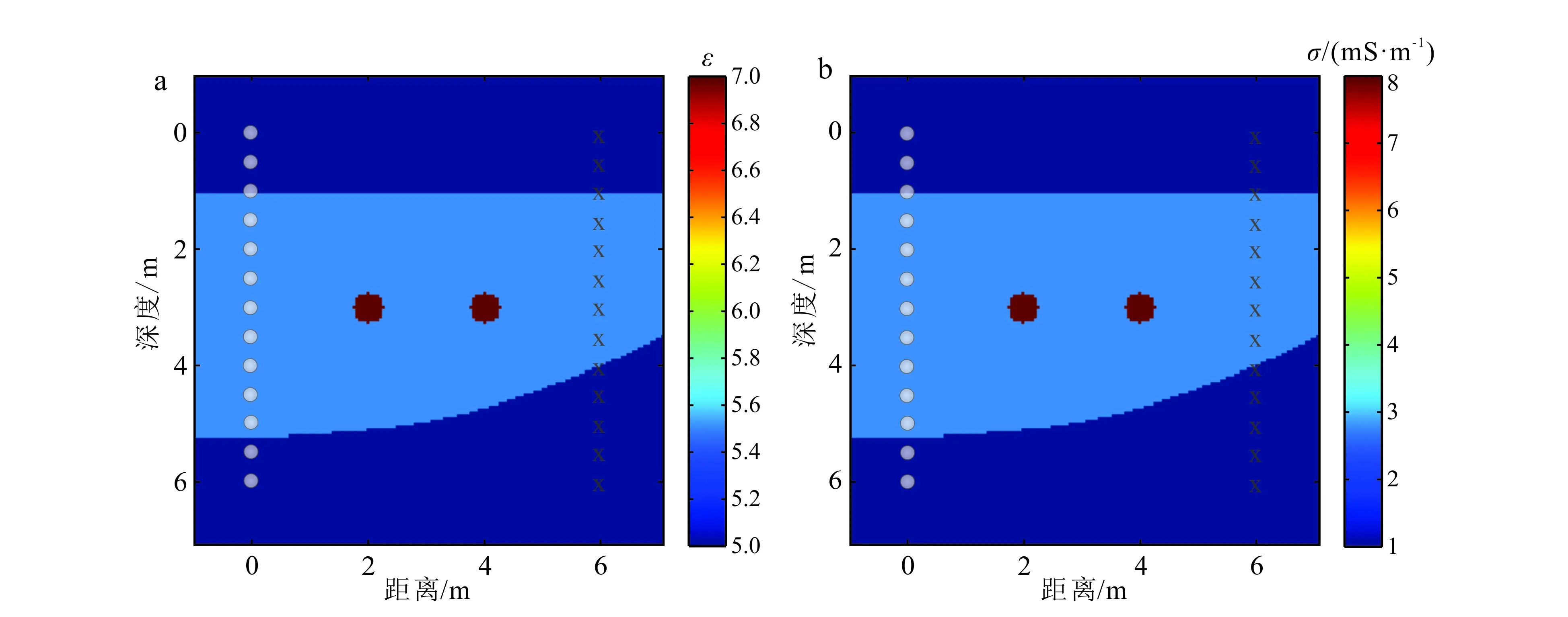
a.相對介電常數；b.電導率。白色圓圈表示發射源，叉號表示接收器，下同。圖3 原始模型Fig.3 Original model

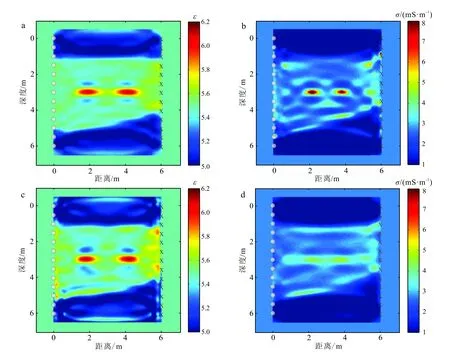
a、b. FWI；c、d. EWI。圖4 完整頻率信息波形反演結果Fig.4 Waveform inversion results of complete frequency information

接著，我們提取了原始數據30 MHz以下的低頻信息，以驗證FWI和EWI兩種方法對低頻信息的反演能力。如圖5所示，FWI方法在單獨反演低頻信息時，反演能力明顯下降，圖5a、b是迭代20次的結果，雖然能夠反演出一定的地層和異常體信息，但已經遠遠不及EWI方法(圖5c、d)；并沒有選擇更多的迭代次數是因為由于低頻缺失，FWI方法容易陷入局部最小，隨著迭代的進行，結果將會朝著錯誤的方向發展，最終無法收斂，完全無法準確反映地下信息。而包絡波形反演能夠獲得良好的結果，目標函數收斂，且最終結果(圖5c、d)與圖4中使用全部波形信息反演的結果相差不大。該組模擬證明，EWI方法對低頻信息的利用能力高于FWI方法。對比提取低頻信息的反演結果與完整波形信息的反演結果可以看出，無論使用FWI還是EWI方法，由于高頻信息的缺失，反演對于中間細節的刻畫明顯下降，極易陷入局部最小。

最后，我們模擬現實中低頻缺失的情況，以了解當低頻缺失、FWI方法無法獲得理想反演結果的情況下，EWI方法是否仍然可以獲得良好結果，使跨孔雷達波形反演體系更加完善且更符合實際應用。圖6中，由于相同的原因，FWI結果與圖5一致，均為20次迭代的結果。由圖6可見：在低頻信息缺失的情況下，無論是介電常數還是電導率，FWI均無法獲得與利用完整波形信息進行FWI時一致的結果，目標函數不收斂；與FWI相對比，EWI的結果更好，且目標函數收斂，能夠為地下地層與異常體從位置和物性參數方面提供定量解釋。

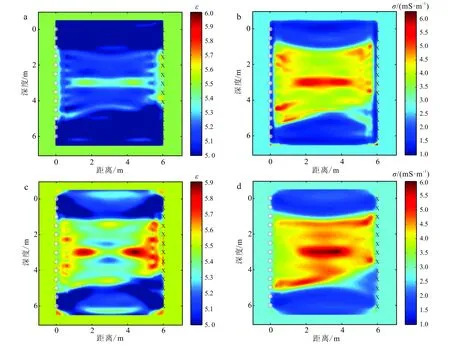
a、b. FWI；c、d. EWI。圖5 30 MHz以下低頻信息反演結果Fig.5 Inversion result of low frequency data under 30 MHz

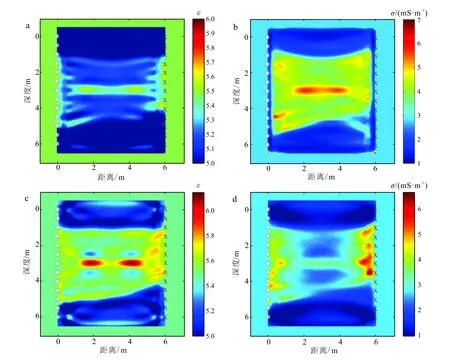
a、b. FWI；c、d. EWI。圖6 去除30 MHz以下低頻信息反演結果Fig.6 Inversion result without low frequency under 30 MHz

4 結論

1)與全波形反演方法相比，包絡波形反演方法是一種對頻率成分更加穩定且非線性更低的波形反演方法。跨孔雷達數值模擬證明該方法在跨孔雷達領域有著很高的應用價值，尤其對于低頻信息缺失的數據，包絡波形反演可以在傳統波形反演不適用的情況下仍然提供良好的反演結果。

2)雖然對于完整的波形信息，全波形反演方法結果要優于包絡波形反演的結果，尤其在電導率的結果上全波形反演方法優勢明顯；但在低頻信息缺失時，包絡波形反演無論是介電常數還是電導率，結果明顯優于全波形反演方法，可以為地下物性參數提供解釋。

3)包絡波形反演方法是對跨孔雷達波形反演的一種補充方法，使得跨孔雷達波形反演符合更多應用實例。

[1]Tarantola A. Inversion of Seismic-Reflection Data in the Acoustic Approximation [J]. Geophysics, 1984, 49: 1259- 1266.

[2] Pratt R G, Shin C, Hicks G J. Gauss-Newton and Full Newton Methods in Frequency Domain Seismic Waveform Inversion [J]. Geophysical Journal International, 1998, 133: 341-362.

[3] Pratt R G. Seismic Waveform Inversion in the Fre-quency Domai: Part 1: Theory and Verification in a Physical Scale Model [J]. Geophysics, 1999, 64: 888-901.

[4] Pratt R G, Shipp R M. Seismic Waveform Inversion in the Frequency Domain: Part 2: Fault Delineation in Sediments Using Crosshole Data [J]. Geophysics, 1999, 64: 902-914.

[5] 馮晅, 魯曉滿, 劉財,等. 基于逐減隨機震源采樣法的頻率域二維黏滯聲波方程全波形反演[J]. 吉林大學學報(地球科學版), 2016, 46(6):1865-1873.

Feng Xuan, Lu Xiaoman, Liu Cai, et al. Frequency-Domain Full Waveform Inversion of 2D Viscous Acoustic Wave Equation Using Decreasing Random Shot Subsampling Method[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1865- 1873.

[6] Kuroda S, Takeuchi M, Kim H J. Full Waveform In-version Algorithm for Interpreting Cross-Borehole GPR Data [J]. Seg Technical Program Expanded Abstracts, 1949, 24(1): 2668.

[7] Ernst J R, Maurer H, Green A G, et al. Full-Wave-form Inversion of Crosshole Radar Data Based on 2-D Finite-Difference Time-Domain Solutions of Maxwell’s Equations [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(9): 2807-2828.

[8] Meles G A, Kruk J V D, Greenhalgh S A, et al. A New Vector Waveform Inversion Algorithm for Simultaneous Updating of Conductivity and Permittivity Parameters from Combination Crosshole/Borehole-to-Surface GPR Data [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(9): 3391-3407.

[9] 吳俊軍,劉四新,李彥鵬,等．跨孔雷達全波形反演成像方法的研究[J]. 地球物理學報, 2014, 57(5):1623-1635.

Wu Junjun, Liu Sixin, Li Yanpeng, et al. Study of Cross-Hole Radar Tomography Using Full-Waveform Inversion [J]. Chinese Journal of Geophysics, 2014, 57(5): 1623-1635.

[10] 孟旭, 劉四新, 傅磊,等. 基于對數目標函數的跨孔雷達頻域波形反演[J]. 地球物理學報,2016,59(5):1875-1887.

Meng Xu, Liu Sixin, Fu Lei, et al. Frequency Domain Waveform Inversion of Cross-Hole GPR Data Based on a Logarithmic Objective Function [J]. Chinese Journal of Geophysics, 2016, 59(5):1875-1887.

[11] Ernst J R, Green A G, Maurer H, et al. Application of a New 2D Time-Domain Full-Waveform Inversion Scheme to Crosshole Radar Data [J]. Geophysics, 2007, 72(5): J53-J64.

[12] Virieux J, Operto S. An Overview of Full-Waveform Inversion in Exploration Geophysics [J]. Geophysics, 2009, 74 (6), WCC1-WCC26.

[14]Chi B X, Dong L G, Liu Y Z. Full Waveform Inversion Based on Envelope Objective Function [C]// 75th EAGE Conference & Exhibition Incorporating Spe Europec 2013. London: EAGE, 2013.

[15]Chi B X, Dong L G, Liu Y Z. Full Waveform Inversion Method Using Envelope Objective Function Without Low Frequency Data [J]. Journal of Applied Geophysics, 2014, 109: 36-46.

[16]Wu R S, Luo J R, Wu B Y. Seismic Envelope Inversion and Modulation Signal Model [J]. Geophysics, 2014, 79(3): WA13-WA21.