配電網高阻接地故障時頻特征SVM分類識別方法

張君琦 楊 帆 郭謀發

（1. 福州大學電氣工程與自動化學院，福州 350116；2. 國網南平供電公司，福建 南平 353000）

配電網系統由于深入居民區，網絡復雜，線路距離地面較近，運行時容易接觸周圍的樹枝、建筑物等[1]。配電網線路在接觸到具有高阻抗的一些表面，如碎石、瀝青、樹木、沙礫等物體時，會發生高阻接地故障。同時，如大風、雷擊等惡劣的天氣原因也會造成高阻接地故障的產生。

高阻接地故障發生時，由于過渡電阻很大，引起的電壓、電流突變量并不明顯，因此常規保護不能可靠發出動作或報警[1]。高阻接地故障一般會長時間存在，一旦數值不大的故障電流長期存在而不能被發現，將產生嚴重的后果：故障點電弧燃燒和高溫引發火災，造成電氣設備永久性損壞，且高阻接地故障多落于沙地、水泥地等，可能導致人身觸電等安全事故，因此需要對其進行快速檢測及識別分類，并采取相應措施。

高阻接地故障檢測技術過程可以分為 3個部分，包括數據獲取、信號處理與特征提取以及合適分類器的選取。

對HIF這樣的隨機性，非線性、非平穩性、不對稱性的信號，用于分析HIF信號的方式可分為4類，即時域、頻域、時間尺度域和時頻域。文獻[2]采用傅里葉變化對電流電壓進行諧波分解，提取其3次、5次諧波。時域和頻域的分解方法都會導致信號的部分信息丟失，時頻信號分解方法彌補了時域法與頻域法在信號分解中的弊端。文獻[3]采用了 S變換的方法進行信號時頻分量的提取，而目前使用較為廣泛的是小波分解的方法。文獻[4]對饋線的三相電流做離散小波變換后，提取各層的平均值及均方根值為特征量，采用貝葉斯分類器進行分類。文獻[5-8]在信號的處理上采用的也是小波分解。雖然小波分解對分析突變信號和奇異信號非常有效，但母小波的選擇會影響最終變換的效果。

近幾年來，基于機器學習的多種分類器應用于高阻接地故障的識別分類中。文獻[9]將決策樹算法引入了故障識別中。文獻[10]利用支持向量機進行高阻接地故障的識別。

LCD時頻分解方法是一種自適應分解的信號分解方法，分解效果好，適應性高。通過LCD時頻分解以及帶通濾波算法，在配電網發生故障時，構造主變低壓側電流的時頻矩陣，求取各頻帶的標準差為識別特征向量；利用支持向量機（SVM）進行高阻接地故障的分類識別。

1 高阻接地故障識別方法

1.1 配電網高阻接地故障的典型特征

自1977年以來，國內外大量實驗和研究分析普遍可以得到高阻接地故障有以下幾項典型特征[11]。

1）故障電流變化微弱

高阻接地故障常常發生于水泥、沙地、草皮等表面上，致使接地電阻較大，所產生的故障電流很小，故障點的電流可能只有系統正常運行時負荷電流的10%以下。

2）故障波形隨機性強

高阻接地故障發生時常伴隨著電弧的熄滅和重燃，并且受接地介質的隨機運動的影響，故障回路會間歇性的接通，故障電流會在某一時刻突然增大或減小，具有很強的隨機性，無法通過簡單的閾值設定來判斷故障的發生。

3）故障波形非線性畸變

故障接地點所接觸的短路介質多數等效為非線性的電阻，故障電流越小，其包含的諧波幅值會越高。

1.2 高阻接地故障識別方法

本文提出一種基于 LCD帶通濾波以及支持向量機（SVM）分類器的配電網高阻接地故障識別方法。在配電網發生高阻接地故障后，利用LCD帶通濾波算法構造主變低壓側三相電流波形的時頻矩陣，對時頻矩陣求取各子頻帶的標準差作為特征向量；同時，利用支持向量機（SVM）構造分類器，將特征向量輸入SVM分類器，實現高阻接地故障與其他相似正常工況擾動（如電容器投切、負荷投切、勵磁涌流的情況）的辨識。

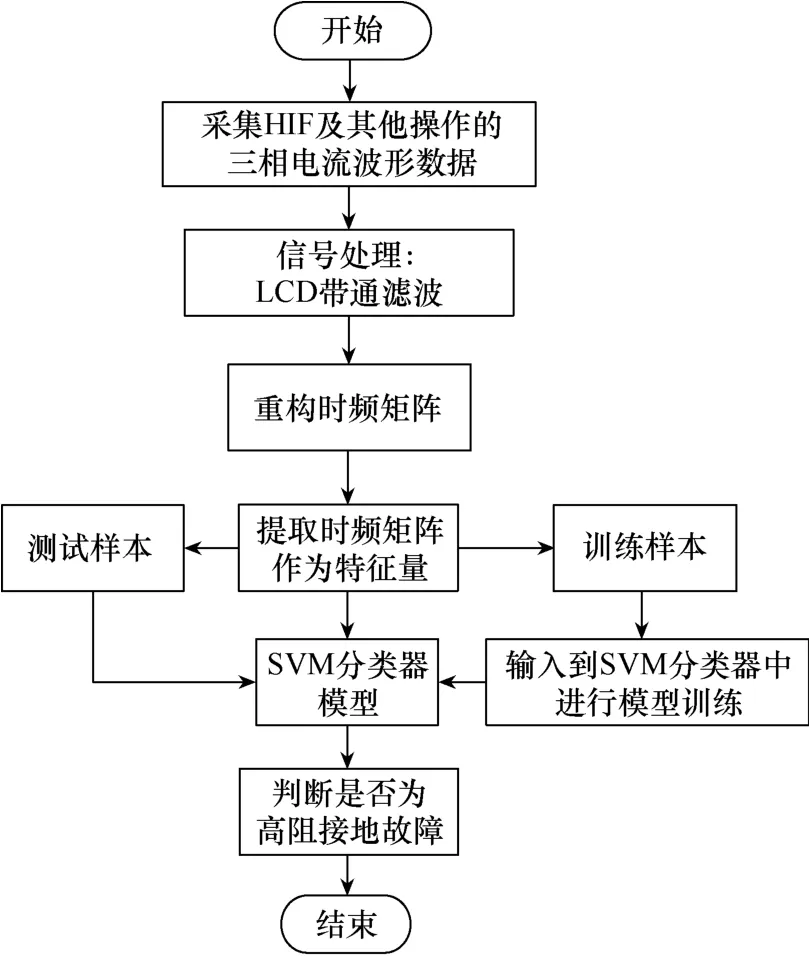
圖1 配電網高阻接地故障識別方法流程圖

1）時頻矩陣求取方法與特征量提取

局部特征尺度分解（LCD）是一種針對非平穩信號的分析方法，具有一定的自適應性，其與經驗模態分解（EMD）均是對原始信號進行自適應分解，但其在分解速度和迭代次數等方面都優于EMD[12]。

局部特征尺度分解（LCD）方法是假設一個復雜信號是由不同的內稟尺度分量（ISC）分量組成，即可以將一個波形信號分解為多個ISC分量，任兩個ISC分量之間是完全獨立的。根據所定義的ISC分量，將任意信號進行局部特征尺度分解，分解成幾個ISC分量和一個殘余項之和[13-14]。

其具體分解步驟如下。

（1）得出原始信號的所有極值點（τk,Xk），k = 1,2,… ,M ，M為極值點個數。由任意兩個相鄰的極大（或小）值點（τk,Xk）和（τk+2,Xk+2）確定的一條曲線在τk+1時的縱坐標為

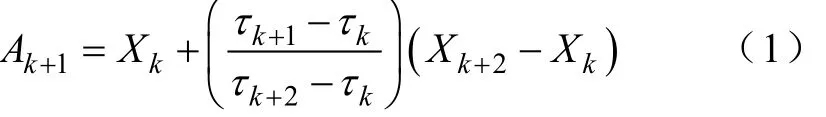
（2）根據式（1）計算出 Ak+（1k =2,3,… ,M ?1），利用（τk+1,Xk+1）與（τk+1,Ak+1）進行插值計算，得到一般 a = 0.5。

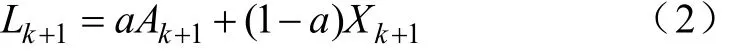
（3）對求取出的所有 L （kk =2,3,… ,M ?1）做三次樣條擬合得到均值曲線 B L1( t)。

（4）將均值曲線從原信號中分離出來，即

如果 h1( t)滿足ISC的定義，則ISC1=h1( t)，執行步驟（5）；否則，以 h1( t)為原始信號重復步驟（1）至步驟（3），直到滿足條件為止。

（5）得到剩余信號 r1( t) = x( t) ? I SC1，將其作為原始信號重復步驟（1）至（3），得到ISC2。之后，重復以上步驟，直至剩余信號單調或小于閾值時停止，則原始信號可表示為

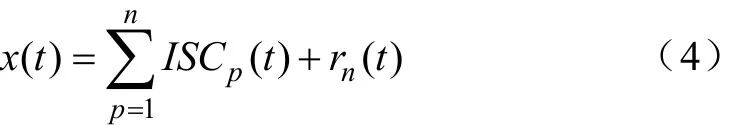
圖 2為高阻接地故障時三相電流波形，其經LCD自適應分解后，得到了一個ISC分量以及一個殘余項，得到的ISC分量如圖3所示。

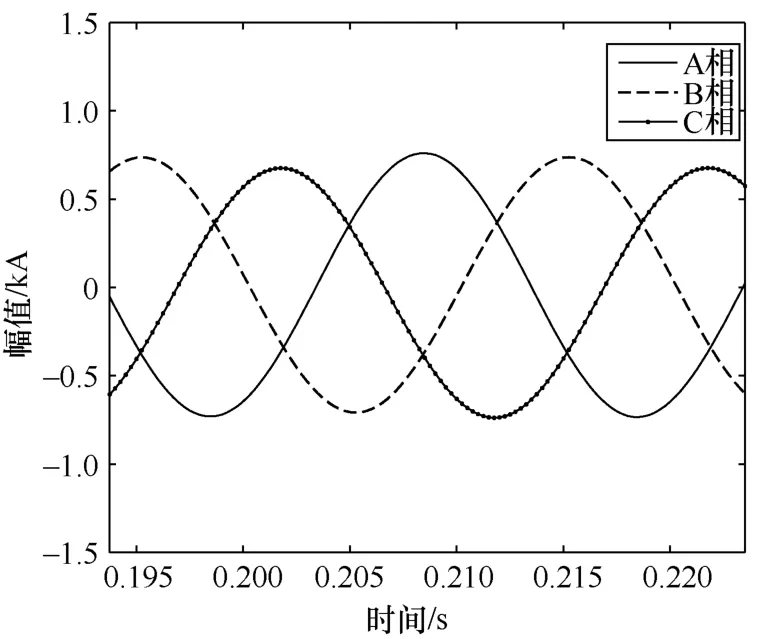
圖2高阻接地故障主變低壓側三相電流波形

圖4 所示的是電容器投切、負荷投切、勵磁涌流等正常工況擾動發生時所得到的波形，將這些波形使用相同的步驟進行數據處理以及特征量提取。

為了更直觀地表現各個故障波形在時域和頻域上的特征，通過LCD帶通濾波構造各個故障波形的時頻矩陣[15]。利用假設各個波形采樣點數均為n，故障波形經LCD帶通濾波后分解為m個子頻帶，各個子頻帶波形的數據點為ija（i=1,2,…,m；j=1,2,…,n），則可得到時頻矩陣為

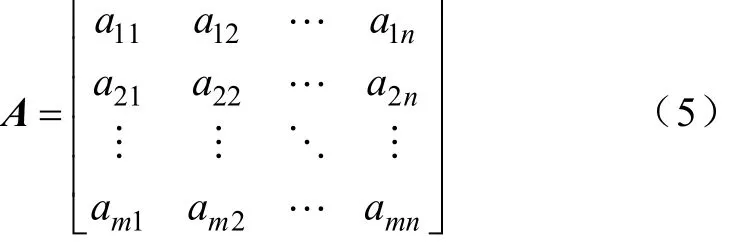
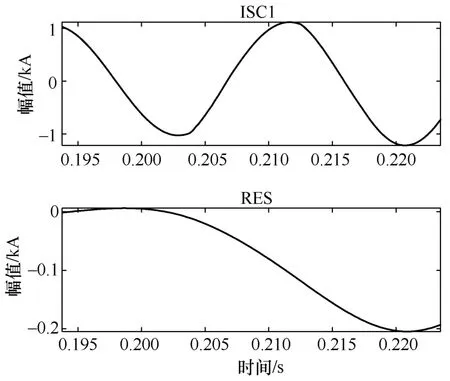
圖3 高阻接地故障ISC分量

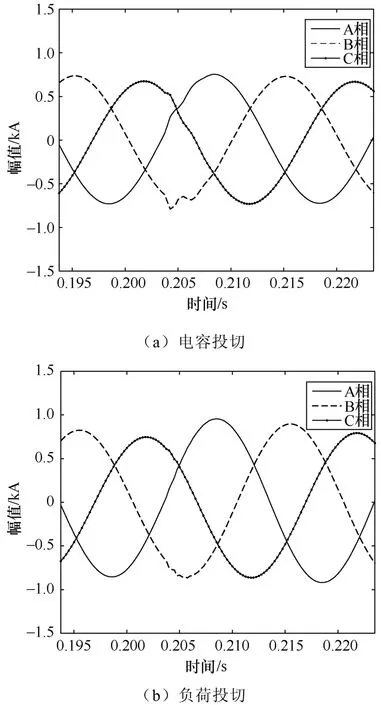
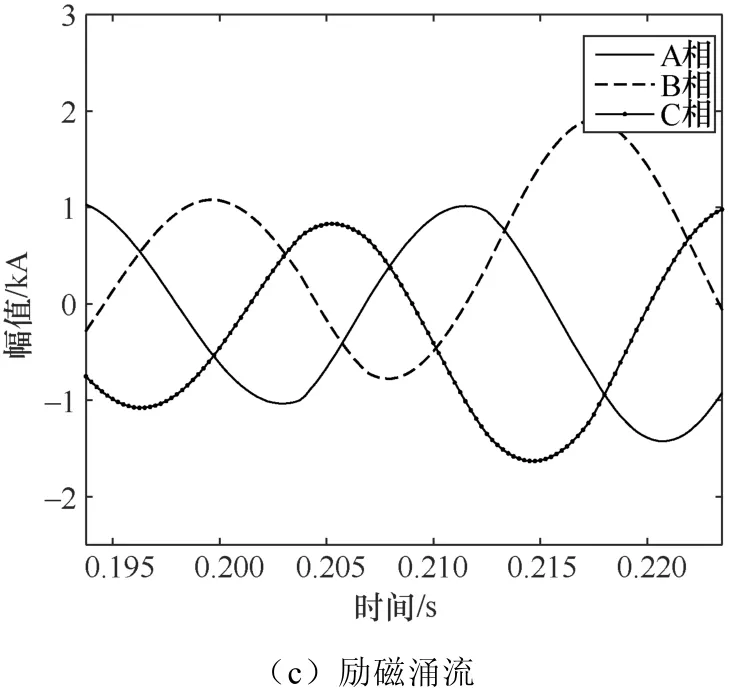
圖43 種暫態擾動的主變出線三相電流波形

其中，行表示故障波形經LCD帶通濾波后各個子頻帶的重構波形數據，列表示故障波形的采樣時刻。時頻矩陣A能夠完整地表現了故障波形在各個子頻帶上的時頻信息。

本設計中采樣頻率為 10kHz，選取的是故障前半周波與故障后一周波的三相電流波形，則采樣點數為 120n= 。最大頻率為3kHz，選取子頻帶數 5m=對瞬時頻率進行等間隔劃分，則第1個子頻帶范圍為0～600Hz，第2個子頻帶范圍為600～1200Hz，依此類推直至第5個頻帶。

針對得到的時頻矩陣求取各頻帶的標準差作為特征向量，即計算矩陣每一行的標準差，可以得到5個標準差值，因此三相電流波形可以得到15個標準差值作為輸入的特征向量。

2）SVM在配電網高阻接地故障識別中的應用

支持向量機（SVM）是一種基于統計學習理論的機器學習算法，是根據結構風險最小化原則所提出。SVM對小樣本、非線性、高維度的樣本的分類問題上效果優于其他智能技術，已被廣泛應用于電力系統故障診斷和圖像辨識等領域。為了實現高阻接地故障的識別分類問題，引入了非線性可分支持向量機[16-17]。

構建SVM分類器的主要步驟如下：

1）訓練樣本特征向量的提取。按照本文的方法提取 N個樣本的特征向量，則數據集合為D={(Xl, fl) |l = 1,2,… ,N}， fl∈ { 1,0}代表類別標識，1為高阻接地故障，0為其他運行工況過程。

為使訓練樣本具備代表性，充分計及暫態過程發生的位置、投入初相角、各參數值大小以及相別等諸多因素對識別結果的影響，在圖4的仿真平臺上進行高阻接地故障仿真，同時，在此模型上進行其他常見擾動暫態信號，如電容投切、負荷投切以及勵磁涌流等情況的仿真，獲取不同的暫態信號用于分類，得到的總訓練樣本數為1008組，樣本分布情況見表1。

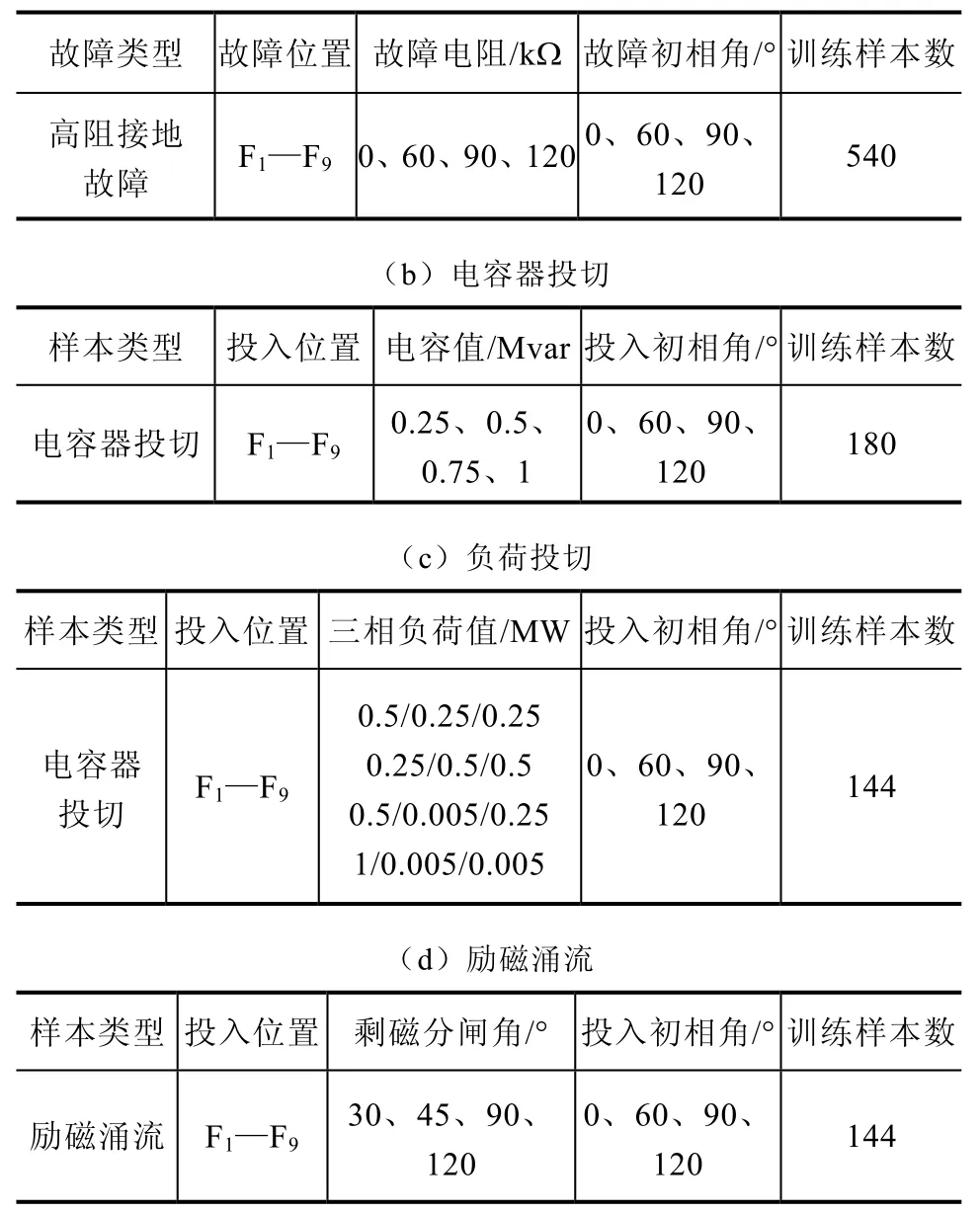
表1 訓練樣本分布情況（a）高阻接地故障

2）構建SVM分類器。根據SVM算法，針對上述的訓練樣本數據集，存在超平面 H ：ωx+b=0，其中ω為最優分類面的法向量，b為分類閾值。

3）參數選取。本文構建的是以徑向基（RBF）函數為核函數的SVM，高斯核函數表達式為

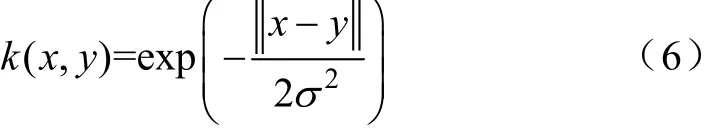
該類SVM的性能主要受2個參數影響：懲罰因子C和核函數核寬度σ，調整懲罰因子C在保證最小誤分率的同時可以產生最大的區分間隔，核函數核寬度σ越大，表示樣本在高維空間的分布越復雜。參數C與σ的數值形成一個二維向量空間，采用交叉驗證的方法進行優化。選取在各次測試中正確率最高的一組參數向量作為最優參數。經訓練及參數優化后得到的SVM分類器交叉驗證率為96.93%。

2 仿真與建模

2.1 10kV配電網模型

利用 PSCAD/EMTDC仿真軟件搭建了一個10kV配電網諧振接地模型，如圖5所示。在該配電網模型上進行各種情況的仿真實驗，獲取主變低壓側三相電流的波形數據。在配電網模型中，T1為110/10kV變壓器，其具體參數見表2。10kV側為中性點經消弧線圈接地系統，系統阻抗0.2Ω。L1是純架空線路、L2是純電纜線路、L3—L6是纜線混合線路。F1—F14為故障點。電纜線路正序參數為：R1=0.27Ω/km，C1=0.339μF/km，L1=0.255mH/km；電纜線路零序參數為：R0=2.7Ω/km，C0=0.28μF/km，L0=1.019mH/km。架空線路正序參數為：R1=0.125Ω/km，C1=0.0096μF/km，L1=1.3mH/km；架空線路零序參數為：R0=0.275Ω/km，C0=0.0054μF/km，L0=4.6mH/km。設置各線路的不同接地參數，以模擬配電系統運行時不平衡的狀態。

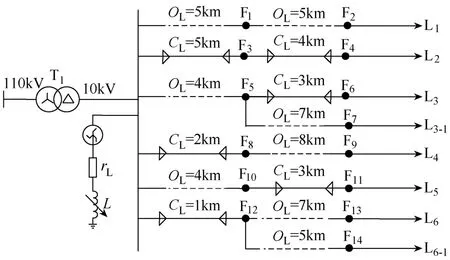
圖510 kV配電網模型

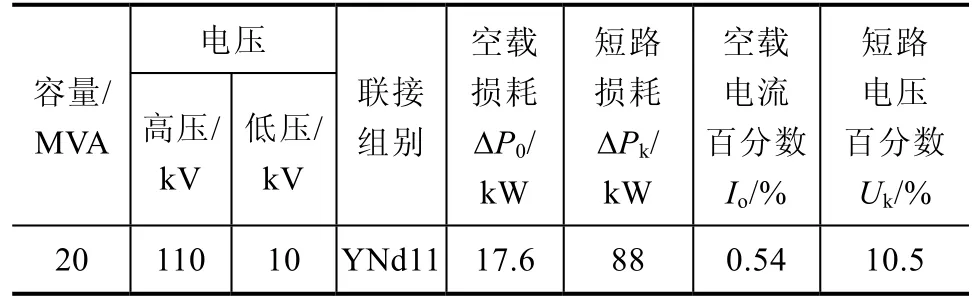
表2110 /10kV變壓器參數

2.2 高阻接地故障模型

由于高阻接地故障多數伴隨著電弧發生，因此無法采用簡單的單相接地故障模型來模擬故障。

高阻接地故障模型采用的是基于伊曼紐爾電弧的模型，模型如圖6所示，該模型由2個直流源，2個二極管以及2個可變電阻組成正負半周電流的通路[18]。2個直流源Vp，Vn模擬來自電弧的電壓，當Vph＞Vp時，電流流向大地；當 Vph＜Vn時，電流反向；當Vph在Vp和Vn之間時，電壓被Vp或Vn抵消，無電流流過；改變Vp、Vn的大小會增加故障的隨機性和消弧時間。Rp、Rn模擬的是電弧電阻，可以通過調節Rp、Rn來控制故障電流的大小。

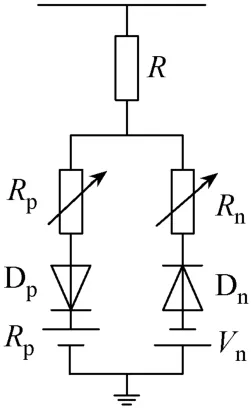
圖6 高阻接地故障模型

本模型中，直流源Vp=3.0kV，Vn=2.0kV，隨機變化為±10%；可變電阻Rp，Rn在[0,50]Ω之間，每0.05ms隨機獨立變化。在訓練及測試過程中所使用的接地電阻范圍在0.5～8kΩ之間。

2.3 其他暫態模型

配電系統中有許多正常操作與高阻接地故障有極為相似的暫態波形，比如：電容器投切、負荷投切、變壓器空載合閘所產生的勵磁涌流。因此，在仿真平臺上也對上述的3種情況進行仿真模擬。

1）電容投入。電容器的接線方式一般分為三角形和星形兩種方式。本研究采用三角形接線方式。

2）負荷投入。配電網的負荷一般是為感性負荷，因此本次設計中的投切的負荷為阻感性的三相不平衡負荷。

3）勵磁涌流。變壓器空載合閘的勵磁涌流模型的關鍵模塊為雙交流模擬變壓器剩磁。通過改變電源2的相位來模擬不同分閘角時的變壓器的剩磁。控制2個虛擬開關的切換（當BRK2斷開時BRK1合閘）來模擬不同剩磁時的變壓器勵磁涌流，并且為了防止 2個開關切換時電壓波形發生畸變，在PSCAD仿真中開關BRK2需要設置為在任何電流大小時均可打開[19]。

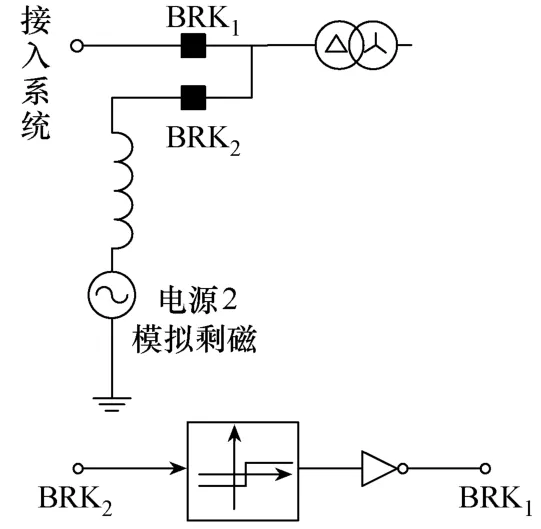
圖7 變壓器空載合閘勵磁涌流模型

2.4 識別結果

綜合考慮多個影響因素，選取不同時刻、不同位置以及不同參數值的測試樣本（總樣本容量為1172組）。根據上述步驟提取出三相電流的時頻矩陣各頻帶的標準差值作為特征向量，總識別正確率可以達到98.24%。

3 識別方法的適應性分析

3.1 適應性實驗

為了測試分類算法的可靠性和適應性，對所提出的算法進行適應性分析，考慮的情況包括：中性點接地方式改變、分布式電源接入、網絡結構變化。

1）中性點接地方式改變。為了測試識別方法是否能適應不同接地方式的系統，將仿真系統的接地方式改為中性點不接地。

2）分布式電源接入。考慮到配電網中有越來越多的分布式電源接入，故而對分布式電源接入工況的適應性也是一項十分重要的指標。在配電網軟件模型中的線路L2末端接入一個分布式電源，電源等效參數采用文獻[20]中對小水電站等效得到的參數，等效阻抗為0.02+j1.57Ω。

3）網絡結構變化。配電網的結構常常發生變化，因此考慮識別算法在不同網絡結構下的適應性，通過增加或減少線路來得到不同的配網網絡。考慮減少線路L6改變網絡結構變化。

3.2 適應性分析結果

在進行上述幾種適應性分析實驗時，在F1、F3、F5、F8、F10五處進行各情況的仿真，投入時刻為0°、60°、90°、120°，高阻接地故障中接地電阻為 0.7kΩ、1kΩ、3kΩ、5kΩ，電容投切中電容值為1Mvar，三相負載為 0.5MW/0.25MW/0.25MW，勵磁涌流中的剩磁分閘角為30°。

綜合以上幾種適應性實驗的分類測試結果見表3。

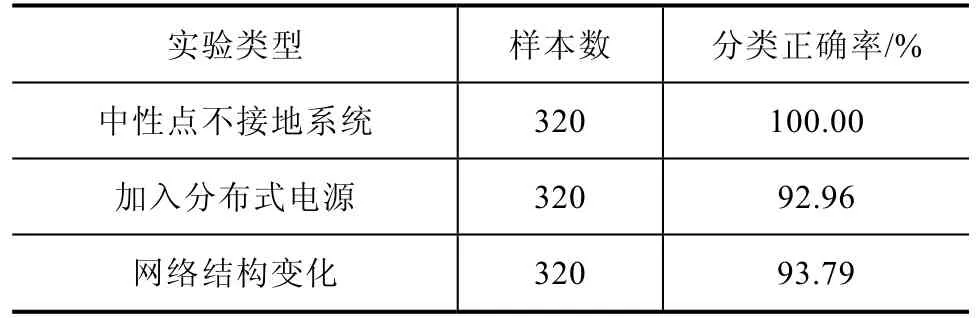
表3 適應性分析結果

由表3的實驗結果可以看出，即使中性點接地方式以及網絡結構的改變，分類算法的正確率達到90%以上。可見，分類算法的適應性較強，在不同情況下均能較好的識別高阻接地故障。

4 結論

結合波形時頻矩陣和支持向量機（SVM）提出了一種配電網高阻接地故障的識別方法，對高阻接地故障及一些運行工況進行識別。測試結果表明：

1）利用LCD帶通濾波算法構成的時頻矩陣能夠表征波形在各頻帶中的時頻特征。

2）通過支持向量機驗證了利用統計學方法提取特征向量的有效性。

3）提出的識別方法在不同的仿真狀態下均有較強的適應性，其識別正確率均可達到90%以上，能有效的用于配電網高阻接地故障的分類識別。

[1] 朱曉娟, 林圣, 張姝, 等. 基于小波能量矩的高阻接地故障檢測方法[J]. 電力自動化設備, 2016, 36(12):161-168.

[2] Sharaf A M, Wang G. High impedance fault detection using feature-pattern based relaying[C]//Transmission and Distribution Conference and Exposition, 2003:222-226.

[3] Mishra M, Routray P, Rout P. A universal high impedance fault detection technique for distribution system using S-Transform and pattern recognition[J].Technology and Economics of Smart Grids and Sustainable Energy, 2016, 1(1): 9.

[4] Sedighi A R, Haghifam M R, Malik O P, et al. High impedance fault detection based on wavelet transform and statistical pattern recognition[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2414-2421.

[5] Michalik M, Lukowicz M, Rebizant W, et al.Verification of the wavelet-based HIF detecting algorithm performance in solidly grounded MV networks[J]. IEEE Transactions on Power Delivery,2007, 22(4): 2057-2064.

[6] Costa F B, Souza B A, Brito N, et al. Real-Time detection of transients induced by High-Impedance faults based on the boundary wavelet transform[J].IEEE Transactions on Industry Applications, 2015,51(6, 2): 5312-5323.

[7] Sedighi A R, Haghifam M R, Malik O P. Soft computing applications in high impedance fault detection in distribution systems[J]. Electric Power Systems Research, 2005, 76(1/3): 136-144.

[8] 陳民鈾, 黃永, 瞿進乾. 配電網線路高阻故障識別方法[J]. 重慶大學學報, 2013, 36(9): 83-88.

[9] Samantaray S R. Ensemble decision trees for high impedance fault detection in power distribution network[J]. International Journal of Electrical Power &Energy Systems, 2012, 43(1): 1048-1055.

[10] 鄭星炯. 基于支持向量機的配電線路高阻接地故障檢測方法[J]. 電子設計工程, 2015, 23(14): 122-125.[11] 耿建昭, 王賓, 董新洲, 等. 中性點有效接地配電網高阻接地故障特征分析及檢測[J]. 電力系統自動化,2013, 37(16): 85-91.

[12] 郭謀發, 游林旭, 洪翠, 等. 基于 LCD-Hilbert譜奇異值和多級支持向量機的配電網故障識別方法[J].高電壓技術, 2017(4): 1239-1247.

[13] 孫一航, 武建文, 廉世軍, 等. 結合經驗模態分解能量總量法的斷路器振動信號特征向量提取[J]. 電工技術學報, 2014, 29(3): 228-236.

[14] 蔡晉, 林榛, 高偉, 等. 基于 HHT及信號注入的配電網諧振與單相接地故障識別[J]. 電氣技術, 2015,16(12): 31-35, 51.

[15] 郭謀發, 劉世丹, 楊耿杰. 采用Hilbert譜帶通濾波和暫態波形識別的諧振接地系統故障選線新方法[J].電工電能新技術, 2013, 32(3): 67-74.

[16] 程序, 關永剛, 張文鵬, 等. 基于因子分析和支持向量機算法的高壓斷路器機械故障診斷方法[J]. 電工技術學報, 2014, 29(7): 209-215.

[17] 魏曉瑩, 宋仕江, 郭謀發, 等. 基于振動信號二維特征向量的配變鐵心故障診斷[J]. 電氣技術, 2016,17(1): 16-21.

[18] Gautam S, Brahma S M. Detection of high impedance fault in power distribution systems using mathematical morphology[J]. IEEE Transactions on Power Systems,2013, 28(2): 1226-1234.

[19] 劉超, 劉健, 張志華, 等. 配電網勵磁涌流及其概率分布的分析與探討[J]. 電力系統自動化, 2017, 41(4):170-175.

[20] 張元勝, 李欣然, 肖園園, 等. 含小水電配網負荷模型實用化方法[J]. 電工電能新技術, 2012, 31(4):83-87.