斜橢圓數控車加工規律性探究
吳鳳霞
(蘇州市高等職業技術學校,江蘇 蘇州 215111)
伴隨工程技術的不斷進步,當前在數控車床領域使用宏程序進行加工處理,并保持其位置始終不傾斜的曲線旋轉面技術日漸成熟,并被應用到各類數控車床生產加工工作中。旋轉面技術所涵蓋的公式曲線有橢圓、拋物線等類別,但此類曲線存在一定的實踐運用問題:當其曲線經過一定時間或角度的旋轉運動后,相應的曲線公式就會變得傾斜,如圖1所示橢圓曲線經過轉動后逐漸變為斜橢圓曲線,如何有效解決這一傾斜問題,就需要相應的技術人員探討其斜橢圓加工的規律,以此找出相應的解決、加工措施。
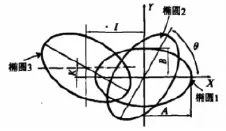
圖1 橢圓曲線旋轉、傾斜為斜橢圓曲線的坐標系變化圖
1 橢圓曲線變為斜橢圓曲線的過程探究
首先將橢圓曲線經過坐標點的旋轉以及相應的平移運動,就能得到其傾斜后的斜橢圓曲線,以此方便對其變換過程做具體、細致的分析研究。
(1)公式曲線在坐標位置上的改變。公式曲線的坐標體系中任意一個點的旋轉變換,均可經由一個旋轉軸和一個旋轉角度來確定。為了便于后續的運算檢驗工作,首先將橢圓曲線一點的旋轉軸作為其坐標體系中的坐標軸,如圖2所示點(x,y)就是環繞著Z軸,在旋轉θ度角后停留于P′(x′,y′)位置。
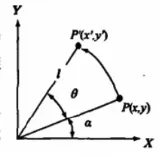
圖2 某一點在曲線坐標系中的旋轉圖
因此該點的坐標旋轉變化的公式可總結為:
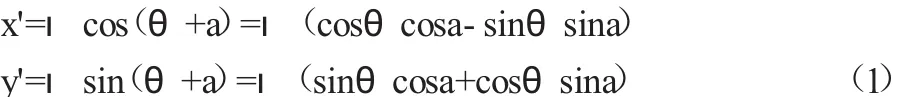

其中把公式(3)變為為矩陣方式即為:
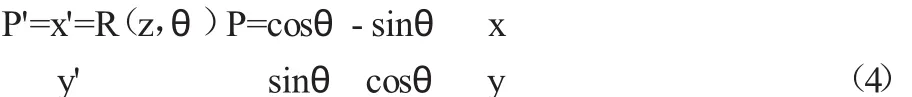
此時矩陣R(z,θ)就是環繞著Z軸進行旋轉變化的矩陣方程,以此方法再得出 R(x,θ)與 R(y,θ)兩個矩陣,進而構建其三維空間下的旋轉變化坐標矩陣體系,其中共含有九個元素,分別為:
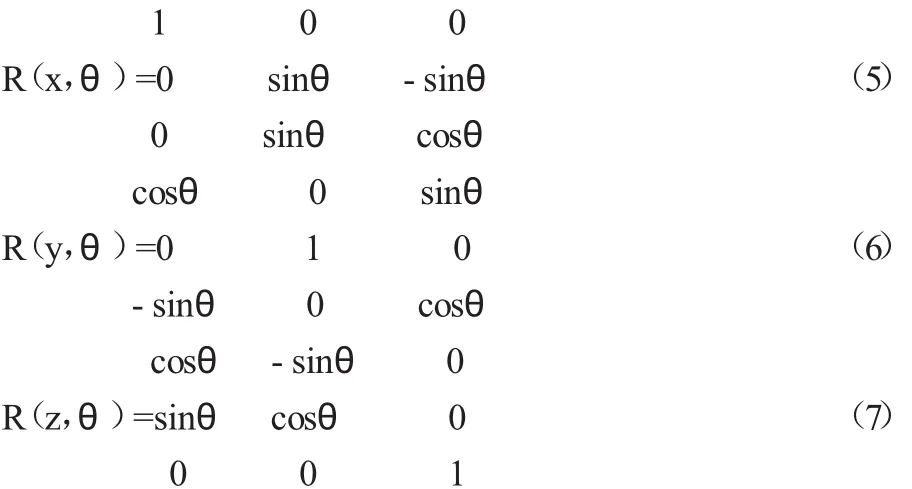
(2)斜橢圓曲線方程的研究確立。依據圖1所示,可以發現圖中的橢圓1的表達方程式,可以表述為以下兩種形式:

或是X=Acosw

之后依照圖1表示,在橢圓1沿著Z軸逆時針旋轉θ角度后就可得到橢圓2,依據公式(9)將其橢圓方程式做相應的變化可得到:

進而得出橢圓2在原本坐標系位置中的方程式:

之后再將橢圓2進行平移運動最終得到橢圓3,即斜橢圓的曲線方程式:
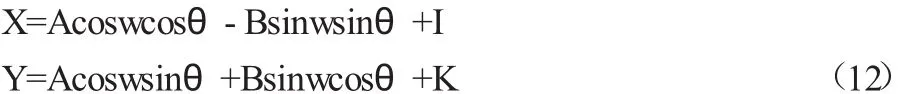
2 斜橢圓曲線中各變量之間的聯系探究
斜橢圓曲線中轉角變量w與圓心角λ是探究其形成規律的重要參數,依照公式(9)可以發現如果能掌握A、B的具體數值,通過相應轉角變量w的變換(在0°~360°之間變動),就能依照圖形繪畫的方法,將相應橢圓圖描繪出來,依據圖3所顯示的內容,圖中外部大圓的半徑即為A,而內部小圓的半徑是B,橢圓中任意一個點與圓心之間的連線,和水平坐標右軸線之間的夾角即為圓心角λ。
從關系中可以研究發現轉角變量w與圓心角λ之間存在聯系與規律為:
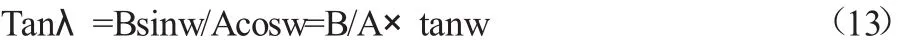
而在數控機床的實際零件加工作業中,依據其圖樣可較為便利地求得其橢圓圓心角λ,相應就能依照圓心角數值與公式(13)求得該橢圓的轉角變量w。
3 斜橢圓數控加工宏程序的設計、規劃思路
前文所探討的公式(12)是橢圓在坐標體系中的通常方程式,相應式子中其余參數均為固定常數,僅有轉角變量w是不確定的,當實際加工僅處理橢圓的局部輪廓時,就只需相應測算橢圓在起始位置的轉角變量w1,以及相應的終點位置的轉角變量w2,通過運算出轉角變量在w1到w2之間的角度差,進而依照公式(12)求出需要進行加工的橢圓輪廓的點的坐標位置。
斜橢圓數控加工的具體宏程序規劃流程和步驟中δ指的是轉角的增量角,其數值愈大,則逼近橢圓輪廓的效果愈差,并且方程式所用的坐標軸為XZ坐標體系,其與公式(12)中的XY坐標體系存在偏差,因此具體的斜橢圓數控加工處理規律的運用方法,將在后文的加工示例中做證明。
4 斜橢圓數控加工規律運用示例及其研究
數控車床加工的零件如圖3所示,其為直徑50mm,長度80mm的鋁合金零件。
(1)坐標系之間的整合應用。通過觀察圖1與圖3之間的橢圓坐標體系圖,可以了解到圖3中橢圓坐標所用的X軸即為圖1中橢圓坐標所用的Y軸,而圖3中坐標系中的Z軸即為圖1坐標體系中的X軸,由此就可以通過各個坐標軸之間的對等銜接,將斜橢圓的曲線方程式從公式(12)變換為零件加工所需的公式(14):
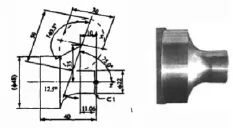
圖3 加工零件的實物圖與坐標變換圖
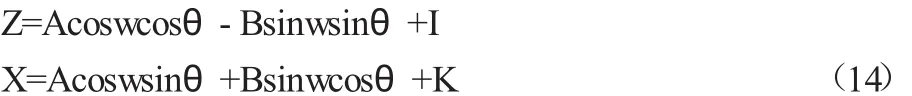
(2)具體斜橢圓方程式的求解運算。通過對圖3的坐標圖研究可以知道 A=25,B=15,θ 為 75°,而 I=-10,K=35,而圓心角λ1為192.5°,λ2則為140.3°。
將其參數套入公式(13)中,就可求得橢圓的起始位置轉角變量w1為200.2°,而終點位置轉角變量w2為125.8°,由此斜橢圓曲線的具體方程式就可列為:
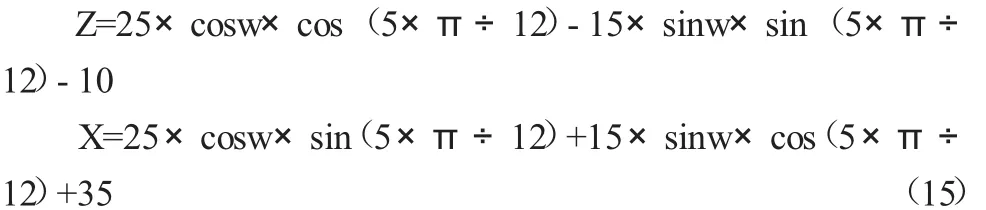
之后經由對轉角變量w從w1變換到w2,以此得出相應轉角增量角,使之逼近橢圓輪廓曲線,再依照公式(15)進行相應斜橢圓曲線上各點坐標的具體求解運算。
5 結語
通過上述斜橢圓變換、求解規律的研究掌握,相應斜橢圓的數控加工工作就能迎刃而解,因此值得技術人員對其曲線方程規律做進一步的理解與運用,以優化數控機床的加工處理效率。
[1]韋玉秋.斜橢圓數控車加工問題探討[J].科技致富向導,2012,(29):398-399.
[2]雒銳.斜橢圓數控車加工方法探究[J].電子制作,2013,(21):34+3.
[3]趙薇,薛明.《基于德國“雙元制”工作過程的數控車工課程改革》課題報告相關論文之三:斜橢圓類零件數控車削加工方法研究[J].國土資源高等職業教育研究,2016,(1):28-31+39.

