基于PSO算法的離散制造車間物料供應路徑優(yōu)化*
姚 勇,李少波,張成龍
(貴州大學 a.機械工程學院;b.大數據與信息工程學院,貴陽 550025)
0 引言
在實際的送料過程中,送料車根據生產計劃部門的物料計劃對加工車間的機床進行送料且計劃中的每個機床都至少到達一次。于是在忽略了各種偶然因素之后,加工車間送料問題可大致歸結為一個旅行商問題(TSP問題)。
目前,為求解高復雜度TSP問題主要采用遺傳算法[2]、模擬退火算法[3]、蟻群算法[4]、粒子群算法等啟發(fā)式算法。鑒于粒子群算法具有個體數目少、搜索能力快、運算簡單等特點,成為了近年來求解TSP問題的一個熱門方法。而為了克服粒子群算法在離散問題中速度難以表達,易早熟收斂等問題。學者們從以下幾個方面對粒子群算法提出改進。第一類是重新定義粒子群算法的運算符號和規(guī)則,例如文獻[5]采用的離散粒子群算法,文獻[6]提出的基于交換子交換序的粒子群算法。第二類是通過與遺傳算法、退火算法、蟻群算法相融合[1-3],借助交叉、變異等方法來實現改進。雖然上述方法在具體應用中均取得了一定的效果,但是對新型改進方法的探索仍然是一個研究熱點。
本文基于交換子與交換序的概念,針對現有算法求解效率不佳的問題,提出一種慣性權重非線性遞減,加速因子隨慣性權重進行動態(tài)調整的改進策略來提高算法的全局搜索能力,同時克服早熟收斂問題。通過車間模擬實驗的測試驗證了該算法能對車間送料路徑優(yōu)化起到良好的作用。
1 相關問題描述及物料供應數學模型
經典旅行商問題描述如下:給定一系列城市和兩兩城市之間的距離,求解訪問每一座城市一次并回到起始城市的最短回路。我們首先將車間各加工機床與倉庫所構成的網絡圖轉換為帶權完全無向圖。則其圖論描述為:G=(V,A),V表示為圖中結點的集合,一個結點代表加工車間被送料的機床,A表示圖中弧的集合,已知各結點間的連接距離,找一個權值最小的Hamilton回路。即遍歷所有頂點一次且僅一次的最短回路,設dij為加工機床i與j之間的距離,即弧(i,j)長度,引入決策變量:

(1)
則其目標函數為:
(2)
TSP問題描述很容易,但由于該問題的可行解是所有頂點的全排列,隨著頂點數的增加,會產生組合爆炸。求解相當困難,本文尋求通過對基本PSO算法進行改造來應用于求解TSP問題。
2 標準粒子群優(yōu)化模型
基本粒子群算法是基于種群的全局搜索策略,將每一個可能產生的解表述為群中的一個粒子,通過粒子間的合作與競爭,在復雜空間中找到最優(yōu)解,之后為了使粒子群保持運動的慣性,在保證具有全局搜索能力的同時擴展其搜索的空間,使其有能力搜索新的區(qū)域。Eberhart和shi在速度更新方程中引入慣性權重ω的概念[7],從而得到了標準粒子群優(yōu)化算法。算法中所有的粒子都有一個被優(yōu)化函數決定的適應值,并且同時具有速度與位置兩個屬性。每一次迭代過程中粒子通過追蹤個體極值Pi與全局極值Pg來更新自己。個體極值表示粒子本身所找到的最優(yōu)解。全局極值表示整個種群目前的最優(yōu)解。粒子i的信息用d維向量表示,位置表示為Xi=(Xi1,…,Xid),速度表示為Vi=(Vi1,…,Vid)其中Vid(t)是粒子i在第t次迭代中第d維速度,Xid(t)是粒子i在第t次迭代中d維當前位置。粒子通過公式(3)、(4)對速度與位置進行動態(tài)調整。
總之,本研究發(fā)現PET/CT聯合HRCT可以提高對不同大小SPN診斷的準確率,尤其是對于直徑≥2cm的SPN,準確率達到90.9%。對于直徑<2cm的SPN,為提高診斷的準確率,有必要臨床醫(yī)生、CT室、PET/CT多學科的討論,才能避免不必要的誤診及漏診。
Vi(t+1)=ω·Vi(t)+c1r1(Pid(t)-Xid(t))+
c2r2(Pid(t)-Xid(t))
(3)
Xid(t+1)=Xid(t)+Vid(t+1)
(4)
c1,c2是加速度系數,其作用是表示將每個粒子移向兩極值位置的統計加速項權重。取值為(0,2)之間的隨機數。r1,r2是(0,1)上的隨機數,ω為慣性權重,用來控制前面速度對后面速度的影響ω取值較大時,粒子具有較好的全局搜索能力,ω取值較小時則具有較好的局部搜索能力。在基本PSO算法中,一般設定c1=c2=2,ω=1。但在此情況下粒子的軌跡會出現發(fā)散的現象所以需要限制每一個粒子的每一維速度范圍[Vmin,Vmax],以此來限定粒子的運動軌跡,當Vt>Vmax時,Vt=Vmax,當Vt 由于TSP問題為一個離散問題,而在基本PSO算法中速度向量難以表達離散域問題,因此要解決TSP問題需要對基本PSO算法中運算符號和規(guī)則進行重新定義,文獻[6]通過引入交換子和交換序的概念,對PSO算法進行了改造。使其能應用于求解TSP問題中。其重新構造速度-位置公式如下: Vi(t+1)=ω·Vi(t)+α(Pid(t)-Xid(t))+ (5) Xid(t+1)=Xid(t)+Vid(t+1) (6) 式中,α(Pid(t)-Xid(t))表示粒子與個體極值的交換序以概率α保留,β(Pgd(t)-Xid(t))表示粒子與全局極值的交換序以概率β保留,α,β取值為(0,1),反應了個體極值和全局極值對粒子的影響程度。 文獻[6]引入交換子的方式來解決TSP問題。該算法設置100個粒子,并迭代2000次得到14個點的最優(yōu)解。擴展了PSO算法在離散條件下的應用。但是該算法的全局搜索能力并不強,易于產生早熟收斂的情況,同時沒有考慮粒子的慣性權重,這樣隨著進化的進行,算法性能會急劇惡化,使算法的求解能力大大衰減。文獻[9]在此基礎上提出了一種基于交換序的改進自組織PSO算法,利用自組織臨界性理論對自組織慣性權重和自組織加速系數進行重新設置,并引入變異等策略來提高算法的優(yōu)越性。其自組織慣性權重并未采用常規(guī)的(0.9,0.4)上線性遞減的方式,而是按自組織臨界系統的冪分布規(guī)律進行變化。將慣性權重的變換分為兩個階段,定義如下: (7) (8) iter為當前迭代次數,Maxiter為最大迭代次數,ωstart和ωend分別為初始和終止的慣性權重。第一階段中通過公式(1)延緩慣性權重的減小趨勢,從而促使粒子擴大搜索區(qū)域,減小陷入局部最優(yōu)解的可能。第二階段中通過公式(2)使慣性權重快速下降,促使粒子對局部區(qū)域進行精細搜索。自組織加速系數同樣按照自組織臨界系統的冪律分布規(guī)律進行如下定義: (1)α=Cmax,β=Cmin (2)α=Cmin,β=Cmax α=c1r1,β=c2r2,Cmax,Cmin為不相等的常數。 這種方法較基本PSO而言擴大了粒子搜索區(qū)域,有效的克服了算法的早熟收斂問題,提升了算法的性能,但是此方法中慣性權重調整策略與加速因子的調整策略相互脫離,一定程度上削弱了算法進化過程中的統一性,不利于算法優(yōu)化搜索。 因此,為了能擴大粒子搜索區(qū)域,避免陷入局部最優(yōu)解,克服早熟收斂問題。同時盡可能的讓慣性權重與加速因子在進化過程中保持統一性,進一步優(yōu)化算法。提出一種慣性權重改進方法,此方法參考文獻[9]所提出的基于交換序的改進自組織PSO算法并結合慣性權重ω在(0.9,0.4)線性遞減的方法,得出了一種慣性權重ω非線性遞減的調整策略。該策略首先將慣性權重ω初始化為0.9,以保證算法在初期具有較強的全局搜索能力,再利用非線性遞減的迭代關系式來減緩慣性權重ω在前期的下降速度,以此來開發(fā)更多的搜索區(qū)域,規(guī)避早熟收斂問題,改進的慣性權重表達式如下: (9) 同時為了盡可能的讓慣性權重與加速因子在進化過程中保持統一的進化性,進一步優(yōu)化算法,加速因子需要與慣性權重ω在迭代過程中非線性變化的特點相互匹配。因此本算法提出一組加速因子調整式: (10) 通過該式構建c、ω的聯系,使c、ω呈非線性函數關系。并借鑒已有的加速因子調整策略確定系數組合[10]。加速系數α=c1r1,β=c2r2;α、β為[0,1]上隨機數。 基于交換序的改進PSO算法求解TSP的流程如圖1所示。 圖1 改進粒子群算法流程 為了模擬加工車間機床、送料倉庫的布局情況,本實驗采用將車間中機床、送料倉庫位置坐標化的方式劃為各坐標點,同時將實驗空間設置為30m×60m的長方形區(qū)域,并以橫縱坐標劃分為300×600的單位網格。然后將各節(jié)點布置于單位網格中,并在節(jié)點位置裝上傳感器進行位置感知。 實驗運行平臺是采用Matlab軟件,針對車間送料路徑優(yōu)化問題,對文獻所采用的基于交換序的PSO算法,基于交換序的慣性權重線性遞減PSO算法以及本文所設計的基于交換序的改進PSO算法各做50次獨立仿真實驗,并進行對比。其參數設置見表1。 表1 算法參數設置 3種算法的仿真實驗結果如表2所示。 表2 實驗結果對比 對比表2中數據可發(fā)現改進后的PSO算法其平均解與最優(yōu)解均優(yōu)于其余兩種算法。 3種算法的收斂曲線如圖2所示。 圖2 路徑優(yōu)化曲線對比 通過觀察收斂曲線圖發(fā)現本文所設計的改進PSO算法迭代到34代左右適應度函數趨于穩(wěn)定得到全局最優(yōu)解337.5447,而其余兩種算法則分別迭代到43與47代才進行收斂。這表明基于交換序的基本PSO算法和 基于交換序的慣性權重線性遞減PSO算法(LDW-PSO)的整體收斂過程緩慢,全局尋優(yōu)效果不理想,而本文改進的PSO算法在收斂速度上較前兩種方法有明顯的優(yōu)勢,同時在搜索最優(yōu)解的能力上也得到了增強,可以大幅縮短物流供應路徑,總的來說改進后的PSO算法體現出了良好的優(yōu)化性能。 本文針對加工車間送料路徑優(yōu)化進行了研究,通過構建實驗環(huán)境對車間現場場景進行了模擬,建立了TSP模型。并基于交換子和交換序的概念設計了一種慣性權重非線性遞減,同時加速因子隨慣性權重的改變而調整的PSO算法來求解該問題。通過仿真實驗與其余兩種基于交換序的算法進行對比,結果表明本文所設計的算法具有更好的全局搜索能力和收斂結果。說明本算法在解決車間送料路徑優(yōu)化問題具有更好的優(yōu)越性。 [參考文獻] [1] 賀長鵬,鄭宇,王麗亞,等. 面向離散制造過程的RFID應用研究綜述[J]. 計算機集成制造系統,2014,20(5):1160-1170. [2] 沈繼紅,王侃. 求解旅行商問題的混合粒子群優(yōu)化算法[J]. 智能系統學報,2012,7(2):174-182. [3] 易正俊,李勇霞,易校石. 自適應蟻群算法求解最短路徑和TSP問題[J]. 計算機技術與發(fā)展,2016(12):1-5. [4] 孫凱,吳紅星,王浩,等. 蟻群與粒子群混合算法求解TSP問題[J]. 計算機工程與應用,2012,48(34):60-63. [5] Li Y, Jiao L, Shang R, et al. Dynamic-context cooperative quantum-behaved particle swarm optimization based on multilevel thresholding applied to medical image segmentation[J]. Information Sciences, 2015, 294:408-422. [6] Fan T E, Liu T D, Zheng J W, et al. Structural optimization of Pt-Pd-Au trimetallic nanoparticles by discrete particle swarm algorithms[J]. Journal of Materials Science,2015, 50(9):3308-3319. [7] Kennedy J, Eberhart R. Particle swarm optimization[C]//Neural Networks, IEEE International Conference on. IEEE, 1995, 4: 1942-1948. [8] Shi Y, Eberhart R. A modified particle swarm optimizer[C]//Evolutionary Computation Proceedings, 1998. IEEE World Congress on Computational Intelligence, The 1998 IEEE International Conference on. IEEE, 1998: 69-73. [9] 孫晶晶,雷秀娟. 求解TSP的改進自組織PSO算法 [J]. 計算機工程與應用,2009,45(31):30-33. [10] 趙遠東,方正華.帶有權重函數學習因子的粒子群算法[J]. 計算機應用,2013,33(8):2265-2268. (編輯李秀敏)3 基于交換序的改進PSO求解TSP
3.1 求解TSP的基本PSO算法
β(Pid(t)-Xid(t))3.2 求解TSP的改進自組織PSO算法
3.3 算法改進
3.4 改進算法流程
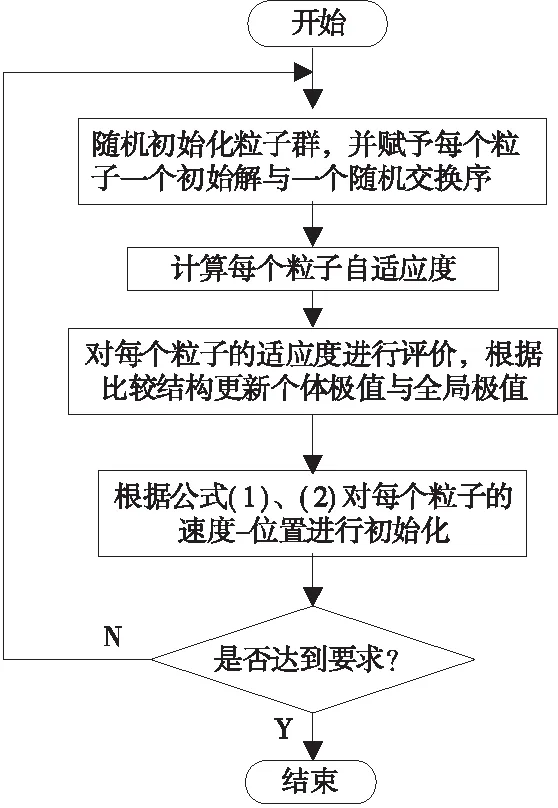
4 算法驗證
4.1 實驗環(huán)境

4.2 結果分析
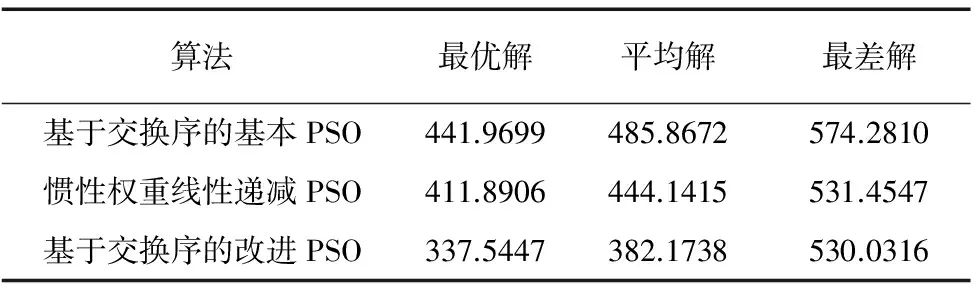
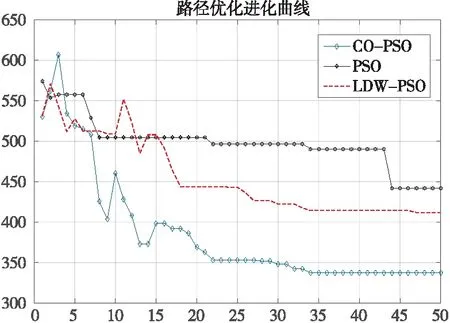
5 結論

