基于相空間重構和SVR的磨煤機故障預測研究
李德忠, 楊 柳, 胡 蓉, 任資龍, 謝小鵬, 向春波
(湖南大唐先一科技有限公司, 長沙 410007)
電站磨煤機作為鍋爐燃燒制粉系統的核心設備,其工作狀況對整個電廠系統運行的安全和經濟性具有重要的影響。在火力發電機組等效非計劃停運的所有影響因素中,磨煤機故障是主要原因之一,其故障直接影響了鍋爐機組運行穩定性、燃燒經濟性和機組出力。因此,研究磨煤機的故障診斷具有重要意義[1]。
由于火電廠磨煤機運行環境的復雜性,磨煤機的故障過程中存在著不確定性:同一故障類型表現為多種不同的故障征兆;往往不同故障類型也可能產生不同的故障征兆;不同故障征兆之間往往也存在相互關聯的關系。傳統的故障診斷方法往往很難取得理想的效果[2]。
近年來,在機器學習領域中備受矚目的支持向量回歸機(SVR)在許多領域得到了成功的應用,顯示出巨大的優越性:SVR計算的復雜度與訓練樣本變量的維數無關,能有效解決高維問題。目前廣泛使用的統計故障診斷方法包括主元分析法(PCA)、Fisher判別分析法(FDA)和獨立成分分析法(ICA)[3]。這些方法都是線性降維方法,即假設變量之間滿足線性相關關系,可通過降維和提取獨立變量來實現故障診斷;但對于磨煤機這種復雜過程,變量之間往往呈現出強耦合性和非線性關系,需采用非線性方法對磨煤機進行故障診斷[4-6]。因此,筆者采用SVR對火電廠數據進行預測。
1 預測模型
1.1 標準化處理
采用標準分數對數據進行處理,可以反映一個數據距離平均數的相對標準距離,公式如下:
(1)
式中:xij為第i條數據的第j個測試特征。
通過式(1)對數據進行標準化之后消除了量綱對數據的影響,原始數據低于平均值的時候為負數,高于平均值的時候為正數。標準化后的每一列數據的平均值為0,方差為1,而且近似服從正態分布。
1.2 基于頻率分布的一階向前差分去噪法
因為數據的差分值反映了數據的波動情況,筆者研究了設備各個指標的一階向前差分絕對值的頻率直方分布圖,發現差分絕對值小的部分頻率高,差分絕對值大的地方頻率卻很低, 因此差分絕對值比較大的部分所對應的數據更容易是異常數據。算法的基本思想是:
ci=xi+1-xi
(2)
di=|xi+1-xi|,i=1,…,n-1
(3)
式中:xi為第i條測試數據。

這種方法既可以找出孤立異常點還可以找出連續s個點以內的異常段,去掉的異常點用線性插值補全。
(3) 線性插值補全。
設去除的異常點為xi+1,xi+2,…,xi+s(s≥1),則由線性插值法得出去除的異常點補全后對應的點為:
(4)
1.3 SVR模型
SVR采用結構風險最小化原則,通過適當的非線性變換將輸入空間變換到一個高維特征空間,把在這個特征空間中尋找線性回歸最優超平面歸結為求解凸規劃問題,并求得全局最優解。SVR具有很好的泛化能力。
在SVR中,通常采用如下的ε不敏感損失函數,即
(5)
式中:f(x)為學習函數;(x,y)為訓練樣本;ε為擬合精度。
SVR的目標是尋找一個函數f(x)=ωTφ(x)+b(φ(x)為x到高維空間的非線性映射函數;ω為學習函數的廣義參數;b為分類閾值),使得它與所有訓練點的實際輸出yi的背離盡可能不超過ε,同時函數盡可能平坦。當誤差小于ε時,對其不予考慮,只考慮大于ε的誤差,多出的誤差通常用松弛因子ζi和ζi*表示。
給定訓練樣本(xi,yi)(i=1,2,…,l),其中xi∈Rm,yi∈R。根據結構風險最小化準則,SVR模型的優化目標為:
約束條件為:
式中:C為用于控制對超出ε的樣本的懲罰程度。
SVR模型的一個重要概念是核函數,由Mercer定理可得,核函數K(xi,xj)和φ(x)滿足:
K(xi,xj)=φ(xi)·φ(xj)
(6)
原始優化問題可以轉化為對偶問題:
約束條件為:
對應的KKT(Karush-Kuhn-Tucker)條件為:
當所有的拉格朗日算子αi和αi*滿足KKT條件時,解是最優的。
由KKT條件可以看出:當αi=0且αi*=0時,訓練點(xi,yi)是位于ε帶子區域(f(x)±ε)之內(包括邊界);當0<αi 求出αi和αi*(i=1,…,l)后,偏置項b的求取方法為:當0<αi 通過SVR模型可得到回歸函數如下: (7) 式中:βi為系數,βi=αi-αi*(i=1,…,l)。 訓練樣本數據采集于某電廠320 MW機組磨煤機的實際生產過程。輸入參數為磨煤機的電動機電流、潤滑油溫度、油位變化、減速潤滑油溫、油箱油溫、左側軸承溫度1、左側軸承溫度2、右側軸承溫度1、右側軸承溫度2、油箱油位、小牙輪軸承溫度1和小牙輪軸承溫度2共12個參數。選取一年的數據作為試驗數據,共8 000。 實際上數據的采集往往不完整,導致數據缺失的因素有很多,例如傳感器故障、通信線路及人為等因素都會導致一些數據的不完整[5]。采用一階向前差分去噪法對訓練樣本進行了異常數據剔除和缺失數據修補。圖1為樣本數據中磨煤機油箱油溫的數據剔除情況。 圖1 磨煤機油箱油溫的數據異常點 12個指標的數據剔除情況見表1。筆者為了消除量綱對數據的影響,避免個別特殊變量在故障診斷中占主要地位,對原始數據進行了標準化處理。 表1 訓練樣本數據中各指標中異常數據的個數 假設某一設備的訓練樣本是M維多變量時間序列{x1,x2,…,xN},xi=(x1i,x2i,…,xMi),N表示樣本個數。根據時間延遲的思想,多變量時間序列延遲相空間重構的相點為: (8) (9) 映射fi即為前面所敘述的根據SVR所得出的預測函數。 為了驗證相空間重構與SVR模型磨煤機故障預測的性能,研究通過在Matlab平臺上的仿真試驗對所提的方法進行評估。文獻[7]認為徑向基函數在處理非線性樣本時比線性函數好,而多項式核函數因其參數較多,且當其階次較高時會導致數值計算困難,將消費大量資源和時間,所以筆者采用通用徑向基函數作為SVR模型的核函數,C=10,寬度系數σ=0.1。 在試驗中,分別對12維數據進行訓練,得到相應的預測模型,再對測試樣本進行預測。圖2為以磨煤機油箱油溫的訓練結果。從圖2中可以看出:磨煤機油箱油溫的預測值和真實值之間的誤差較小,各維參數訓練后的最大均方根誤差為8.76。圖3為測試數據中磨煤機油箱油溫的預測結果。 圖2 訓練樣本中真實值、預測值及誤差 圖3 測試數據中真實值、預測值及誤差 由圖3可見:預測值與真實值基本吻合,預測效果較好,測試集所有維度的最大均方根誤差為0.8。預測結果表明提出的基于SVR數據預測方法可以達到預期效果。采用這種SVR預測方法,將磨煤機運行的歷史數據作為樣本進行訓練,獲得訓練模型,再將從分布式控制系統(DCS)采集的特征參數輸入模型進行實時的預測,通過預測值與真實值之間的比對,可為電站磨煤機故障實時監測與預測提供一種重要的手段。 為了評估模型的逼近能力,采用均方根誤差XRMSE進行評價,其計算公式如下: (10) 式中:yt*為yt的逼近值。 為了評價模型的預測效果,采用均方根相對誤差XRMSRE進行評價,其計算公式如下: (11) 訓練集的最大均方根誤差為8.76,測試集的最大均方根誤差為0.8(見表2),均滿足預測要求。 表2 各指標訓練和測試結果均方根誤差 為了滿足大型機組的安全經濟運行,筆者提出一種基于相空間重構和SVR的在線估計和監測方法。通過現場設備實時采集的數據,采用SVR實現對設備的實時動態建模,能夠實時對參數進行預測,發現異常實現故障早期預警。通過某電廠320 MW機組的數據仿真,驗證了該磨煤機狀態監測方法的準確性和有效性。基于相空間重構和SVR的磨煤機故障診斷模型,為電站磨煤機故障實時診斷與預測提供了一種重要的手段,具有快速和適應范圍廣等優點。 參考文獻: [1] 楊雁梅. 電站磨煤機狀態監測與故障診斷的研究[D]. 北京: 北京交通大學, 2007. [2] 陳斌源, 朱軍. 基于徑向基函數神經網絡的中速磨煤機故障診斷[J]. 發電設備, 2011, 25(5): 323-326. [3] 紀舜堯. 主元分析在電廠故障診斷中的應用[D]. 北京: 華北電力大學, 2014. [4] 劉定平, 葉向榮, 陳斌源, 等. 基于核主元分析和最小二乘支持向量機的中速磨煤機故障診斷[J]. 動力工程, 2009, 29(2): 155-158. [5] 韓平, 王天堃, 孟永毅. 基于LS-SVM的一次風機振動在線監測及故障預警研究[J]. 機電工程, 2016, 33(5): 629-632. [6] 韓中合, 焦宏超, 徐搏超, 等. 基于EEMD樣本熵和SVM的振動故障診斷研究[J]. 汽輪機技術, 2015, 57(6): 457-460. [7] LIN H T, LIN C J. A study on sigmoid kernels for SVM and the training of non-PSD Kernels by SMO-type Methods[J]. Submitted to Neural Computation, 2003,27(1):15-23.2 預測參數選取及評估方法
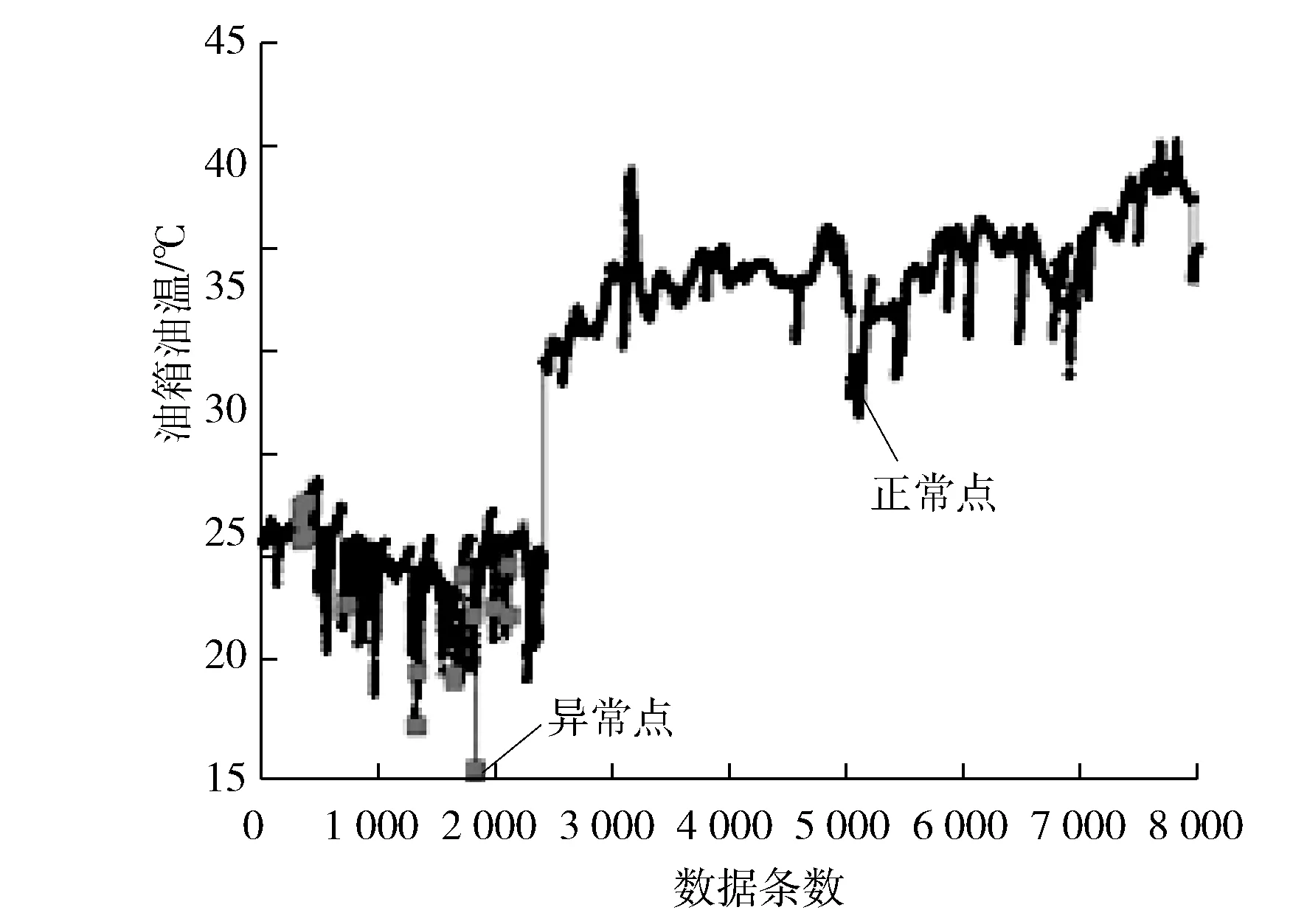

3 仿真試驗及結果
3.1 設備數據多變量時間序列的相空間重構

3.2 SVR訓練及預測
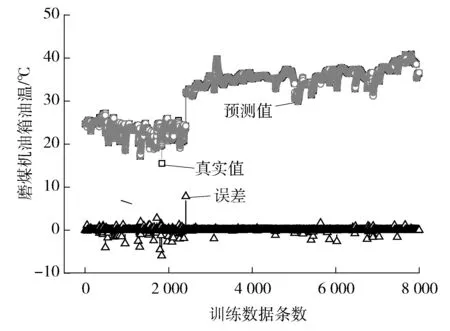

3.3 模型評價


4 結語

