基于再生運動鏈法的內螺紋加工裝置機構創新設計研究

王　強，果　霖，王　源，費琦琪，趙　聰，張天會

(云南農業大學機電工程學院，云南 昆明　650201)

機構的創新設計通常依靠設計者的知識閱歷與靈感，這往往導致創新的效率不高[1-4]。為了提高機構創新設計的效率，就需要溯本求源地對機構創新設計的內在規律進行研究，使創新設計有據可循[5]。顏鴻森教授提出的基于運動鏈再生的機構創新設計理論，被稱為再生運動鏈法，這是一種快捷、高效的設計方法，它不會因設計的多解性而遺漏方案，可以減少機構創新設計的盲目性[6]。筆者將再生運動鏈法運用到一種內螺紋加工裝置上，使其獲得與現有機構不同的新運動鏈，再對運動鏈的拓撲特性進行分析篩選，以期創造出滿足相同功能要求的同性異形機構，達到機構創新設計的目的。

1　再生運動鏈機構創新設計的原理與步驟

在機構創新設計階段，欲設計出滿足預期要求的新機構，往往會遇到一些阻礙，如設計出的機構是已有機構。而再生運動鏈法正是解決此類問題的有效方法，它的本質就是從現有機構出發，利用圖論中桿組組成原理[1,4,7]，依據原始機構的拓撲特性，將原始機構抽象為一般運動鏈，并對一般運動鏈進行數綜合，得出可能符合要求的運動鏈圖譜，再根據實際功能要求，提出設計要求與約束條件，篩選出符合要求的可行運動鏈圖譜，然后將可行運動鏈圖譜具體化為可行機構簡圖，最后刪除現有機構，得到新型機構。再生運動鏈法的一般過程如圖1所示。

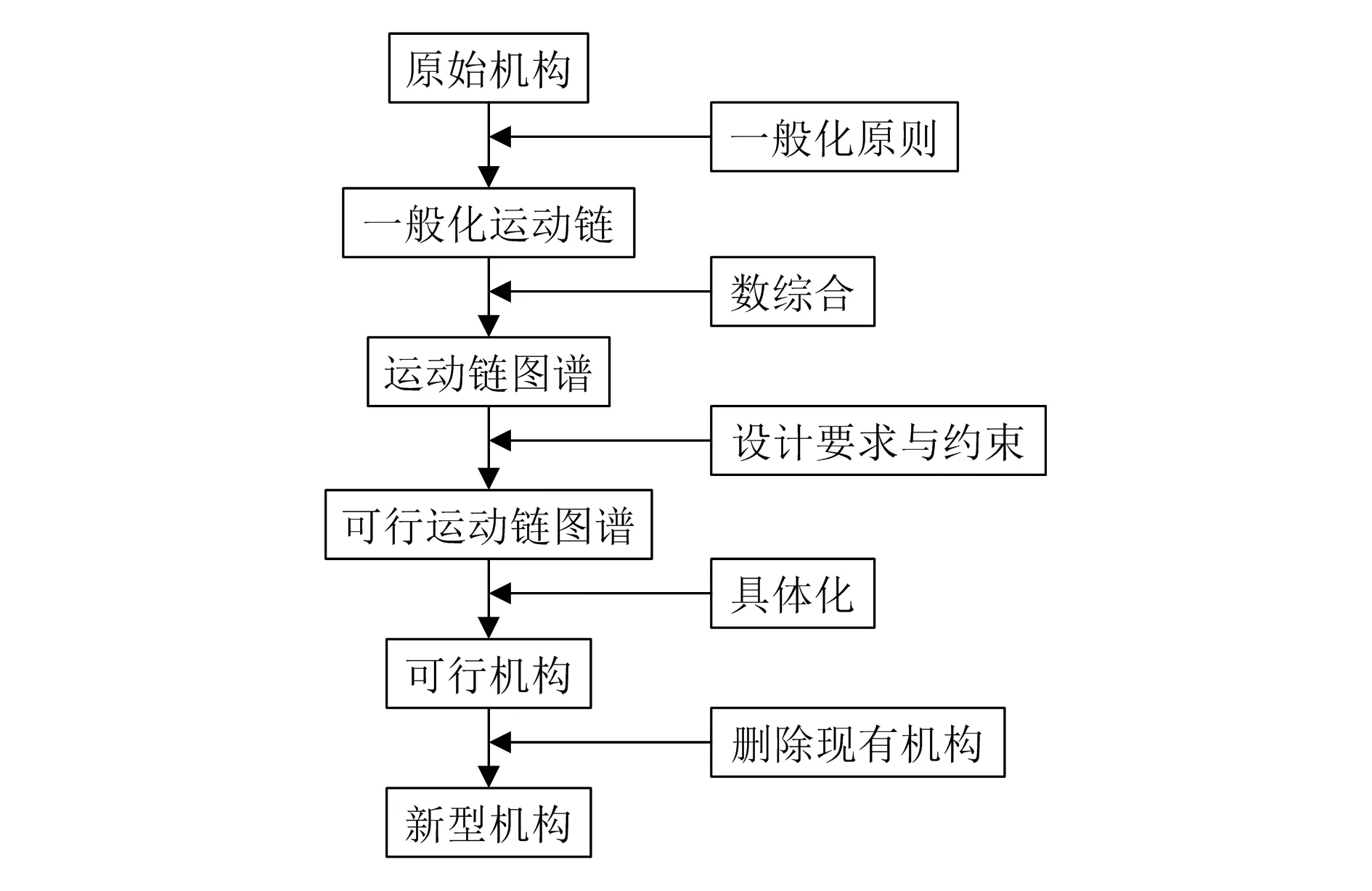
圖1　再生運動鏈法的一般過程

2　再生運動鏈法內螺紋加工裝置的機構創新設計過程

2.1　原始機構

該內螺紋加工裝置主要由曲柄滑塊機構、滾珠絲桿機構和齒輪嚙合機構組合而成，如圖2所示。曲柄滑塊機構(1～4)帶動絲桿(5)轉動,絲桿通過齒輪嚙合(h)將運動傳遞給絲錐(8),由于絲錐與固定于機架上的螺母(9)存在螺旋副，當絲錐轉動時，也會向下平動，從而同時實現絲錐的轉動與進給。

2.2　一般化運動鏈

根據一般化原則[1],通過如下步驟將該內螺紋加工裝置進行一般化處理,其對應的一般化機構圖如圖3所示。由于在一般化原則中，齒輪副與螺旋副都將用二副桿表示[8]，故需注意圖3的數字編號與圖2的數字編號并不是完全一一對應。以下步驟中的編號為圖2中的編號。

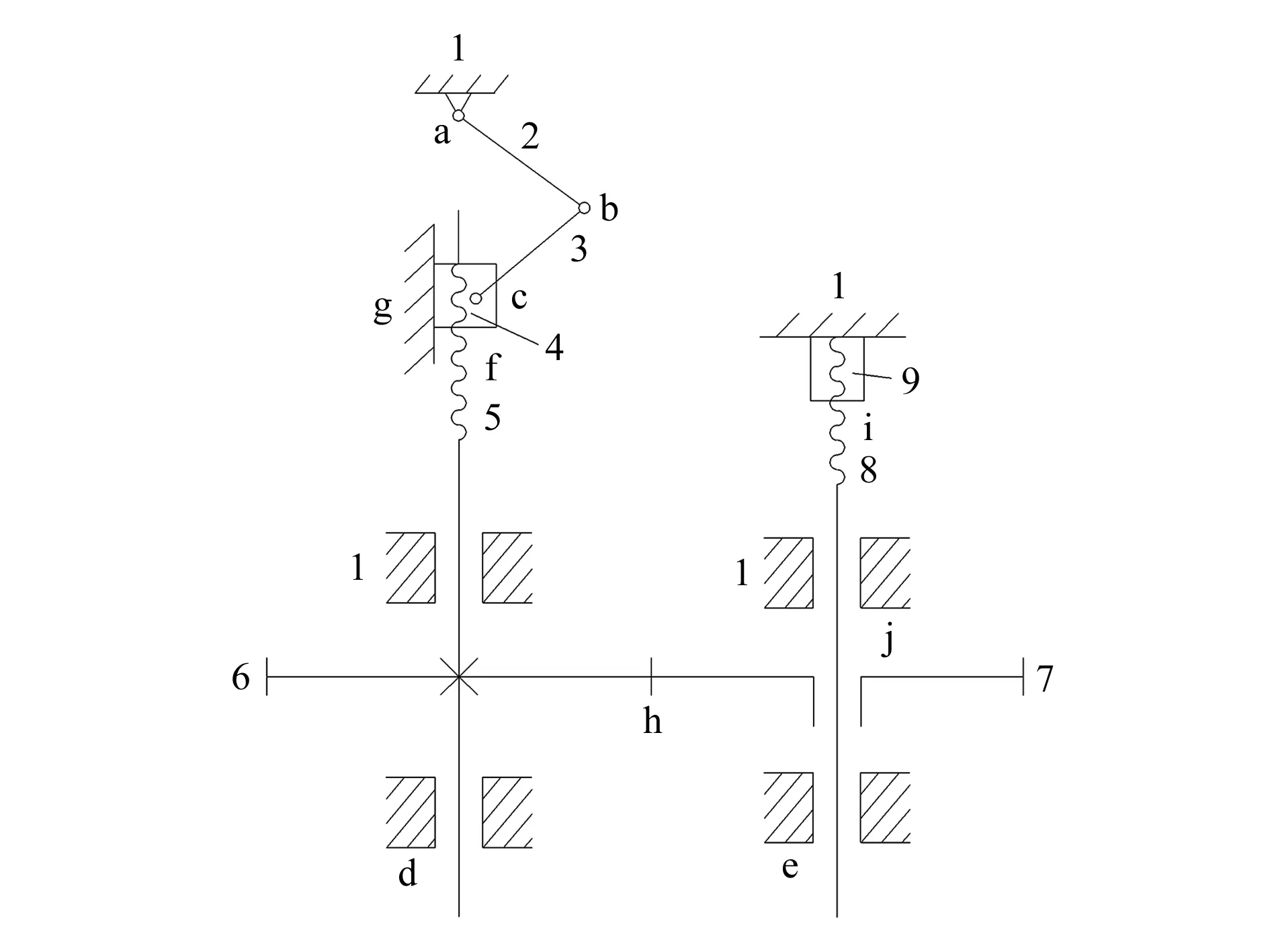
1—機架；2—曲柄；3—連桿；4—滑塊；5—絲桿；6—大齒輪；7—小齒輪；8—絲錐；9—螺母

步驟1，將機架(構件1)釋放,并一般化為五副桿；

步驟2，齒輪6，7分別一般化為2個三副桿；

步驟3，齒輪副h一般化為兩端各有1個一般化轉動副的二副桿；

步驟4，螺旋副f，i分別一般化為兩端各有1個一般化轉動副的二副桿；

步驟5，滑塊4同時存在滑動副、轉動副與螺旋副，故一般化為1個三副桿。

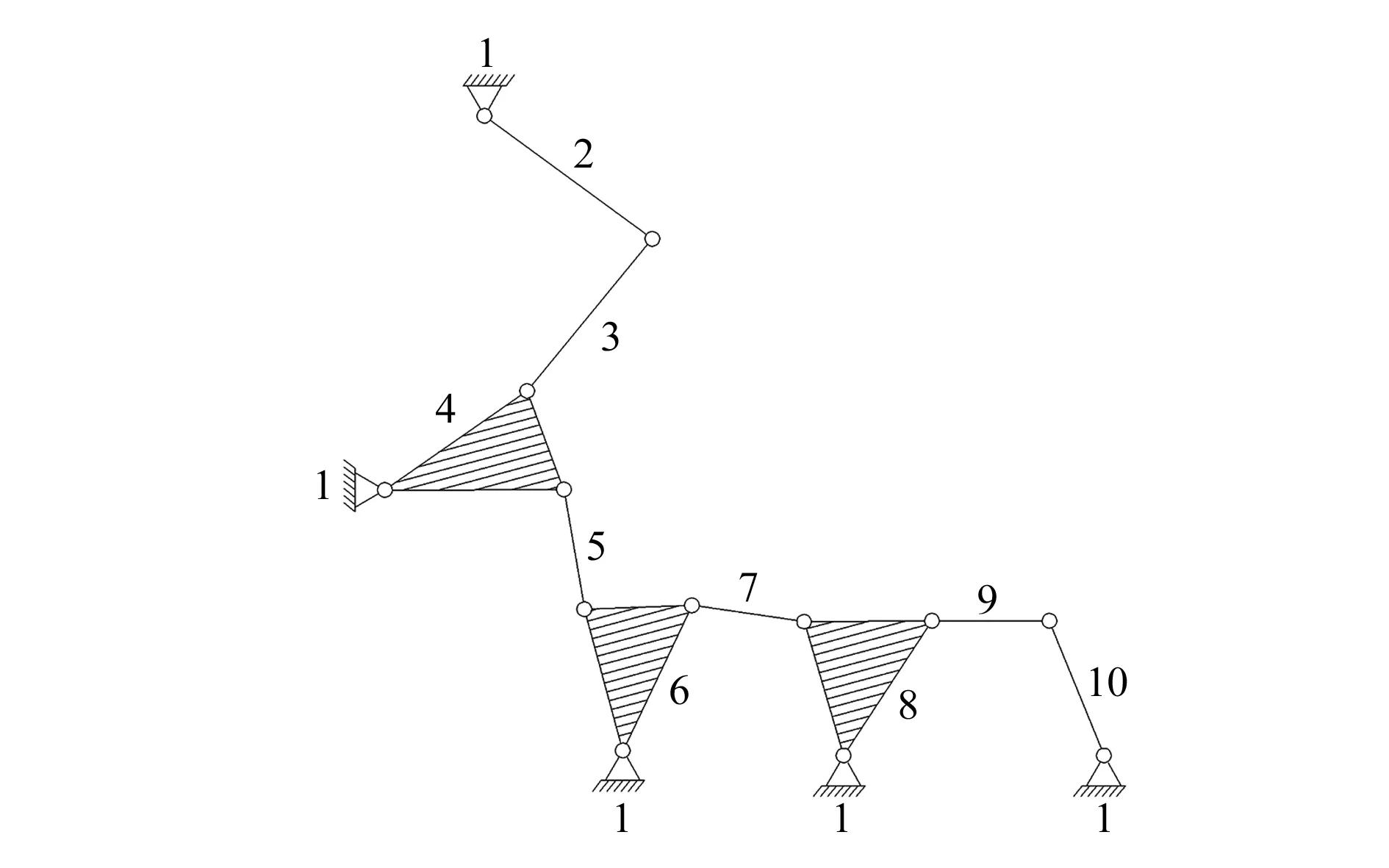
1—機架；2—曲柄；3—連桿；4—滑塊；5—螺旋副一般化后的二副桿；6—大齒輪；7—齒輪副一般化后的二副桿；8—小齒輪；9—螺旋副一般化后的二副桿；10-滑動副一般化后的二副桿

圖3內螺紋加工裝置一般化結構

在圖3中，桿4為滑塊一般化后的三副桿；桿5與桿10為螺旋副一般化后的二副桿；桿7為齒輪副一般化后的二副桿；桿6與桿8為兩個齒輪一般化后的三副桿；桿9為絲錐一般化后的二副桿。所以該裝置是個具有10個一般化連桿和13個一般化轉動副的一般化運動鏈，如圖4所示。

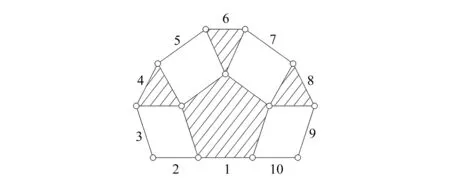
圖4　一般化運動鏈

2.3　數綜合

運動鏈圖譜中，十桿13副無復合鉸鏈的運動鏈，共有230種。其中：

1) 含有2個五副桿、8個二副桿的十桿運動鏈有2種；

2) 含有1個五副桿、1個四副桿、1個三副桿和7個二副桿的十桿運動鏈有8種；

3) 含有1個五副桿、3個三副桿、6個二副桿的十桿運動鏈有15種；

4) 含有3個四副桿、7個二副桿的十桿運動鏈有3種；

5) 含有2個四副桿、2個三副桿、6個二副桿的十桿運動鏈有57種；

6) 含有1個四副桿、4個三副桿、5個二副桿的十桿運動鏈有95種；

7) 含有6個三副桿、4個二副桿的十桿運動鏈有50種。

2.4　定義設計要求與約束

1) 必須有一個桿件作為機架,且為五副桿；

2) 必須有一個曲柄滑塊機構，即必須有2個二副桿串聯而成的桿組一端與機架相連，另一端與1個多副桿相連；

3) 曲柄兩端不允許有復合鉸鏈；

4) 必須有一個絲錐，且與機架相連。

2.5　可行運動鏈圖譜

按照設計要求與約束,可從十桿運動鏈圖譜篩選出11種運動鏈，如圖5所示。通過比較發現，圖5(b)就是現有內螺紋加工裝置的一般化運動鏈,故應刪去，因此實際上共得到10種新的可行運動鏈。

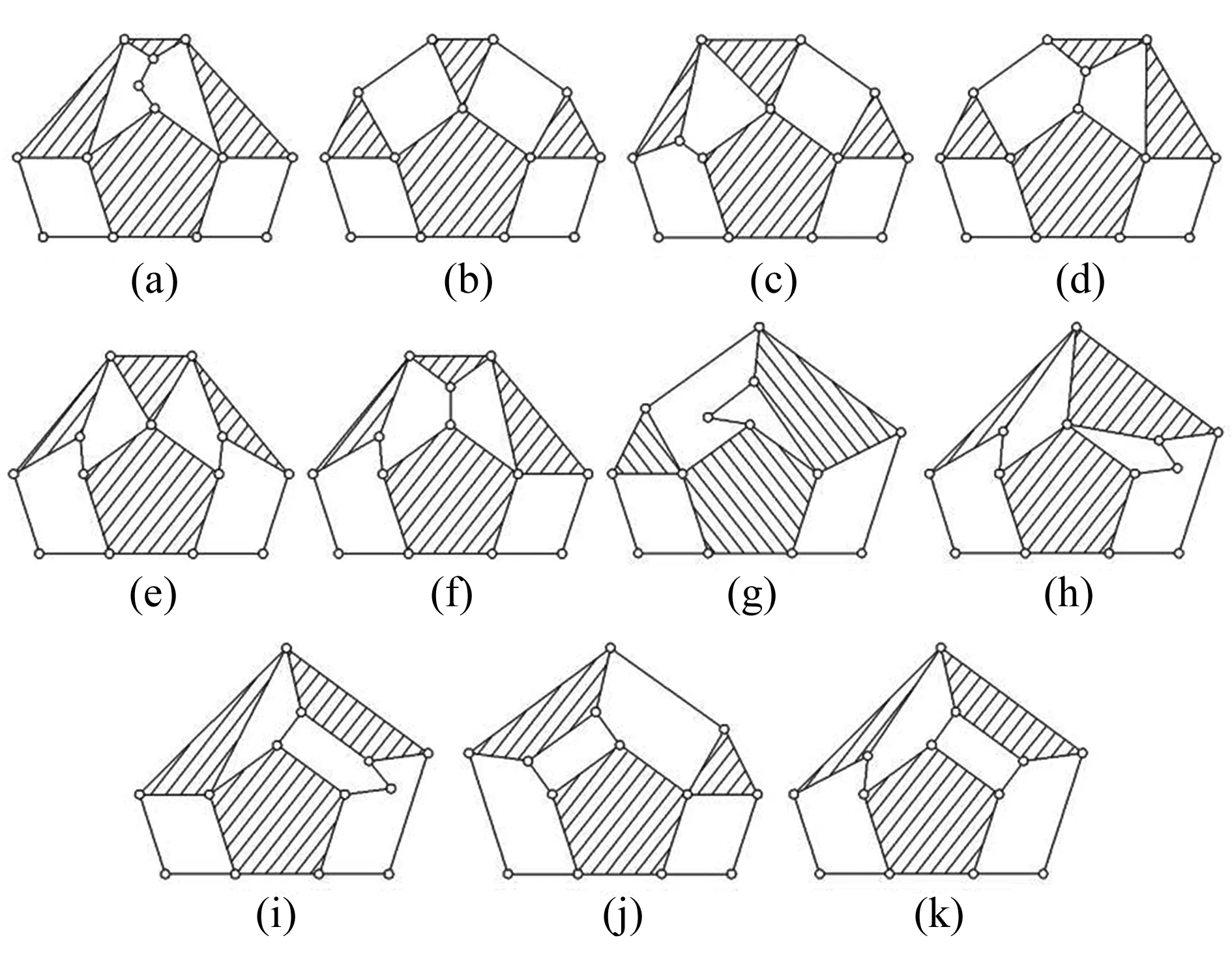
圖5　可行運動鏈

2.6　運動鏈的具體化

根據篩選出的可行新運動鏈，經過一般化原則的逆程序，將它們還原為10種不同的新機構，且完全不同于現有機構。

至此，再生運動鏈法的所有步驟都已完成，然而實際上在篩選出多種可行新運動鏈后，還要面臨選擇哪種可行運動鏈作為最終方案的問題。須知運動鏈往往是不反映構件的實際尺寸與運動副的實際空間位置關系的，而運動鏈的拓撲特性分析可以在不涉及構件實際尺寸與運動副實際空間位置關系的情況下，僅通過構件與運動副數目以及它們之間的連接關系，研究運動鏈的固有屬性[9]，為預測機構的實際特性以及選擇運動鏈作為最后方案，提供數學意義上的參考依據。

3　運動鏈的拓撲特性分析

本文隨機選取可行運動鏈中一個運動鏈與原始機構的運動鏈，對二者的機械利益、緊湊性與剛性等基本特性進行深入分析比較[10-12]。如圖6所示，圖6(a)為一個可行運動鏈，圖6(b)為原始機構的運動鏈。

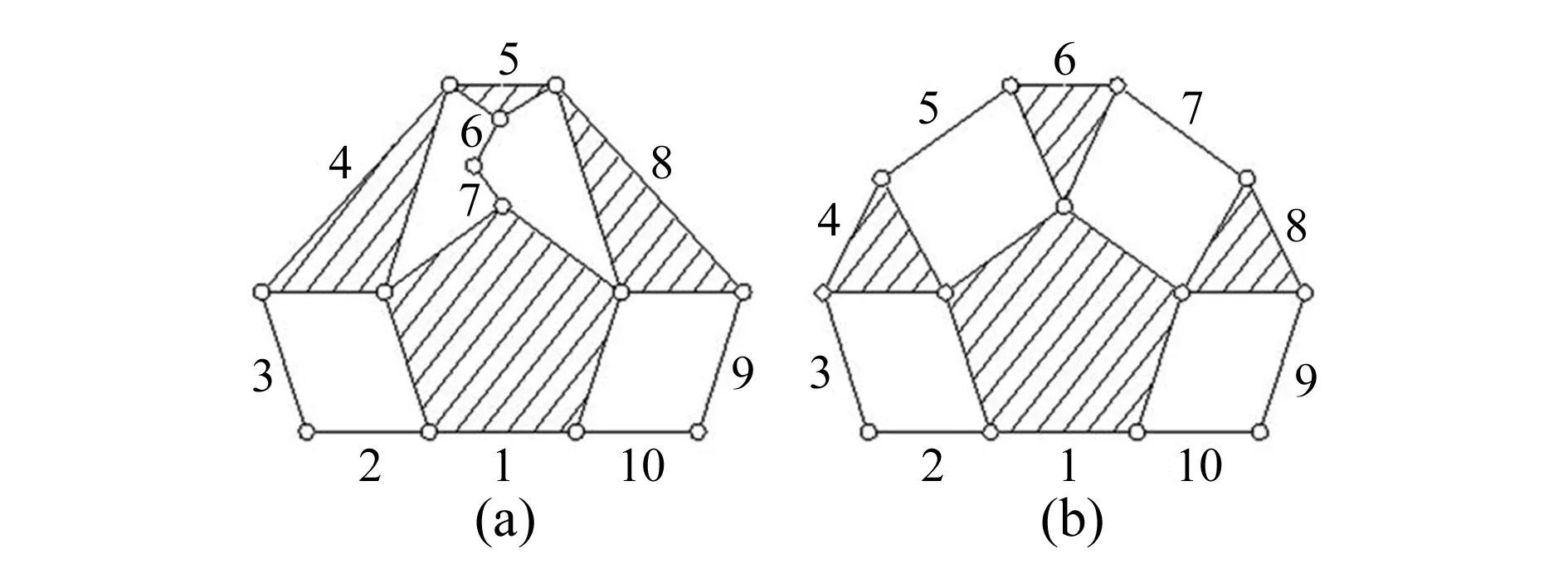
圖6　一個可行運動鏈與原始運動鏈

3.1　機械利益

機械利益是指機械系統的輸入力與輸出力之比，用于反映其運動鏈傳力性能的強弱。一個忽略能量損失的理想機械系統，即輸入功與其輸出功相等，則有：

FiΔx=FoΔy

(1)

式中：Fi，Δx分別為機械系統的輸入力與輸入力位移；Fo，Δy分別為機械系統的輸出力與輸出力位移。故可得機械利益M：

M=Fo/Fi=Δx/Δy

(2)

由式(2)可知，欲提高機械利益M，可通過選取位移較大的桿件作為輸入桿，選取位移較小的桿件作為輸出桿。適用于運動鏈的輸入與輸出為非線性關系，且運動鏈產生的非線性運動潛力越大，其機械利益可能也越大。

通常，連桿機構的輸入與輸出關系往往是非線性的，其運動鏈的拓撲結構對非線性運動潛力有著不小的影響。由文獻可知，在運動鏈的一個閉環中，所包含的桿件數越多，其非線性運動潛力越大，即其獲得的機械利益也越大。

如圖6(b)所示，其運動鏈含有4個閉環，即1—2—3—4，1—4—5—6，1—6—7—8，1—8—9—10，都為四桿閉環。而圖6(a)中的運動鏈含有4個閉環，其中有2個四桿閉環：(1—2—3—4，1—8—9—10)和2個五桿閉環：(1—4—5—6—7，1—8—5—6—7)。由于五桿閉環的非線性運動潛力大于四桿閉環的非線性運動潛力，所以圖6(a)所示的運動鏈比圖6(b)所示的運動鏈可能獲得更大的機械利益。

3.2　緊湊性

結構緊湊的機構具有良好的靜態特性，且占用的空間較小。在不考慮桿件長度的情況下，桿件數及運動副數越少，運動鏈就越緊湊。在具有相等桿件數及運動副數的運動鏈中，可以通過定義桿件間的距離關系，以此定量比較它們的緊湊性。

將兩桿間的距離關系定義為：在運動鏈中，從一桿出發到達另一桿所經過的最少運動副數。根據定義，可以得到運動鏈的距離矩陣D。在矩陣D中，元素dij為從桿i出發到達桿j所經過的最少運動副數，其中dij=0。在矩陣D中∑dij稱為運動鏈的距離值。距離值越小的運動鏈，結構就越緊湊。

根據定義，可分別寫出圖6(a)運動鏈與圖6(b)運動鏈的距離矩陣D1,D2。

分別將這兩個矩陣中各自的所有元素求和，可得圖6(a)運動鏈的距離值為186，圖6(b)運動鏈的距離值為208。因為圖6(a)運動鏈的距離值較圖6(b)運動鏈的小，所以圖6(a)運動鏈的緊湊性要好于圖6(b)運動鏈。

3.3　剛性

在實際機械結構中，桿件的剛性由它的尺寸、彈性系數以及實際支承情況決定。而本文中，不考慮桿件的尺寸，僅將其視為彈性體，每個桿的支點數目等于該桿的運動副數，即該桿的連通度。故可得剛度矩陣K=[kij]，其中:

(3)

式中：Ci,Cs,Cj分別為桿i,s,j的連通度。

式(3)中，當i≠j時，在該分式的分母中，桿s代表從桿i出發到達桿j的最短路徑所經過的所有桿件。若兩桿間存在不止一條最短路徑，則取使kij最小的路徑為最短路徑。在運動鏈的剛度矩陣K中，每一行元素之和，表示該行所對應的桿的剛度，矩陣全部元素之和則對應該運動鏈的剛度。

根據定義，可分別寫出圖6(a)與圖6(b)運動鏈的剛度矩陣K1,K2：

根據定義，可以得出圖6(a)運動鏈的剛度∑kij=174.65，同理得出圖6(b)運動鏈的剛度為173.06，故圖6(a)運動鏈的剛度要大于圖6(b)運動鏈的剛度。

本節只隨機選取了一種運動鏈與原始機構的運動鏈進行對比分析，而在余下的運動鏈中，可能會存在比所選的運動鏈具有更優拓撲特性的運動鏈或者比原始機構運動鏈更差拓撲特性的運動鏈，因此實際篩選時需要同時比較所有可行運動鏈的拓撲特性，才能科學地得出合適的運動鏈。

4　結束語

再生運動鏈法是一套系統化、程式化并含有理論支撐的設計方法，既不會因設計的多解性而遺漏方案，也不會因其多解性而重復方案，可有效提高創新設計效率，減少創新設計盲目性，幫助設計人員找到符合要求的新運動鏈。結合運動鏈的拓撲分析，研究運動鏈的固有屬性，設計人員可以從數學層面上直觀、定量地了解運動鏈的特性，并易于比較運動鏈之間的特性差異，使設計方案保有預見性與合理性，可為設計人員提供充分的理論參考依據。

參考文獻：

[1]顏鴻森.機械裝置的創造性設計[M].姚燕安，譯.北京：機械工業出版社，2002.

[2]鄒慧君.機構系統設計[M].上海：上海科學技術出版社，1996.

[3]黃純穎.機械創新設計[M].北京：高等教育出版社，2000.

[4]張春林.機械創新設計[M].北京：機械工業出版社，1999.

[5]張寧，姚立綱，張煒.基于再生運動鏈法的游梁式抽油機機構創新[J].機械設計與研究, 2014(5):41-44，49.

[6]葛茂忠.基于運動鏈再生創新設計理論的沖擊攻絲機的研制[J].新技術新工藝,2010(2)：48-50.

[7]盧開澄.圖論及其應用[M].北京：清華大學出版社，1984.

[8]葛茂忠.機構創新設計理論及其在沖擊攻絲機上的應用研究[D].昆明：昆明理工大學，2004.

[9]彭朝琴，符煒，郭承志. 概念設計中常用基本鏈型的拓撲特性分析與比較[J].機械設計,2002(8):48-51.

[10] RAO A C.Topological characteristics of linkage mechanism with particular reference to platform-type robots[J]. Mechanism & Machine Theory,1995,30(1):33-42.

[11] RAO A C.Structure-based dynamic characteristics of planar linkages including platform-type robots[J].Journal of Robotic Systems,1997,14(8):621-629.

[12] RAO A C.On the performance of kinematic chains[J]. Transactions of the Canadian Society for Mechanical Engineering,1988,12(2):99-102.