復雜TTI介質穩定的純qP波波場模擬方法

胡書華　王宇超　劉文卿　周　陽

(①中國石油勘探開發研究院西北分院，甘肅蘭州 730020；②同濟大學海洋與地球科學學院波現象與反演成像研究組，上海 210092)

1　引言

隨著勘探目標的復雜化與多樣化，地震勘探對地下介質精確成像的需求不斷提高。Baysal等[1]于1983年提出的逆時偏移(Reverse time migration，RTM)技術，因其成像精度高、適應復雜介質等優點，已得到廣泛的研究與應用[2-5]； 而作為縱波勘探中逆時偏移技術的基礎，高效而精確的準縱波(quasi-P wave，qP波)模擬算法也處于持續發展中。同時，由于地下介質普遍具有各向異性特性，因此當前精確成像算法對地下各向異性高精度近似的要求越來越高[6]。

自1998年Alkhalifah[7]提出將各向異性物性對稱軸方向橫波速度設置為零的聲學近似思想以來，基于該思想的各向異性介質qP波模擬算法得到快速發展： Alkhalifah[8]導出聲學近似下TI介質四階控制方程， Zhou等[9]將該方程分解為兩個二階微分方程； Du等[10]和Fowler等[11]也導出了不同形式的二階qP波控制方程。

近年，Fletcher等[12]、Duveneck等[13]、Zhang等[14]發現這些方程在實際應用中會遇到“聲學近似導致的橫波干擾”和“物性對稱軸變化劇烈處波場傳播不穩定”兩個問題，分析其原因并提出了不同的解決方案： Flecher等[12]采用添加有限橫波速度的方法，導出有限橫波方程，消除偽橫波并保證穩定性； Duveneck等[13]則從一般介質本構方程出發，導出了更加符合物理意義的穩定的qP波傳播控制方程； Zhang等[14]在該方程中添加自共軛二階微分算子來保證其穩定性。

近期關于純qP波模擬的研究主要集中在有效各向同性模型近似算法和擬微分算子分解方法。如Alkhalifah等[15]的各向同性近似算法在很大程度上改善了RTM效率； Xu等[16，17]提出擬微分算子分解方法并對其進行了改進，將偽微分算子分解為一個標量算子和一個微分算子，該方法得到的波場不受偽橫波干擾，且波場模擬精度較高。

本文基于Xu等[17]的擬微分算子分解思想，分析了分解后標量算子和橢圓微分算子的頻散特性，推導出對應的TTI介質一階qP波控制方程，并用交錯網格高階有限差分算法對方程實施求解，得到復雜TTI介質穩定的純qP波模擬的結果。

2　新的純qP波控制方程

2.1　算子分解思路

從一般介質本構關系出發，求解Christoffel方程得到qP-qSV耦合相速度公式，進而可導出各向異性介質頻散關系。據Alkhalifah[7]聲學近似思想，令VSz=0，有VTI介質qP-qSV耦合頻散關系

(1)

式中：ω為角頻率；VPz為P波垂向速度；ε和δ為Thomsen各向異性參數；kx、ky和kz分別為x、y和z方向的波數。

考慮Alkhalifah[8]給出的VTI介質標量擬微分方程

(2)

該式即為VTI介質qP波傳播控制方程，注意方程中的所有參數都是空間變化的。式(2)的頻散關系與式(1)相同，即與彈性P波的頻散關系一致，表明其能夠準確地模擬qP波傳播。然而，式(2)是一個偽微分方程，在數值上不易求解。因此，Xu等[17]提出將式中偽微分算子分解為一個橢圓微分算子和一個標量算子的思路。式(2)對應的頻散關系可容易地表達成

(3)

定義單位波數矢量

(4)

將其代入式(3)，同時對式(3)中根式項進行變換，得到

(5)

記式(5)等號右側含有單位波數矢量分量的乘積項為標量算子Se，剩余部分變換到時空域，則為橢圓微分算子

(6)

(7)

式(6)即為橢圓微分算子； 式(7)為標量算子。

式(3)～式(7)即為算子分解下的橢圓微分算子分解方法。算子分解的主要目的在于改造原偽微分方程，將其中不易求解的偽微分算子分解為容易求解的橢圓微分算子和標量算子，在保持波場模擬精度的同時實現方程高效求解。

2.2　算子頻散特性分析

考慮對新算子的頻散特性進行分析，同時與精確qP波頻散關系進行對比，以研究新算子對于波場的作用。

式(6)對應的頻散關系可寫成

(8)

考慮二維情況，給定參數VPz=3000m/s、ε=0.24、δ=0.1，繪制精確頻散關系曲線(式(1))、橢圓微分算子頻散關系曲線(式(8))及本文推導的式(6)和式(7)對應的頻散關系曲線。由圖1可見，橢圓微分算子接近于精確qP波頻散關系，然而兩者存在明顯的數值差； 分析式(8)可知兩者相差的量來自于標量算子Se的作用。同時，采用本文新方程所得頻散關系曲線與精確頻散關系曲線相一致。因此可知，該偽微分算子分解方法實際上相當于用標量算子Se對橢圓微分算子進行校正。

進一步分析校正項Se的作用，記標量算子Se=1+ΔSe，則有

(9)

二維情況下，將頻散關系式轉換到極坐標系(R，θ)下，繪制的精確頻散關系曲線、橢圓微分算子關系曲線、標量算子ΔSe項頻散曲線以及本文新算子的頻散關系曲線如圖2所示。可見ΔSe項的數值在-0.05～0之間，是對橢圓微分算子的一種微小補償，目的在于將其校正到精確頻散關系。同時從該圖可知，式(6)與式(7)組成的新算子可保持精確的qP波頻散關系， 因此具有較高的qP波模擬精度。

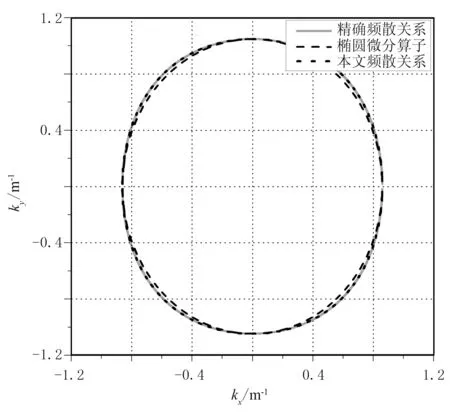
圖1　　　　精確的qP波頻散關系、橢圓微分算子及本文頻散關系對比

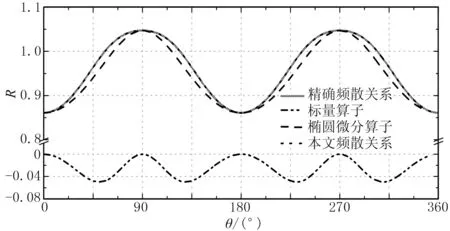
圖2　　　　極坐標下精確頻散關系、標量算子、橢圓微分算子及本文頻散關系對比

2.3　TTI介質純qP波控制方程

為了數值實施方便，引入輔助波場p、q和r，同時將式(6)寫為一階形式

(10)

Se=

(11)

式(11)與式(10)共同組成了VTI介質純qP波控制方程。

對于TTI介質，仿照Zhang等[14]和Bube等[18]的確保穩定性做法，在旋轉坐標系下引入自共軛微分算子

(12)

式中： “·”為u、p、q、r中任一種量；θ表示TTI介質物性對稱軸傾角；φ為對稱軸方位角； 上標“T”表示轉置運算。用新的算子依次替換式(10)和式(11)中的微分算子，可得旋轉坐標系下的TTI介質純qP波傳播控制方程

(13)

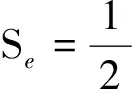
(14)

式(12)～式(14)共同構成TTI介質純qP波傳播控制方程。該控制方程來自于偽微分算子分解得到的新算子，與精確的qP波頻散關系相同，且方程推導過程中未做任何近似，將此用于TTI介質qP波模擬具有較高的精度。

3　數值算法

本文采用交錯網格高階有限差分數值解法求解式(12)～式(14)，在t時刻計算質點位移u，在t-Δt/2時刻計算輔助波場p、q和r。

考察式(12)～式(14)發現，t+Δt時刻波場u的計算不僅需要t時刻的波場u，還需t+Δt/2時刻輔助波場p、q和r分別關于x、y和z的微分； 同樣地，t+Δt/2時刻輔助波場p、q和r的計算不僅需t-Δt/2時刻的波場p、q和r，還需t時刻波場u關于x、y和z的微分。因此，為了避免插值，提高計算精度，本文采用Lebedev交錯網格[19，20](圖3)。其中：在方點位置處計算波場u和標量算子Se； 在圓點位置處計算輔助波場p、q和r。

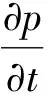
(15)

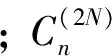
(16)

式中：f(t)為震源函數；F為f的離散變量。

圖3　式(12)～式(14)的Lebedev交錯差分網格格式

這里需要注意的是，式(13)和式(14)中雖然都有Gxu、Gyu和Gzu項，但前者在p、q和r的位置計算，而后者在u的位置計算。兩者計算的位置不同，雖然可以通過插值得到不同位置的數值，但為了保證計算的精度，對兩處位置分別計算波場u的梯度。兩者差分公式略有區別，可根據網格位置類似寫出。計算復雜度雖然增加了波場u梯度的1次計算，但保證了波場模擬的精度。

至此，給出了用Lebedev交錯網格高階有限差分求解式(12)～式(14)的數值算法。為了保證波場模擬的精度和穩定性，引入了Lebedev交錯網格，同時采用波場梯度2次計算的數值算法策略。

4　模型數據測試

4.1　均勻TTI介質模型

給定均勻TTI介質參數：VPz=3000m/s，ε=0.1，δ=0.024，網格數為400×400，網格尺寸10m×10m，震源子波主頻為16Hz，震源位于網格中心位置，時間步長1ms，時間方向采用2階差分，空間方向采用10階差分。其0.6s的波場快照如圖4所示。可見Fletcher有限橫波法和本文方法得到的波場中qP波成分與彈性波場中P波成分一致，表明兩者均能較好地保持P波傳播特征。但是有限橫波法得到的qP波場中存在明顯的殘余橫波干擾，而本文方法得到的純qP波場已經完全消除了殘余橫波干擾，表明本文方法不受偽橫波干擾的影響。

4.2　雙層TTI介質模型

設計雙層TTI介質模型如圖5所示，模型在2500m深度位置存在反射界面。對其分別進行常規網格有限差分彈性波模擬、有限橫波法模擬以及本文提出的純qP波方法模擬，所得結果如圖6所示。模擬參數與上述均勻TTI介質一致。

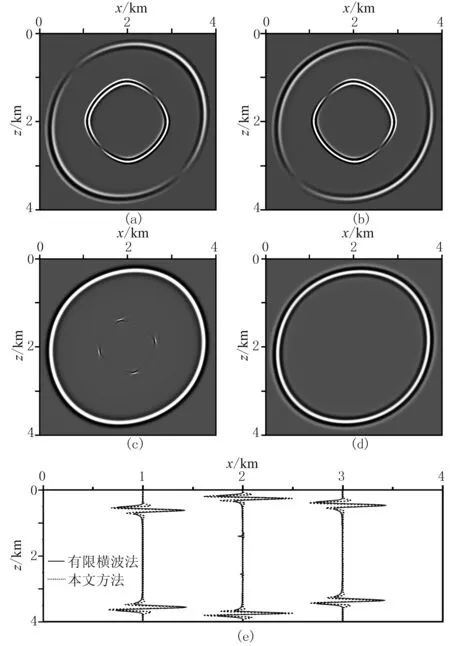
圖4　均勻TTI介質模型600ms波場快照對比

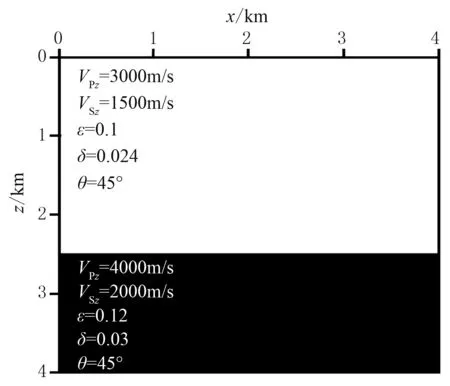
圖5　水平雙層TTI介質模型

圖6　水平雙層TTI介質模型550ms波場快照對比

分析圖6可知，從全彈性波波場快照可以分辨出直達縱波、直達橫波以及各種轉換波，如反射縱波、反射橫波、透射縱波、透射橫波；而有限橫波法得到的波場中不僅存在殘余直達橫波干擾，也存在殘余的透射和反射橫波干擾；本文方法得到的純qP波波場中只有縱波成分，不存在殘余橫波干擾，且縱波波前特征與全彈性波場中的縱波特征一致，證明本文方法的有效性。

4.3　復雜TTI介質模型

本文從BP-TTI模型中截取一塊各向異性參數復雜的區域，如圖7所示。模型網格數為1801×1801，網格尺寸為6.25m×6.25m。可看到模型中存在大量陡傾斷層，各向異性對稱軸傾角參數θ在某些位置有突變現象，這對于波場的穩定模擬帶來挑戰。

將震源放置于模型中心位置處，采用常規網格有限差分彈性波模擬方法、有限橫波方法、本文方法分別進行波場模擬，得到1000ms和1500ms波場快照如圖8和圖9所示。

圖9　BP TTI模型1500ms波場快照對比

由波場模擬結果可知，有限橫波法和本文方法所得到的波場，其P波波前特征與全彈性波波場一致，表明兩者對于波場中的縱波成分能較好地進行模擬。但是，有限橫波法波場中存在殘余偽橫波干擾，且殘余偽橫波在傳播過程中又產生殘余的反射、透射橫波干擾；而本文方法能得到干凈的純P波波場，不存在殘余橫波干擾。表明本文提出的方法能夠適應各向異性物性對稱軸參數劇烈變化情況，得到穩定的無橫波干擾的純qP波波場。

5　結論

本文基于Xu的偽微分算子分解思路，結合旋轉坐標系下的自共軛微分算子導出穩定的一階純qP波控制方程，同時在Lebedev交錯網格框架下給出其高階有限差分算法，在復雜各向異性模型中得到了穩定傳播的qP波場。由算子頻散分析以及均勻TTI模型、雙層TTI模型以及復雜TTI介質模型純qP波波場模擬試驗可知，相對于其他qP波模擬算法，本文提出的純qP波模擬算法不受偽橫波的干擾，且對各向異性物性對稱軸參數變化有更好的適應性，在物性對稱軸傾角參數變化劇烈時也能得到穩定的純qP波波場。

[1]Baysal E,Kosloff D D,Sherwood J W C.Reverse time migration.Geophysics,1983,48(11)：1514-1524.

[2]劉文卿,王宇超,雍學善等.基于GPU/CPU疊前逆時偏移研究及應用.石油地球物理勘探,2012,47(5)： 712-716.

Liu Wenqing,Wang Yuchao,Yong Xueshan et al.Prestack reverse time migration on GPU/CPU co-parallel computation.OGP,2012,47(5)：712-716.

[3]劉文卿,王西文,劉洪等．鹽下構造速度建模與逆時偏移成像研究及應用．地球物理學報,2013,56(2)：612-625．

Liu Wenqing,Wang Xiwen,Liu Hong et al.Application of velocity modeling and reverse time migration to subsalt structure.Chinese Journal of Geophysics,2013,56(2)：612-625.

[4]劉定進,蔣波,李博等.起伏地表逆時偏移在復雜山前帶地震成像中的應用.石油地球物理勘探,2016,51(2)：319-324.

Liu Dingjin,Jiang Bo,Li Bo et al.Rugged-topography reverse time migration in complex piedmont zone.OGP,2016,51(2)：219-324.

[5]姜國博,曾慶芹,李虹等.逆時偏移技術在土庫曼斯坦地區的應用.石油地球物理勘探,2017,52(增刊2): 81-85,103.

Jiang Guobo,Zeng Qingqin,Li Hong et al.Application of reverse time migration in Turkmenistan area.OGP,2017,52(S2): 81-85,103.

[6]韓令賀,何兵壽.VTI介質一階準P波方程正演模擬及邊界條件.石油地球物理勘探,2010,45(6)：819-825.

Han Linghe,He Bingshou.First-order Quasi-P wave equation forward modeling and boundary conditions in VTI medium.OGP,2010,45(6)：819-825.

[7]Alkhalifah T.Acoustic approximation for processing in transversely isotropic media.Geophysics,1998,63(2)： 623-631.

[8]Alkhalifah T.An acoustic wave equation for aniso-tropic media.Geophysics,2000,65(4)：1239-1250.

[9]Zhou H,Zhang G,Bloor R.An anisotropic acoustic wave equation for modeling in 2D TTI Media.SEG Technical Program Expanded Abstracts,2006,25：194-198.

[10]Du X,Fletcher R P,Fowler P J.A new pseudo-acoustic wave equation for VTI media.70th EAGE Conference & Exhibition,Extended Abstracts,2008：H033.

[11]Fowler P J,Du X,Fletcher R P.Coupled equations for reverse time migration in transversely isotropic media.Geophysics,2010,75(1)：S11-S22.

[12]Fletcher R P,Du X,Fowler P J.Reverse time migration in tilted transversely isotropic (TTI) media.Geo-physics,2009,74(6)：WCA179-WCA187.

[13]Duveneck E,Bakker P M.Stable P-wave modeling for reverse time migration in tilted TI media.Geophy-sics,2011,76(2)：S65-S75.

[14]Zhang Y,Zhang H Z,Zhang G Q.A stable TTI re-verse time migration and its implementation.Geophysics,2011,76(3)：WA3-WA11.

[15]Alkhalifah T,Ma X,Waheed U B et al.Efficient anisotropic wavefield extrapolation using effective isotropic models.75th EAGE Conference & Exhibition,2013：Tu-01-16.

[16]Xu S,Zhou H.Accurate simulations of pure quasi-P-waves in complex anisotropic media.Geophysics,2014,79(6)：1-8.

[17]Xu S,Tang B,Mu J et al.Elliptic decomposition of quasi-P wave equation.77th EAGE Conference & Exhibition,2015：We P6 12.

[18]Bube K P,Nemeth T,Stefani J P et al.On the instability in second-order systems for acoustic VTI and TTI media.Geophysics,2012,77(5)：T171-T186.

[19]Hu S H,Wang X W,Sun J Q et al.Stable simulating algorithm of pure quasi-P wavefield in complex anisotropic media.78th EAGE Conference & Exhibition,2016：We SRS3 04.

[20]李娜,李振春,黃建平等.Lebedev網格與標準交錯網格耦合機制下的復雜各向異性正演模擬.石油地球物理勘探,2014,49(1)：126-131.

Li Na,Li Zhenchun,Huang Jianping et al.Numerical simulation with coupling Lebedev and standard staggered grid schemes for complex anisotropic media.OGP,2014,49(1)：126-131.

[21]董良國,馬在田,曹景忠等.一階彈性波方程交錯網格高階差分解法.地球物理學報,2000,43(3)：411-419.

Dong Liangguo,Ma Zaitian,Cao Jingzhong et al.A staggered-grid high-order difference method of one-order elastic wave equation.Chinese Journal of Geophysics,2000,43(3)：411-419.