基于通信時分框架的單站無源動目標定位技術

高元峰，江　漫，葛　蕾，賈鐵燕

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0　引言

現代戰爭中各種高新技術兵器對于作戰武器平臺生存的威脅日趨嚴重，除了實現更多平臺間的信息情報共享、資源協同支持，還要提升平臺自身的綜合作戰能力，形成更大的感知域、拒止域和掌控域。

長久以來，武器平臺的單站動目標定位技術都是其能力建設的重中之重，而主動探測手段由于原理簡單、性能優越等特點長期占據主導地位，但隨著各種電子對抗技術的發展，主動探測的電磁輻射風險日甚而其回報驟減，同時以被動相參定位(Passive Coherent Location，PCL)技術[1-3]為代表的單站無源定位技術開始不斷發展。無源定位技術[4-6]具有良好的電磁隱蔽特征，同時其在反隱探測、設備成本方面具有較大優勢，已經成為世界各國新技術手段發展的熱點。

本文主要針對單站無源[7-8]動目標定位技術體制和基于通信時分結構下時差變化率[9-10]進行理論分析與仿真研究，較好地解決了單站徑向探測的瓶頸限制和測量精度問題，提升了整體的定位能力。

1　　　　單站無源動目標定位體制分析及常規算法的技術限制

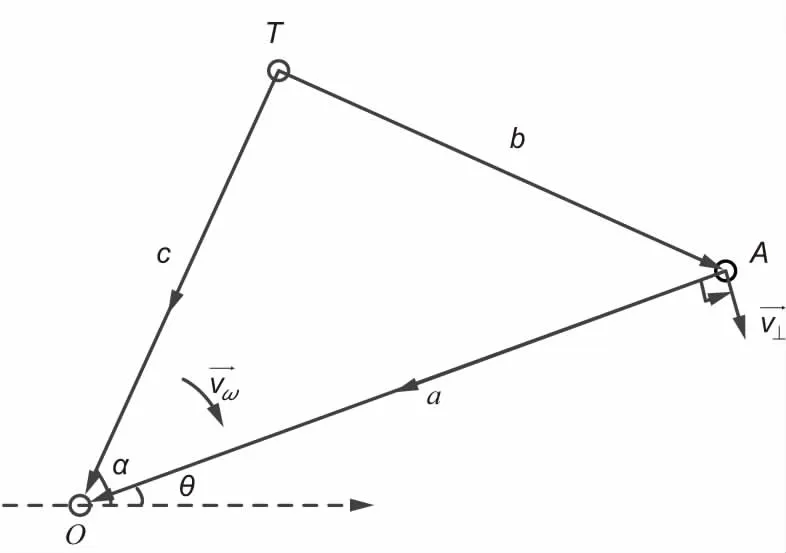
圖1　單站無源定位基本模型

在具體應用算法研究中，會根據不同設定，補充三角形已知要素使其合理并可解。比如，當把點T設定為第三方電波輻射源(如廣播電臺等)，并利用直達波和折射波間的波程差估計(其本質是已知三角形一條邊(c)、一個內角(∠TOA)和另一條邊的條件(兩邊差))可以得到目標A的位置，即PCL的基本概念模型。

考慮到所提基礎三角形模型的結構需要，有單運動平臺對固定目標的無源定位技術研究，其設定目標A固定不動而偵測站O發生運動的條件。此時由于O的合作性運動導致隨時間變化的一系列連續三角形，通過多次測角可統計交匯位置，從而得到對目標A的定位估計。

在固定單站無源定位技術的研究中，目標和偵測站間的徑向位移測量模糊是十分棘手的難題。在圖1的模型中，如果目標A運動則會得到一系列角αi，i=1，2...，i為觀測時刻。顯然有

(1)

近些年，有學者提出基于角度變化率、多普勒頻率變化率、方向信息、角速度及多普勒頻率變化率信息等技術方法實現單站無源動目標定位能力。其算法核心都是基于對多普勒頻率估計推測目標的徑向運動，同時算法對于對象的運動規律還有較多要求，不具備廣泛的適應性和動態穩健性。

基于多普勒頻率與變化率的方法，前提條件不是需要約束目標的運動規律(如勻速直線運動)，就是要求明確目標的運動速度或載波頻率信息，其假設顯然不具有良好的工程實用基礎和應用前景。其中，多普勒頻率直接反映了目標的相對運動速度和頻率之間的物理關系，如果知道目標的多普勒頻率就等于知道目標的徑向運動速度。但對于非合作方獲得目標的多普勒頻率幾乎是不可能達到的條件，因此該方法研究甚少。而多普勒頻率變化率估計規避了目標頻率已知的要求，通過連續測頻得到頻差的方式提取可用信息。而多普勒頻率變化率反映目標徑向速度的變化值，是目標運動加速度的直接物理體現，對其的研究依舊存在對運動規律的約定。如標準二維定位算法(要求目標做勻加速運動)、EKF[11-12]的定位與跟蹤濾波算法(要求目標做平滑運動)等。

2　基于時差變化率增強的新定位技術

通信系統作為眾多分散收發信息交互活動的支撐，需要具有嚴格的規則和固有的循環。現代通信系統中，時分復用[13]體制是解決多用戶接入、低概率截獲和提高資源利用率的重要方式。系統通過建立統一、標準化的時間基準框架，對通信帶寬資源進行時間片劃分，將不同用戶和各種業務按需進行時隙(時間片)資源分配，而用戶時隙以最大運行時間周期循環，即

(2)

式中，Tn為第n個時隙的結構集合；Δt為時隙的時間片寬度；T為整體時間運行周期。單個用戶因需會獲得1個以上的時隙資源分配，而在使用中用戶也有個別具體時隙未使用的情況，但總體上其通信電磁行為總是發生在總周期T的整數倍時刻。

時隙結構及其規律是通信信號一種較為顯著的特征，而在內部還有很多的同步、循環、固定的信息或結構。在對目標有一定分析和了解的基礎上，都是可能成為提取其行為周期性特征的依據。

2.1　通信的時分復用原理和體制結構

通過對于定位目標電磁行為規律的掌握和時間序列的估計，可以提供一種核心三角結構關系的新理解。它區別于傳統PCL等技術的突出特點是，通過研究目標，不單純依靠基本物理信號參數測量，掌握并利用其上層電磁行為規律信息特征建立分析模型，其估計精度優勢明顯。需要強調的是此種估計可以替代之前多普勒頻率及其變化率測量的方法，解決單站模型中徑向測量模糊的難題。

建立基于通信時分框架的時差變化率增強單站無源動目標定位技術，其核心模型由固定偵測站O和運動目標A組成，t0，t1，...，tn...分別是不同的偵測時刻，以其中的t0，t1為例建立三角結構關系，結構如圖2所示。

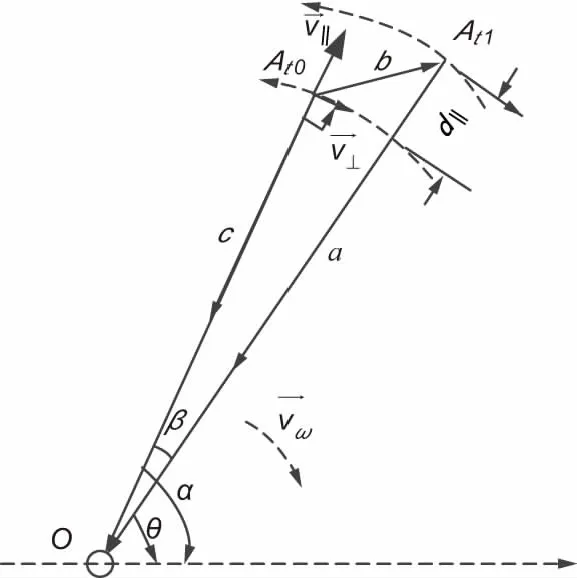
圖2　時差變化率增強單站無源動目標定位模型

在該模型中，角α和θ是動目標t0，t1兩個時刻的方向角，可用θi，i∈Z時刻i的方向角統一表示，角β=α-θ=θi-θi+1=Δθi，i+1代表方向角變化值。顯然有

(3)

即估計足夠高頻度的測向序列值變化率，將收斂于目標運動的切向角度速。

2.2　新算法的流程

時差變化率增強單站無源動目標定位算法的定位模型如圖2所示，其中角度α，β，θ可以通過測向設備測得，d||為由于目標徑向運動分量引起的徑向位移的變化，其求解可以通過周期信號的時差變化率乘以光速求得。因此，只要初始距離c可求，即距離信息加上方向信息可以唯一確定目標的位置。

新模型定位算法流程如圖3所示。先對預求解的目標距離設定t0時刻未知變量c，再按照計算步驟順序，依次開展數據演算估計。

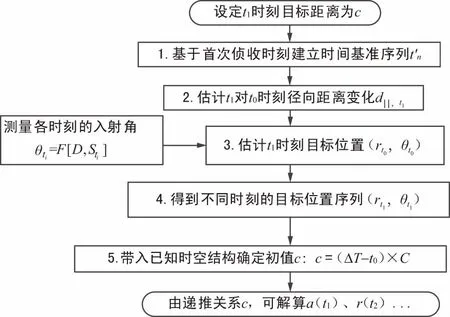
圖3　時差變化率增強單站無源動目標定位算法流程

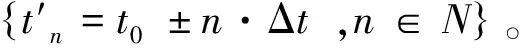
步驟2 顯然當目標的位置與相對距離不發生變化時，偵測站將按以Δt為最小周期的時間序列收到其通信信號。而實際偵收信號時刻偏離時間基準序列就意味著其位置移動和距離(徑向)變化，如式(4)計算相對時差值則可徑向距離的變化量d‖。

DefineΔt′=(t1-t0)-Δt，d‖， t1=Δt′×C。

(4)

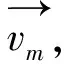
(5)

進而可以計算t1時刻目標的位置(rt0，θt0)=(rt0=c+Δt′×C，θt0)。

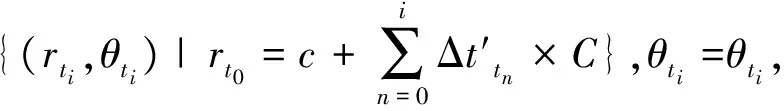
步驟5 很多目標的運動具有固定規律性，這集中表現為其運動過程的起點和終點確知。由此可唯一確定數學模型中的初始/終止距離c/cn，從而確定整個運動過程中的位置。

通過以上估計可得到對t0～tn時刻，運動目標位置距離ci的值，進而實現對運動目標的單站無源定位能力。

在動目標的徑向距離估計研究中，傳統使用多普勒頻率[14]、多普勒變化率[15]和相位差變化率[16]等方法較多。而新方法掌握目標通信信號行為規律，并據此建立的時間基準序列，可以很好地描述目標的電磁信號特征，具有超越傳統信號參數測量上界的性能指標。

2.3　算法定位參數提取

本文所介紹的定位技術主要由測向信息加上距離信息獲得，而距離信息的求解精度依賴于與對目標電磁通信行為規律的掌握所建立的徑向距離變化測量的精度，要由接收系統的信號截獲時間精度所決定。而對于信號檢測處理，理論上界為信號自相關函數，輸出信噪比與信號自身能量相關，是其時寬帶寬積的函數。基于時差的徑向距離高精度估計，歸根到底就是如何高精度地提取信號的到達時間，等價于如何高概率地檢測截獲突發信號。

時差會提高目標徑向的距離測量進度，而系統整體定位的主要誤差來自于單站DOA估計。在雷達、聲納等領域中，對于空間信號到達方向(DOA)估計的研究由來已久。基于陣列天線對DOA估計[17]的方法包括ARMA譜分析、最大似然法、熵譜分析和特征分解法等多種。其中傳統的DOA估計方法，如Capon波束形成法[18-19]，在最小方差法(MVM)優化[20-21]求解后，可得到噪聲與來自非θ方向的任何干擾貢獻功率最小，又能保持θ方向上的信號功率。其估計結果為：

(6)

而MUSIC算法由噪聲特征矢量和信號矢量的正交關系，得到陣列空間譜函數：

(7)

通過對于θ變化，掃描搜索空間中的波峰來估計到達角。而對其在理想情況下，估計誤差協方差矩陣的克拉美-羅界分析有：

(8)

式中，S(i)=diag[s1(i)，s2(i)，...，sK(i)]。另外，噪聲功率的克拉美-羅界為：

(9)

3　仿真對比與分析驗證

3.1　新算法對各種運動規律適應性

本算法由于是對目標結果數據的后處理，且不需要對其運動規律模型的約束，所以算法表現出良好的運動適應性。算法對勻速直線運功的估計效果如圖4所示，觀察點為原點，目標從仰角5°距離10 km外出發，沿x軸做300 m/s的勻速直線運動，在無噪條件下可以達到10-4的定位誤差。仿真顯示將初始距離設為100 km時，其定位誤差也小于10-2m。

(a)定位軌跡線

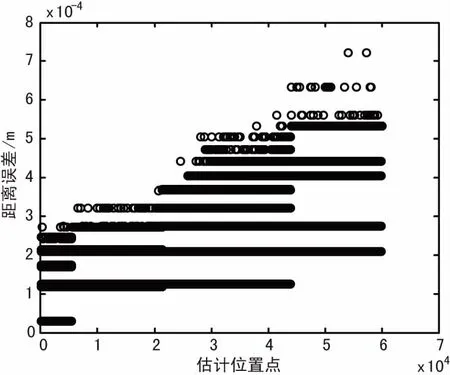
(b)定位軌跡誤差

算法對曲線運功的估計效果如圖5所示，觀察點為原點，目標從仰角5°距離10 km外出發，沿x軸做初速300 m/s加速度仰角2°的曲線運動，在無噪條件下可以達到10-3的定位誤差。仿真顯示將初始距離設為100 km時，其定位誤差也小于10-3m。

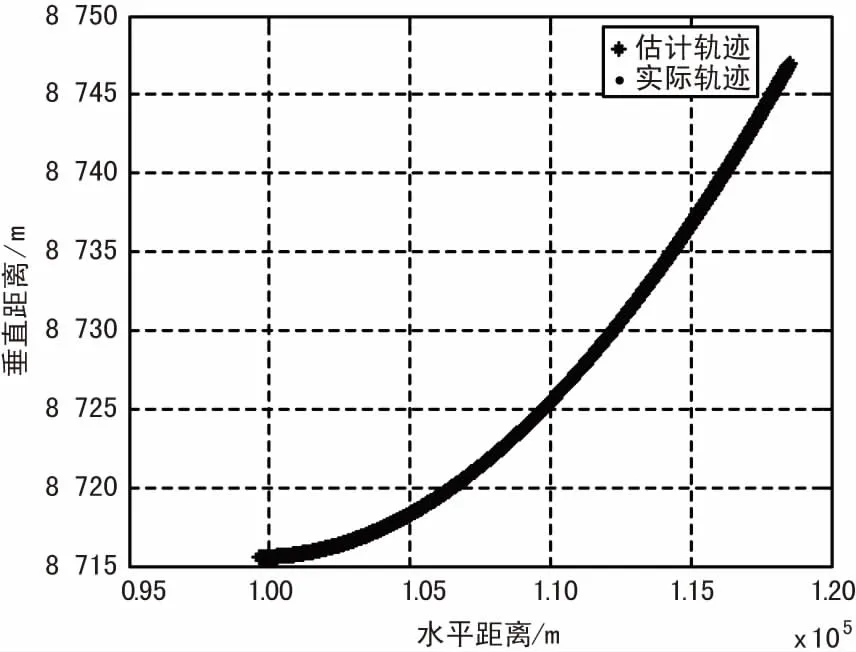
(a)定位軌跡線

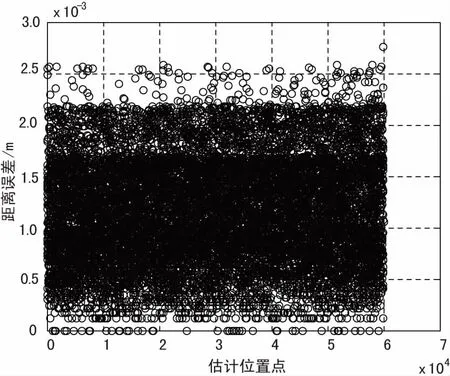
(b)定位軌跡誤差

3.2　新算法對量化誤差和信噪比的適應性

當算法考慮實際信號條件，引入量化誤差和信噪比條件后可得到如圖6所示的仿真結果。當考慮相位量化精度在0.1°，相位測量誤差小于10°，目標距離80 km時典型定位誤差在50 m以內。而當目標距離達到300 km時則達到200 m左右的誤差。

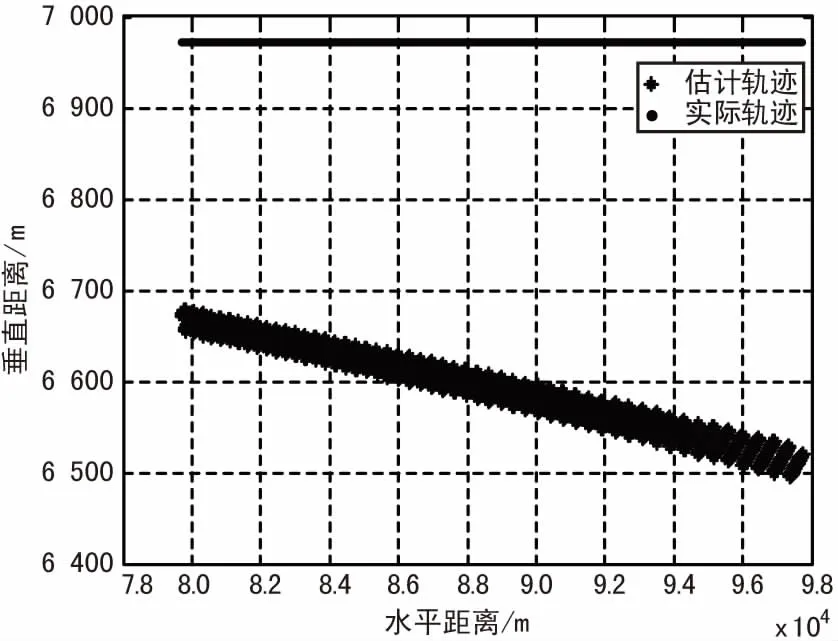
(a)定位軌跡線

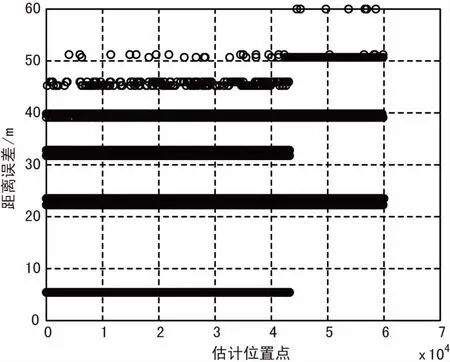
(b)定位軌跡誤差

當算法考慮實際信號條件，引入量化誤差和信噪比條件后可得到如圖7所示的仿真結果。當考慮相位量化精度在0.1°，相位測量誤差小于10°，目標距離80 km時典型定位誤差在100 m以內。而當目標距離達到300 km時則達到400 m左右的誤差上限。

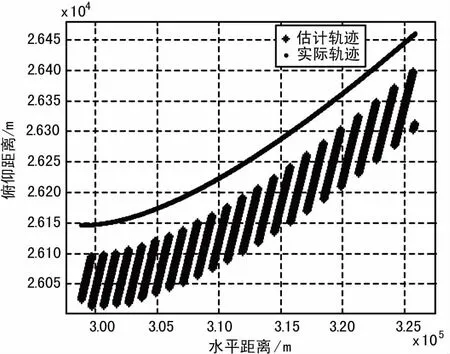
(a)定位軌跡線

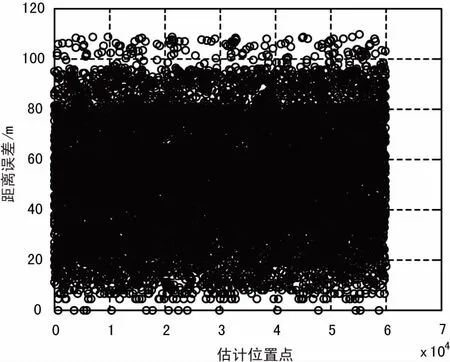
(b)定位軌跡誤差

結合以上仿真可知，新算法對目標的運動狀態沒有依賴，表現出良好的運動適應性，同時再引入量化誤差和信噪比之后，由其所帶來的誤差也控制在1%R(R為偵測距離)之內，在可以容忍的誤差范圍內。

4　結束語

本文方法最大程度地利用了通信類對象在電磁發射行為上的基本規律，將其行為規律轉化為信號分析中的時間性規律，并據此建立模型獲得了超額處理增益。實際的通信系統中有載波同步、幀同步和位同步等結構，其中的時間規律信息都將為分析帶來巨大的收益。此外，對于時間結構周期具體值的估計誤差有隨著時間積累的弊端，在后續的研究使用中應考慮加以改進并克服。

[1]秦軍振.外輻射源雷達系統的測向及定位算法研究[D].西安：西安電子科技大學，2009：1-4.

[2]侍偉偉，胡文，王艷芳，等.基于壓縮觀測的解距離模糊算法[J].數據采集與處理，2013，28(4)：38-40.

[3]CALIKOGLU B.Evaluation and Analysis of Array Anteimas for Passive Coherent Loeation(PCL)Systems[R].Thesis of Air Force Institute of Technology，2002.

[4]韓軍偉.機載單站無源定位技術研究[D].西安：西安電子科技大學，2015：1-14.

[5]李海靜，王立剛.遠程空空導彈機彈協同無源定位技術研究[J].現代防御技術，2016，44(1)：16-21.

[6]胡來招.無源定位技術綜述[J].電子對抗，2004，8(4)：65-70.

[7]張芹.固定單站無源定位系統的可行性研究[D].成都：電子科技大學，2007：1-4.

[8]占榮輝.基于空頻域信息的單站被動目標跟蹤算法研究[D].鄭州：國防科學技術大學，2007：2-12.

[9]應文，李冬海，胡德秀.一種基于時差變化率的單站無源定位方法[J].指揮信息系統與技術，2011，2(1)：27-48.

[10] 應文，李冬海，胡德秀.基于時差和時差變化率的寬帶信號單站無源定位方法[J].電子信息對抗技術，2012，27(2)：14-17.

[11] 李仕云.基于EKF的雙站測向/時差聯合定位算法[J].無線電通信技術，2015，41(1)：38-40.

[12] KANG C W.A Human Motion Tracking Algorithm Using Adaptive EKF Based on Markov Chain[J].IEEE Sensors Journal，2016，16(24)：8953-8962.

[13] 張恒，張迎春.一種動態時分復用方法及FPGA實現[J].無線電工程，2015，45(6)：85-87.

[14] 王鼎，張剛.一種基于窄帶信號多普勒頻率測量的運動目標直接定位方法[J].電子學報，2017(3)：591-598.

[15] 田由甲，張冠杰.基于多普勒頻率變化率的固定單站定位算法研究[J].無線電通信技術，2016，42(4)：61-64.

[16] 高義，高元鋒.基于相位差變化率的無源定位技術研究[J].無線電工程，2013，43(1)：52-55.

[17] 王建英.陣列信號多參量聯合估計技術研究[D].成都：電子科技大學，2000：1-6.

[18] 任曉松，楊嘉偉，崔嵬，等.基于穩健Capon波束形成技術的矢量相關測向方法[J].現代電子技術，2014，37(18)：26-29.

[19] 丁靜.穩健數字波束形成算法研究[J].無線電通信技術，2012，38(6)：30-31.

[20] 廖海軍.一種新的測向交叉定位算法[J].電光與控制，2008，15(9)：29-31.

[21] 王天華.MUSIC算法在無源測向技術中的研究[D].哈爾濱：哈爾濱工程大學，2011：1-7，19-25.