基于混沌Duffing振子的BPSK信號均方值解調方法
蔣亮亮,江 虹,曾 閔
(西南科技大學信息工程學院,四川 綿陽 621010)
0 引言
在數字通信技術領域中,二進制相移鍵控(binary phase shift keying,BPSK)調制信號具有頻帶利用率較高、抗干擾性能較強、硬件易于實現等特點,被廣泛應用于衛星通信、數字電視等通信系統。在數字通信系統中,由于調制信號所處的信道環境日趨復雜,受信道背景噪聲、碼間串擾等因素的影響,接收端的解調誤碼率(bit error rate,BER)較高。因此,在低信噪比(signal-to-noise ratio,SNR)的信道環境下,提升接收端對BPSK信號的解調性能,降低BPSK信號解調誤碼率,對保障通信質量具有重要的意義。
混沌Duffing振子對參數和初值敏感,對噪聲免疫。混沌系統或初值的微小變化會引起系統輸出的較大改變[1];而在噪聲的擾動下,混沌系統能保持自身豐富的動力學特征[2]。這有利于低信噪比環境下弱信號的檢測和處理。為了在低信噪比下,獲得更好的通信信號檢測或解調性能,國內外學者將混沌理論引入信號處理領域。文獻[3]、文獻[4]利用混沌Duffing振子對BPSK信號進行處理,提出均方差算法解調判決,但是對BPSK信號采樣率過大,且沒有考慮到BPSK基帶信號的碼間串擾。文獻[5]、文獻[6]基于參數調整的隨機共振方法對2FSK和4FSK信號進行解調,同樣沒有考慮基帶信號的碼間串擾,且采樣率過大。文獻[7]、文獻[8]研究了極低信噪比下信號的檢測,但檢測的信號是單一頻率的正弦或方波信號。
參考大量文獻后發現,在利用Duffing振子處理信號時,存在以下關鍵問題:一是現有的研究往往利用混沌Duffing振子系統檢測單一頻率或幅值恒包絡信號,即待檢測信號只有1 bit的信息量;二是在采用Duffing振子處理通信信號時,往往未考慮基帶信號波形的成形,即忽略了基帶傳輸過程中必定存在的碼間串擾現象。
針對上述問題,在利用Duffing振子處理BPSK信號時,本文考慮高斯信道傳輸條件下信號的碼間串擾,并設計符合信道傳輸的抗碼間干擾的成形濾波器。結合混沌理論,將Duffing振子應用于BPSK調制信號處理,以提高信號的輸出信噪比;同時,采用均方值(mean square value,MSV)法對BPSK信號碼元進行判決,降低在低信噪比下BPSK信號解調的誤碼率。
1 BPSK原理及混沌Duffing振子
1.1 BPSK信號調制原理
BPSK信號通常用相位0和π表示二進制信息“1”和“-1”。其時域表達式為:
SBPSK(t)=Acos(2πfct+φ)
(1)
式中:A為信號的幅值;fc為載波頻率;φ為相位。
當發送信號“-1”時,φ為π;當發送信號“1”時,φ為0。BPSK信號、碼間串擾、滾降濾波器沖擊響應時域波形如圖1所示。
多數文獻常以圖1(a)、圖1(b)中的BPSK信號為對象進行相關分析。但在實際通信中,由于相鄰碼元會因為拖尾現象的存在導致如圖1(c)所示的碼間相互干擾,故圖1(a)、圖1(b)中的BPSK信號不能作為信息的載體在信道中傳輸。因此,需要對圖1(a)、圖1(b)中的BPSK信號進行成形濾波處理,以消除碼間串擾。
在數字通信中,常用的手段是設計成形濾波器,采用具有低通特性的沖擊響應作為成形濾波器來防止碼間串擾[9]。其表達式為:
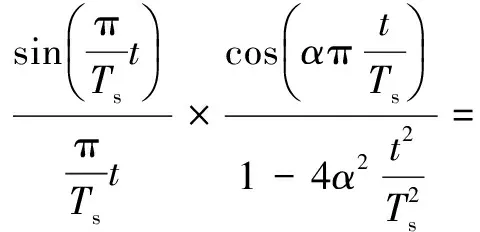
(2)
式中:Ts為時間間隔;α為升余弦滾降系數,且滿足0≤α≤1。滾降系數α分別取0、0.5、0.8、1,得到如圖1(d)中對應的成形濾波器的沖擊響應。
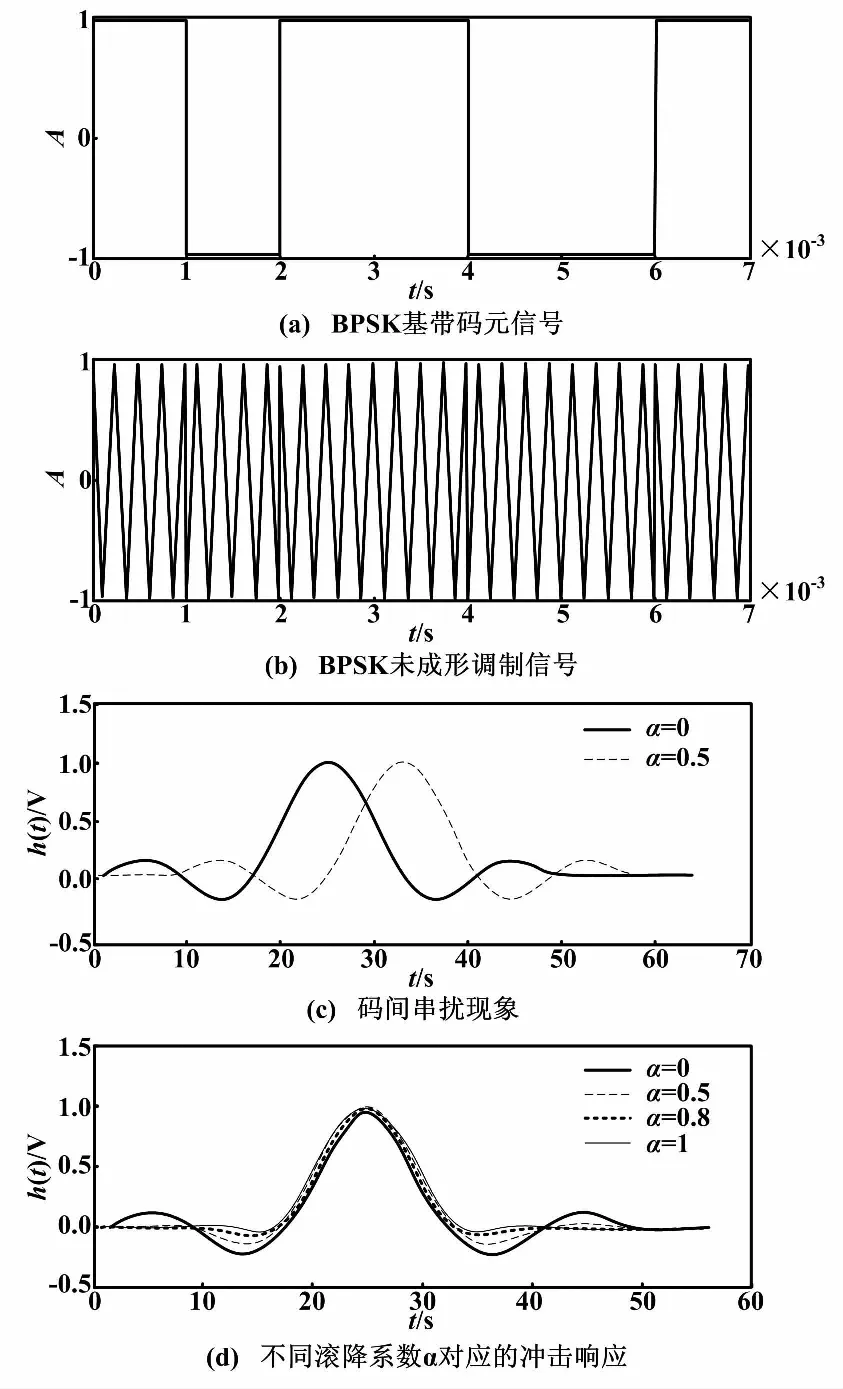
圖1 響應時域波形圖
BPSK滾降調制過程時域波形如圖2所示。
SBPSK(t)=A(t)×cos(2πfct+φ)
(3)
式中:A(t)=a(t)×h(t),a(t)為碼元符號。取20個隨機碼元,其基帶碼元信號幅度為0.1 V,碼元速率RB=1 kBaud,載頻fc=8 kHz,采樣頻率fs=40fc=320 kHz,滾降系數α=0.7。
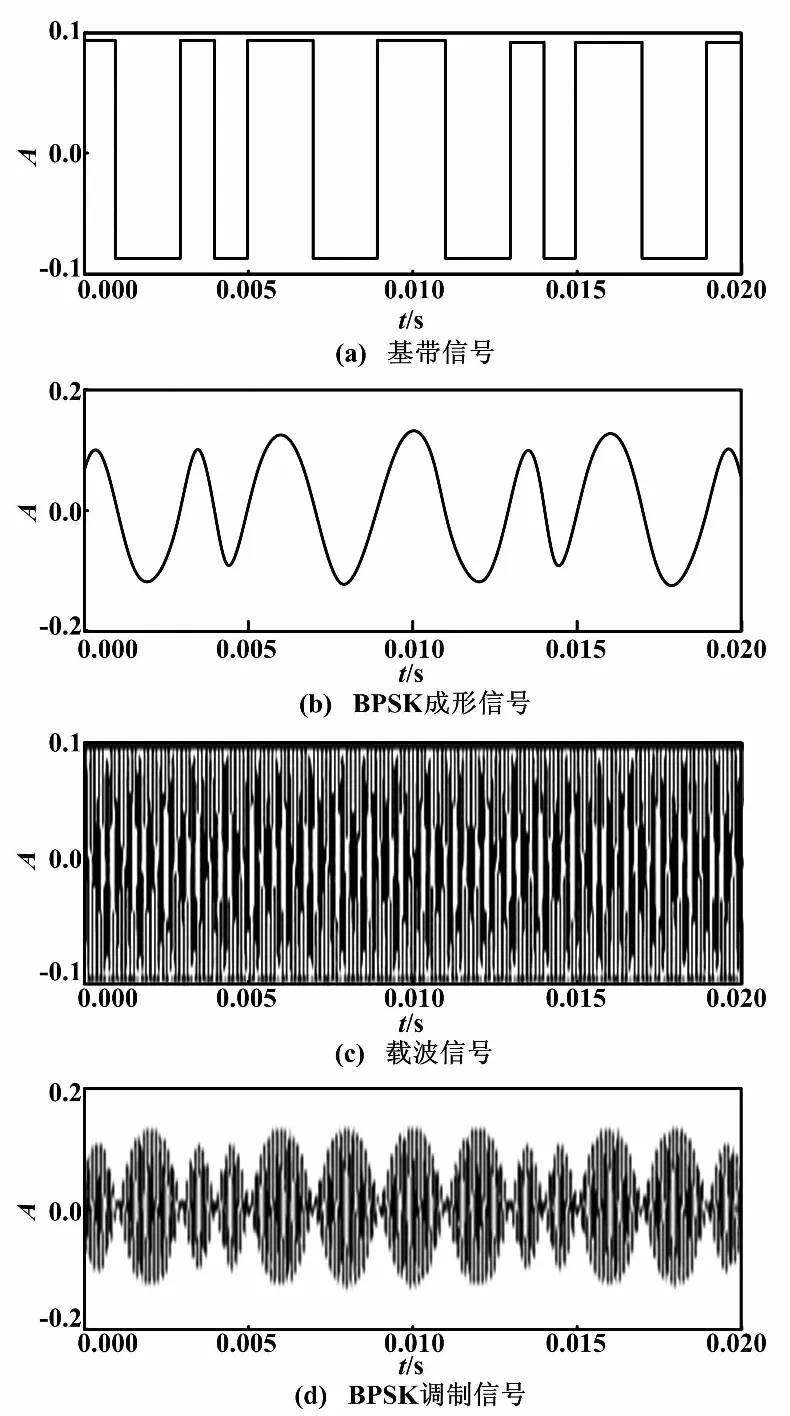
圖2 滾降調制過程時域波形圖
1.2 混沌Duffing振子
在混沌系統中,Duffing振子系統的標準動力學行為方程為:
(4)
式中:x為Duffing振子系統輸出;k為系統的阻尼系數;γcos(2πfct)為Duffing振子的周期策動力;γ為周期策動力的幅值;f(x)為一非線性回復力函數,其表達式為f(x)=-ax+bx3,a和b均為非線性回復力參數[11-12],且滿足a>0、b>0。
故Duffing振子方程具體表達式為:
(5)
也可描述為:
(6)
式中:y為狀態量,在Holmes型Duffing振子系統中,取a=1、b=1,阻尼系數k=0.5[13-14]。
根據Melnikov方法[15-16],γ分別取0.8、0.826和0.83,利用四階龍格-庫塔(Runge-Kutta,R-K)算法[12-13]得到Duffing振子運動的相軌跡圖,如圖3所示。

圖3 相軌跡圖
由圖3可知,隨著周期策動力信號幅度的增加,Duffing振子的相軌跡圖由混沌狀態到臨界混沌狀態,最后到周期狀態[17]。因此,需設置合適的周期策動力信號的幅值(本文設置為0.826)。當加入待測信號時,就可以改變Duffing振子輸出相軌跡的狀態。
將待處理的BPSK信號加入到Duffing振子系統中,式(5)可以寫為:
(7)
式中:sn(t)為經過信道引入噪聲后的BPSK信號,即sn(t)=SBPSK(t)+n(t),n(t)是均值為0、方差為δ2的加性高斯白噪聲。
輸入信噪比可定義為:
(8)
式中:PBPSK和Pn分別為BPSK信號功率和噪聲功率。
當加入BPSK信號時,Duffing系統方程可以寫為:
A(t)×cos(2πfct+φ)+n(t)
(9)
對式(9)化簡得:
γcos(2πfct)+A(t)×cos(2πfct+φ)=
β(t)×cos[2πfct+θ(t)]+n(t)
(10)
其中:
(11)
對于BPSK信號,φ只有0和π兩種取值,即:
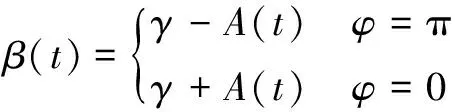
(12)
因此,根據周期策動力信號與BPSK信號疊加后幅度β的變化,Duffing振子的相軌跡處于周期、混沌2種狀態的交替。這2種狀態的交替正是由于BPSK信號碼元信息“-1”和“1”交替引起的。Duffing振子系統相軌跡狀態變化流程如圖4所示。
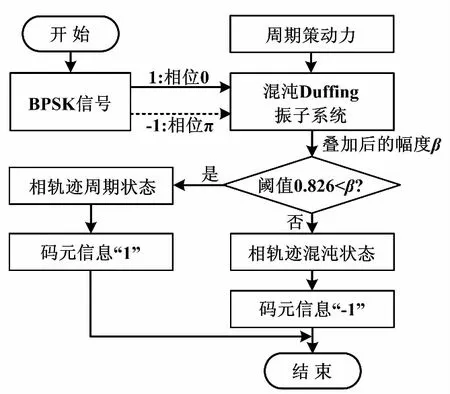
圖4 相軌跡狀態變化流程圖
2 BPSK信號的均方值解調方法
針對Duffing振子系統的輸出,設計一種均方值解調方法。設碼元長度為L,每個碼元上的采樣點數為M,根據四階R-K算法,求得每個碼元時間間隔內的Duffing振子輸出為xi(i=1,2,…,M)。MSV解調方法處理步驟如下。
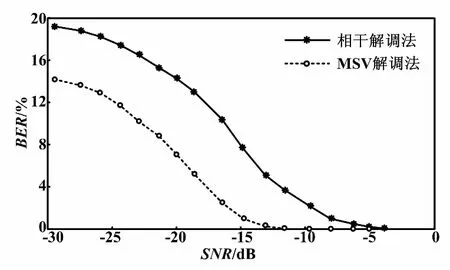
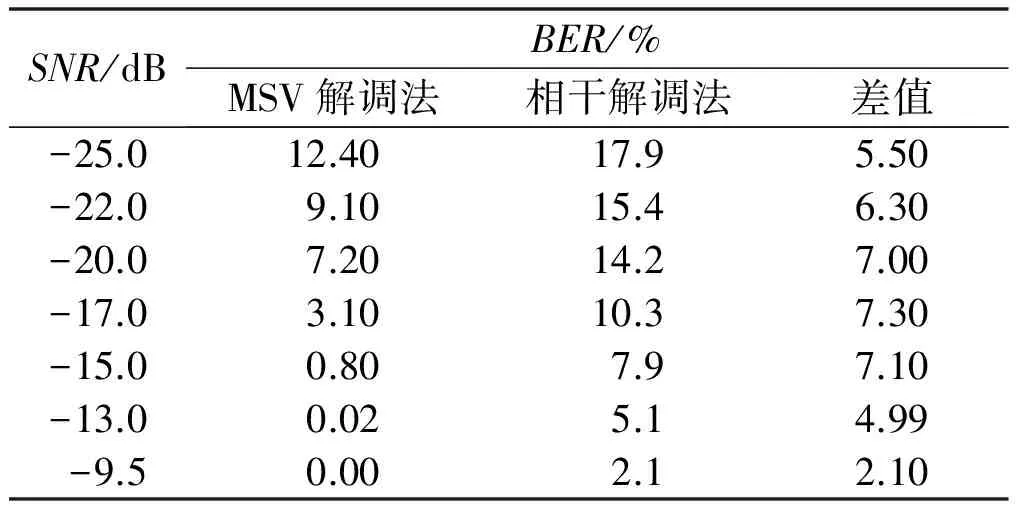
③若Psum>Pavg,判為碼元信息“1”;若Psum 該解調方法復雜度低,計算量小且易于實現。分別取碼元信息“1”和碼元信息“-1”樣本各40個,進行BPSK信號調制,再經過式(9)中的Duffing振子系統處理后,計算均方值,得到如圖5所示的不同SNR下的碼元信息“1”和碼元信息“-1”均方值分布圖。 圖5 均方值分布圖 從圖5以及前文分析可以得出,碼元信息“1”對應Duffing振子輸出均方值明顯高于碼元信息“-1”對應Duffing振子輸出均方值。因此,可以設置閾值進行判決解調。 從圖6可以看出,當信噪比低至-20 dB時,基于混沌振子的MSV解調法解調BPSK信號的誤碼率約為7%,而相干解調法誤碼率為13%;當信噪比為-13 dB時,MSV解調法誤碼率幾乎為0,相干解調法誤碼率為4%左右。本文所提的MSV解調法與相干解調法誤碼率在SNR∈[-25 dB,-15 dB]和SNR∈[-13 dB,-9.5 dB]兩個區間,對比如表1所示。 圖6 誤碼率曲線對比圖 表1 誤碼率對比表 從表1可以看出, MSV解調法在SNR=-20 dB時,解調誤碼率為7.2%;而相干解調法在誤碼率為7.9%時,對應SNR=-15 dB,兩者信噪比相差5 dB以上。MSV解調法在SNR=-17 dB時,解調誤碼率為3.1%;而相干解調法在誤碼率為2.1%時,對應信噪比SNR=-9.5 dB,兩者信噪比相差7 dB以上。由此說明在低信噪比條件下,基于混沌振子的MSV解調法具有更好的解調性能。 在數字通信中,低信噪比環境下BPSK信號解調十分困難。本文研究了一種基于混沌振子理論的均方值解調方法。首先,利用混沌Duffing振子對噪聲的不敏感特性,保證了低信噪比下對BPSK信號的準確檢測;其次,利用Duffing振子對初值的敏感性,設置合適的臨界值γ,當BPSK信號有180°相位突變時,混沌Duffing振子的輸入相軌跡會在混沌狀態和周期狀態之間進行轉變。最后,在高斯噪聲環境下,通過計算分析與仿真結果,表明與傳統相干解調法相比,基于混沌Duffing振子的均方值解調法在低信噪比下具有更好的解調性能。當信噪比低于13 dB時,采用本文方法,誤碼率約為0。 參考文獻: [1] 謝濤,魏學業.混沌振子在微弱信號檢測中的可靠性研究[J].儀器儀表學報,2008,29(6):1265-1270. [2] 范劍.隨機共振和混沌理論在微弱信號檢測中的應用研究[D].天津:河北工業大學,2014. [3] 徐立振.基于混沌理論的微弱BPSK信號檢測技術研究[D].哈爾濱:哈爾濱工業大學,2012. [4] 季錦杰.基于混沌同步的低信噪比BPSK信號接收技術[D].哈爾濱:哈爾濱工業大學,2014. [5] LIU J,LI Z,GAO R,et al.A novel detector based on parameter-induced bistable stochastic resonator for bonary PAM signal processing at low SNR[C].IEEE Communications Letters,2014,18(3):427-430. [6] 王瑞峰,張宏雁.基于Duffing振子的2FSK信號檢測方法研究[J].鐵道學報,2013,35(7):63-67. [7] 路鵬,李月.微弱正弦信號幅值混沌檢測的一種改進方案[J].電子學報,2005,33(3):527-529. [8] 李月,楊寶俊,石要武.色噪聲背景下微弱正弦信號的混沌檢測[J].物理學報,2003,52(3):526-530. [9] 詹亞峰,曹志剛,馬正新.滾降系數誤差對MPSK信號誤碼性能的影響[J].通信學報,2003,24(10):125-130. [10]黃磊,許科,崔慧娟.適用于低滾降系數成型脈沖的定時恢復方案[J].電子技術應用,2011,37(8):117-119. [11]冷永剛,賴志慧.基于Kramers逃逸速率的Duffing振子廣義調參隨機共振研究[J].物理學報,2014,63(2):5021-5029. [12]賴志慧.基于Duffing振子混沌和隨機共振特性的微弱信號檢測方法研究[D].天津:天津大學,2014. [13]王輝武,叢超.一種基于Duffing系統的信號檢測與參數估計新方法[J].電子學報,2016,44(6):1450-1457. [14]李國正,張波.基于Duffing振子檢測頻率位置弱信號的新方法[J].儀器儀表學報,2017,38(1):181-189. [15]WANG G Y,HE S L.A quantitative study on detection and estimation of weak signals by using chaos duffing oscillators[J].IEEE Transactions on Circuits and Systems,2003,50(7):945-953. [16]聶春燕.混沌系統與弱信號檢測[M].北京:清華大學出版社,2009. [17]劉海波,吳德偉,金偉,等.Duffing振子微弱信號檢測方法研究[J].物理學報,2013,65(5):5011-5016.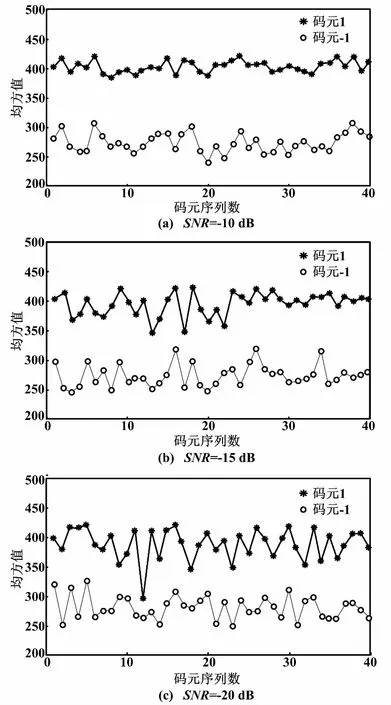
3 結束語

