考慮執行器故障的電動汽車空調魯棒控制

胡廣地,王國暉,羅慧玉,周　柯,郎曉玥

(1.西南交通大學機械工程學院,四川 成都 610031; 2.西南交通大學土木工程學院,四川 成都 610031)

電動汽車空調系統作為電動汽車最主要的電動化附件之一,其性能的好壞直接影響電動汽車的續航里程和乘客乘坐的舒適性.目前,針對電動汽車空調控制系統的研究很多,主要基于傳統控制、智能控制和魯棒控制理論.傳統控制主要包括開關控制、PID控制等.早期Jette等采用開關控制方式對蒸發器出口過熱度進行控制[1]，這種控制方式簡單,但是控制精度很低,容易造成執行器件損壞.Wei等采用PID控制方式對電子膨脹閥和壓縮機的動作進行調節[2]，這種控制方式控制精度更好,但未能充分利用空調系統內部信息,在外部干擾較大時，不能達到理想的控制效果.智能控制在空調制冷系統中的應用主要為神經網絡控制[3-4]，是典型的黑箱建模技術,無需對系統物理意義了解過多,但需要大量的數據才能得到較為精確的數學模型,故市場接受度較低.魯棒控制主要包含有魯棒控制、滑模控制等，Zhang等在汽車空調這一領域的研究較多,對相應的控制指標控制效果較好[5-6].

針對汽車空調系統的故障檢測與控制也已成為國內外一個重要的研究方向.早期的空調故障依賴于簡化模型,這類模型對于空調工況瞬態變化存在嚴重的模型失真[7].任春暉等以故障樹模型研究方法為基礎,對汽車空調在運行過程中的制冷劑不足等問題進行了研究[8]，但其研究主要集中在空調系統的故障診斷,對于系統在出錯狀態下的容錯控制并未做過多探討.國外在汽車空調故障診斷和隔離的研究較多，目前多采用基于觀測器的觀測法和頻域分析法，其中，在觀測器法中,采用H∞濾波器可有效的抑制由系統不確定性和外部干擾所帶來的影響.Zhang等針對執行器中的壓縮機故障、傳感器故障以及參數失真等問題建立了空調系統故障模型,并建立了該模型的輸出反饋控制器[9]，但在執行器故障模型中未考慮膨脹閥以及循環風門發生故障時對系統帶來的影響.本文提出了一種基于執行器故障模型的電動汽車空調系統控制方法，將汽車空調執行器故障按照失效、中斷和偏移等進行分類,在控制器設計中充分考慮上述故障形式,保證系統在部分故障的條件下，依然滿足空調系統性能要求正常工作.

1　電動汽車空調系統數學模型

電動汽車空調系統組成主要由渦旋式壓縮機、冷凝器、膨脹閥和蒸發器組成[10-11]，如圖1所示.

由于電動汽車車廂僅與蒸發器出口狀態參數關系密切,故本文中僅考慮壓縮機、膨脹閥、蒸發器,建立相對應的狀態空間方程，不考慮相鄰相區之間的制冷劑質量流量之間的損耗,得到只包含蒸發器電動汽車空調制冷循環的方程為

(1)

定義：壓縮機輸出轉速為Nc；膨脹閥開度為α；循環風門開度的系統輸入為αin，則有u=(Nc，α，αin)T.換熱模型的詳細描述見文獻[13].

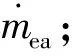
定義：系統輸出為蒸發器壓力為pe；過熱度為SH；蒸發器出口處空氣溫度為Tea,out；相對濕度為ωea,out，則有y=(pe，SH，Tea,out，ωea,out)T.

圖1　電動汽車空調系統模型Fig.1　Electric vehicle air conditioning system model

為了便于進行控制器設計,將式(1)在空調的工作點附近進行局部線性化處理.其中，最主要是需對Ze(xe)進行線性化處理[14].選擇系統的工作點(xe,ue,we)，其中：根據文獻[5]中Ze(xe)的格式，可知在其工作點Ze(xe)的滿秩矩陣,進而可得動態擾動模型為

(2)

式中:δx=x-xe；δu=u-ue；δw=w-we；xe、ue、we分別為穩定狀態時狀態向量、控制輸入和擾動.

根據系統穩態工作點(xe,ue,we),可以得到狀態矩陣的偏導關系式為

(3)

記

同時，對y=g(x)在其工作點進行局部線性化處理,則可以得到線性模型為

(4)

2　汽車空調執行器故障模式分析

執行器在故障條件下，空調系統輸入為[15]

uF(i,j,t)=m(i,j,t)u(i,t)

+σ(i,t)us(i),

(5)

式中:uF(i,j,t)為第i個執行器在第j種故障模式在時刻t時的被控輸入;m(i,j,t)為執行器第i個執行器在第j種故障模式下的效率因子;u(i,t)為第i個執行器的被控輸入;σ(i,t)為第i個執行器在第j種故障模式下偏移或卡死的常數因子;us(i)為第i個執行器偏移或卡死的被控對象常值輸入.

相應的故障模式如表1所示[16].

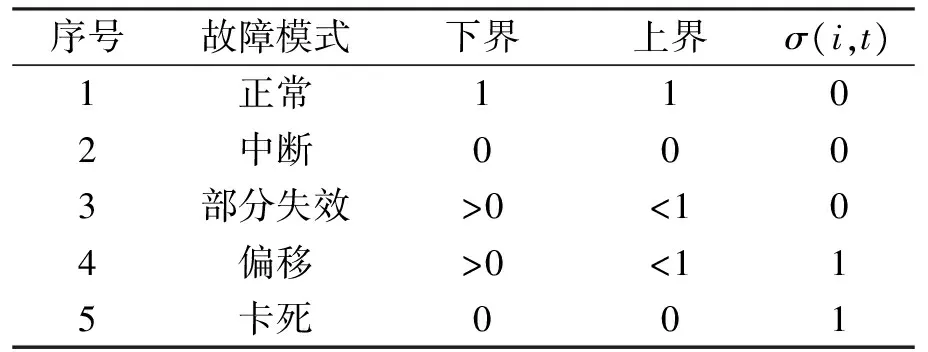
表1　故障模式Tab.1　Failure mode

對于實際的空調系統,由于膨脹閥開度以及循環風門開度最大開度均為100%,根據表1所述偏移故障的定義,這兩個執行器均不可能出現開度大于100%的情況,即這兩個控制器均不會出現偏移故障.為便于描述,將式(5)簡寫為

uF(t)=m(t)u(t)+σ(t)us.

(6)

由式(6)可知,若壓縮機輸出轉速、膨脹閥開度以及循環風門開度中某一個或某幾個發生部分失效、偏移、卡死或者中斷等問題時,即可判定為執行器故障.將式(6)代入式(4)，得到包含有執行器故障模式的電動汽車制冷系統的狀態方程為

(7)

本文的控制任務是對式(7)所述帶有執行器故障的電動汽車空調制冷循環系統,考慮系統的擾動和執行器擾動,設計狀態反饋控制律u(t),消除執行器故障和擾動對系統穩定性所帶來的影響.

3　考慮執行器故障的H∞狀態反饋控制器設計

3.1　狀態觀測器的設計

電動汽車空調制冷系統中，狀態變量如兩相區長度、過熱區出口焓值等不能直接測得，需要對其狀態進行觀測.本文采用狀態觀測器對制冷空調系統狀態變量進行觀測.

構造線性化后模型(1)的開環狀態觀測器為

(8)

引入觀測矩陣L,則狀態觀測方程為

(9)

定義真實狀態和估計狀態的誤差向量為e,則有

當(Aac-LCac)的特征值有負實部時,狀態向量誤差按照指數衰減,即

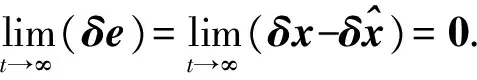
(10)

3.2　反饋控制器的設計

將式(7)簡化為

(11)

式中:

δ(t)=σ(t)urs.

由于

diag{m(1,t)-1,m(2,t)-1,m(3,t)-1}

m(i,t)∈[0,1],i=1,2,3.

針對式(7)設計狀態反饋控制器為

(12)

式中:Kac為一常數矩陣,使得對于所有的故障模式,閉環系統是二次穩定的,滿足

(13)

式中：yr(t)為系統輸出；γ為穩定裕度系數；ωr(t)為擾動.

由于δ(t)=σ(t)us,一般地,控制器輸出是有限制的,即:umin≤us≤umax,故存在常值矩陣Θ,使得

(14)

關系成立.

(15)

引理1[16]對于任意具有適當維數的矩陣H、F(t)、E,其中，F(t)滿足FT(t)F(t)≤E,則對于任意的ε>0,有

HF(t)E+ETFT(t)HT≤

ε-1HHT+εETE.

(16)

不考慮干擾輸入的作用,將式(12)代入式(11)得到閉環系統，即

(17)

類似式(17)這樣的系統是二次穩定的.

(18)

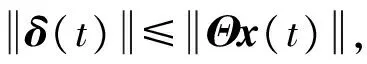
定義

Q=(Aac+Bac2Kac)T+P(Aac+Bac2Kac)+

(Bac2Θ)TP+P(Bac2Θ)+

則有

(19)

即當Q<0時,則閉環系統(17)二次穩定.根據引理1,可知,對于給定的ε>0,有

(Bac2Θ)TP+P(Bac2Θ)≤

則有

Q≤Q0=(Aac+Bac2Kac)TP+P(Aac+Bac2Kac)+

(20)

若使Q<0,只需要Q0<0，則

(21)

式中:λmax(Q0)為矩陣Q0的最大特征值.

取α=-λmax(Q0),即可保證閉環系統(式(17))是二次穩定的.

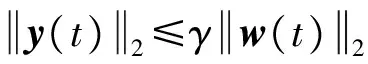
定義泛函指標

(22)

上述證明可知式(17)是二次穩定的,定義為

(23)

根據上述證明可以得到對于任意非零干擾w(t)有

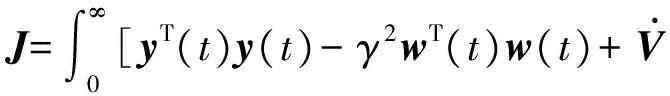
γ2wT(t)w(t)+K(x,t)]dt.

(24)

根據引理1,有

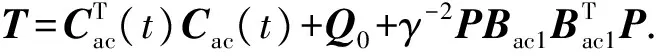
式(24)可簡化為

(25)

當T<0,可保證y(t)滿足H∞性能約束.

進一步利用Schur補原理，并取

Z=KacP-1，

X=P-1.

可將T<0等價為LMI問題，有

(26)

故若存在正定對稱矩陣X和矩陣Z使得上述線性矩陣不等式成立,求得的控制器增益Kac=ZX-1,使得系統不僅二次穩定,而且滿足H∞的性能要求.所求得的狀態反饋控制器為

(27)

式(27)即為該系統考慮系統擾動和執行器故障的狀態反饋輸出控制器.

4　仿真對比分析

電動汽車空調系統各狀態參數穩態工作點如表2所示[5].

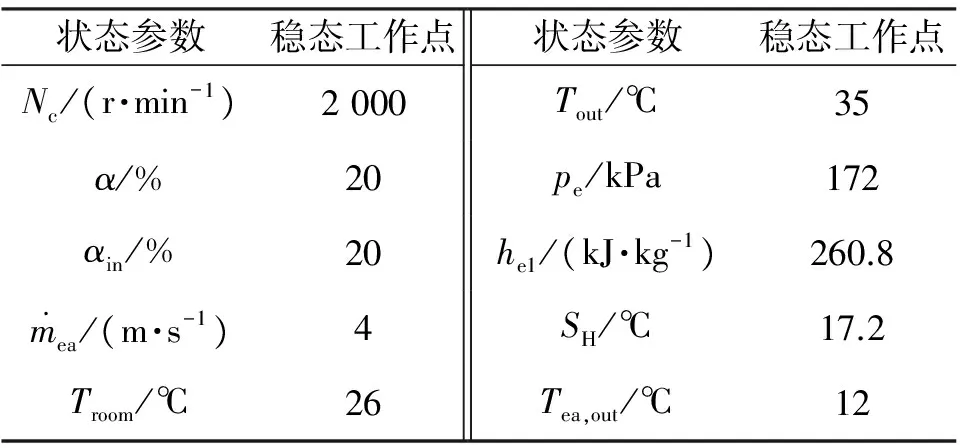
表2　各狀態的穩態工作點Tab.2　Static working point of each state

通過對模型進行線性化處理,得到電動汽車空調制冷循環方程為

通過極點配置的方法對該系統進行狀態觀測器的設計,所得到的狀態觀測器觀測矩陣為

通過采用LMI對模型進行仿真,得到控制器

為不失一般性,本文對一般故障模式進行仿真實驗.即第1個控制器輸出偏移,第2個控制器部分失效,第3個控制器輸出卡死,且在卡死狀態控制器輸出為控制器輸出最大值.

4.1　輸入干擾抑制能力分析

分別對原系統、采用一般H∞魯棒控制原理所設計的控制器、考慮執行器故障時所設計的H∞魯棒控制器的幅頻特性進行分析.

對于幅頻特性曲線,當其幅值大于0時,對輸入端所產生的干擾并無抑制效果,當其幅值小于0時,其幅值越小,對輸入端所產生干擾的抑制能力就越好.圖2為各系統3個輸入對各個輸出的幅頻特性曲線.由于汽車空調系統變化相對較慢,在這里主要考慮其低頻段和中頻段的性能.

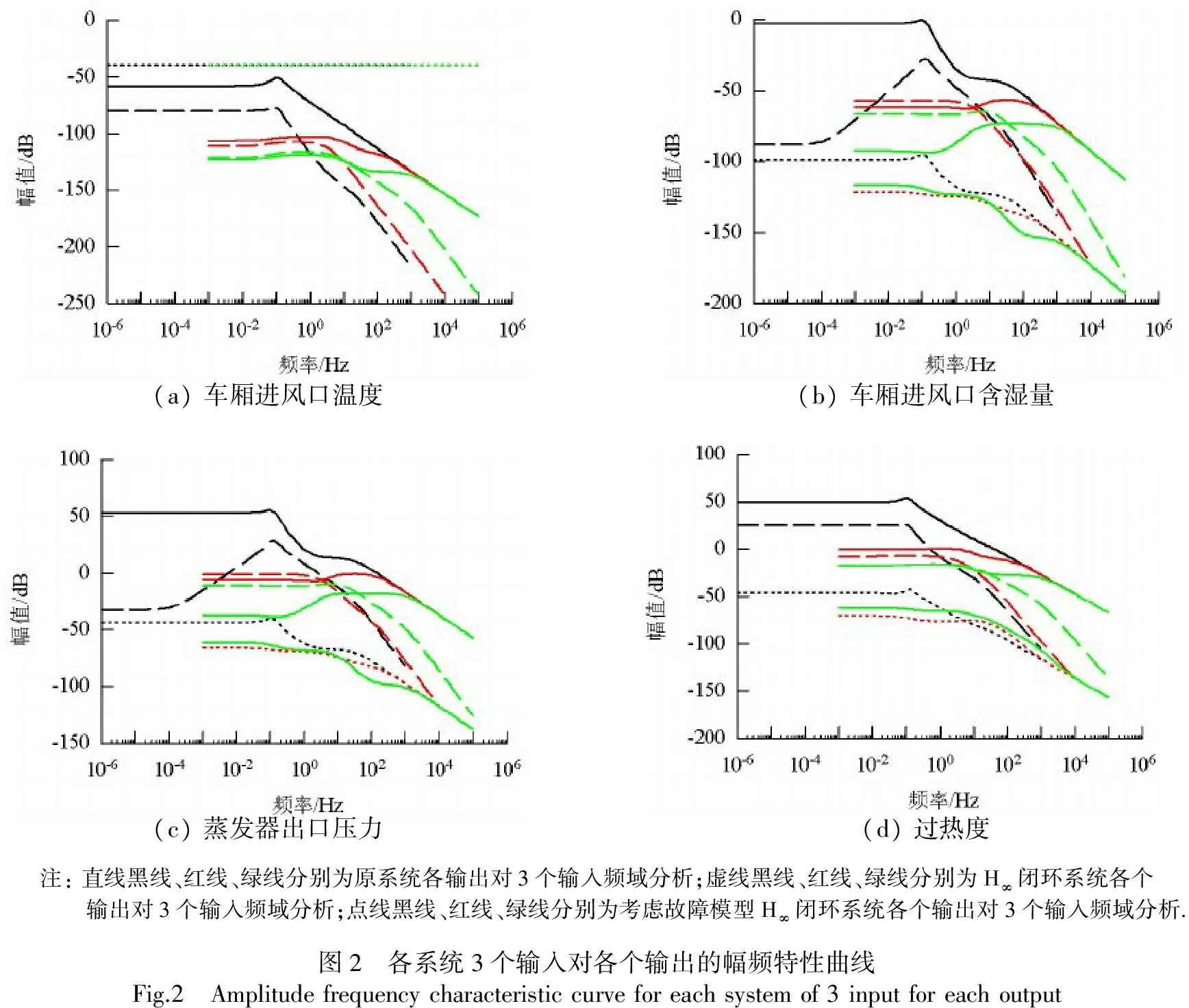
(a)車廂進風口溫度(b)車廂進風口含濕量(c)蒸發器出口壓力(d)過熱度注：直線黑線、紅線、綠線分別為原系統各輸出對3個輸入頻域分析；虛線黑線、紅線、綠線分別為H∞閉環系統各個輸出對3個輸入頻域分析；點線黑線、紅線、綠線分別為考慮故障模型H∞閉環系統各個輸出對3個輸入頻域分析．圖2　各系統3個輸入對各個輸出的幅頻特性曲線Fig．2　Amplitudefrequencycharacteristiccurveforeachsystemof3inputforeachoutput

由圖2可知,在低頻段和中頻段,在多數情況下，采用容錯H∞魯棒控制器閉環系統的幅值小于采用魯棒控制的閉環系統,且均優于原系統.這表明,容錯H∞魯棒控制器對輸入端的干擾抑制能力更強.

4.2　仿真結果分析

由圖3的仿真結果可以看出,基于狀態觀測器的容錯控制器在有故障條件和無故障條件下，各個輸出的相對誤差很小,可以滿足系統對觀測誤差性能的要求.

本文式的故障結構為

(28)

對式(28)的仿真結果如圖4所示.此時，采用一般H∞魯棒控制方法所設計的控制器在各個輸出，無論是響應速度，還是超調量，均不及考慮執行器故障時的H∞魯棒控制閉環系統穩定.

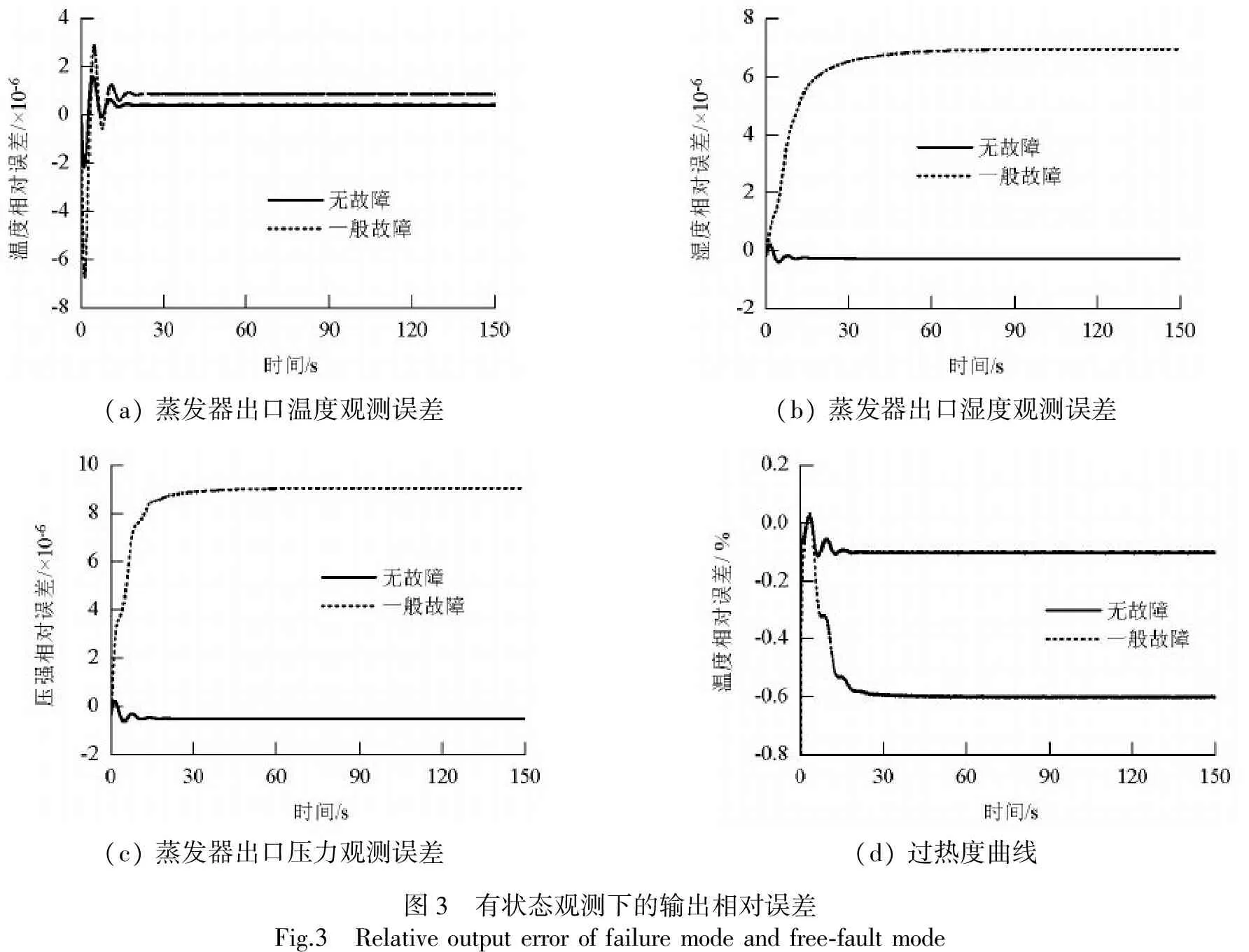
(a)蒸發器出口溫度觀測誤差(b)蒸發器出口濕度觀測誤差(c)蒸發器出口壓力觀測誤差(d)過熱度曲線圖3　有狀態觀測下的輸出相對誤差Fig．3　Relativeoutputerroroffailuremodeandfree?faultmode

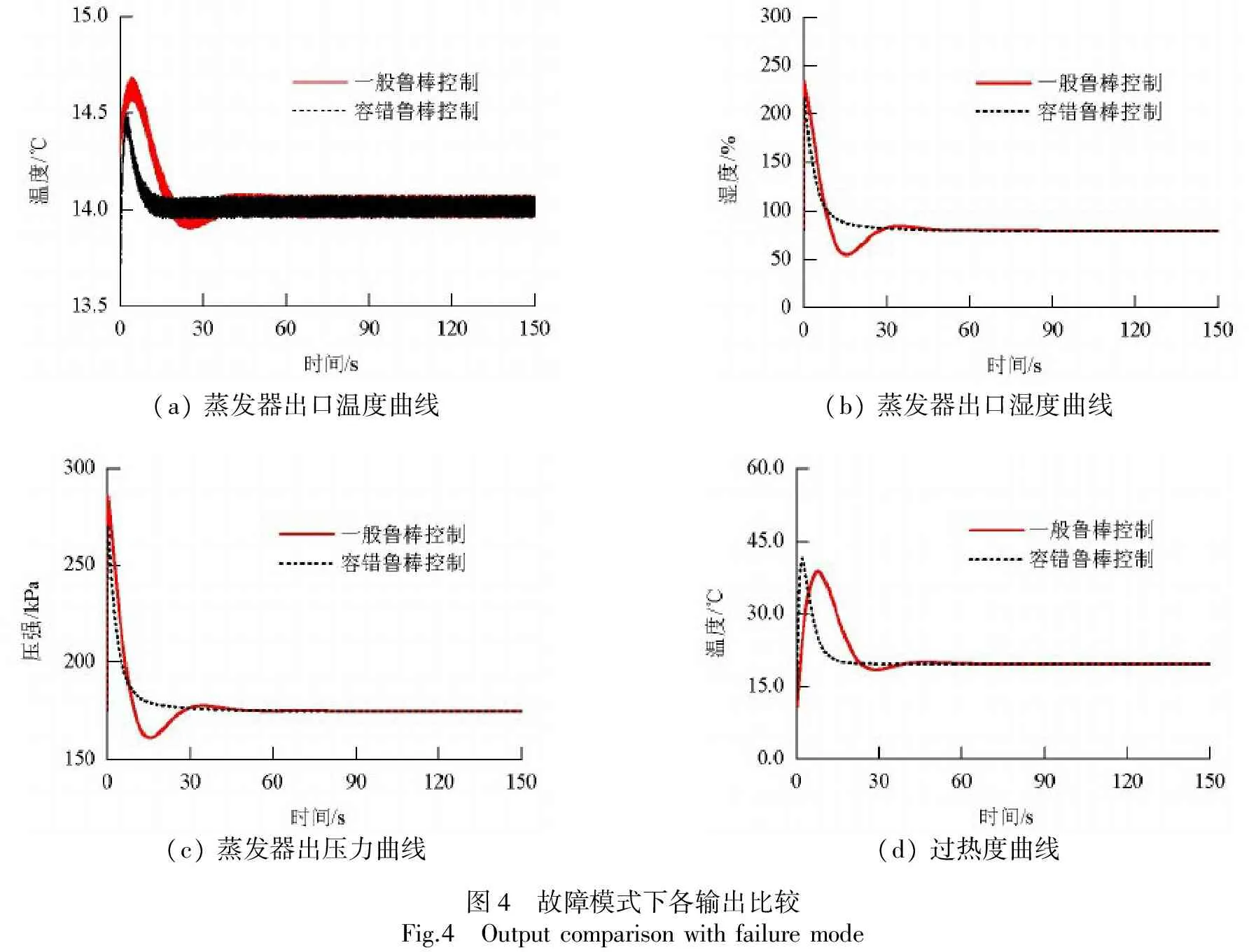
(a)蒸發器出口溫度曲線(b)蒸發器出口濕度曲線(c)蒸發器出壓力曲線(d)過熱度曲線圖4　故障模式下各輸出比較Fig．4　Outputcomparisonwithfailuremode

5　結　論

針對電動汽車空調系統,建立了基于觀測器的電動汽車空調系統，依據其執行器發生故障的模式,提出了汽車空調故障模型的H∞魯棒控制器.充分考慮了執行器在系統運行過程中可能存在的失效、中斷和偏移等問題,將故障模型化為系統的不確定性模型.通過采用線性矩陣不等式(LMI)工具設計對考慮執行器故障的H∞狀態反饋魯棒控制器進行設計,并且證明了閉環系統的穩定性.仿真結果表明:在有故障和無故障模式下的觀測誤差最大分別為0.1%和0.6%，滿足系統的觀測需求；與未考慮執行器故障的電動汽車空調H∞控制器相比，在10 Hz以下頻段，考慮執行器故障的H∞控制方式可有效地抑制系統輸入端所帶來的干擾.

參考文獻:

[1]JETTE I,ZAHEER-UDDIN M,FAZIO P.PI-control of dual duct systems:manual tuning and control loop interaction[J].Energy conversion and management,1998,39(14):1471-1482.

[2]QIAN W,PENG F Z,CHA H.Trans-z-source inverters[J].IEEE transactons on Power Electronics,2011,26(12):3453-3463.

[3]付龍海,李蒙.基于PID神經網絡解耦控制的變風量空調系統[J].西南交通大學學報,2005,40(1):13-17.

FU Longhai,LI Meng.Variable-air-volume air-conditioning system based on PID-ANN decoupling control technology[J].Journal of Southwest Jiaotong University,2005,40(1):13-17.

[4]HOSOZ M,ERTUNC H M.Artificial neural network analysis of an automobile air conditioning system[J].Energy Conversion and Management,2006,47(11):1574-1587.

[5]ZHANG Q,CANOVA M.Modeling and output feedback control of automotive air conditioning system[J].International Journal of Refrigeration,2015,58:207-218.

[6]ZHANG Q,CANOVA M,RIZZONI G.Sliding mode control of an automotive air conditioning system[C]∥American Control Conference.[S.l.]:IEEE,2013:5748-5753.

[7]KEIR M C,ALLEYNE A G.Dynamic modeling,control,and fault detection in vapor compression systems[R].[S.l.]:University of Illinois at Urbana-Champaign,2006.

[8]任春暉.基于故障樹分析的汽車空調系統故障診斷研究[J].中國農機化學報,2013,34(5):182-184.

REN Chunhui.Research of A/C Fault diagnosis based on failure tree analysis[J].Journal of Chinese Agricultural Mechanization,2013,34(5):182-184.

[9]ZHANG Q,CANOVA M.Fault detection and isolation of automotive air conditioning systems using first principle models[J].Control Engineering Practice,2015,43:49-58.

[10]劉占峰,宋力,趙丹平.汽車空調[M].北京:北京大學出版社,2011： 22-65.

[11]吳偉軍,鐘建法,彭仟能.并聯渦旋式壓縮機在空氣源熱泵機組中的應用分析[J].制冷與空調,2013(1):55-58.

WU Weijun,ZHONG Jianfa,PENG Qianneng.Application analysis of parallel scroll compressors for air-source heat pump chiller[J].Refrigeration and Air Conditioning,2013(1):55-58.

[12]MCKINLEY T L,ALLEYNEA G.An advanced nonlinear switched heat exchanger model for vapor compression cycles using the moving-boundary method[J].International Journal of Refrigeration,2008,31(7):1253-1264.

[13]FARZANEH Y,TOOTOONCHI A A.Intelligent control of thermal comfort in automobile[C]∥ 2008 IEEE Conference on Cybernetics and Intelligent Systems.[S.l.]:IEEE,2008:510-514.

[14]YANG Xiaozheng,YANG Guanghong.Robust adaptive fault-tolerant compensation control with actuator failures and bounded disturbances[J].Acta Automatica Sinica,2009,35(3):305-309.

[15]陳躍鵬,周祖德.廣義系統的魯棒控制與容錯控制[M].北京:科學出版社,2010:41-46.

[16]金小崢,楊光紅,常曉恒,等.容錯控制系統魯棒H∞和自適應補償設計[J].自動化學報,2013,39(1):31-42.

Jin Xiaozheng,Yang Guanghong,Chang Xiaoheng,et al.Robust fault-tolerant control with adaptive compensation[J].Acta Automatica Sinica,2013,39(1):31-42.