基于殘差卡方檢驗和動態Allan方差的INS/GPS故障檢測與定位算法研究
張春熹,盧 鑫,高 爽,王 璐
(北京航空航天大學儀器科學與光學工程學院,北京 100191)
0 引言
一般的慣性導航系統通常由兩種傳感器組成,即沿正交方向的3軸陀螺和3軸加速度計,并通過與衛星、磁強計等外部信息的組合,提供精確可靠的導航數據。而慣性傳感器作為INS的核心器件極易受到外界的干擾,造成INS性能的下降,包括零偏和標度因數等參數都會受到影響,可能短期內就會在姿態、速度、位置中累積巨大的誤差[1]。因此,需要對INS的工作狀態進行實時的監控,當其出現故障時及時報警。
一般來說,故障可分為硬故障和軟故障。硬故障主要通過BIT(Built In Test)來檢測[2];軟故障可以認為是由于環境等因素造成的慣性器件的性能下降即傳感器信號中的未知改變,及由于衛星信號受到干擾、遮擋或載體高動態運動造成的衛星數據的不確定性。這類故障通常表現為陀螺或加速度計出現異常的偏值,輸出噪聲特性發生變化或者衛星信號中夾雜有額外地噪聲等[3]。
在系統層面進行故障檢測時,通常使用卡方檢驗法作為故障檢測算法,這種方法一般是使用狀態評價器并構建統計學方程來進行系統層面的狀態監測[4]。這時由環境干擾等造成的傳感器性能的改變及用于組合導航的外部信息的故障都會耦合進入統計特性中,因此使用卡方檢驗法可以對整個慣導系統的工作狀態進行實時的監控,當出現故障時及時報警,然而該方法并不能夠準確地識別出故障發生的位置。
要想實現對故障的準確定位,需要一種能夠在傳感器層面進行故障檢測的算法。一般來說,為了分辨和評價慣性傳感器的噪聲特性,通常使用功率譜密度(PSD)、均方根(RMS)、Allan方差等方法,這些方法都是以統計學的方法分析當前數據,判斷傳感器的工作狀態,并對未來可能出現的特性改變做出預測和辨識[5]。其中以Allan方差法最具代表性,作為IEEE協會認可的一種評價陀螺性能的方法,被廣泛應用于各種慣性傳感器性能的評估。由于實際的傳感器故障信號可能會在短時間內表現出不穩定性,且長時間內被測信號可能會受到由于環境變化、自身老化或突然故障造成的自身性能下降的影響,傳統Allan方差法的使用受到了極大的限制。動態Allan方差法的出現使得跟蹤和描述信號隨時間變化的特性和各種噪聲系數成為可能[6],然而這種方法的問題在于計算量很大,這對于小型化的導航計算機來說是一個巨大的負擔,無法保證故障檢測的實時性。
所以必須綜合利用系統級和傳感器級的故障檢測方法,充分發揮各方法的優勢,實現對故障的及時檢測和準確定位。
1 原理
1.1 基于殘差卡方檢驗法的系統故障檢測
卡方檢驗是判斷統計樣本的實際觀測值與理論值之間偏離程度的一種方法,實際觀測值與理論值之間的偏離程度越大,則卡方值越大。
根據所構造的隨機向量的不同,卡方檢驗法又可分為殘差卡方檢驗法和狀態卡方檢驗法[7]。狀態卡方檢驗法在報警期間沒有漏檢,但因其計算量大,報警延遲高,而且靈敏度隨著濾波的不斷進行有所下降;而殘差卡方檢驗法報警延遲小,對量測故障比較敏感,可以直接使用Kalman濾波器的計算結果從而運算量較低,是最為廣泛使用的故障檢測算法。
殘差卡方檢驗法一般有兩個步驟,首先是通過Kalman濾波的新息迭代來提供待檢測信號,然后再使用閾值函數來界定故障和干擾。故障檢測算法的設計就是要盡量將干擾的影響降至最低,并盡最大可能分辨出故障的發生[8]。
一般基于松組合的INS/GPS系統的狀態變量可以表示為:
Xk=[θTδvTδpTεTT]T
(1)
狀態方程可以寫為:
Xk+1=FkXk+Gkωk
(2)
Fk為系統的狀態轉移矩陣,ωk為系統的噪聲過程,Gk視作白噪聲且其方差陣為一常值,為系統的噪聲轉移矩陣。
量測向量及觀測方程為:
Yk=[(v-vGPS)T(p-pGPS)T]T
(3)
Yk=HkXk+vk
(4)
Yk為INS和GPS的速度和位置差,Hk為觀測系數矩陣,vk為觀測噪聲并假設其為白噪聲過程。
在k時刻得到的Kalman濾波狀態估計方程為:
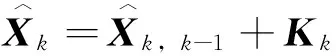
(5)
一旦傳感器或外部信息即觀測值出現故障,都會與之前的假設ωk和vk為相互獨立的白噪聲相矛盾。當系統正常工作未出現故障時,rk應該是Gauss白噪聲服從0均值方差vk的正態分布,且不同時刻的新息向量相互獨立:
rk=Yk-HkXk,k-1~N(0,Vk)
(6)
Vk=HkPkHkT+Rk
(7)
為了檢測出這時噪聲方差陣的改變,需要構建一個合適的統計學方程,選擇數據窗口長度為p,即截取p個新息的樣本數據作為一組,則其總體服從自由度為6p的卡方分布。觀察系統模型方程和Kalman濾波的迭代方程,評價函數可以設計為:
(8)
接下來選擇相應的顯著性水平為a(0 (9) 這里根據自由度6p和系統要求的虛警率參照卡方分布表來選取合適的閾值ε,當評價函數大于閾值時,說明系統有故障發生,否則系統正常工作,即: 通過不斷地對評價函數值與閾值進行比較,可以實現實時的故障檢測。 Allan方差法是一種時域的分析方法,可以將傳感器隨機模型中的噪聲項量化成偏值不穩定性、角度隨機游走、量化噪聲等[9]。傳統的Allan方差是以采樣周期τ0對陀螺輸出的角增量進行采樣,在連續采樣N個數據點后,將其分為K組,每組包含M(M<(N-1/2))個采樣點,每組數據的持續時間為τ=Mτ0,即相關時間。 不同的分組方式對應每一組的平均值為: (k=1,2,…,K) (10) 則Allan方差的計算公式為: (11) 根據不同相關時間對應的不同Allan方差值,可以繪制出它們的雙對數曲線圖,并通過其與原始數據中噪聲功率譜對應的關系,借由曲線擬合得到不同的噪聲系數,此時Allan方差可以表示為幾種誤差源方差的平方和: (12) 相應的噪聲系數N、K、B、Q、R分別代表角度隨機游走、速率隨機游走、零偏穩定性、量化噪聲、速率斜坡5種噪聲源的系數,其計算公式為[10]: (13) 動態Allan方差是經典Allan方差的擴展,它的基本思路是分別計算信號在不同時段內的Allan方差,并將計算結果繪制在同一幅3維圖中。其計算方式為定義窗口長度為M的窗函數PL(t′),步進長度N(N y(t,t0)=x(t0)PL(t-t0) (14) 假設待處理的樣本總長度為L,則y(t,t1)由長度為M的采樣信號組成,對這段信號進行Allan方差分析,隨后依次步進至t0+kN(k=1,2,…)點作為下一組待處理樣本的中點,繼續進行Allan方差分析,最后將所有的分析結果以x軸、y軸和z軸分別代表時間、相關時間、Allan方差值的關系繪制在3維坐標系中,就可以得到這段樣本的動態Allan方差分析圖,并可以分別計算出每次步進后該組樣本的噪聲系數。 從圖1、圖2可知,排除500s~600s的GPS故障和1000s~1200s的傳感器故障外,系統運行穩定,3軸速度誤差幾乎為0,且評價函數的值一直維持在一個較低的水平即小于20;而在500s~600s時由于GPS信號受到干擾,速度誤差值顯著增加,評價函數值也隨之出現了劇烈的跳變;而在1000s~1200s時,由于慣性傳感器輸出的噪聲參數發生改變,影響了濾波新息的卡方分布,造成了評價函數的突變,而且由于Kalman濾波器所建立的噪聲模型與傳感器真實的噪聲模型存在巨大偏差,故濾波器一直無法收斂,導致評價函數的值一直無法達到一個比較小的水平,即系統一直處于故障的狀態,速度誤差圖反映的情況基本與故障發生的情況相符,1200s后傳感器和GPS恢復正常狀態,系統又回到正常工作狀態。 隨后對實驗2系統故障時的運行數據進行動態Allan方差分析,計算條件選擇矩形窗,并將窗口長度設置為50s,窗口中點的步進長度為16s,擬合方式選擇最小二乘擬合,具體對比如圖3、圖4所示。 由于卡方檢驗已經將故障出現的時間段確定在600s~700s和1000s~1200s之間,接下來需要確定故障出現的位置,僅需在故障發生前后的局部區域對不同傳感器進行動態Allan方差分析即可,故選擇500s~800s及950s~1250s的傳感器數據進行動態Allan方差分析,即圖3中的0s~300s。由圖3(a)可知,950s~1250s的Allan方差分析圖出現了明顯的波動,這是其中一段數據加速度計出現了故障導致的,故障時的噪聲系數也明顯增大;而由圖3(b)可知,正常工作的傳感器的Allan方差分析圖非常平穩,且噪聲系數保持在一個平穩的范圍內,由此可以判斷此次故障應該是由GPS信號的異常造成的。 由于慣性傳感器可能受到復雜外界環境的干擾,不失一般性選用實際采集的振動條件下的INS的數據進行故障檢測算法分析,卡方檢驗的結果如圖5所示。 圖5中可見在0s~300s評價函數值非常小,說明系統在該時間段工作正常未出現故障,而在300s~600s評價函數出現了不平穩的現象,且在600s~700s時出現劇烈波動,并在1000s后恢復正常,說明INS系統在300s~1000s的時間段內非正常工作。 隨后對故障出現的200s~1100s的任意一軸陀螺數據進行動態Allan方差分析,數據采樣間隔2.5ms,數據總長度1250s, Allan方差選擇矩形窗并將窗口長度設置為50s,窗口中點的步進長度16s,擬合方式選擇最小二乘擬合,具體如圖6、圖7所示。 由圖6、圖7可知,前300s的噪聲系數非常小,動態Allan方差分析圖也非常穩定,說明INS處于正常工作中狀態良好;而300s后圖像出現明顯的改變,相應傳感器的噪聲系數也出現了輕微的增加并在600s處出現了顯著的增加,說明受到振動環境的干擾傳感器的輸出特性發生了改變,而且由圖中可見出現了兩種不同分布的噪聲,這是由于振動臺進入開機的狀態后對INS有所干擾,隨后距離振動真正的開始大約有300s的時間間隔,無論在Allan方差分析圖或是在噪聲系數上都能夠清晰地反映出這幾種狀態的變化,完全符合實驗條件,也從側面佐證了殘差卡方檢驗配合動態Allan方差法在慣性傳感器故障檢測方面的有效性。 INS/GPS系統作為一種精密的測量系統,其內部傳感器極易受到外部溫度、濕度、振動、輻射等環境因素的影響及其本身器件老化造成的性能下降,而GPS的信號也容易受到干擾并不完全可靠,因此提出了綜合運用殘差卡方檢驗法和動態Allan方差法,分別從系統層面和傳感器層面對系統故障進行檢測及定位的方法。 其中,殘差卡方檢驗法借助Kalman濾波的中間變量構建評價方程,通過不斷的與閾值進行比較,可以實現實時地系統故障診斷,能夠從系統層面實時地對系統性能進行監測。當傳感器的性能下降或者外部信息出現故障時,能夠及時檢測出來并準確判斷故障發生的時間,為后續Allan方差的使用劃出范圍,大大優化了Allan方差的計算量。然而傳統的卡方檢驗法是建立在噪聲為Gauss分布的條件下對系統進行檢測,在實際工程應用中噪聲很難完全滿足理想的Gauss分布,因此判斷故障與否的閾值應根據實際情況適當調整。隨后的動態Allan方差法在已知故障發生時間的基礎上,彌補了殘差卡方檢驗法在出現故障位置識別方面的劣勢,但是由于該方法本身計算量較大且受計算方式的影響需要一定的數據長度來保證結果的準確性,因此實時性較差。 最后,借助這兩種方法的綜合使用,充分發揮各方法的優勢,可以在INS出現故障時及時準確地檢測出來,并準確定位至故障發生的位置,為INS故障后的修復提供依據,確保INS正常工作。 [1]Zhong M Y, Guo J, Guo D F, et al. An extended HiH∞optimization approach to fault detection of INS/GPS-integrated system[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(11) :2495-2504. [2]Pecht M, Dube M, Natishan M, et al. Evaluation of built-in test[J]. IEEE Transactions on Aerospace & Electronic Systems,2001, 37(1):266-271. [3]Vitanov I, Aouf N. Fault diagnosis for MEMS INS using unscented Kalman filter enhanced by Gaussian process adaptation[C]. 2014 NASA/ESA Conference on Adaptive Hardware and Systems(AHS), 2014:120-126. [4]Zhong M Y, Guo J, Yang Z H. On real time performance evaluation of the inertial sensors for INS/GPS integrated systems[J]. IEEE Sensors Journal, 2016, 16(17):6652-6661. [5]Evaluation[EB/OL].http://en.wikipedia. org/wiki/evaluation, 2015. [6]張娜, 李緒友. 動態Allan方差的理論改進及其應用研究[J].光學學報, 2011, 31(11):70-75. ZHANG Na,LI Xu-you. Research on theoretical improvement of dynamic Allan variance and itsapplication[J]. Acta Optica Sinica, 2011, 31(11):70-75. [7]翁浚, 成研, 秦永元,等. 車輛運動約束在SINS/OD 系統故障檢測中的應用[J].中國慣性技術學報, 2013, 21(3): 406-410. WENG Jun, CHENG Yan, QIN Yong-yuan, et al. Application of vehicle constraints in SINS/OD system's fault detection[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 406-410. [8]Hwang D H, Sang H O, Sang J L, et al. Design of a low-cost attitude determination GPS/INS integrated navigation system[J]. GPS Solutions, 2005, 9(4):294-311. [9]李冀辰, 高鳳岐, 王廣龍, 等. 光纖陀螺振動和變溫條件下的DAVAR分析[J].中國激光, 2013, 40(9):184-190. LI Ji-chen, GAO Feng-qi, WANG Guang-long, et al. Analysis of dynamic Allan variance for fiber optic gyro under vibration and variable temperature conditions[J]. Chinese Journal of Lasers, 2013, 40(9):184-190. [10]Galleani L. The dynamic Allan variance III: confidence and detection surfaces[J]. IEEE Transactions on Ultrasonics, Ferroelectric, and Frequency Control, 2011, 58(8): 1550-1558.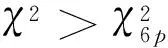
1.2 基于動態Allan方差法的傳感器故障檢測
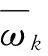
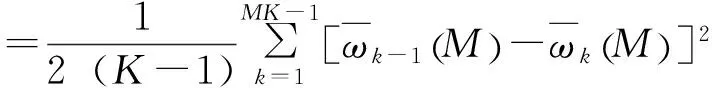

2 仿真驗證
3 實驗驗證
4 結論

