適用于矢量接收機的模糊自適應CKF方法研究

趙　琛，陳　帥，蔣長輝

(南京理工大學自動化學院，南京 210094)

0　引言

全球衛星導航系統作為一種十分重要的空間信息基礎設施，對于提升軍隊戰斗力和國防建設具有十分重要的意義[1]。但是一些惡劣的應用場景下，衛星導航的定位還存在一些問題[2]，比如在叢林密布的山區、高樓林立的市中心等，衛星信號被反射甚至被遮擋，這給衛星導航接收機的設計帶來了新的挑戰。

矢量跟蹤環路是由Spilker[3]首先提出，相對標量跟蹤而言，矢量接收機可以瞬間橋接被遮擋的信號和跟蹤信噪比更低的信號[4]。由于矢量跟蹤的優異性能，國內外學者進行了大量研究。矢量跟蹤相對標量跟蹤具有不需要重捕，同時能夠跟蹤更低載噪比信號的優勢[5]。矢量跟蹤在弱信號高動態下的性能，比標量跟蹤性能優異[6]。針對矢量跟蹤某一通道信號衰弱導致接收機誤差變大問題，文獻[7]討論了一種自適應Kalman濾波來克服這個問題。Lashley對標量跟蹤和矢量跟蹤性能進行了詳細的對比，得出矢量跟蹤在一定的動態下可以提高接收機跟蹤弱信號能力[8]，同時對不同矢量跟蹤中的不同鑒別器進行了比較[9],對跟蹤模型進行了分析和測試，但是沒有提到如何解決通道誤差傳播問題。

本文針對矢量跟蹤環路中部分通道衛星信號被遮擋導致的誤差在通道間傳播問題，為了避免對導航濾波器進行變維操作，給出了一種利用模糊控制[10]的自適應Kalman濾波算法。首先用一種標度因子來判決是否存在誤差通道，然后通過一個模糊控制器對Kalman濾波器增益進行調節，最后利用軟件接收機和衛星信號模擬器構建的仿真實驗平臺對算法進行了測試。

1　矢量跟蹤

1.1　矢量跟蹤環路

矢量跟蹤環的基本結構如圖1所示，由信號跟蹤、環路參數計算和導航濾波器3部分組成。矢量跟蹤環路改變了標量跟蹤環中跟蹤與導航解算相獨立的模式，將兩者結合起來，使用一個導航濾波器估計環路參數(包括載波頻率和碼相位)，通道之間共享了導航解算的結果，達到了通道之間的相互輔助。

1.2　導航濾波器

系統狀態方程為：

(1)

式中，Fk,k+1為狀態轉移矩陣，c為真空下光的速度，tb,k和tb,k-1分別為k時刻和k-1時刻的接收機鐘差，td,k和td,k-1分別為k時刻和k-1時刻的接收機鐘漂，δxk、δyk、δzk為地心地固坐標系下k時刻三軸位置誤差，δvx,k、δvy,k、δvz,k為k時刻地心地固坐標系三軸速度誤差，wk是系統噪聲，δxk-1、δyk-1、δzk-1為地心地固坐標系下k-1時刻三軸位置誤差，δvx,k-1、δvy,k-1、δvz,k-1為k-1時刻地心地固坐標系下三軸速度誤差。

系統觀測量選取各通道的碼相位測量值和載波頻率誤差測量值，觀測量與狀態量之間的關系如下：

(2)

zcode,k=hxδxk+hyδyk+hzδzk+c·tb,k+wcode,k

zcarr,k=hxδvx,k+hyδvy,k+hzδvz,k+c·td,k+wcarr,k

(3)

式中，wcode和wcarr分別為碼相位跟蹤誤差噪聲和載波頻率跟蹤誤差噪聲。

hx、hy、hz分別為單位觀測矢量的X軸、Y軸、Z軸分量，有：

(4)

(5)

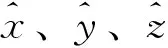
1.3　自適應導航濾波器

矢量跟蹤導航濾波器采用Kalman濾波，Kalman濾波器的性能將影響整個環路的跟蹤性能。

考慮線性離散系統，有：

(6)

其中，xk為k時刻的狀態向量，Φk,k-1為狀態轉移矩陣，zk為量測向量，Hk為量測矩陣，wk-1和vk分別為系統噪聲和量測噪聲，并且滿足：

式中，Qk≥0為系統噪聲方差陣,Rk>0為量測噪聲方差陣。

(7)

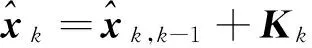
(8)

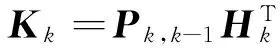
(9)

(10)

Pk=(I-KkHk)Pk,k-1

(11)

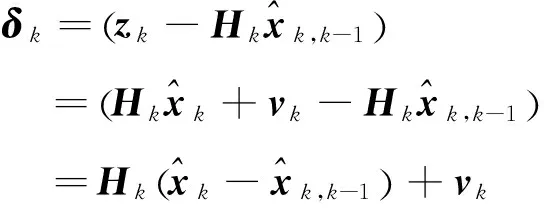
(12)

新息方差計算公式如下：

(13)

新息方差的理論定義為：

(14)

標度因子為：

(15)

當標度因子大于設定閾值時，就認為存在跟蹤通道影響跟蹤環路結果。濾波正常的情況下，標度因子的值在1附近。然后具體對每個通道進行分析。

Λk=trace(Εk>Ωk)

(16)

式(16)計算結果是一個對角矩陣，通過矩陣上的值可以推斷哪個通道存在問題。式(9)可以寫成如下形式：

(17)

根據式(17)可知，當第j通道量測出現連續野值時，如果將相應的R(j,j)放大，可以調節狀態更新時誤差通道對應的增益值，消除誤差通道影響。這里乘以一個參數，需要根據量測的不正常程度來決定。通過Ε和Ω對角線上的對應元素的比值來決定，這里采用模糊控制算法描述這種關系。

定義矩陣β為：

βk(i,i)=Ek(i,i)/Ωk(i,i)

(18)

濾波正常的時候βk(i,i)的值在1附近。

2　模糊控制器

模糊控制的輸入是βk(i,i)，輸出是Λk(i,i)。輸入有3個模糊集：S=小，N=正常，B=大。輸出有3個模糊集：S=小，N=正常，B=大。具體如圖2、圖3所示。

模糊控制的輸出對R陣進行自適應，Kalman濾波的基本公式同式(7)、式(8)、式(10)和式(11)，含有R陣的濾波增益公式如式(19)所示。

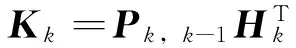
(19)

3　仿真試驗

3.1　仿真平臺

仿真實驗平臺主要由基于Matlab的矢量跟蹤軟件接收機、衛星信號模擬器、中頻信號采集器和電腦4部分組成，詳細流程如圖4所示。整個操作流程如下：首先通過軌跡發生器產生相應的軌跡文本文件，然后將文本文件注入衛星信號模擬器的控制端，控制端控制衛星信號模擬器產生相應設置場景的衛星信號，同時衛星信號經過天線傳給和天線相連接的中頻信號采集器，中頻信號采集器采集衛星信號并存儲下來供軟件接收機使用。這里采用的中頻信號采集器的采樣率為16.369MHz，中頻信號頻率為3.996MHz。

3.2　仿真實驗

軌跡設置如下：起點為北緯31.1341°、東經118.9740°、高程57447.0m，終點為北緯33.4905°、東經118.9740°、高程54582.0m，速度恒定為1000m/s，仿真時間40s，參與導航的衛星號為03、07、08、11、17、19、20和24。其中，03號和07號衛星信號通過模擬器設置一段時間被遮擋，然后又恢復正常，具體的可見性如圖5所示。07號衛星在第20s～30s被遮擋，03號衛星在26s～34s被遮擋，剩余的衛星在整個過程中保持正常。

圖6～圖8展示了部分衛星信號被遮擋的場景下，地心地固坐標系下接收機定位誤差的對比。常規的矢量跟蹤環路在部分衛星信號被遮擋的情況下，3個軸的定位誤差明顯變大，自適應跟蹤環路3個軸的定位誤差明顯更小，并且和正常情況相比，定位誤差差異不大，這說明了算法的有效性。

4　結論

本文介紹了一種利用模糊控制的自適應矢量跟蹤環路用來處理矢量接收機在部分衛星信號被遮擋環境下的通道誤差傳播問題，避免了對導航濾波器的變維操作，提高了矢量跟蹤的穩定性，通過調整相應通道的量測方差來改變增益，從而消除誤通道誤差的傳播。最后,通過基于矢量跟蹤的軟件接收機進行仿真驗證，證明了該方法能夠很好地抑制誤通道誤差傳播，提高矢量接收機穩定性。

[1]謝鋼. GPS原理與接收機設計[M].北京:電子工業出版社, 2009.

XIE Gang. Principles of GPS and receiver design [M].Beijing: Electronics Industry Press, 2009.

[2]劉建業,曾慶化,趙偉,等.導航系統理論與應用[M].西安:西北工業大學出版社, 2010.

LIU Jian-ye, ZENG Qing-hua, ZHAO Wei, et al. The theory and application of navigation system [M]. Xi’an:Northwestern Polytechnical University Press, 2010.

[3]Parkinson B W, Spilker J J, Axelrad P, et al. Global positioningsystem: theory and applications[M]. Washington DC: American Institute of Aeronautics and Astronau-tics, 1996.

[4]程俊仁, 劉光斌,姚志成，等. 一種魯棒GNSS矢量跟蹤環[J]. 航空學報, 2014,35(11):3106-3114.

CHENG Jun-ren, LIU Guang-bin, YAO Zhi-cheng, et al. A robust GNSS vector tracking loop[J]. Journal of Aeronautical Engineering, 2014,35(11):3106-3114.

[5]Li Q, Wang W, Guo X, et al. A design and performance analysis of vector-based tracking loop receiver[C]. IEEE International Conference on Signal Processing, 2012, 3:2231-2235.

[6]Liu J, Cui X W, Lu M Q, et al. Vector tracking loops in GNSS receivers for dynamic weak signals[J]. Journal of Systems Engineering and Electrics, 2013,24(3):349-364.

[7]趙思浩, 陸明泉, 馮振明. 基于自適應濾波的GNSS矢量鎖定環路[J]. 哈爾濱工業大學學報, 2012,44(7):139-143.

ZHAO Si-hao, LU Ming-quan, FENG Zhen-ming. GNSS vector locking loop based on adaptive filtering[J]. Journal of Harbin Institute of Technology, 2012,44(7): 139-143.

[8]Lashley M, Bevly D M. Analysis of discriminators based vector tracking algorithms[C]. Proceedings of 2007 ION NTM, 2007:570-576.

[9]Lashley M. Modeling and performance analysis of GPS vector tracking algorithms[D]. Auburn University, 2009.

[10]張池平, 劉宗堯.一種改進的自適應模糊Kalman濾波算法[J].計算機工程與應用,2007, 43(28): 25-28.

ZHANG Chi-ping, LIU Zong-yao. An improved adaptive fuzzy Kalman filtering algorithm[J]. Computer Engineeringand Applications, 2007, 43(28):25-28.