考慮繞行效應的人員疏散元胞自動機模型研究*

胥　旋,史聰靈,李　建,車洪磊

(中國安全生產科學研究院 地鐵火災及客流疏運安全北京市重點實驗室，北京 100012)

0　引言

近年來，疏散研究一直是公共安全領域的熱點問題之一。研究人員提出大量的疏散模型用于模擬人群的疏散過程，這些模型整體上可分為離散模型[1-2]和社會力模型[3]。元胞自動機作為離散模型的代表，由于其簡單的規則和快速的計算效率，是應用最為廣泛的方法模型之一，在用于疏散的經典元胞自動機模型的基礎上，研究者們提出了各類擴展模型。Kirchner等[4-5]提出一種場域模型，將遠距離空間相互作用轉化為有吸引力的局部相互作用。Yuan等[6]模擬一個有多個出口的房間疏散，在其擴展的CA模型中考慮了人類行為，包括：慣性效應、群體效應和非冒險效應；Yue等[7]通過引入4個動態參數：方向參數、空參數、前向參數和類別參數，描述行人對周圍環境的判斷，從而實現行人流的模擬；毛占利等[8]建立了疏散路徑受阻情況下的人員疏散模型；陳長坤等[9]建立了行李攜帶人員疏散元胞自動機模型。大部分的元胞自動機疏散模型一般認為，行人在每1個時間步中選擇1個未被占用的元胞或保持靜止不動，其所選擇的方向是基于與相鄰元胞的占用條件有關的概率。一般來說，表示目標吸引力的擇優方向或自驅動方向的概率最大，當這個方向不可到達時，它的轉換概率值將轉移到其他方向，如果可能的話，行人將選擇另一個方向來避開障礙物。然而，概率轉移的簡單處理忽略了行人對障礙物的主動響應，這在模擬過程中可能出現不真實的現象。在模型中，對行人的運動行為考慮的越細致，模擬越接近于真實現象[10-15]。因此，本文旨在研究行人被堵塞時的繞行行為，并建立考慮繞行行為的元胞自動機模型(DCA)，模型設置一個靈活的規則，使行人受阻時能夠合理地繞過前面的障礙物，通過建立一個疏散場景，利用DCA模型分析瓶頸處的成拱現象，并將結果與文獻[1]中的無后退的隨機行走模型和文獻[4]中的場域模型進行比較。

1　考慮繞行的元胞自動機模型(DCA模型)

經典離散模型認為，行人可選擇的有上、下、左、右4個方向，4個方向的移動概率值總和為1，其中面向出口方向的移動概率最大；在每個時間步，行人會根據4個方向上元胞的占有情況，調整各個方向的移動概率，但4個方向上的移動概率總和始終為1，除非4個方向全部堵住。本文提出的DCA模型是文獻[1]中經典離散模型的改進模型，改進點主要包括：

1)DCA模型認為當行人前方有空元胞可以占據時，直接將后退概率設為0。這是為了避免模型中出現人員在密集人群中不合理的后退運動。

2)DCA模型認為如果前進方向沒有空元胞，同時后退方向有空元胞時，行人可能會原地不動，而并非像經典離散模型中行人會選擇后退。

3)DCA模型提出等位線的概念，并建立繞行規則。等位線是由與出口距離相等的元胞組成的，當行人2個前進方向都被堵塞時，如果感知區域等位線上有空元胞，行人可以先后退，然后在下1個時間步繞行到達等位線上的元胞；如果感知區域等位線上沒有空元胞，行人將保持靜止(即使后退方向有空元胞)。感知區域是指行人在這個區域內尋找等距的且未被占用的元胞。

如圖1所示，×表示2個前進方向被阻擋，此時行人有3種選擇：靜止、向+y方向運動、向-x方向運動。其中，+y和-x方向由于背離出口，稱之為后退方向。如果右上方正方形所示的等位線(虛線)有空元胞，其可以先后退到+y方向，然后再向+x方向運動以繞過障礙；如果左下方正方形所示的等位線(虛線)有空元胞，其可以先后退到-x方向，然后再向-y方向運動以繞開障礙。邊長為r的正方形區域代表了行人的感知范圍，是一個不可見的但可以搜索的范圍。

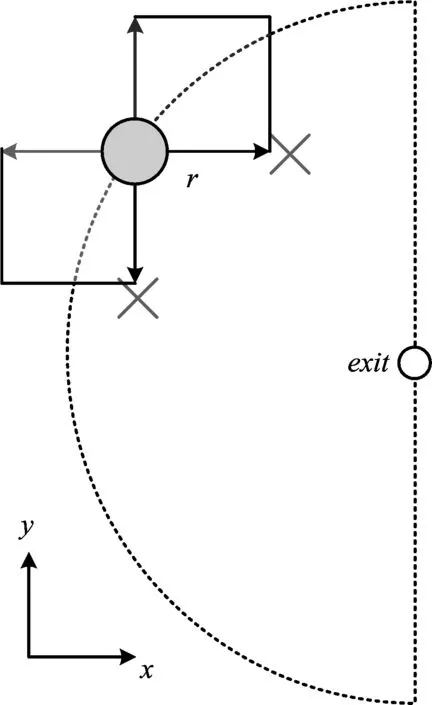
圖1　繞行行為圖解Fig.1　Illustration of detour behavior

2　模擬及結果分析

為檢驗模型的模擬效果，根據文獻[1]的描述構建1個16 m×16 m的大廳疏散場景，每個行人占據0.4 m×0.4 m的空間，默認狀態下前進運動的概率為0.8。

2.1　疏散過程

如圖2所示，疏散發展過程可分為3個階段：

1)聚集階段。大廳中的行人開始靠近出口運動，人群變得越來越密集。由于上層行人偏向右下運動，下層行人偏向向右上運動，人群外沿呈拋物線形狀，如圖2(a)所示。

2)調整階段。隨著越來越多的行人被前面的行人阻擋，他們開始按照繞行規則調整自己的位置，處于拋物線頂點的行人開始橫向運動以到達靠近出口的位置，如圖2(b)所示。

3)穩定階段。當行人找到最佳位置后，他們中的大多數人會保持靜止，在等位線上下的波動很小。因此，所有的行人保持離出口最近的距離，人群保持拱形。隨著行人離開大廳，半圓的半徑逐漸減小，如圖2(c)和(d)。

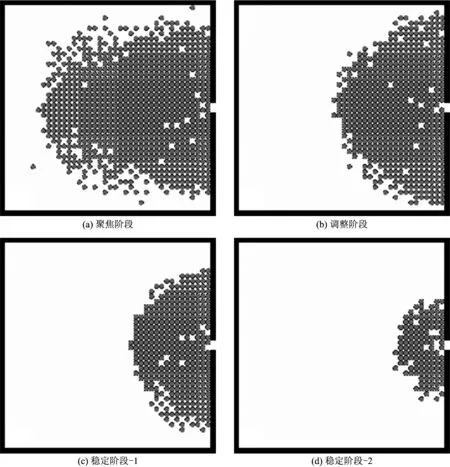
圖2　疏散過程Fig.2　Evacuation process

2.2　繞行對疏散過程成拱的影響

為定量研究繞行行為對成拱過程的影響，引入2個變量：最大距離(Maximum Distance,MD)和調整速度(Regulation Speed,RS)，來描述疏散過程中的成拱行為。最大距離定義為行人到出口的最大距離(歐式距離)，調整速度是最大距離減少的速率。行人的感知范圍決定了繞行的可能性，因此研究感知范圍對這2個變量之間的影響作用，以闡明繞行行為對成拱的影響。

為了方便起見，把出口寬度設為零，即沒有人可以離開大廳，這樣更容易觀察拱的形成過程。圖3給出了最大距離隨感知范圍的變化情況。從圖3中可以看出，MD的變化可以分為3個階段，分別對應于2.1節中疏散過程的3個階段。在第I階段中，MD的值急劇下降，表明在疏散開始時，人群迅速向出口運動；在第II階段，MD的下降速度減慢，表明人群在逐漸調整，以尋找離出口最近的位置；在第III階段，由于出口是不可通過的，MD將保持一個恒定值，表明行人找到了最佳位置后，大多數人都會保持靜止不動。

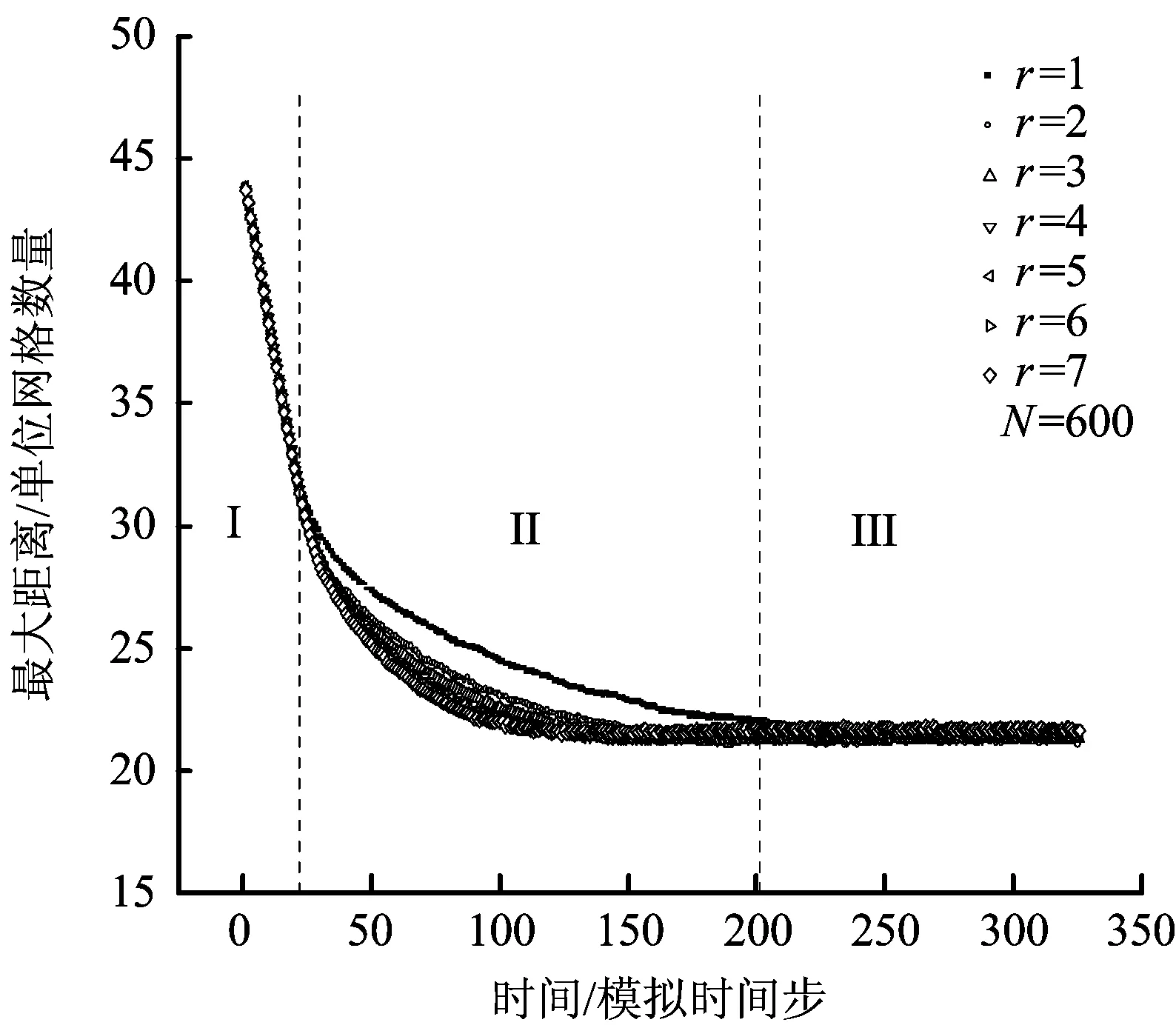
圖3　最大距離隨感知范圍的變化情況Fig.3　Change of maximum distance with perceptual range for W=0

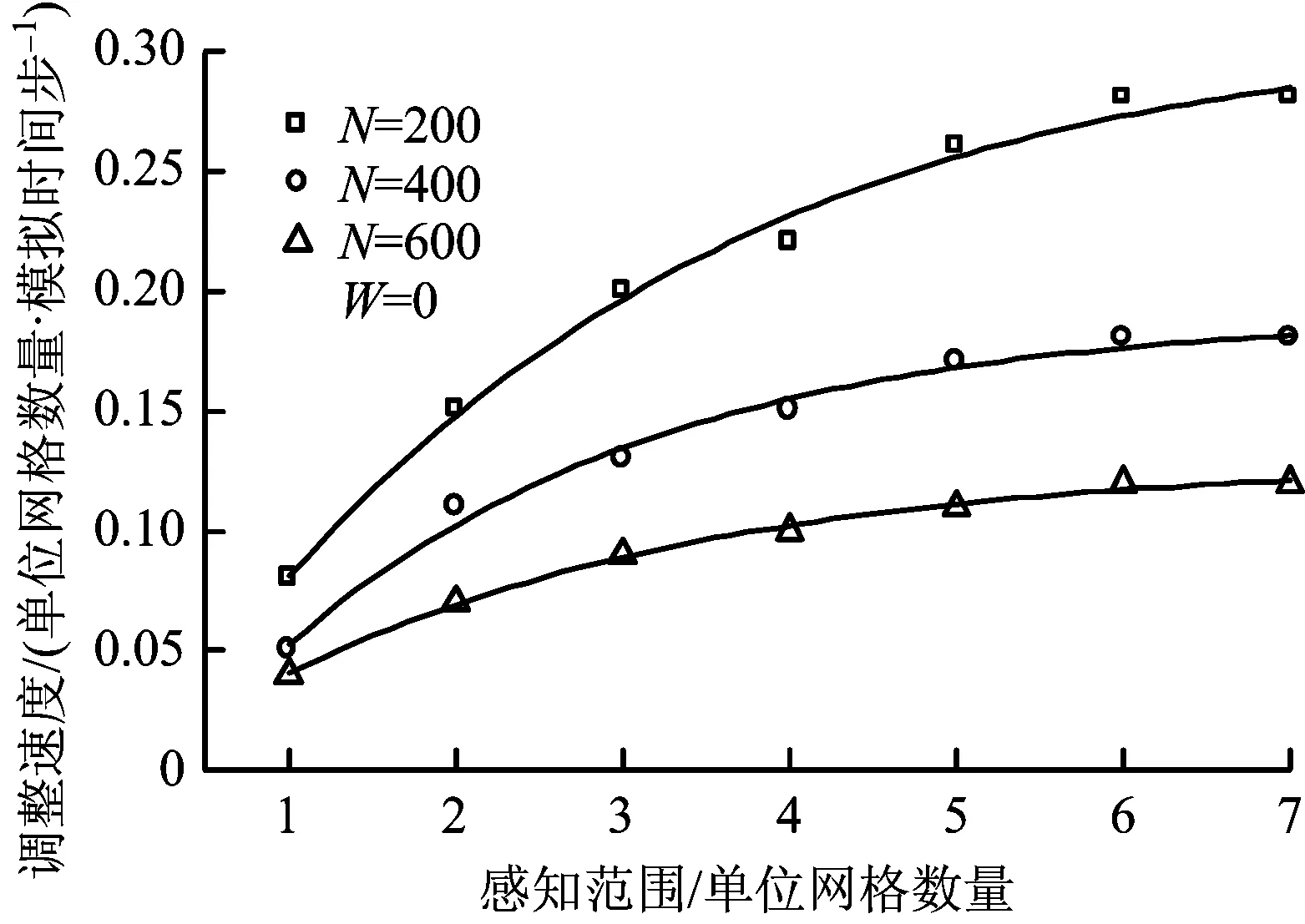
圖4　調整速度隨感知范圍的變化情況Fig.4　Regulation speed as a function of perceptual range for W=0

從圖3中可以看出，在聚集階段(第I階段)，不同的感知范圍下，MD曲線沒有顯著差異；進入第II階段后，被堵塞的行人開始調整位置，使自己更接近出口，人群從拋物線模式轉換成弧形模式。本文將MD的平均減小速率ΔMD/Δt定義為調整速度RS。圖4給出了不同數量行人下，RS與感知范圍之間的關系。結果表明，RS的值隨著感知范圍的增大而增大。一個較大的感知范圍意味著，行人在他的搜索區域中有更大的機會找到空的元胞。因此，在較大的感知范圍內，繞行趨勢越強，弧形形成越快。當感知范圍足夠大，足以讓行人繞行時，RS的值就不會隨著感知范圍的增加而明顯增加。

3　模型比較

文獻[1]中的無后退有偏隨機走動模型和文獻[4]中的場域模型是疏散領域的2種經典元胞自動機模型，本文將所構建的DCA模型與上述2類模型進行比較。疏散情景設置如下：大廳內初始行人隨機分布600人，出口寬度0.8 m；在DCA模型中，感知范圍設為5；場域模型中不考慮動態場(kD= 0)，靜態場的敏感性參數kS= 10；行人之間的沖突解決方法詳見文獻[2]；為描述方便，文獻[1]中的模型簡稱為模型A，文獻[4]中的模型簡稱為模型B。

3.1　與模型A的比較

模型A中，模擬過程中的人群分布如圖5所示。在該模型中，-x方向被定義為行人在任何情況下都不會行走的后退方向。當前進方向被阻擋時，行人盡可能向上或向下運動，如中心受阻的行人會不斷向上或下移動，會逐漸遠離出口(這種行為其實是不合理的)。因此，在穩定階段，人群呈現矩形分布。在DCA模型中，+y方向也被定義為上方行人的后退方向，-y方向為下方行人的后退方向。當前進方向被阻擋時，除非在等位線上有空元胞，否則其不會選擇遠離出口運動。因此，DCA模型避免了不合理的向后運動，人群呈現出一種弧形模式。

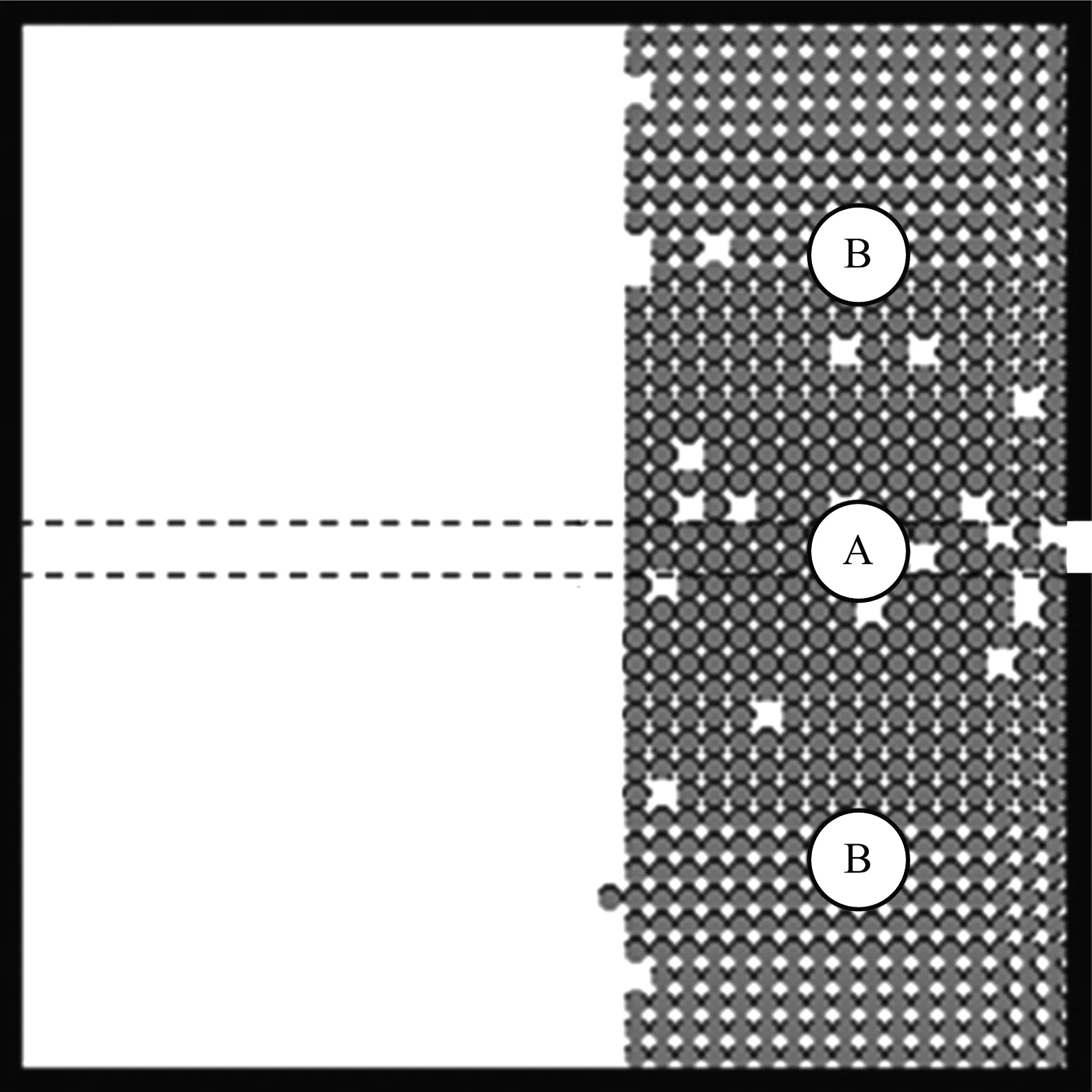
圖5　無后退的有偏隨機走動模型(模型A)中人群分布Fig.5　A rectangular distribution of crowd in the evacuation simulation with bias-random walk model without back step(Model A).

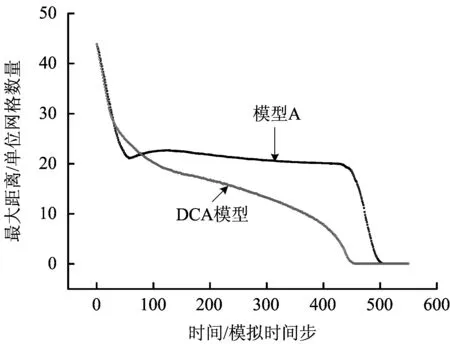
圖6　模型A和DCA模型的最大距離隨時間的變化情況 Fig.6　Maximum distance against time for Model A and DCA model

圖6展示了模型A和DCA模型中，MD值隨疏散時間的變化情況。模型A中，MD值在聚集階段后略有增加，這意味著被阻擋的行人被迫側向運動，此后人群保持矩形分布，MD值隨著人群逐漸離開大廳而緩慢降低，在最后階段，隨著所剩無幾的行人離開大廳，MD的值迅速下降；而DCA模型由于人群在第II階段始終保持弧形分布，因此MD值呈現平穩的逐漸下降趨勢。

圖7展示了模型A和DCA模型中，疏散人數隨時間的變化情況。2類模型中，在疏散早期和中期階段，疏散人數呈線性增加。恒定斜率值意味著出口呈現穩定和飽和的流出。但是，在后期階段，對于模型A，疏散曲線的斜率變小，即出口的效率降低，這是B區域(圖5)的行人需要一定的時間到達出口造成的，由于該模型中，行人運動方向的選擇是基于概率的，所以在某些時間步可能偏離出口。據觀察，這個區域的行人在靠近出口時，會來回運動。當出口前面的行人已經疏散出去時，其可能沒有順序跟上。因此，在疏散的最后階段，沒有足夠的行人來維持出口的飽和流量。對于DCA模型，B區域的行人在接近出口時不能向后運動，其會緊跟前方的行人，在出口前總有足夠的行人。所以，不管是在疏散前中期還是在后期，出口的流量始終處于飽和狀態，曲線的斜率基本不變。

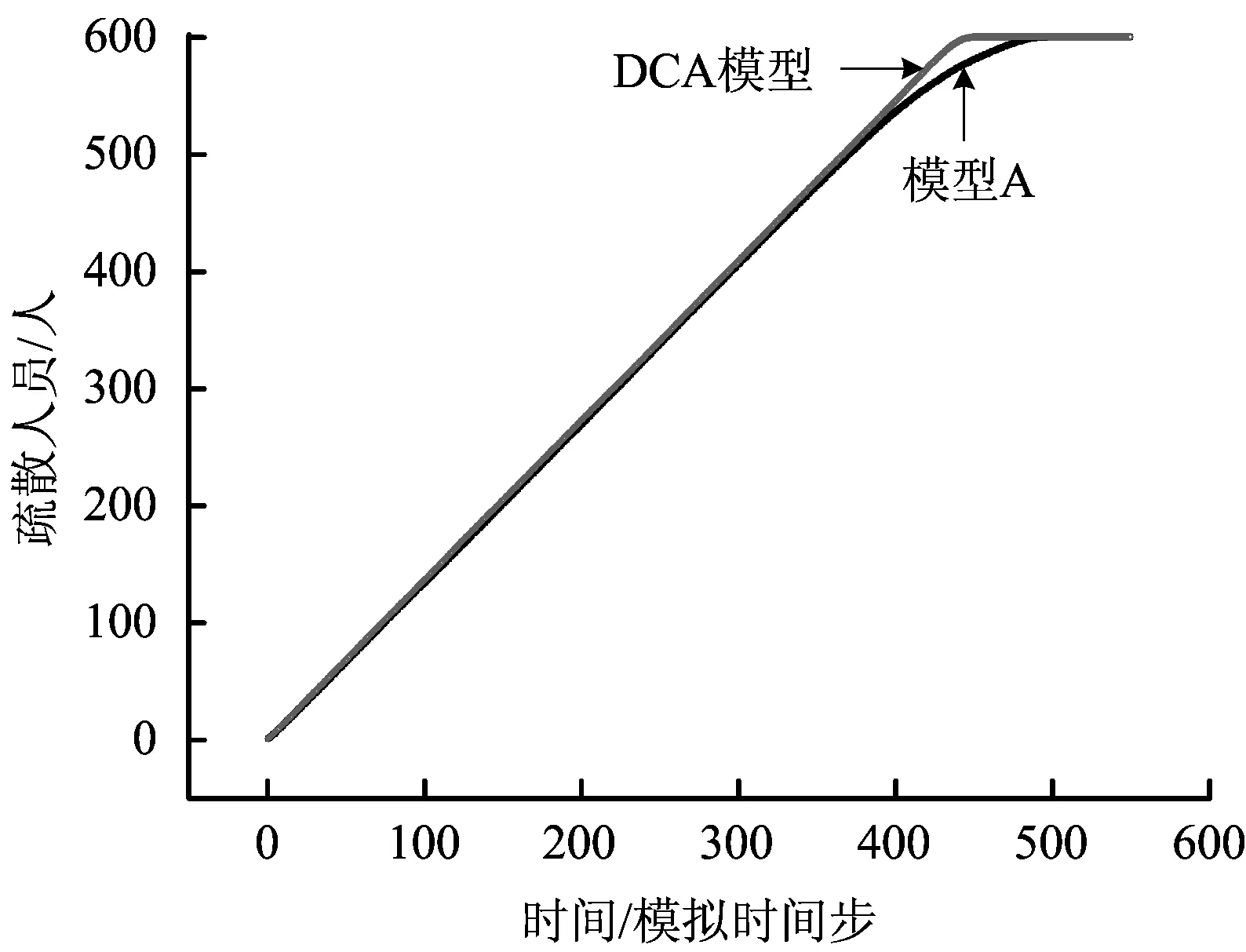
圖7　模型A和DCA模型中疏散人數隨時間的變化情況Fig.7　The number of evacuated pedestrians as a function of time for Model A and DCA model

3.2　與模型B的比較

DCA模型和模型B在行人的分布方面沒有太大的區別，均呈現拱形分布，但在細節方面有所不同。圖8展示了模型B和DCA模型中，MD值隨疏散時間的變化情況。結果發現，在疏散中期，即行人調整位置的時期，模型B的MD值明顯高于DCA模型。這是由于模型B的規則中設定了除非4個方向均受阻，否則行人必須走1步，即使這使其遠離目標。模擬發現，在擁擠狀態時，行人經常擺動，因此MD值較DCA模型偏大。這種擺動與日常經驗不符，經驗表明，人群中焦慮的人希望繞過前面的人到達目的地，但如果其發現沒有比當前位置更近的空間，其會保持靜止，而不會不停地跑來跑去。DCA模型解決了模型B中的這一不合理規則，當行人受阻時，只有當他能夠繞行進入等位線的空元胞時才能后退，否則，其將保持靜止。因此，DCA模型減少了行人流中這種不合理的后退行為。

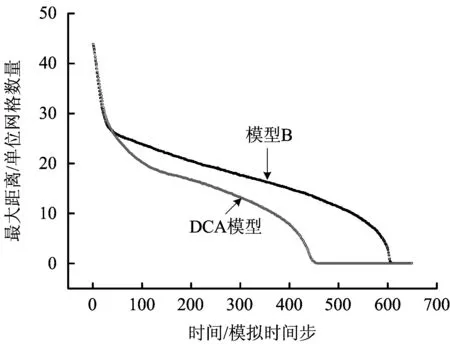
圖8　模型B和DCA模型中最大距離隨時間的變化情況Fig.8　Maximum distance against time for Model B and DCA model

圖9展示了2種模型中行人后退運動的比例情況，即某一時刻后退運動的行人占留在大廳的人數比。從圖9中可以明顯看出，模型B的后退運動行為比DCA模型更為頻繁。

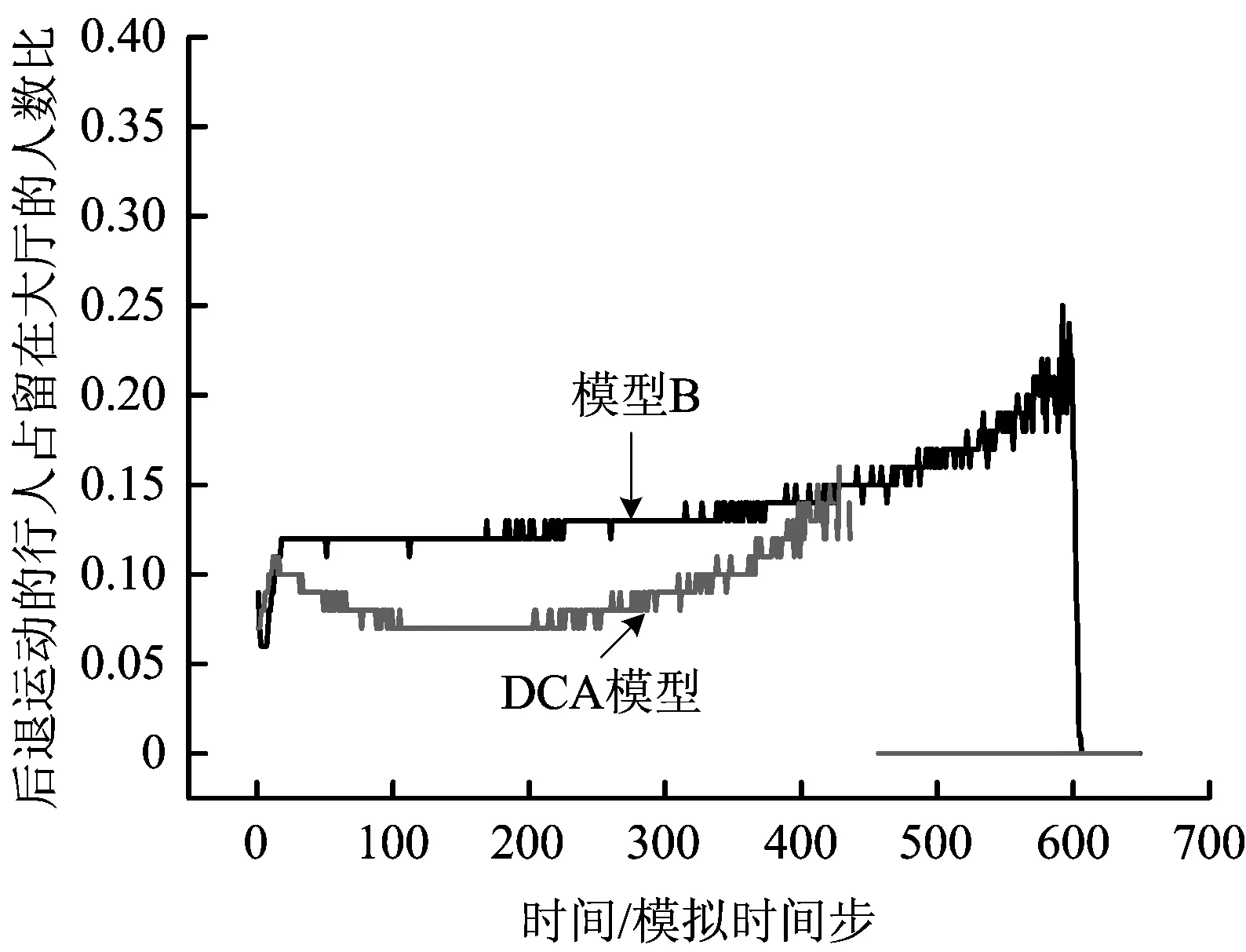
圖9　模型B和DCA模型中后退運動比例隨時間的變化情況Fig.9　Ratio of backward movement with time for Model B and DCA model

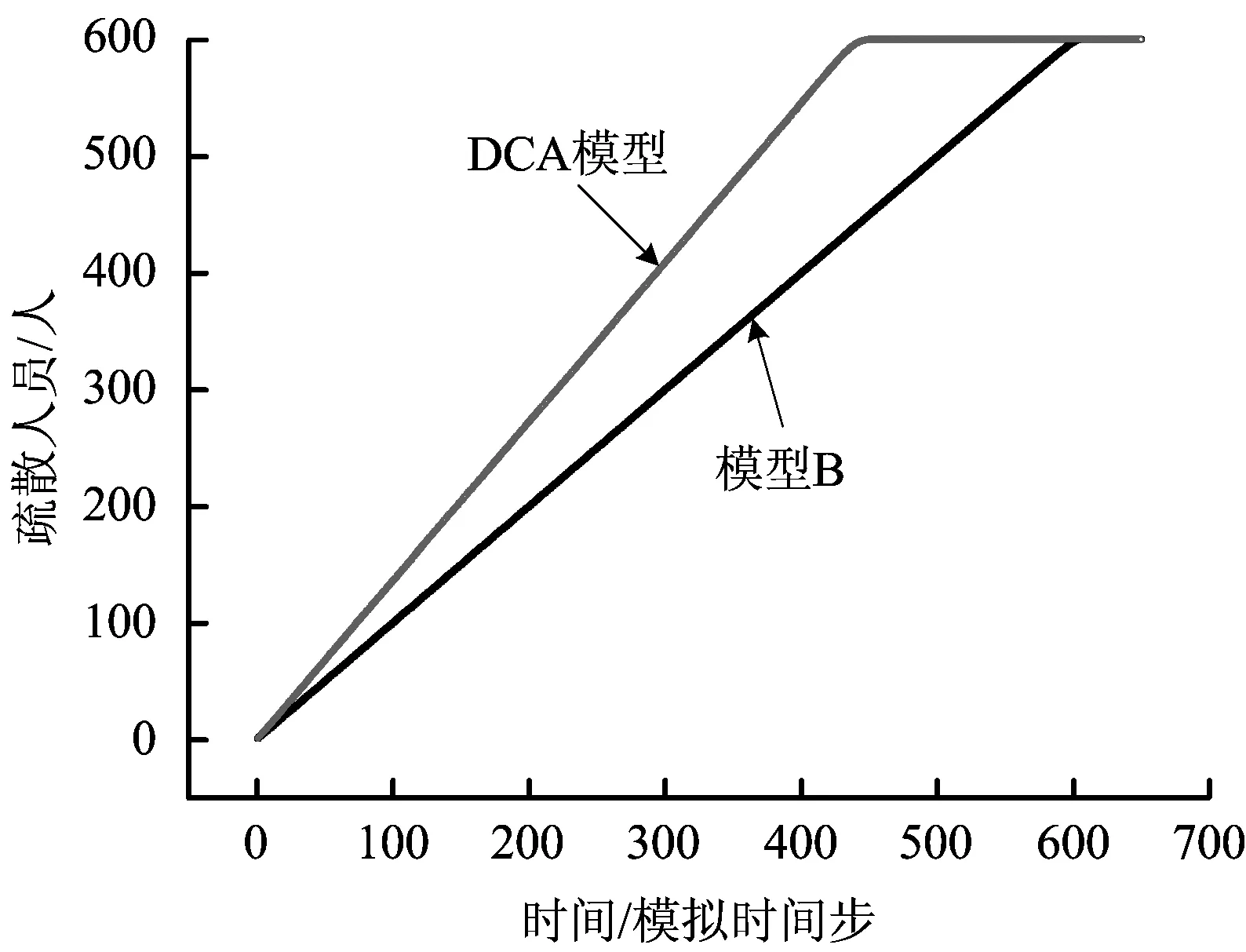
圖10　模型B和DCA模型中疏散人數隨時間的變化情況Fig.10　The number of evacuated pedestrians as a function of time for Model B and DCA model

圖10展示了模型B和DCA模型中，疏散人數隨疏散時間的變化情況。結果表明，2種模型的人員流出率都保持不變，但模型B的值比DCA模型的值小。這是因為模型B采用并行更新規則，而DCA模型采用隨機順序更新規則。模型B需要花費更多的時間步來解決與行人間的沖突。

4　結論

1)提出一個考慮繞行行為的元胞自動機模型(DCA模型)，模型所建立的繞行規則規定了被阻擋的行人是繞過障礙物還是保持靜止不動。與繞行行為密切相關的感知范圍參數決定了繞行傾向，該參數值越大，行人繞行傾向就越強。

2)根據人群的分布情況，疏散過程大致分為3個階段：聚集階段、調整階段和穩定階段。在調整階段，繞行行為使被阻擋的行人能夠繞過障礙物，從而在出口前形成拱形現象。感知范圍越大，拱形形成的越快，人群分布可快速進入穩定階段。

3)DCA模型與無后退的有偏隨機走動模型和場域模型的模擬結果表明，DCA模型解決了前種模型中人群呈現矩形分布的不合理現象，同時解決2種模型中人員在密集人群中不合理后退行為。因此，DCA模型的后退運動更具目的性和合理性，仿真結果也更為合理。DCA模型進一步發展了元胞自動機模型，并可與其他元胞自動機模型方法結合，用于行人動力學研究。

[1]TAJIMA Y, NAGATANI T. Scaling behavior of crowd flow outside a hall[J]. Physica A Statistical Mechanics & Its Applications, 2001, 292(1):545-554.

[2]BURSTEDDE C, KLAUCK K, SCHADSCHNEIDER A, et al. Simulation of pedestrian dynamics using a two-dimensional cellular automaton[J]. Physica A Statistical Mechanics & Its Applications, 2001, 295(3):507-525.

[3]HELBING D, FARKAS I, VICSEK T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(6803):487.

[4]KIRCHNER A, SCHADSCHNEIDER A. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics[J]. Physica A Statistical Mechanics & Its Applications, 2002, 312(1):260-276.

[5]KIRCHNER A, KLUEPFEL H, NISHINARI K, et al. Discretisation effects and the influence of walking speed in cellular automata models for pedestrian dynamics[J]. Journal of Statistical Mechanics Theory & Experiment, 2004(10):P10011.

[6]YUAN W, TAN K H. An evacuation model using cellular automata[J]. Physica A Statistical Mechanics & Its Applications, 2007, 384(2):549-566.

[7]YUE H, HAO H, CHEN X, et al. Simulation of pedestrian flow on square lattice based on cellular automata model[J]. Physica A Statistical Mechanics & Its Applications, 2007, 384(2):567-588.

[8]毛占利, 劉暢. 疏散路徑受阻情況下的人員疏散模型及算法[J]. 安全與環境學報, 2017(5):1873-1878.

MAO Zhanli,LIU Chang.Evacuation model and the algorithm on the condition of the urgent obstructed evacuation route[J].Journal of Safety and Environment,2017(5):1873-1878.

[9]陳長坤, 王楠楠, 席冰花. 行李攜帶人員疏散元胞自動機模型研究[J]. 中國安全科學學報, 2014, 24(7):3-9.

CHEN Changkun,WANG Nannan,XI Binghua.Research on evacuation cellular automata model of evacuees with luggage[J].China Safety Science Journal,2014,24(7):3-9.

[10]苗志宏, 李智慧. 一種基于SPH方法的人員疏散混合模型及模擬[J]. 自動化學報, 2014, 40(5):935-941.

MIAO Zhihong,LI Zhihui. A hybird evacuation model and simulation based on SPH method[J]. Acta Automatica Sinica,2014,40(5):935-941.

[11]王桂芬, 張憲立, 閻衛東. 建筑物火災中人員行為EXODUS模擬的研究[J]. 中國安全生產科學技術, 2011, 7(8):67-72.

WANG Guifen,ZHANG Xianli,YAN Weidong.Building fire behavior modeling of EXODUS[J].Journal of Safety Science and Technology,2011,7(8):67-72.

[12]劉夢婷, 蔣美英. 考慮人群擁堵的疏散出口選擇行為研究及建模[J]. 中國安全生產科學技術, 2016, 12(9):157-163.

LIU Mengting,JIANG Meiying.Study on exit choice behavior in evacuation considering crowd congestion and its modeling[J].Journal of Safety Science and Technology,2016,12(9):157-163.

[13]張立紅, 王策源, 楊光,等. 基于行人疏散模型的建筑出口設計優化研究[J]. 中國安全生產科學技術, 2014(10):100-105.

ZHANG Lihong,WANG Ceyuan,YANG Guang,et al.Study on optimization of building exits design based on pedestrian evacuation model[J].Journal of Safety Science and Technology,2014(10):100-105.

[14]陳海濤, 劉占, 靳紅雨,等. 雙出口疏散吸引區域模型建立與模擬分析[J]. 中國安全生產科學技術, 2017, 13(7):55-61.

CHEN Haitao,LIU Zhan,JIN Hongyu,et al.Modeling and simulation analysis on evacuation attraction region model for double exits[J].Journal of Safety Science and Technology,2017,13(7):55-61.

[15]呂春杉, 翁文國, 楊銳,等. 基于運動模式和元胞自動機的火災環境下人員疏散模型[J]. 清華大學學報(自然科學版), 2007, 47(12):2163-2167.

LYU Chunshan， WENG Wenguo， YANG Rui， et al.Fire evacuation model based on motor schema and cellular automaton[J].J Tsinghua Univ ( Sci & Tech),2007,47(12):2163-2167.