對不動點定理的介紹以及對高中解題構造數列方法的研究

寧波市效實中學 浙江寧波 315000

不動點理論在數學方程中有著廣泛的應用，諸如函數方程、微分方程、代數方程等[1]。我們在解答高中數學的數列問題時，就會經常會應用到不動點方程的f(x)=x[2]。不動點理論是研究不動點有無數個性質與求法，因此我們要在構造數列的過程中靈活地應用不動點定理。

1 不動點定理的介紹及選題

1.1 不動點概念

不動點原理又被稱為巴拿赫（Banach）不動點原理。簡單來講，就是一個數學函數的定義域中包含該函數的值域，也就是說對于f(x)=x這個方程始終會有一個根存在。因此不動點原理的本質其實就是零點存在性定理。

1.2 選題背景

數學函數中的"不動點"理論雖然是中學教材里的選修內容，但老師也會重點講解這方面的知識，因為很多同學在這里都會遇到學習上的問題，不能夠解答，如果能夠熟練掌握，合理地利用”不動點”理論，就會使大家更加容易的解決一些復雜、難以搞定的數學問題。所以近年來“不動點”理論在高中數學中得到了廣泛的應用。許多同學也是因為掌握了不動點定理來解決數學問題的方法，從而提高了自己的數學成績。

1.3 選題意義

根據遞推公式來求解數列通項公式、數列的單調性、有界性以及收斂性，這些性質和題型是高考中的熱點。其中有一些根據遞推公式很難求出通項公式的數列，解決這種數列問題時經常要從函數的性質來出發。在一些高水平的競賽題中，經常會出現這種綜合的數列問題。不僅在競賽題中，近幾年高考題目也有向該題型的方向轉化的趨勢。因此，該定理的應用還是極為廣泛的。

1.4 研究內容

①將不動點原理的迭代思想運用到數列的遞推關系中，進而解決通過遞推關系難求數列通項公式的問題。

②利用不動點原理的迭代思想，給出對一些數列的有界性性質的證明。

③通過不動點原理，研究數列的單調收斂性質，研究過程中還會運用到特征函數的一些性質，解決高考中的相關題目。

2 不動點定理在數列中的應用

2.1 迭代函數、迭代思想的應用

迭代函數是不斷的與自身復合的函數，這個過程叫做迭代[3]。

例：fn+1(x)=f(fn(x))

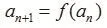
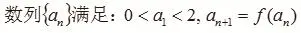
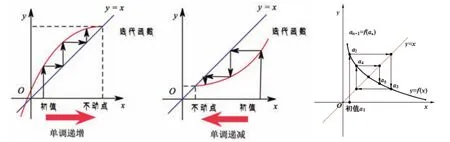
2.2 不動點裂項

對于一階遞推式an+1=f(an)，若f(x)為多項式函數（或分式多項式函數），且α為f(x)的不動點，那么f(an)-α一定有因式 an-α,設 f(an)-α=(an-α)·A

這種改寫遞推式為裂項形式的方法稱為不動點裂項。不動點裂項是改造遞推式從而嘗試求通項的重要方法，也是得到數列裂項放縮的重要手段。

下面舉例幾種常見類型的構造形式：

（1）數列單調性、數列放縮綜合應用。在數列的綜合應用中，我們往往可通過對不動點及迭代函數圖像的分析，構造出符合題目結論需要的形式，從而轉化為求不等式放縮或求函數最值問題，不動點可謂給構造提供了理論依據，有效避免了盲目變形瞎湊的做法[4]。

幾種常見的應用舉例：

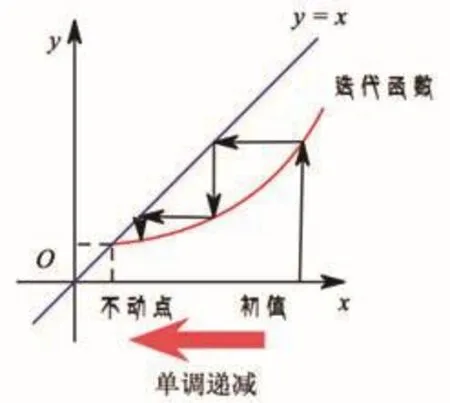
分析：求范圍問題通常可用數學歸納法，本文將另一個角度來闡述數列的有界性問題。

根據前文描述，我們可以通過迭代函數圖像，并觀察an變化規律，符合（1）中結論。

下面通過不動點的構造，我們來證明：

題目顯然與不動點有關，首先，利用絕對值不等式對式子進行變形：

3 結語

通過對不動點的學習，在解答高中數列問題時，可以利用其圖像對題目所求內容進行對比，進而利用不動點進行構造，最后通過等比、等差放縮或進行裂項，取倒數、取對數等手法進行求證。只要掌握了不動點，就是掌握了考試的一大利器。