一種基于核PCA的網絡流量異常檢測算法

曾 建 華

(上饒師范學院數學與計算機科學學院　江西 上饒 334001)

0　引　言

當前互聯網的快速發展和普及,一方面給人們的工作和生活帶來了很大的便利，另一方面也帶來了一定的網絡安全隱患。因此，網絡安全的研究將為確保網絡正常安全運行提供有力的保障，具有重要的現實意義。其中網絡異常的分析和研究是當前網絡安全領域中一個非常熱門的研究方向。網絡異常就是現有的網絡不能正常運行，產生網絡異常的因素錯綜復雜，有內部的網絡故障也有外來網絡攻擊的影響等。主要表現為網絡運行的故障、路由器設備故障、黑客入侵、拒絕服務攻擊、蠕蟲攻擊等[1-3]。

主成分分析PCA是一種統計分析方法，在高維數據的處理方面具有較強的優勢，是一種降維的主要工具，具有較好的無監督學習能力，該方法在網絡流量異常檢測方面得到了廣泛的研究[4-7]。Kobi Cohen等[8]采用主動假設檢驗的方法對網絡的異常情況進行了統計分析，并采用了一種漸進最優方法對網絡多元異常過程進行了研究，取得了較好的分析結果。文獻[9]基于主動學習技術對網絡異常進行了分析，提出了一種融合支持向量機和主動學習的網絡異常檢測方法，該方法不需要利用較多的標記數據，能夠有效地提升網絡檢測性能。

隨著云計算、大數據的發展，當前基于云網絡異常的檢測研究得到了高度關注和深入研究。李春林等[10]提出了一種面向云計算環境的網絡異常流量分組方法。該方法首先采用聚類分析技術對在云計算環境下產生的大規模網絡數據進行預處理，然后提取網絡數據聚類后的統計特征，并進行分組研究，最終得到網絡流量的分類結果和流量異常分組結果。文獻[11]采用支持向量機方法，提出了一種并行網絡流量的分類方法，具有較高的準確率。但是該方法的計算復雜，計算開銷大，難以實時檢測出網絡流量的異常情況，在實際應用中的推廣力度受限。基于此，文獻[12]提出了一種在線的自適應網絡流量分析方法，取得了較好的實時異常檢測效果。

本文受文獻[12]的啟發，同時根據文獻[13]指出的PCA在網絡異常檢測中出現的問題，即基于PCA的網絡異常檢測算法前提是假設網絡流量數據滿足高斯分布，且提取數據的非線性結構無能為力。因此，為了解決PCA在網絡異常檢測方面存在的問題，提出了一種基于核主成分分析的實時網絡流量異常檢測算法，最后通過仿真分析和比較，證實了該算法的有效性。

1　網絡數據流模型

一般來說，網絡異常的研究通常基于圖論或矩陣的數學方法來進行。一般采用矩陣對網絡的數據流進行描述，稱為網絡數據流矩陣。該矩陣可以反映一個網絡中所有源節點與目的節點之間的流量情況。網絡中的節點主要包括路由器、交換機、鏈路等。

網絡數據流矩陣的表示過程可以總結為：給定某個網絡，其已經部署了n個路由器節點。首先基于固定時間間隔對該網絡中任意一對節點之間的網絡流量數據進行測量，然后將測量后的網絡流量數據排列成一個N×T的矩陣X，其中X表示網絡中的數據流矩陣。其中T為測量的固定周期數，N表示在每個測量周期內測出的數據流值的數量；網絡數據流矩陣X中的第i列表示在第i個測量周期內的測量值向量，一般用Xi表示，第j行表示第j個節點對之間流量測量值的時間序列。

2　基于KPCA的異常檢測

在網絡數據流異常檢測的過程中，其核心步驟是建立用戶正常的行為模式，并且假設所有的網絡入侵行為都與正常行為不同。因此，建立網絡數據流的常態模型是前提條件，然后在此條件下來研究網絡數據流的行為模式，并與正常的行為模式進行比較，以確定它們是否正常。網絡數據流異常的檢測方式主要有兩種，即離線方式和在線方式。基于離線方式的網絡數據流異常檢測通常以批處理的方法建立常態模型，然后去發現在這批網絡數據流中是否存在異常。基于在線方式的網絡數據流異常檢測一般采用增量的方法建立常態模型，每步只對單個網絡測量值進行分析，以發現該測量值是否正常，并利用該測量值對常態模型進行迭代更新。

根據文獻[14]，網絡數據流可以看成是來自p個源的多變量時間序列S={Si(t)},i∈[1,p]。p表示網絡數據流的維度，每個源表示網絡中的節點(如路由器、鏈路等)。如果將網絡中的所有節點間的數據流測量值作為一個輸入向量Xi，那么Xi可以認為是存在于高維空間p中的一個多元變量，亦即數據流矩陣X就可以看成是高緯空間p中多元變量的時間序列其中T表示網絡測量的周期數。由于KPCA是基于核的特征提取方法中最有效的非線性特征提取技術之一，也是一種處理類似網絡數據流矩陣高維數據的有效技術手段，它通過引入核函數，將核矩陣代替測量值協方差矩陣。通過核矩陣求解特征值和特征向量，無需在整個特征空間中求解特征向量，相比主成分分析方法減小了計算量，又能進行非線性映射處理。因此，KPCA具有較好的降維性能。

2.1　Kernel PCA

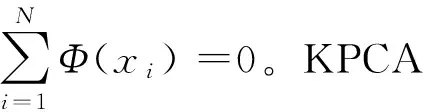
(1)

一般來說Φ(xi)Φ(xi)T求解困難，因此引入核函數來代替協方差，定義N×N維矩陣K：

K=[Ki,j]N×N=K(xi,xj)

(2)

(3)

(4)

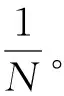
通過計算KC·V=λ·V，求解核矩陣KC的特征值λi和特征值所對應的特征向量V：

V=[vi]i=1,2,…,p

(5)

那么網絡數據流矩陣的主成分(即投影向量矩陣)可以表示為：

A=VTKC=〈KCV〉

(6)

將每個輸入向量Xi向正常子空間S投影，可以得到投影向量ai：

(7)

式中：Vk表示k個最大的特征值對應的特征向量組成的矩陣。顯然，輸入向量Xi能夠被投影向量ai在最小均方誤差意義下得到重構：

Xi=Vkai

(8)

(9)

其中：

(10)

首先使用式(7)將該輸入向量向當前的正常子空間S進行投影，得到投影向量at+1，然后計算重構Xt+1對應的殘余向量范數：

(11)

式(11)表示為殘余向量范數，該范數衡量原始輸入向量和重構輸入向量之間的誤差程度，預設一誤差閾值T，當誤差超過該閾值時，則認為輸入向量出現異常。

由于Q與當前特征空間相互垂直，因此將Q進行歸一化后，并添加到特征向量V中：

(12)

然后對A(t)作如下處理：

(13)

新的特征向量添加到已有的特征空間中，需要對已有的特征向量作旋轉變換處理，因此，對投影向量矩陣A′執行KPCA算法，獲得特征向量矩陣R，其中R表示已旋轉后的特征向量。

最后，特征向量矩陣V和投影向量矩陣A分別更新如下：

(14)

A(t+1)=RT(A′-η1)

(15)

2.2　異常檢測算法步驟

綜合以上分析，網絡數據流異常檢測算法的具體步驟描述如表1所示。

表1　基于KPCA的網絡異常檢測算法步驟

續表1

3　仿真結果與分析

本文采用Abilene數據集[4,6]，并使用Intel Core 4,4 GHz,8 GB內存，Windows 7的PC機在MATLAB 2010a上進行仿真實驗。其中Abilene數據集的具體描述見表2。表2中的數據集為因特網實際測量的網絡流量數據，包括網絡的異常流量數據和突發流量數據。常見的網絡流量異常包括:阿爾法(alpha)異常、(分布式)拒絕服務攻擊(DoS/DDoS)、端口掃描Port Scan異常、突發流(flash crowd)、Worms異常等。

表2　Abilene流量矩陣

為評價網絡異常檢測算法的性能，采用由誤報率和檢測率組成的接收機工作特性曲線(ROC)作為評價指標。其中誤報率指的是將網絡正常流量誤判為異常流量的比例，將其作為ROC曲線的橫坐標；檢測率指的是正常檢測出異常流量的比例，將其作為ROC曲線的縱坐標。接收機工作特性曲線體現的是對網絡檢測率和誤報率之間保持平衡的一種折衷，如果接收機工作特性曲線中的檢測率隨著誤報率的逐漸增加而快速靠近ROC曲線圖中的左上角。同時ROC曲線下方覆蓋的區域面積也越大，那么表明算法具有較好的檢測性能。因此，本節基于表2的4種數據集，采用這一評價指標與PCA網絡異常檢測算法[5]和文獻[9]進行了比較，其結果如圖1-圖4所示。

圖1　網絡異常檢測算法對實測數據DataSet1的檢測性能

圖2　網絡異常檢測算法對實測數據DataSet2的檢測性能

圖3　網絡異常檢測算法對實測數據DataSet3的檢測性能

圖4　網絡異常檢測算法對實測數據DataSet4的檢測性能

從圖1-圖4中可以看出，本文提出的基于KPCA的網絡異常檢測算法性能優于傳統的PCA檢測算法，當誤報率大于0.4時，與文獻[9]基于主動學習的網絡異常檢測算法性能相當。基于KPCA的網絡異常檢測算法主要引入了核函數，相比傳統PCA來說，對網絡流量數據的非線性特征具有較好的刻畫能力，而且同時具有較強的降維能力，在處理網絡數據流矩陣方面的性能優于傳統PCA。文獻[9]主要基于單分類支持向量機和主動學習對網絡異常進行檢測，該方法采用了無監督學習技術來建立支持向量機模型，并利用主動學習對該模型進行了參數優化，取得了較好的檢測結果。本文提出的算法在網絡數據的表示上比文獻[9]更為清晰。

4　結　語

在攻擊行為日趨多樣化的當今網絡環境下，如何有效地檢測出網絡中的異常行為是對網管人員的一大挑戰。針對網絡中流量的異常檢測，提出了一種基于核主成分分析的異常檢測算法。該算法以Abilene實測的網絡流量數據為研究對象，通過引入核函數機制，采用基于核的特征空間表示網絡流量數據，較好地提升了對網絡流量數據的非線性表示能力。仿真實驗結果表明提出的KPCA算法取得了較好的檢測性能。

[1] Bhuyan M H, Bhattacharyya D K, Kalita J K. Network Anomaly Detection: Methods, Systems and Tools[J]. IEEE Communications Surveys & Tutorials, 2014, 16(1):303-336.

[2] Chandola V, Banerjee A, Kumar V. Anomaly detection: A survey[J]. ACM Computing Surveys, 2009,41(3):1-58.

[3] Nguyen T, Armitage G. A Survey of Techniques for Internet Traffic Classification using Machine Learning[J]. IEEE Commun. Surveys Tutorials, 2008, 10(4): 56-76.

[4] Lakhina A, Crovella M, Diot C. Diagnosing network-wide traffic anomalies[J]. Acm Sigcomm Computer Communication Review, 2004, 34(4):219-230.

[5] Huang L, Nguyen X L, Garofalakis M, et al. In-network PCA and anomaly detection[C]//International Conference on Neural Information Processing Systems. MIT Press, 2006:617-624.

[6] Lakhina A, Crovella M, Diot C. Mining anomalies using traffic feature distributions[C]//Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications. ACM, 2005:217-228.

[7] 錢葉魁,陳鳴,葉立新,等. 基于多尺度主成分分析的全網絡異常檢測方法[J]. 軟件學報，2012,23(2)：361-377.

[8] Cohen K, Zhao Q. Active Hypothesis Testing for Anomaly Detection[J]. IEEE Transactions on Information Theory, 2015, 61(3):1432-1450.

[9] 劉敬，谷利澤，鈕心忻，等. 基于單分類支持向量機和主動學習的網絡異常檢測研究[J].通信學報,2015,36(11):136-146.

[10] 李春林,黃月江,牛長喜. 一種面向云計算的網絡異常流量分組方法[J].計算機應用研究，2014,31(12)：3704-3706.

[11] 裴楊,王勇,陶曉玲,等．基于SVM 的并行網絡流量分類方法[J].計算機工程與設計，2013，34(8) : 2646-2649.

[12] Khan F, Hosein N, Chuah C N, et al. Streaming Solutions for Fine-Grained Network Traffic Measurements and Analysis[J]. IEEE/ACM Transactions on Networking, 2011, 22(2):377-390.

[13] Ringberg H, Soule A, Rexford J, et al. Sensitivity of PCA for traffic anomaly detection[J]. Acm Sigmetrics Performance Evaluation Review, 2007, 35(1):109-120.

[14] Teixeira P H S, Milidiú R L. Data stream anomaly detection through principal subspace tracking[C]//ACM Symposium on Applied Computing. ACM, 2010:1609-1616.