GNSS接收機天線相位中心垂向偏差檢測

周廣勇　余慶濱

GNSS接收機天線相位中心垂向偏差檢測

周廣勇1,2余慶濱1

（1.廣東省計量科學研究院 2.廣東省現代幾何與力學計量技術重點實驗室）

為準確測出GNSS接收機天線相位中心垂向偏差，在超短基線靜態相對定位的基礎上，給出一種傾斜測量法。由臥軸多齒分度臺提供標準的旋轉角，將待測接收機天線傾斜多組角度，其余4臺接收機進行同步靜態觀測，解算出待測天線的多組坐標；再根據幾何關系得出絕對垂向偏差。該方法中配合的天線無需已知相位中心偏差。通過分析經不同的數據處理方法所得結果的差異，并與IGS發布的參考值進行比較，證實此方法測量精度較高，且有較好的可行性。

GNSS接收機；天線相位中心；傾斜測量

0　引言

全球導航衛星系統（global navigation satellite system，GNSS）作為一種高效的測量技術手段，因具有測站點間無需通視、全天候觀測、測量范圍大等特點，廣泛應用于測繪、國土、建筑工程、地球物理和地質災害監測等領域。GNSS水平方向測量精度較高，垂直方向測量精度相對較差。其中接收機天線相位中心垂向偏差是影響高程測量的因素之一，其偏差最大可達數厘米[1-2]，這對精度要求較高的變形監測、GNSS水準測量而言不容忽視。

目前，常見的相位中心檢測方法為我國測繪行業檢定規程CH8016—95和國家校準規范JJF1118—2004中規定的旋轉天線法，即在野外基線檢測場上，通過解算基線的較差來測定相位中心，該方法只能有效檢測天線相位中心垂向偏差的水平分量，而垂直分量無法檢出[3]；高差比較法配合精密水準儀可求得待測天線的垂向偏差；交換天線法需要配合檢測的另一個天線垂向偏差必須已知，否則求出的只是2個天線的相對垂向偏差[4-5]。

本文利用臥軸多齒分度臺提供的標準角，在1個垂直面對接收機天線進行多角度的傾斜狀態觀測，配合另外4臺接收機進行靜態相對定位，其他天線無需已知垂向偏差，就可解算求得待測天線絕對的垂向偏差。

1　檢測方法

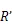
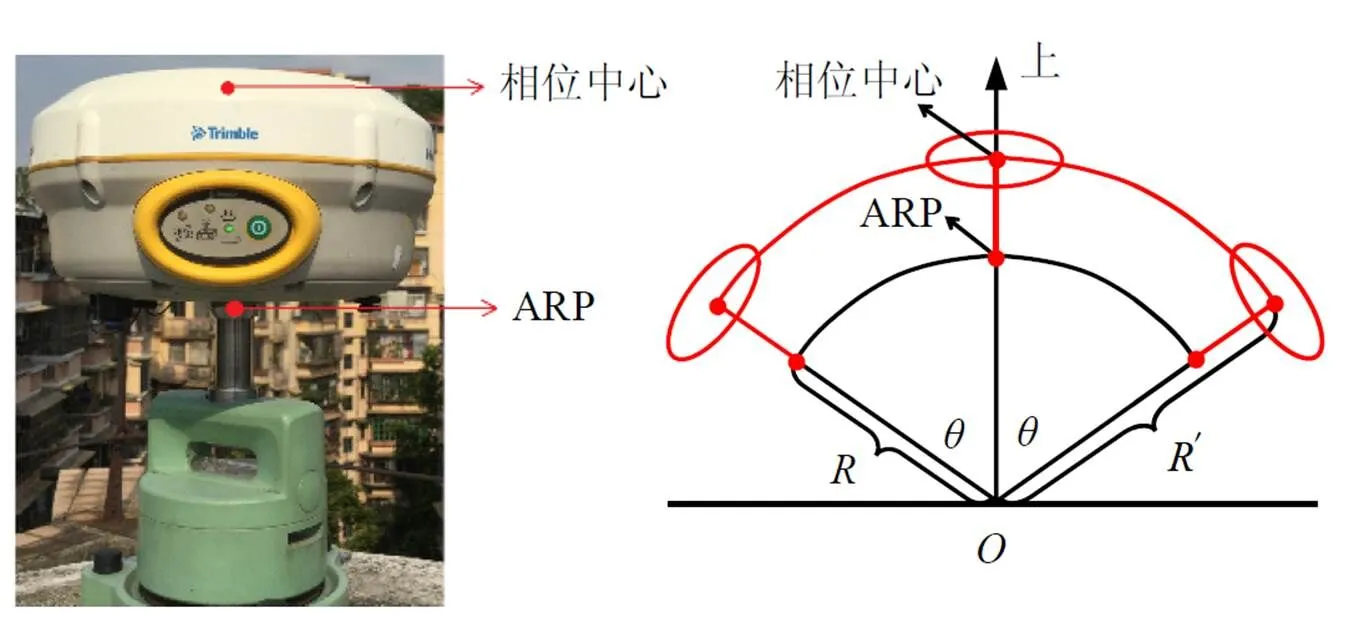
圖1　 垂向偏差檢測原理

2 檢測與試驗

在本院樓頂GNSS接收機超短基線場進行檢測實驗（見圖2），基線長3 m ~7 m，視野開闊、無干擾。將臥軸多齒分度臺（最大分度間隔誤差小于0.5″）置于基線場中心點觀測墩GA5，調平固定并鎖緊。用數顯卡尺（最大允許誤差為±0.04 mm）測得測量桿頂端到齒臺中心距離為238.2 mm。接收機選用5臺Leica GS15，待測接收機天線安置在多齒分度臺的測量桿上，其余4臺接收機分別安置在周圍點位GW1，GW3，GW5，GW7進行同步靜態觀測。多齒臺每傾斜旋轉一個角，觀測一個時段（時長約1 h，采樣率10 s，截止高度角15°）。解算基線網并固定某個配合點做約束平差[6]，求得待測天線每個角時的基線向量（即坐標差），可認為是天線的三維坐標。

3　數據處理及結果分析

經過解算求得各個點坐標及角度信息如表1所示。試驗中所用多齒臺為552齒，1格為（360/552）°，其中傾斜角為0時，天線處于垂直狀態，左右傾斜±15格、±30格……為傾斜狀態。解算結果為1頻率下的固定解。

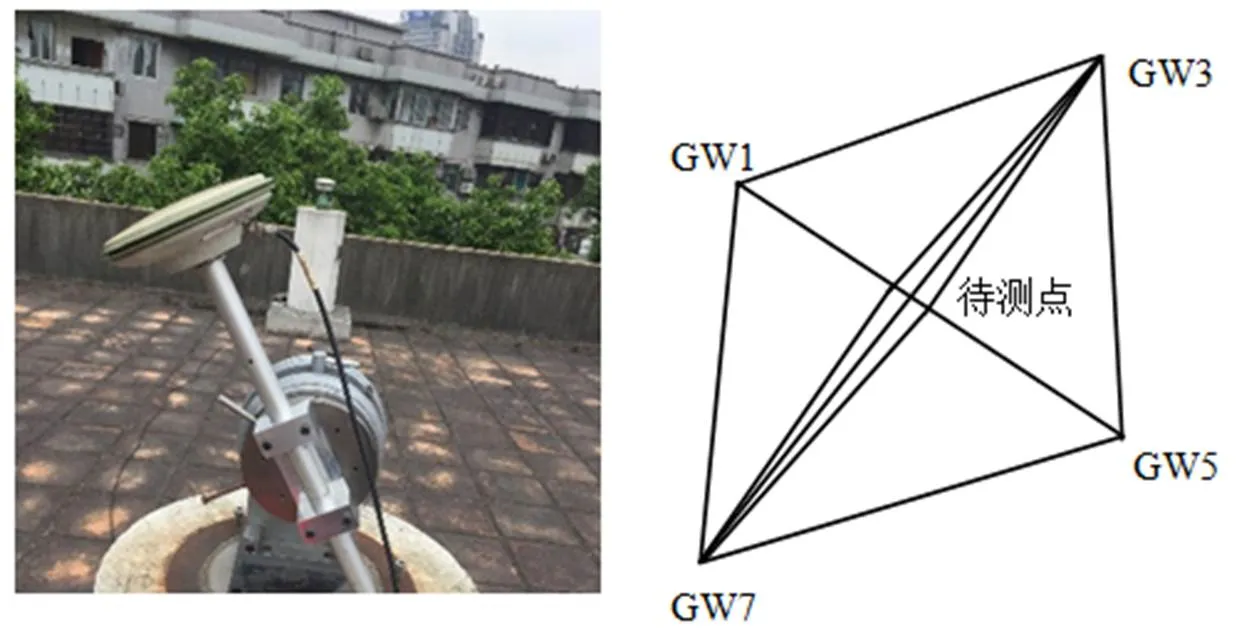
圖2 　實地試驗

3.1　利用點三維坐標直接擬合半徑

根據表1這些點的三維坐標，依據最小二乘法在空間擬合一個圓弧，求出圓的半徑。

空間圓實際上是空間圓球與空間平面的交線。因此先進行空間平面最小二乘擬合，再擬合空間圓球約束于此平面。設點位坐標為（x,y, z）（=1,2,…,），平面方程可表示為

將觀測坐標代入式(1)，可得到

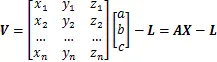
空間圓球的方程可表示為

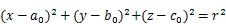
將觀測值代入式(3)，并線性化展開可得誤差方程為

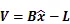
其中

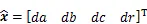
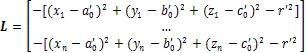
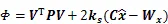
根據附有條件的間接平差法，可得法方程為

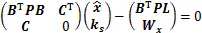
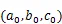
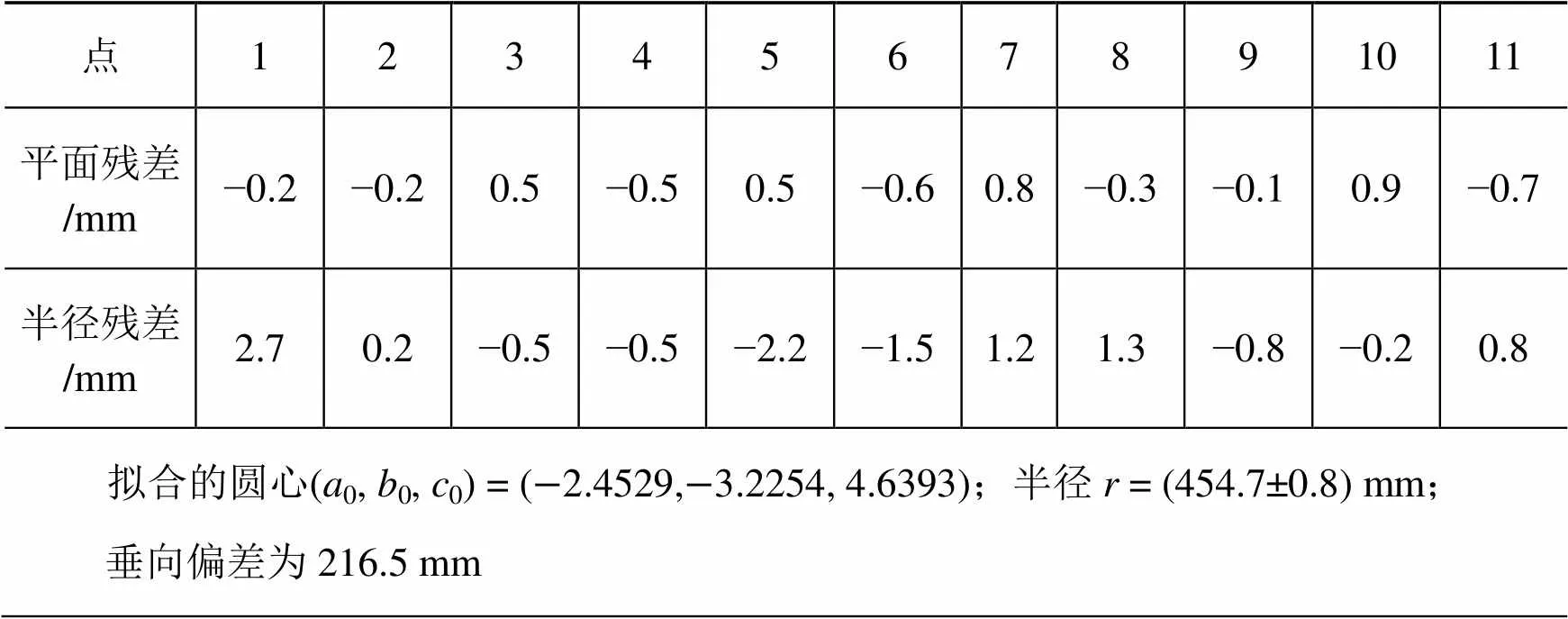
表2　 直接擬合結果及殘差

在國際GNSS服務組織IGS發布的天線文件[9]，查詢Leica GS15型號接收機的天線1頻率相位垂向偏差為202.05 mm，計算結果與其相差14.4 mm，以GNSS測量精度，不應出現如此大的差異。

3.2　 利用弦長計算半徑

考慮到GNSS接收機水平方向和垂直方向的測量精度不一致，因此，這些三維坐標的水平精度優于垂直精度。而且在直接擬合中舍棄了多齒臺標準的角度信息，故根據幾何關系采用測量精度最高的水平弦長直接求半徑的方式更為合理。由左右對稱分布的2測量點坐標計算其弦長為

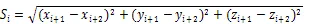
其中=1,3,5,7,9,…

由圖1可知，兩側相位中心點和點組成等腰三角形結構，圓心夾角為2，由余弦公式計算半徑為

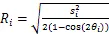
其中=1,3,5,7,9,…

由對稱分布的10個點得到5條水平弦長，計算半徑求平均值及其殘差如表3所示。

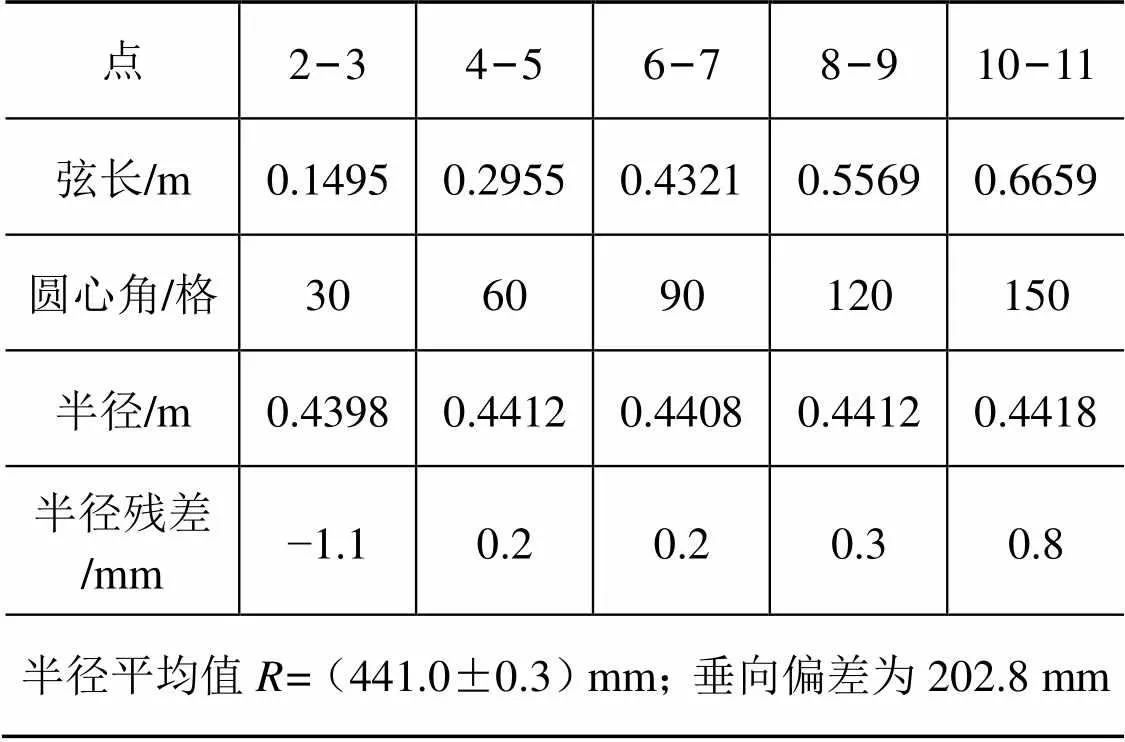
表3 　由弦長擬合結果及殘差

由表2和表3可以發現，2種計算方法得出的半徑結果分別為454.7 mm和441.0 mm，差異較大；同時發現采用三維坐標直接擬合半徑殘差較大，但由精度最高的水平弦長計算半徑的殘差小了許多，結果與參考值差異小于1 mm，因此第二種計算方法更可靠。

為進一步確認，用同樣的方法測試Leica AX1202天線和Trimble ZEPHYR天線，用弦長計算半徑得到垂向偏差結果分別為65.2 mm和55.9 mm，與IGS給出的參考值差異均小于2 mm。

4 　結語

針對GNSS接收機天線相位中心垂向偏差，進行了傾斜測量試驗，通過不同的數據處理算法，發現GNSS水平和垂直方向測量精度不一致對擬合結果影響較大。試驗表明：采用精度較高水平方向弦長數據能較好地算出旋轉半徑，根據幾何關系進而得到天線垂向偏差；且本方法不需要已知的天線相位信息，解算結果與IGS發布的參考值很接近，證實了本方法的正確性和可行性。該方法可用于實際高精度GNSS校準中，以進一步提高定位精度。本文研究處于初步階段，下一步將進行多種型號不同頻率下的試驗。

[1] Mader G L. GPS antenna calibration at the national geodetic survey[J].GPS Solutions,1999,3(1):50-58.

[2] 張磊,蘭孝奇,房成賀,等.天線相位中心改正對GPS精密單點定位的影響[J].測繪工程,2018,27(3):35-38,45.

[3] 張潤濤,馬德強.利用室外旋轉天線法估計導航衛星接收機天線相位中心偏差[J].全球定位系統,2016,41(4):17-21.

[4] 郭金運,徐泮林,曲國慶.GPS接收機天線相位中心偏差的三維檢定研究[J].武漢大學學報(信息科學版),2003,28(4): 448-451.

[5] 徐紹銓,高偉,耿濤,等.GPS天線相位中心垂直方向偏差的研究[J].鐵道勘察,2004(3):6-8.

[6] 李征航,黃勁松.GPS測量與數據處理[M].武漢:武漢大學出版社,2005,182-201.

[7] 武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2003.

[8] 李旭.空間圓擬合方法在地鐵洞門坐標計算中的應用[J].測繪與空間地理信息,2015,38(3):177-178,181.

[9] Ralf Schmid.Satellite/Receiver antenna corrections [DB/OL]. (2015-11-02) [2018-12-02]. http://acc.igs.org/antennas/igs05_ igs08_test.atx.

Vertical Deviation Detection of Antenna Phase Center in GNSS Receiver

Zhou Guangyong1,2Yu Qingbin1

(1.Guangdong Institute of Metrology 2.Guangdong Provincial Key Laboratory of Modern Geometric and Mechanical Metrology Technology)

On the basis of the relative positioning method，a new method is proposed to calibration the vertical offset of the antenna phase center. Field Tests were carried out. A Precise Angle Dividing Table with horizontal axis provides a standard angle to measure antenna tilted angles, with the remaining four receivers logging static observations simultaneously and finally get the coordinates of the antenna under test to fix the offset, then analyzed the different data processing methods and its differences, and compared with the IGS reference value, confirmed that this method has high accuracy and good practicability.

GNSS Receiver; Antenna Phase Center; Tilt Measurement

周廣勇，男，1984年生，碩士，高級工程師，主要研究方向：測繪儀器計量檢測。E-mail: zhougygz@126.com