細胞帶電分析中顯微細胞聚集度的數值表征方法

何佳熹, 鐘力生, 宋曉源, 張新桐, 靳勐, 邱閩晨, 高景暉

(西安交通大學電力設備電氣絕緣國家重點實驗室, 710049, 西安)

實現細胞膜電荷特性測量是國際生物電磁學研究領域的一個重要課題[1-4]。通過研究細胞膜的電荷特性,有望分析和表征細胞的功能變化,為相關疾病的檢測和治療提供物理手段,對深入認識電磁生物效應具有重要意義[5]。在細胞懸液中,細胞表面帶電狀況與細胞的團聚密切相關,因此在進行細胞顯微觀察時,觀測細胞團聚程度是判斷細胞帶電狀況的一種實驗手段。

目前,通過顯微觀察判斷團聚程度的方法大多憑借主觀識別[6-8],沒有統一的計算方法。要實現細胞團聚程度的測量和計算,首先需要對細胞位置和濃度進行判斷,有許多方法可用于對低濃度細胞的精確識別[9-11],但是當圖中細胞濃度很高,甚至人眼觀察都無法準確識別每個細胞的位置時,設計精確識別細胞的算法就較為困難。此外,顯微觀察時,視野中細胞數量通常存在一定差異,而細胞數量對于細胞團聚的影響又會給細胞團聚程度的觀測帶來主觀因素。

本文通過考察細胞顯微圖像灰度從而讀取圖像中細胞所處位置和密度,并由此通過計算細胞中心距倒數的平均值定義了細胞聚集度,建立了計算細胞團聚程度的方法。在此基礎之上,采用MATLAB軟件,實現了對顯微圖像的分析與重構,建立了使用細胞聚集度分析細胞表面電荷變化的方法,一定程度上解決了使用細胞聚集度定量判斷細胞帶電狀況的問題。

1　圖像的讀取與劃分

為了從細胞顯微觀測圖像中獲得細胞的聚集度,首先需要對圖像中細胞所處的位置和密度進行讀取。為此,本文設計了如圖1所示的圖像讀取步驟。

圖1　細胞圖像讀取步驟

1.1　顯微圖像灰度處理

為了簡化處理,本文先將如圖2a所示的顯微觀測圖像保存為如圖2b所示的灰度圖,使用二維灰度矩陣來存儲和處理圖像;再使用MATLAB軟件讀取圖像數據并按照像素保存成矩陣形式,其中矩陣每個元素的值都是0-1的雙精度浮點數,并在需要時將其顯示出來。

1.2　背景識別

如圖2b所示,首先要識別圖像中的背景部分,將背景和細胞加以區分。考慮到分散的細胞通常灰度分布區間較大,而觀察背景的灰度范圍通常集中在較窄的區間之內。本文采用讀取整個圖片灰度眾數的方法確定背景灰度,即認為整張圖片中按照像素出現次數最多的灰度為背景灰度。

(a)血細胞顯微觀測圖

(b)顯微觀測灰度圖

(c)顯微觀測網格剖分圖圖2　血細胞顯微觀察與網格剖分圖

1.3　劃分網格

實驗中的細胞實際形狀通常較為復雜且在很多時候難以精確識別,需要建立一種簡化的識別方法來確定細胞所處位置。本文將整個圖像按照一定邊長劃分為網格,根據細胞在圖像中的實際大小確定網格邊長,圖2b中觀測區域為1 024×1 280像素。像素單元對應邊長約為0.3 μm,每個細胞直徑約為15～20像素,因此為方便計算,將網格劃分為邊長為16像素的方格。細胞顯微觀測區域網格剖分結果如圖2c所示。

1.4　網格中細胞密度識別

識別每個網格中的細胞是圖像讀取過程中的關鍵一步,對于細胞位置和分布的精確識別直接影響到后續計算結果的準確性。一些文獻研究了處理紅細胞圖像的方法[10-11],但是對細胞的精確識別依舊較為困難且多數算法較為復雜。為此,本文給出了一種簡便地識別網格中細胞位置和密度的方法,滿足計算基本要求。

首先計算每個網格中的平均灰度,然后依據平均灰度與背景灰度之差是否大于預設值a來判斷該點是否存在細胞;接著需要判斷每個方格中的細胞密度。經過對圖像地分析發現,在細胞較少的網格中,細胞與邊界及細胞表面不同區域之間區分度較為明顯。因此,網格中不同區域灰度差別較大,而細胞較多處網格中的細節區分度較差,邊界較難區分,也即網格中的灰度差別較小。

(a)各參數細胞讀取結果

(b)人眼讀取結果與對應區域顯微觀測圖的對比

(c)a=0.15,b=0.1細胞讀取結果放大圖圖3　劃分讀取后細胞分布圖

雖然程序讀取和人眼讀取結果采用不同的標準,但在后續計算中,對細胞密度之和按概率分布進行了歸一化處理,因此在一張圖中只有格點密度與所有格點密度和之比會影響計算結果,只要其相對密度準確就可以保證計算結果的準確性,按照不同標準讀取密度并不會對后續計算結果產生影響。若要比較不同讀取結果的細胞相對密度,就需要先將圖3a中格點對應密度之和進行統一。為比較圖3a中各圖與圖3b的密度差,本文將圖3a中各圖細胞總數全都統一成與圖3b相同,并保持細胞相對密度不變。在此基礎上,本文按下式比較了圖3a上1/4部分和圖3b人眼讀取結果的二階偏差

(1)

式中:n為對應網格中總格點數;a、b分別為圖3a對應圖像和圖3b中各格點密度之和;A(i,j)、B(i,j)分別為圖3a對應圖像和圖3b對應的格點矩陣第i行第j列對應元素。Δ2越小表明兩矩陣之間差距越小。Δ2的計算結果如表1所示,可見a=0.15、b=0.1時,讀取結果和實際情況最為接近,既包含了圖2中有細胞的區域,又排除了背景區域,同時讀取的細胞密度和實際情況也有很好的對應關系。因此,本文最終選取a=0.15、b=0.1,放大結果如圖3c所示。

表1　不同參數讀取結果與人眼觀察的二階偏差

在進行以上處理后,為減少存儲空間和運算量,可以將細胞的位置保存在三列一維向量中,三列向量分別保存細胞的橫縱坐標和該坐標點的細胞密度,并且可將不存在細胞的點刪去。

2　聚集度的計算

2.1　聚集度計算模型

當考察外界因素對于細胞團聚程度的影響時,通常希望能夠排除視野內細胞數量不同造成的細胞團聚程度差異的影響。由于正態分布是最為常見的分布狀況,并且正態分布的標準差σ表示了分布的離散程度,這與本文中的聚集度具有類似的意義。因此,本文選取不同標準差σ的正態分布為例進行舉例說明。如圖4所示,標準差σ=3和σ=5,隨機取100個和300個散點的結果,同一張圖中顏色越深的點表示該點散點數越多。其中通過直觀觀察可以看出,當散點數相同的時候σ=3的散點團聚程度明顯小于σ=5的散點。通過直觀觀察也很容易認為當σ相同時,300個散點的團聚程度高于100個散點。這種由于視野內細胞個數增加造成的細胞團聚程度的增加,很多時候是在考察細胞團聚程度時希望避免的。

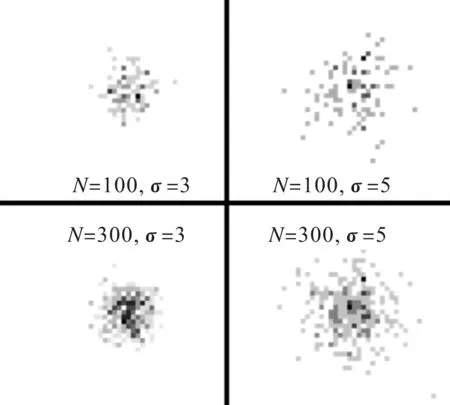
圖4　正態分布隨機散點圖

為計算細胞團聚程度,需要將細胞團聚程度抽象為一個數學問題。本文提出如下建模方法:假設細胞在圖2所示的二維平面上概率密度分布為f(x,y),則該問題抽象為構造一個關于f的參數聚集度δ來表示細胞團聚程度。根據圖2～圖4,以及前文提出的避免細胞個數對細胞團聚計算結果的影響,本文提出判斷細胞團聚的以下幾個要求。

(1)在細胞數量相同的情況下,與一個細胞鄰近的細胞越多,則細胞聚集度越大,如圖4中標準差較小的圖片具有較大的聚集度。即任意兩對細胞,若其中心距有d1δ2。

(2)細胞聚集度主要受鄰近幾個細胞的影響而與相對較遠處的細胞基本無關。根據圖2可以看出,在半徑約為10個細胞直徑范圍內的細胞數量對細胞聚集度影響較大,而相距在10個細胞直徑以上處的細胞數量對細胞聚集度影響較小,如圖2中左上角的細胞團聚和右上角的細胞團聚基本無關。為此若兩細胞中心距為1時對δ的影響為Δδ1,兩細胞中心距大于10時影響為Δδ2,應有Δδ1?Δδ2,或Δδ1>10Δδ2。

(3)由于顯微觀察存在很大的隨機性,當判斷外界因素對細胞團聚影響時,需要排除顯微圖片中細胞個數的影響。如圖4中散點數造成的聚集度影響應被排除,即當細胞分布f(x,y)確定時,δ應為一個與細胞總數N無關的數。

綜合考慮以上3點要求,本文定義細胞聚集度δ為整張圖片中細胞中心距的倒數的平均值,作為細胞團聚程度的表征參數,即

(2)

為在細胞散點圖中估計參數δ,用每個格點中細胞數與總細胞數的比代替概率分布函數,將積分改寫為求和,式(2)改寫為

(3)

式中:n(x,y)為(x,y)處細胞數;N為圖像中細胞總數。由于(x1,y1)=(x2,y2)時上述求和中分母為0,需要剔除每個細胞和其自身計算的情況,共N個,式(3)變為

δ=

(4)

即當估計參數δ時,只需要將每個細胞與其他細胞中心距倒數相加,然后除以細胞的兩兩組合數,即得到其細胞中心距倒數平均值的估計值。

在細胞所處位置取整之后,不同細胞間也會存在坐標相同的情況,即一個格點內存在多個細胞。當一個格點內存在多個細胞時,如果細胞在格點內呈平均分布,則式(2)中f(x,y)=1,但此時關于δ的積分難以解析計算。同時,考慮到格點內細胞不會完全重疊,直接令f(x,y)=1也和實際情況不符,對這種情況采取直接賦值處理,假設細胞平均中心距為0.5格,則其倒數為2。因此,當細胞處于同一格點時,利用式(4)進行累加時約定其累加值為2。

2.2　計算方法驗證

針對圖4中提出的4個正態分布圖形,本文按照以上提出的計算方法對其聚集度δ分別進行了計算,計算結果如表2所示。由表2可以看出,σ=3的圖像聚集度明顯大于σ=5的圖像,并且對于兩種不同的標準差有σ與δ乘積近似相等。這是由于δ是散點中心距倒數的平均值,σ是散點正態分布的標準差,正比于散點中心距;同時標準差相同的圖像,聚集度δ近似相等。由于正態分布取點的隨機性,不同圖像計算結果不可能完全相同,但是該計算結果已經很明顯地反映了聚集度δ隨圖中散點正態分布標準差的變化趨勢,且該結果僅與散點分布的聚集程度有關,與散點個數無關。因此,本文提出的計算方法滿足了2.1節中提出的建模要求。

表2　正態分布聚集度δ計算結果

3　使用聚集度表征細胞表面電荷變化

3.1　細胞聚集度表征細胞表面電荷變化

由于唾液酸是細胞表面負電荷的主要載體,使用唾液酸酶可以將唾液酸殘基從細胞表面去除,達到改變細胞表面電荷的作用[12]。為建立使用細胞聚集度分析細胞表面電荷的方法,本文使用4種不同濃度的唾液酸酶去除細胞表面唾液酸殘基,并對其進行了10次顯微觀測,圖5為其中一次的顯微觀測及之后的計算過程。

圖5　血細胞聚集度計算過程

為驗證血細胞團聚程度與唾液酸用量及細胞表面電荷的關系,并據此分析唾液酸酶對其表面電荷的影響,需要排除視野中細胞個數的影響,對血細胞團聚程度進行定量表征。實驗中,對10次觀測的結果利用式(4)計算細胞聚集度,并取其平均值和標準偏差,結果如圖6所示。由于唾液酸酶能夠去除細胞表面唾液酸,減少細胞表面帶電和細胞間的相互排斥作用,理論上會造成細胞聚集度的增加。考慮到顯微圖像選取存在一定的隨機性,實驗中標準差較大,且添加0.005 U/mL的唾液酸酶聚集度δ計算結果大于0.02 U/mL,但仍可以認為實驗結果在總體趨勢上反映了聚集度δ隨細胞表面電荷減小而增加的趨勢,同時從圖5中直觀觀察也可以得出類似的團聚程度變化規律。因此,可以認為當細胞聚集度δ增加時,表明細胞表面電荷減少,細胞間排斥作用減小,細胞趨于聚集;反之,當細胞聚集度δ減小時,表明細胞表面電荷增多,細胞間排斥作用增大,細胞趨于分散。

圖6　血細胞顯微觀察聚集度計算結果

3.2　聚集度表征細胞表面電荷變化的有效性

為驗證使用本文提出的方法計算細胞聚集度進而分析細胞表面電荷變化的有效性,本文使用ζ電位分析儀對細胞懸液的ζ電位進行了5次測量,實驗結果如圖7所示,由于細胞ζ電位為負值,為了使其變化趨勢更加明顯,圖中使用了其絕對值。

ζ電位是細胞表面雙電層中滑動層到溶液內部的電位差,正比于細胞表面電荷量[13-14]。實驗中,唾液酸酶去除了細胞表面唾液酸殘基,細胞表面負電荷減少,因而細胞表面ζ電位絕對值減少。同時由于細胞表面負電荷減少,細胞間相互排斥作用減弱,造成了細胞團聚作用增強。對比圖6與圖7中細胞聚集度δ與ζ電位變化曲線發現,當細胞表面ζ電位絕對值減小的時候,細胞聚集度表現出相似的上升趨勢,驗證了本文提出的使用細胞聚集度分析細胞表面電荷變化的有效性。本實驗定性描述了細胞聚集程度和細胞表面電荷及ζ電位的關系,但是其定量分析還有待進一步研究。

圖7　血細胞ζ電位的實驗結果

4　結　論

本文建立了一種基于細胞灰度圖計算細胞聚集度并由此推斷細胞表面電荷變化情況的方法,主要結論如下。

(1)提出了一種識別細胞所在位置和密度的計算方法;針對細胞數量不同的情況定義了細胞的聚集度,建立了基于細胞中心距倒數平均值計算細胞聚集度的方法;針對正態分布的情況驗證了該計算方法的可靠性。

(2)在此基礎之上,本文使用唾液酸酶改變細胞表面帶電基團,建立了使用細胞聚集程度分析細胞表面帶電狀況的方法,發現當細胞聚集度δ增加時,表明細胞表面電荷減少,細胞間排斥作用減小,細胞趨于聚集;反之,當細胞聚集度δ減小時,表明細胞表面電荷增多,細胞間排斥作用增大,細胞趨于分散。

(3)通過測量細胞ζ電位驗證了使用細胞聚集度反映細胞表面電荷變化的有效性,建立了使用細胞聚集度分析細胞表面電荷變化的數值計算方法。

本文方法可以在很大程度上排除視野內細胞數量對于細胞團聚程度的影響,從而使分析細胞表面電荷變化和細胞團聚程度的關系相比主觀觀察更具客觀性。

本文方法不僅可以用于細胞團聚程度和表面帶電狀況的表征,在相似的膠體或濁液中也存在類似的聚集度[15]計算問題,對膠體或濁液中分散相的分散程度或團聚程度及其表面帶電情況也可使用該方法進行類似分析。

參考文獻:

[1]MACGREGOR R J. A possible mechanism for the influence of electromagnetic radiation on neuroelectric potentials [J]. IEEE Transactions on Microwave Theory and Techniques, 1979, 27(11): 914-921.

[2]CASTELLARNAU M, ZINE N, BAUSELLS J, et al. Integrated cell positioning and cell-based ISFET biosensors [J]. Sensors and Actuators: B, 2007, 120: 615-620.

[3]QIU Minchen, ZHONG Lisheng, SONG Xiaoyuan, et al. Relaxation polarization model of SD rat tissues at frequency range 42 Hz-5 MHz [C]∥2016 IEEE Conference on Electrical Insulation & Dielectric Phenomena, Piscataway, NJ, USA: IEEE, 2016: 743-746.

[4]HE Jiaxi, ZHONG Lisheng, CHENG Lin, et al. The influence of ultrasonic electrokinetic polarization on the dielectric constant of erythrocyte suspension [C]∥2016 IEEE Conference on Electrical Insulation & Dielectric Phenomena. Piscataway, NJ, USA: IEEE, 2016: 751-754.

[5]李緝熙, 牛中奇. 生物電磁學概論 [M]. 西安: 西安電子科技大學出版社, 1990: 1-10.

[6]WICK P, MANSER P, LIMBACH L K, et al. The degree and kind of agglomeration affect carbon nanotube cytotoxicity [J]. Toxicology Letters, 2007, 168(2): 121-131.

[7]李志華, 劉芳, 王曉昌. 影響微生物聚集體的聚集度的因素分析 [J]. 環境科學學報, 2010, 30(3): 456-462.

LI Zhihua, LIU Fang, WANG Xiaochang. Analysis of the factors that influence the aggregation-degree of microbial aggregates in sludge [J]. Acta Scientiae Circumstantiae, 2010, 30(3): 456-462.

[8]AMINOFF D, BELL W C, SARPOLIS K, et al. Role of sialic acid in survival of erythrocytes in the circulation: interaction of neuraminidase-treated and untreated erythrocytes with spleen and liver at the cellular

level [J]. Proceedings of the National Academy of Sciences of the United States of America, 1977, 74(4): 1521-1524.

[9]龔聲蓉. 數字圖像處理與分析 [M]. 2版. 北京: 清華大學出版社, 2014: 199.

[10] HO Z P, LEE H J. A new algorithm for red blood cell characteristics image recognition [C]∥International Conference on Multimedia and Signal. Piscataway, NJ, USA: IEEE Computer Society, 2011: 303-307.

[11] MAJI P, MANDAL A, GANGULY M, et al. An automated method for counting and characterizing red blood cells using mathematical morphology [C]∥Eighth International Conference on Advances in Pattern Recognition. Piscataway, NJ, USA: IEEE, 2015: 1-6.

[12] 謝利德, 姚偉娟, 孫大公, 等. 神經氨酸酶對紅細胞膜的剪切彈性模量和表面粘度的影響 [J]. 中國生物醫學工程學報, 2001, 20(1): 33-37, 60.

XIE Lide, YAO Weijuan, SUN Dagong, et al. Effect

of neuraminidase on shear modulus of elasticity and surface viscosity of erythrocyte membrane [J]. Chinese Journal of Biomedical Engineering, 2001, 20(1): 33-37, 60.

[13] CHAMMAS P, EISENBERG S R. A microcontinuum model of electrokinetic coupling in the extracellular matrix: perturbation formulation and solution [J]. Journal of Colloid and Interface Science, 1994, 168(2): 526-538.

[14] 張玉亭, 呂彤. 膠體與界面化學 [M]. 北京: 中國紡織出版社, 2008: 179-183.

[15] 景允伸, 許宏, 常華, 等. 成核階段對沉淀法白炭黑團聚程度的影響 [J]. 山東化工, 2015, 44(9): 28-32.

JING Yunshen, XU Hong, CHANG Hua, et al. The influence of the nucleation stage in precipitated silica preparation process on agglomeration degree of silica [J]. Shandong Chemical Industry, 2015, 44(9): 28-32.