逆向工程數據處理的簡化方法
幸 鑫
逆向工程數據處理的簡化方法
幸 鑫
(重慶科創職業學院,重慶 402160)
文章所指的工程是反向創造的過程,即從現有的部分數據通過使用掃描或測量裝置重建其現有的部分。三維激光掃描儀已經變得更加準確、數據采集的速度急劇增加。但是,它每秒產生數千點,處理大量的數據是一個大問題。因此,必須減少獲得點數據,并將它轉換成生產過程所需的格式。本文提出的方法可以有效地減少點數據的數量,同時保持精度。
減少點數據;逆向工程;三維激光掃描儀;均勻和非均勻網格方法
一、激光掃描逆向工程
逆向工程過程包括點數據采集、噪聲過濾、數據簡化/排列/注冊、分割、曲線/曲面擬合和三維表面模型生成[1]。數據采集被認為是反求工程的關鍵步驟,因為原始數據的質量決定了結果表面的質量。一旦原始數據在掃描過程中產生噪聲數據點,即所謂的離群值或峰值,必須通過刪除、平滑和合并等預處理予以消除,從而提高點數據的質量。消除峰值的方法如下:
(1)考慮兩個連續點之間的角度,并且與前一個大于給定值的點成一個角。
(2)峰值點可以移到中值。
(3)在允許的距離內,點可以沿指定的軸向上或向下移動到指定的水平位置[2]。
刪除峰值之后,應考慮掃描裝置的特性來執行數據縮減方法。
1.三維激光掃描儀
3D激光掃描裝置獲取部分表面信息,通過激光束從表面發射和CCD相機感應來接收。激光束通常可分為點型和條型,條型掃描儀照射到表面上可以得到多個點,而點型掃描儀一次只能獲得一個點。根據配置不同,激光掃描設備可分為三類,如圖1所示。
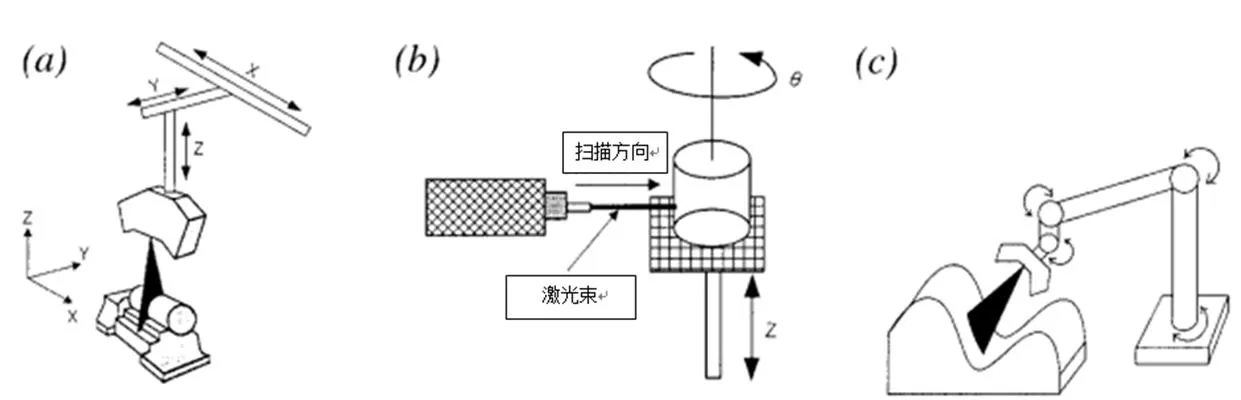
圖1 激光掃描設備分類
當激光探頭掃描一個物體時,由CCD相機感測到的光線作為強度數據存儲在像素中,然后通過圖像處理和三角測量方法將此信息轉換為掃描點的三維坐標。圖2顯示了三角測量法的原理。
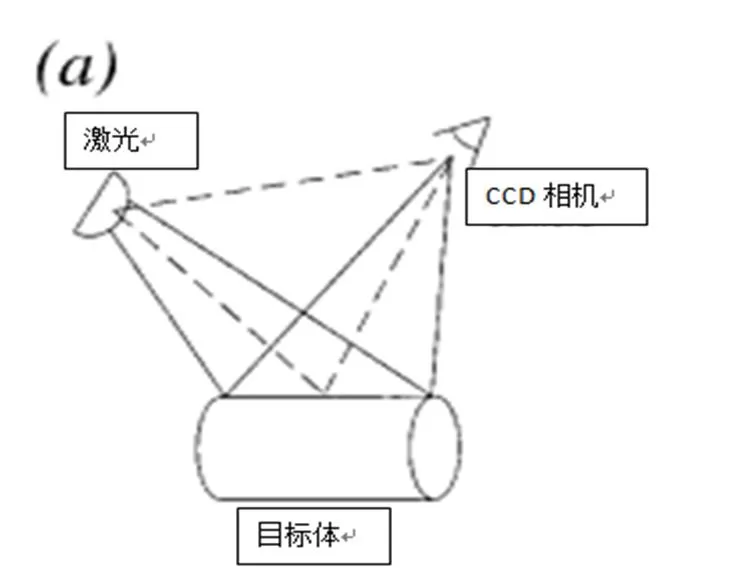
圖2 三角測量方法
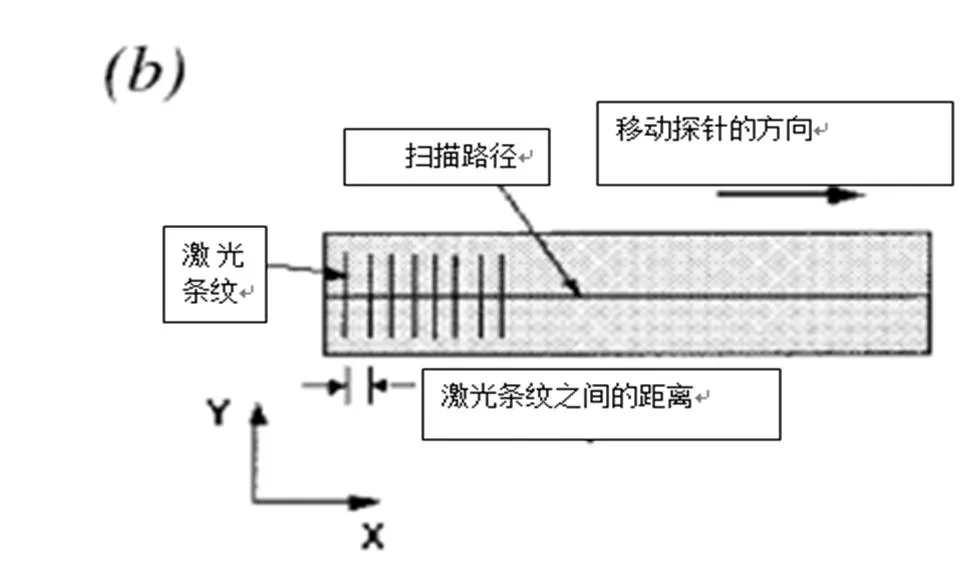
圖3 掃描操作
本文中使用的激光掃描儀屬于第一種類型,它使用一個探測器,沿著圖3所示的掃描路徑移動時發出一系列激光條紋。三維點坐標x和y是根據探頭直接由運輸機構控制的位置獲得,此時x和y值是可靠的,但一般的z值顯示精度差,因為Z值由CCD攝像機處理檢測射線測定,Z軸的誤差范圍從0.01mm到0.10mm,主要取決于掃描設備的質量。因此,由激光掃描儀產生點云數據時,應該控制z軸誤差以產生精確的表面。
2.使用均勻網格的點數據縮減方法
通過將數據劃分為網格并從每個網格中采樣代表點,可以減少點數據的數量。由于激光掃描儀的特點,z值誤差大,所以在網格中使用中值濾波。首先,網格面是由與掃描方向垂直的大小相同的網格組成,數據縮減率由網格大小決定,網格尺寸越小,整個點云中采樣的點越多。在創建一個均勻的網格平面之后,所有的點都被投影到網格平面上,并且每個網格被分配相應的點。其次,從每個網格中選擇一個點中位數篩選規則[3]。每個網格中的點按照到網格平面的距離進行排序,并選擇一個位于中間的點,如圖4所示。
使用均勻網格的中值濾波,那些被認為是噪聲的點很可能被丟棄。如果掃描的表面垂直于掃描方向,則該方法表現出更好的性能。這種方法對于保持原始點的數據是很好的,因為它選擇點而不是改變點的位置。均勻網格法特別適用于表面相對簡單的零件必須快速減少數據的情況。
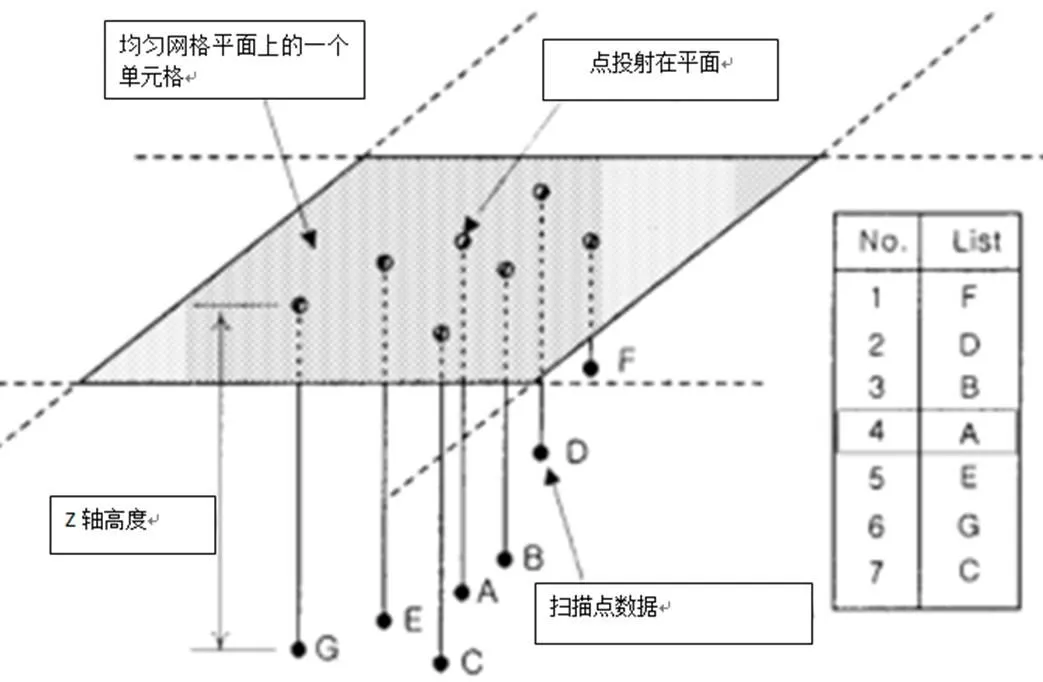
圖4 均勻網格方法
二、使用非均勻網格的數據縮減方法
應用均勻網格法時,由于沒有考慮零件的形狀,所以零件形狀急劇變化的一些點,可能會丟失。本文提出了非均勻網格方法,其中網格的大小可以根據零件的形狀而變化。根據測量數據的特點提出了兩種非均勻網格方法:單向和雙向。
1.單向非均勻網格法
在單向非均勻網格法中,使用角度偏差法從部件表面獲取的點云中采樣,如圖5所示,角度偏差法根據由連續的三個點構成的矢量,例如(x1,y1),(x2,y2),(x3,y3)計算的角度來選擇點。
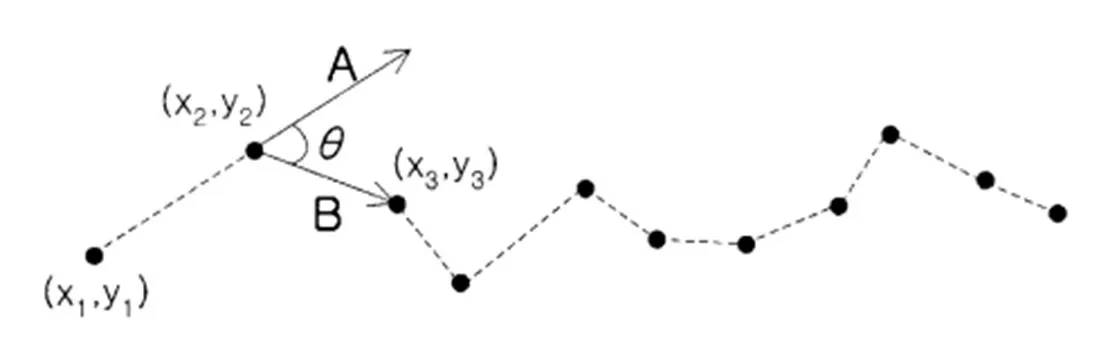
圖5 角度偏差法
角度表示曲率,當角度小時曲率小,反之[4],使用這些角度,可以提取高曲率的點。由角度偏差提取的點表示高曲率區域,并且在數據縮減期間必須保留它們以精確地表示零件形狀。因此,如圖6(a)所示,在使用角度偏差法提取點之后,根據提取的點來劃分沿v方向的網格,在劃分網格時,如果網格大于用戶預定的最大尺寸,則進一步劃分網格以使其不超過最大網格尺寸圖6(b)。然后,將中值濾波應用于每個網格中的點。與均勻網格方法相比,該方法在保持零件形狀精度的同時能夠更有效地減少點數據。

圖6 單向不均勻網格生成
(2)雙向非均勻網格法
在雙向非均勻網格法中,計算各個點的法向矢量,并根據這些信息進行數據縮減。首先,在確定點的法向矢量時,使用相鄰三角形的法向矢量。如圖7所示,對于點p,六個相鄰存在三角形,并且點N的正常值可以使用式(1)。
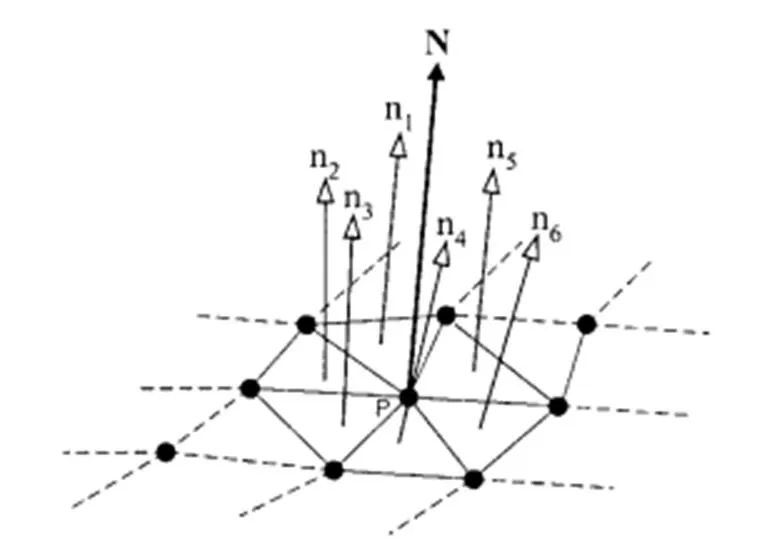
圖7 正常值計算
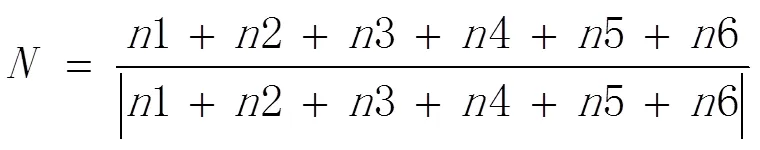
在計算所有點的法向量時,生成網格平面,網格大小由用戶定義并取決于給定零件形狀的預期數據縮減率。如果需要大量減少點數據,網格的大小將會增加;反之,通過投影網格平面上的點,對應的每個網格的點被分組,并且這些點的正常值被平均。作為網格細分的標準,使用點正常值的標準偏差。考慮到部件形狀和期望的點數據縮減比率,標準偏差的水平是預定的。如果網格中的標準偏差很大,則表示與網格相對應的零件幾何形狀是復雜的,因此需要進一步細分網格以便采樣更多的點。如果網格的標準偏差大于給定值,則網格被細分為四個單元格。這個過程重復進行,直到網格的標準偏差小于給定值,或者網格尺寸達到用戶指定的最小限度。與單向方法相比,這種雙向方法提取更多點,從而更準確地表示零件的形狀。
三、實驗結果
提出了基于非均勻網格的點數據縮減方法,使用不同類型的零件表面進行了測試。在應用簡化算法之前,從初始點云中去除異常值或峰值。
1.均勻網格到簡單的表面
在討論所提出的數據縮減方法的實驗結果之前,使用均勻網格方法來顯示由激光掃描儀獲得的點云的中值濾波的有效性。表1中總結了原始點云均勻網格和均勻采樣點的平滑度和點數。

表1 平滑度的比較
結果表明,使用中值濾波將z軸上的點云誤差范圍降至最小。
2.非均勻網格自由曲面
由于網格大小的靈活性,非均勻網格方法更有效地處理自由形狀的物體,如較小的網格用于高度彎曲和細節的區域,較大的網格用于平面和接近平面的區域。為便于比較,其他數據簡化方法也適用于同一模型,結果匯總在表2中。
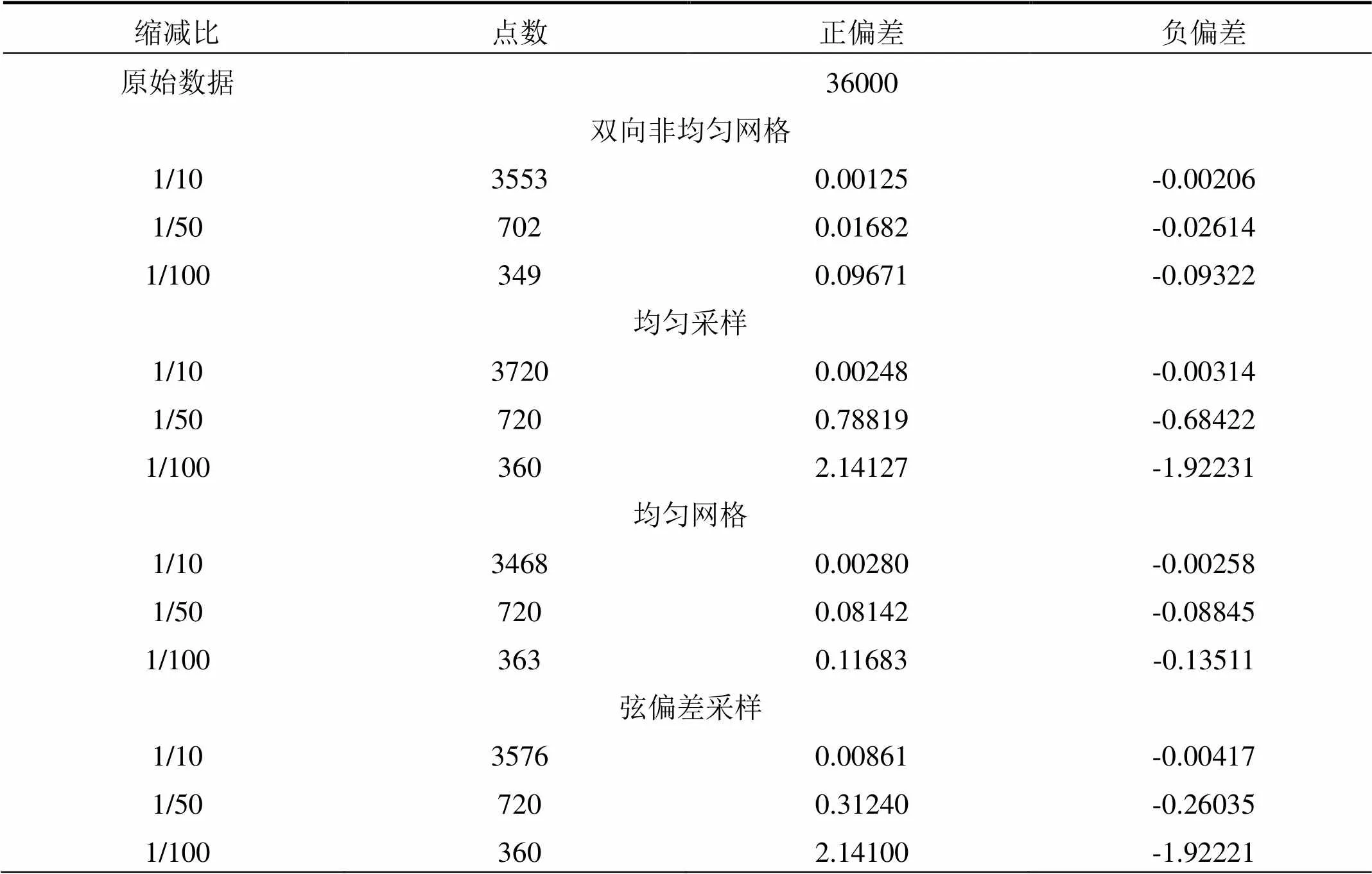
表2 樣品偏差匯總表(單位:mm)
隨著縮減比的增加,縮減點數據組與原始模型的偏差更大,然而對于所有級別的減少,雙向非均勻網格方法顯示的偏差比其他方法更少。而且即使增加減少,考慮精確度和點數,確定最佳的數據縮減率取決于在零件形狀上。雖然每個方法只有一個自由形式模型被測試,但是這個研究證明了非均勻網格方法在減少自由形狀零件的點云數據方面的有效性。
四、結論
本文研究了用激光掃描儀采集點云數據的過程,隨著掃描設備技術的提高,數據采集的速度可能會增加,這將必須自動增加點數據量的處理。從激光掃描中出現的零件形狀和z軸誤差的角度出發,提出并實現了采用單向或雙向不均勻網格的數據壓縮方法。將所提出的方法應用于具有自由形狀的樣本模型,并將結果與其他常規方法進行比較分析,所提出的方法證明了可以在保持點數據質量的同時有效地執行減少。
[1]B. L .Curless. “New Methods for Surface Reconstruction from Range Images”,PhD thesis[M].Stanford University,1997.
[2]Data Sculpt User’s Manual Version 4.0[Z].Laser Design,1995.
[3]A. D. Marshall and R. R. Martin. Computer Vision Models and Inspection[J].World Scienti?c,1993.
[4]B. Hamann and J. Chen. Data point selection for piecewise linear curve approximation[J].Computer Aided Geometric Design,1994(11): 289–301.
Simplified Methods for Data Processing in Reverse Engineering
XING Xin
(Chongqing Creation Vocational College, Chongqing 402160, China)
The project referred in this article is the reverse-created process which means to reconstruct its existing part by existing partial data through using scanning or measuring equipment[1]. 3D laser scanners have become more accurate and the speed of data acquisition has dramatically increased. However, there is a big problem that it generates thousands of points per second and handles large amount of data. Therefore, in order to reduce the number of points obtained and convert it to the format required by the production process, this paper proposes a method can effectively reduce the amount of point data while maintaining the accuracy.
reduced point data; reverse engineering; 3D laser scanner; uniform and non-uniform grid method.
TP391.7
A
1008—6129(2018)01—0097—05
2018—01—08
幸鑫(1991—),女,重慶人,重慶科創職業學院,助教。

