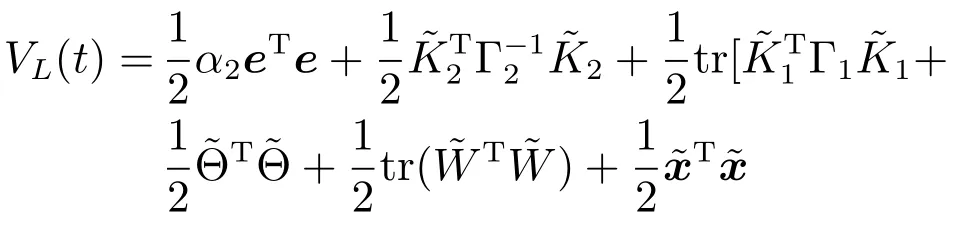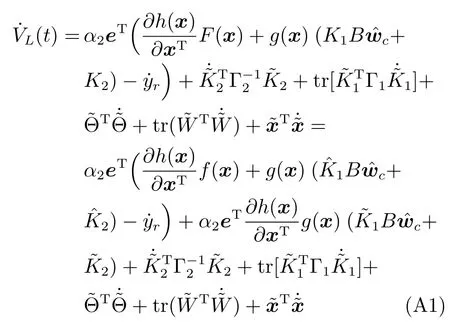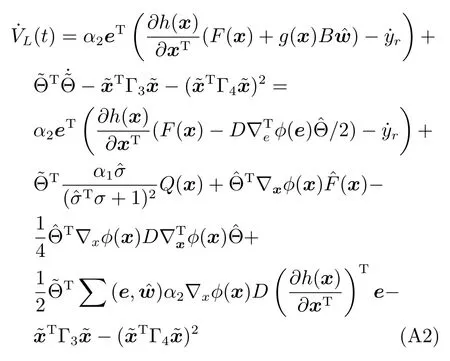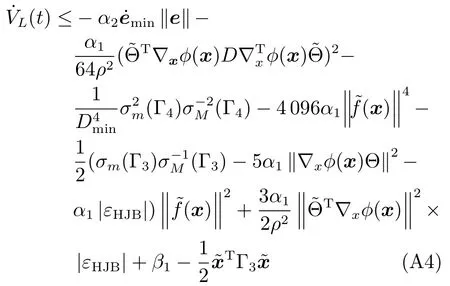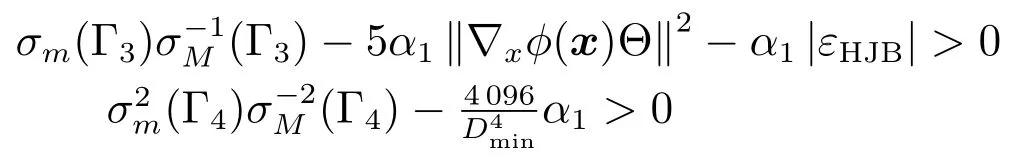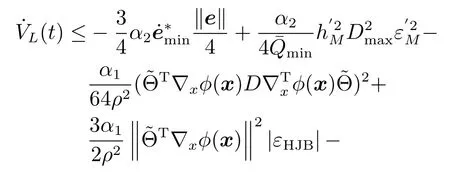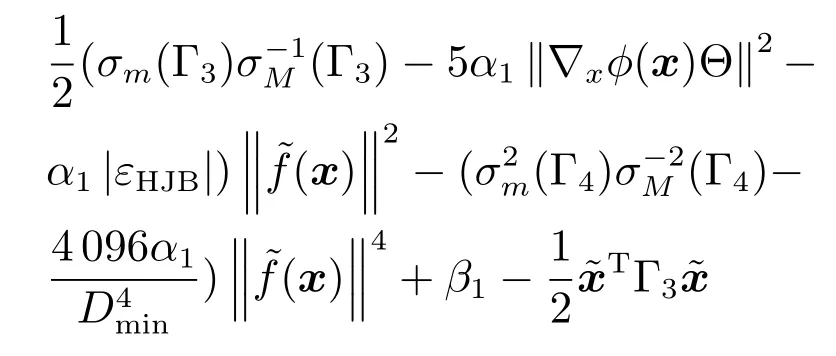執行器故障不確定非線性系統最優自適應輸出跟蹤控制
張紹杰 吳雪 劉春生
隨著技術的進步,使得具有強非線性、大范圍變化的非線性動力學系統越來越多.用精確的數學模型描述這類系統的動態特性是不現實甚至是不可能的.人們在對這類系統進行數學建模時,通常在某確定點的微小變化范圍內將非線性系統描述為線性系統,或用低階系統代替高階系統等方法近似,這都會或多或少地使系統存在建模誤差及不確定性.除了模型不確定性外,環境的變化、內部參數的變化、未知的外界擾動以及未知執行器故障也會造成被控系統的不確定性.如果對于系統的控制器設計及分析中沒有考慮這些不確定因素,所設計的控制系統將很難保持所期望的性能,甚至使系統失去穩定性.因此,非線性系統的執行器故障容錯控制得到了廣泛的研究[1?13].基于故障檢測與隔離(Fault detection and isolation,FDI)的容錯控制[7?9]和自適應補償控制[10?13]是兩種典型的容錯控制方案.基于FDI的方法需要確定系統故障信息并利用故障信息重構控制器.基于自適應補償控制方法設計的控制律不受故障診斷誤差的影響,不需要在系統故障時重新調整控制律的形式、結構簡單,且易于從理論上證明系統的穩定性和跟蹤能力,因此這種方法得到了廣泛的研究.
文獻[10]提出了一種針對具有執行器故障的多輸入單輸出(Multi-input single-output,MISO)非線性系統的反步自適應補償跟蹤控制方法.文獻[2,11?13]將該方法擴展到了多輸入多輸出(Multiinput multi-output,MIMO)系統,其中文獻[12]考慮了更多的執行器故障類型,文獻[13]進一步考慮了系統的不確定性.但上述方法均未考慮容錯控制系統的性能指標,不能從理論上表明所設計控制律的控制效果.文獻[14]考慮了系統的動態性能,但不能保證性能指標選取的最優性能和合理性.
自適應動態規劃[15?20](Adaptive dynamic programming,ADP)是近年來得到廣泛關注的智能優化控制方法,2002年,Murray等[21]提出了針對連續系統的迭代ADP算法.針對系統狀態調節問題,Vamvoudakis等[22]采用神經網絡構造評價網絡和控制網絡,通過在線自適應的方式調節神經網絡權值,使得評價網絡和控制網絡的輸出各自逐漸逼近最優代價函數和最優控制函數.Dierks等[23]設計了一種新的ADP結構,該方案不需要控制網絡,只通過評價網絡完成控制作用.少數文獻[24?29]針對系統的最優跟蹤問題進行了研究,文獻[24?26]研究了系統的狀態跟蹤控制問題,針對輸出跟蹤控制問題,Zargarzadeh等[27]針對一類MISO非線性嚴反饋系統,提出了一種通過構造在線自適應評價器,得到系統近似最優解的控制方法.在此基礎上,文獻[28?29]考慮了系統動態未知的MISO非線性嚴反饋系統的最優輸出跟蹤問題.
雖然采用ADP方法研究非線性系統的最優控制已經有了較多的研究成果,但是多數研究成果僅適用于嚴反饋系統等特殊的非線性系統,相關控制方法較少考慮存在系統故障時的控制問題;系統控制結構通常由前饋控制和反饋控制兩部分組成,結構復雜.針對現有研究成果的上述缺陷,本文針對一類具有不確定性的MIMO連續時間非線性系統的輸出跟蹤控制問題,考慮執行器失效、卡死以及兩者的組合故障,采用神經網絡估計系統不確定性,設計基于ADP的最優自適應補償控制律.該方法不需要前饋控制項,只采用評價網絡求解最優跟蹤控制律,通過李雅普諾夫理論證明了系統的跟蹤誤差一致最終有界.
1 問題描述
考慮一類如下描述的多輸入多輸出連續非線性系統[13]
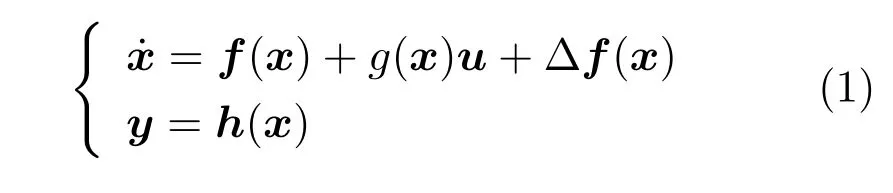
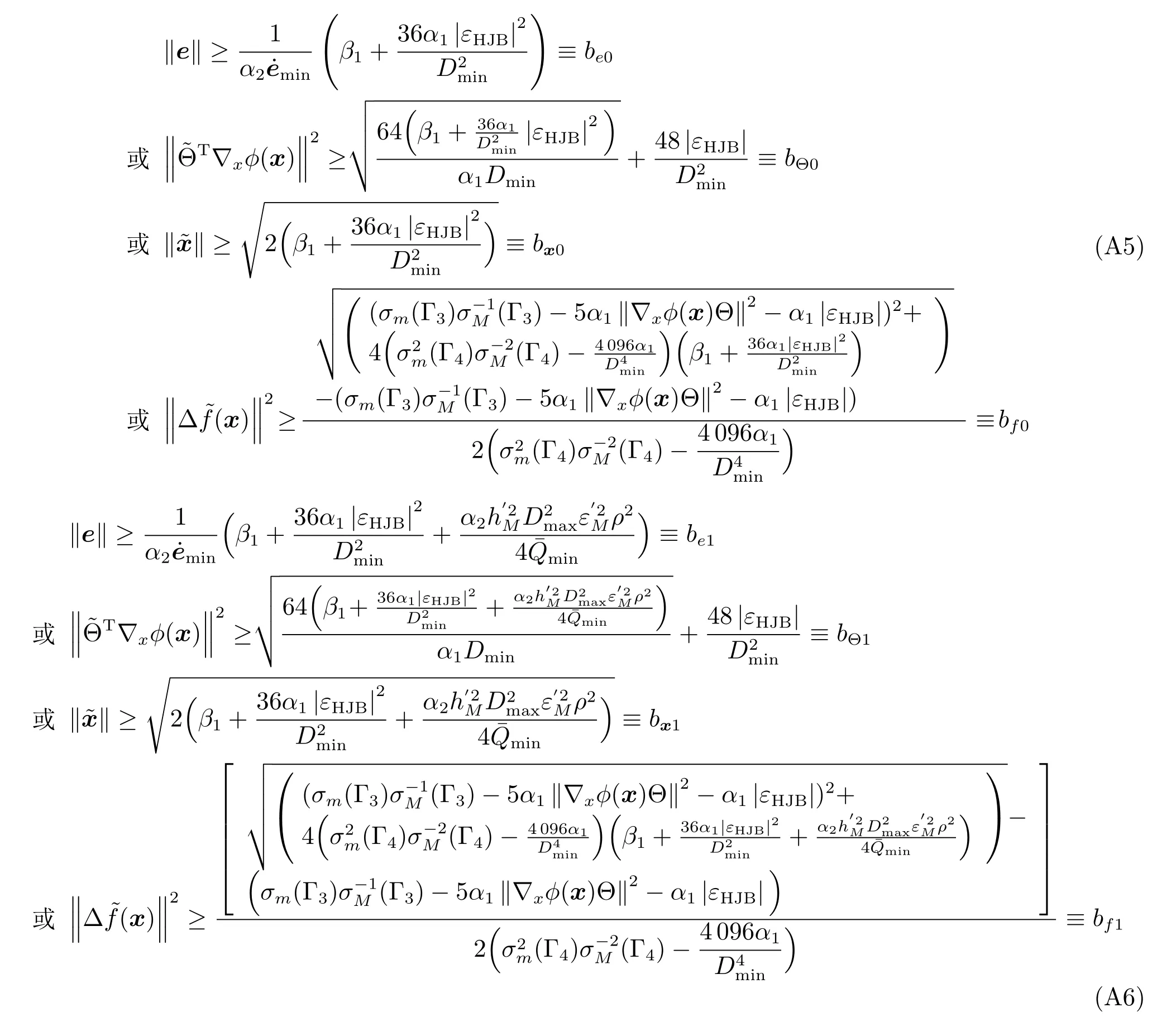
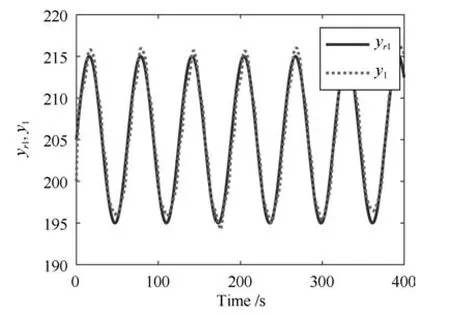
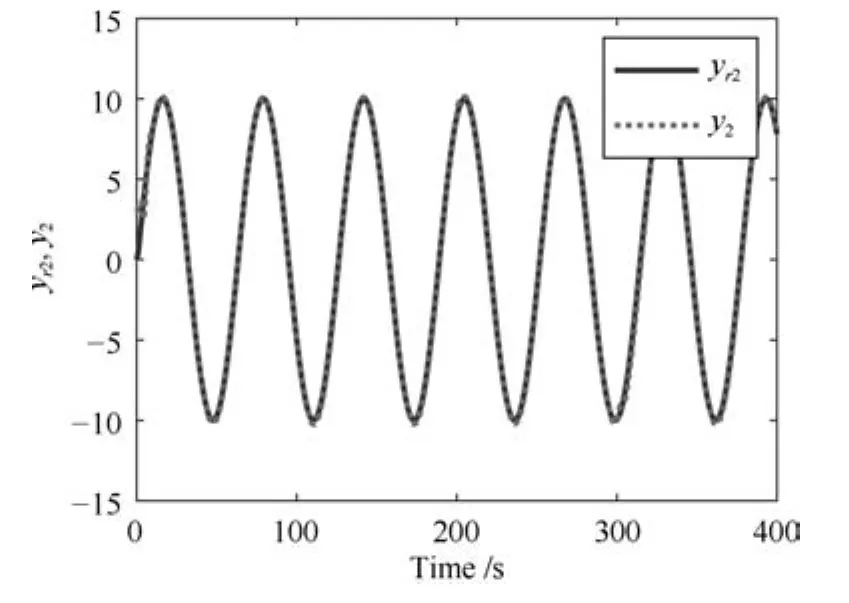
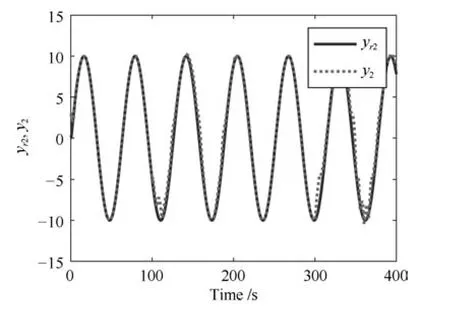
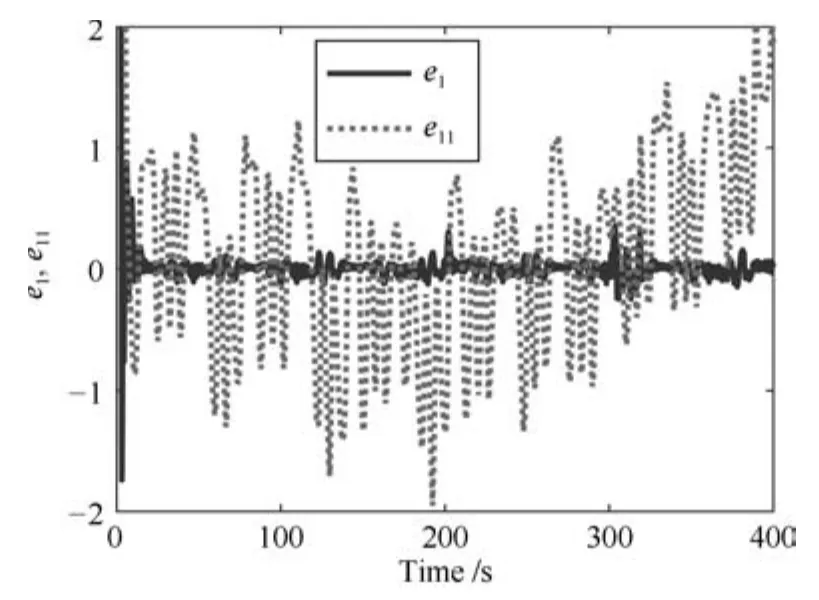
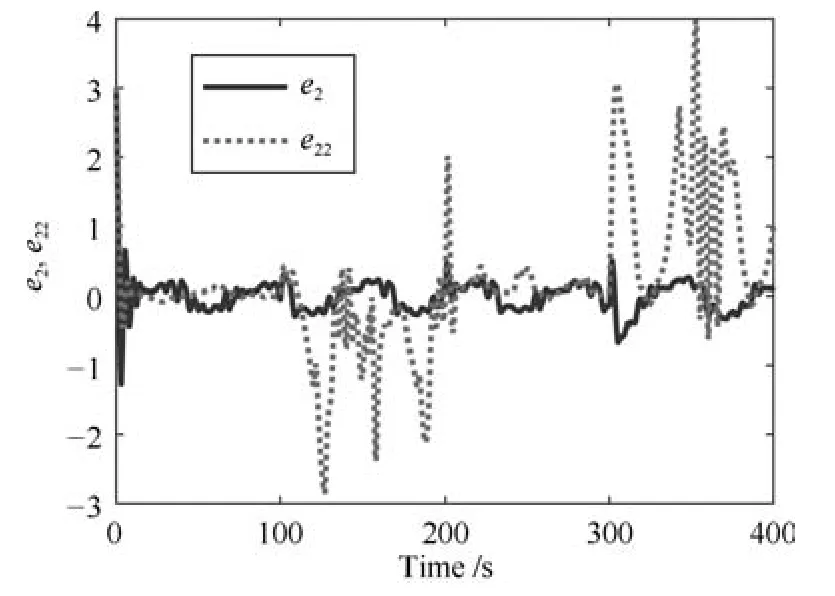
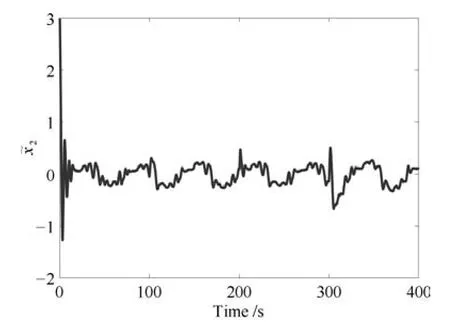
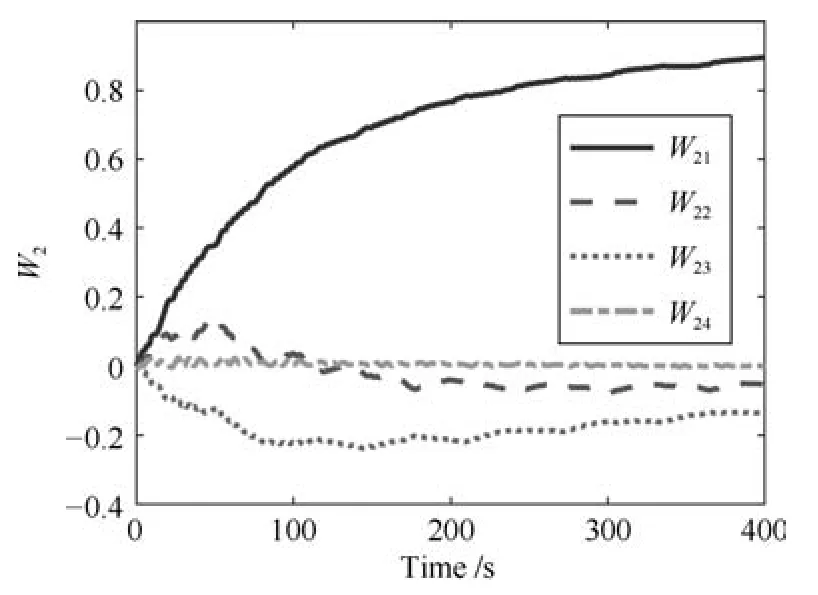
其中,x∈Rn是系統的狀態向量;f(x)∈Rn,g(x)∈Rn×m和h(x)∈Rq是關于x的充分光滑的非線性函數;u=[u1,···,um]T∈Rm是系統執行器的控制輸入;?f(x)∈Rn為系統的不確定項;y∈Rq(0 考慮執行器失效、卡死及其組合故障,故障形式可表示為 其中,ui和uci分別是系統第i個執行器的實際控制輸入和設計的控制輸入;λi(0≤λi≤1)和i是未知常數,分別代表系統第i個執行器發生失效故障時的有效比例以及卡死故障時的卡死位置;ti是代表故障發生時間的未知常數. 當發生如式(2)所示的執行器故障時,可以將系統控制信號u表示為 假設1.在系統(1)發生式(2)形式的執行器故障時,依然可以利用無故障或故障后仍可用的執行器控制系統完成任務. 假設1保證了系統容錯控制律的存在性,是可以對系統進行容錯控制的必要條件. 為了處理執行器冗余的問題,將m個執行器分在q(1≤q 上式表示dk(k= 1,···,q)個輸入uk1,uk2,···,ukdk分在第k組中,d1+d2+···+dq=m. 由執行器分組結果,可將控制輸入記為 其中,w(t)=[w1(t),w2(t),···,wq(t)]T∈Rq×1是執行器正常時待設計的控制律,wc(t)=[wc1(t),···,wcq(t)]T∈Rq是執行器故障時的控制律表示形式.是控制分配矩陣,,其中,bj是用來調節對應的系統執行器對控制輸入影響的比例參數.根據式(5),可將系統(1)改寫為 取yr(t)=[yr1,yr2,···,yrq]T∈Rq為系統參考輸出,系統輸出跟蹤誤差記為 假設2.系統狀態可控,且在x=0時,f(0)=0,非奇異. 假設2中系統狀態可控是設計不確定性估計器的前提,其他假設條件是系統可以求解最優控制的前提. 定義系統(7)的代價函數為 其中,Q∈Rq×q,R∈Rq×q是正定常數矩陣,并且存在連續控制函數w(t)使得系統輸出跟蹤參考輸出. 把式(8)代入式(9),可得用x(t),w(t)和yr(t)表示的代價函數 本文的研究目標為針對具有執行器故障(2)的系統(1)設計最優自適應補償控制律,通過求解使代價函數(9)最小的近似最優控制輸入,使得系統(1)能夠實現對參考輸出信號yr的跟蹤. 由于系統動態方程中含有不確定項?f(x)=[?f1(x),?f2(x),···,?fn(x)]T, 本文設計神經網絡估計器來估計 ?fi(x)(i=1,2,···n),?fi(x)可以表示為 式中,θi(x):Rn→Rmi是基函數,Wi∈Rmi是權值向量,εfi是估計器的估計誤差,滿足,.神經網絡對不確定項?fi(x)的估計可以表示為 定義系統狀態xi(i=1,2,···,n)的估計為 設計神經網絡權值調整律為 其中,Γ3=diag{Γ31,···,Γ3n},Γ4=diag{Γ41,···,Γ4n}. 表明系統的狀態估計可以逼近實際系統狀態,可實現對?f(x)的逼近. 其中,r(x,w)=(h(x(t))?yr(t))TQ(h(x(t))?yr(t))+wT(t)Rw(t),Vx(x)是V(x)對x的偏導.因為使代價函數(10)最小的最優控制輸入也使哈密頓函數(16)最小,所以可以通過求解方程?H(x,w)/?w=0,得到最優控制輸入,記為 式中,Q(x)=(h(x(t))?yr(t))TQ(h(x(t))?yr(t)).當控制輸入為最優控制輸入w?(t)時,記系統的閉環動態方程F(x)+g(x)Bw?滿足 其中,K?為常數. 設計在線神經網絡把代價函數(10)表示成 其中,Θ∈RL是在線神經網絡的目標權值向量,φ(·):Rn→RL是有N個隱層神經元并滿足φ(0)=0的線性無關的基向量,ε(x)是在線估計器的重構誤差,C是與x無關的常函數,在控制律設計時不需求出其值.選擇合適的φ(x)滿足. 例如,如果,那么0.選擇激活函數構造基向量使得 是漸近逼近的.根據Weierstrass高階逼近定理,只要V(x)足夠光滑這樣的基函數就是存在的.在線神經網絡的目標常值向量、重構誤差及重構誤差對x的偏導上界分別記為,. 把式(21)分別代入式(17)和式(18),可得: 根據式(14)以及g(x)B和?xε的上界,可得εHJB的上界. 把在線神經網絡對(21)的估計值表示為 由式(24)和式(25)可得哈密頓函數的估計值 考慮執行器故障的情況,控制律應滿足 式中,l=1,···,m,Γ1=diag{Γ11,Γ12,···,Γ1m}∈Rm×m>0和Γ2∈Rm×m>0均為正定增益對角矩陣,需要根據系統的實際情況進行設計和調節.χ和分別是矩陣主對角線上絕對值最小的元素和與之對應的導數. 定理1.對于存在執行器故障(2)的非線性系統(1),設計控制律(30),設計神經網絡權值更新律(27),自適應參數調整律(31)和(32),閉環跟蹤控制系統穩定,且跟蹤誤差和神經網絡估計誤差一致最終有界. 證明.見附錄A.□ 以文獻[30]中的飛翼飛行器作為控制對象,來驗證本文控制律的控制效果.該飛行器的縱向非線性運動方程為 其中,V是飛行速度;α是迎角;θ是俯仰角;q是俯仰角速率;輸入變量u1、u2表示兩個發動機的油門開度;輸入變量u3和u4分別為左右內升降舵偏角,u5和u6分別為左右外升降舵偏角.f1,f2,f4,G1,G2,G4表達式詳見文獻[30].取V、α、θ、q分別為系統狀態x1、x2、x3、x4,系統輸入u=[u1,u2,u3,u4,u5,u6]. ?f1,?f2,?f4分別為關于f1,f2,f4的不確定項,本文設定?f1=0.2f1,?f2=?0.2f2,?f4=?0.1f4. 系統輸出y=[x1,x3]T,參考信號分別為205+10sin(0.1t)和10sin(0.1t).給定系統的代價函數(9)中Q=[100,100],R=[100,1].系統和觀測狀態的初始狀態都設為x(0)=[200m/s,0,3?,0]T.神經網絡權值初始值全部設為0,這就意味著不需要給系統設置一個容許范圍內的初始控制輸入.選取代價函數在線估計神經網絡基函數為,自適應增益矩陣 Γ1=1000I6×6, Γ2=diag{0.001,0.001,0.1,0.1,0.1,0.1},在線神經網絡調整參數α1=0.1,α2=1.設飛行器在t=100s時,右側外升降舵u6發生卡死在u6=6?的故障;在t=200s時,左側外升降舵u5發生λ5=0.4的失效故障;在t=300s,左側內升降舵u3發生卡死在u3=?8?的故障,并且右側內升降舵u4發生λ4=0.6的失效故障.將本文方法與文獻[13]中所述的指定性能邊界的方法比較,在進行仿真時對比兩種方法的控制效果,仿真結果如圖1~6所示. 圖1 本文方法的y1和yr1Fig.1y1andyr1of the proposed method 圖2 文獻[13]方法的y1和yr1Fig.2y1andyr1of[13] 由圖1~圖4可知,在執行器出現卡死或失效故障后,兩種控制方法均可以實現對給定參考信號跟蹤,而本文方法具有更好的跟蹤性能.圖5與圖6為在兩種控制方法下系統跟蹤誤差的對比圖,可以看出在當前參數設置下,t=0s~100s系統無故障時前者對yr1的跟蹤效果比后者好,兩種方法對yr2的跟蹤效果差別不明顯.t=100s~400s故障發生后,前者跟蹤效果幾乎不受影響,而后者由于故障的原因則出現一定程度的跟蹤誤差增大.無論對于執行器卡死故障(t=100s~200s)、失效故障(t=200s~300s)、以及卡死和失效組合故障(t=300s~400s),相比可以看出前者具有更好的容錯性能. 圖3 本文方法的y2和yr2Fig.3y2andyr2of the proposed method 圖4 文獻[13]方法的y2和yr2Fig.4y2andyr2of[13] 圖5 本文和文獻[13]方法的y1跟蹤誤差e1,e11Fig.5 Tracking errorse1,e11ofy1by the proposed method and[13] 圖6 本文和文獻[13]方法的y2跟蹤誤差e2,e22Fig.6 Tracking errorse2,e22ofy2by the proposed method and[13] 圖7 系統狀態誤差估計2Fig.7Estimating error of system state2 圖8 不確定項估計神經網絡權值W2Fig.8 WeightsW2of uncertainty estimating neural network 本文針對一類具有不確定項以及執行器故障的MIMO仿射非線性系統的輸出跟蹤問題,考慮系統的執行器卡死、部分失效及其組合故障,提出了一種基于動態規劃的最優自適應補償控制方案.在構造系統狀態估計器估計系統不確定項的基礎上,設計了最優自適應補償跟蹤控制律.提出的控制方法能夠使閉環系統的所有狀態有界,并有效跟蹤參考信號.仿真結果表明了本文設計方法的有效性. 附錄A 定理1證明. 選取系統Lyapunov函數為 求導得 那么若不等式(A5)成立,則式(A4)小于0. 若下列不等式(A6)成立,則式(A4)小于0. 不等式(A5)和(A6)保證了當kek≥be,時,其中,be=max(be0,be1),bΘ=max(bΘ0,bΘ1)是正常數并可以通過選擇合適的參數α1和α2來減小它們的值. 因此,根據李雅普諾夫推論[20],系統輸出跟蹤誤差e和在線神經網絡估計誤差在兩種情況下都能保持一致最終有界.□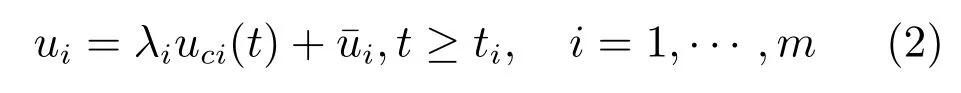
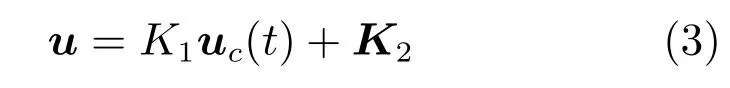
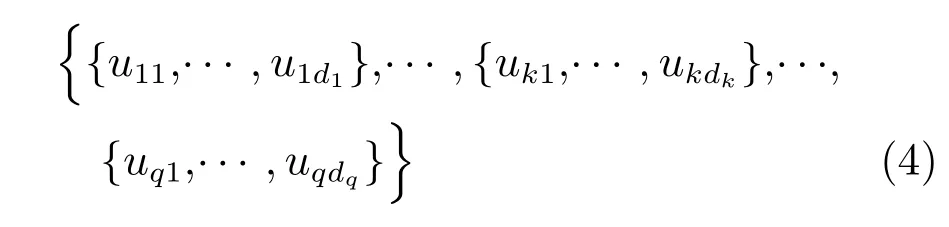
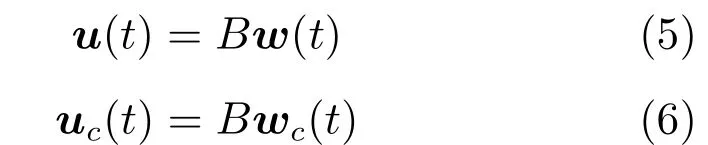
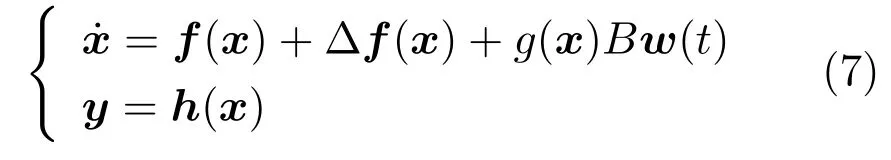

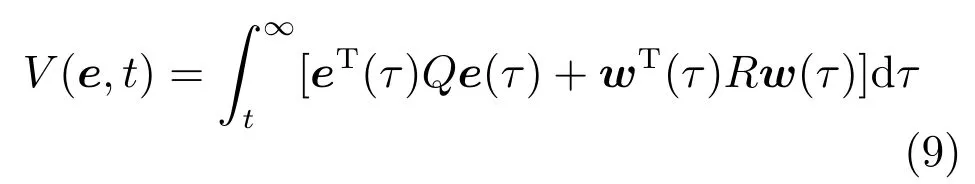
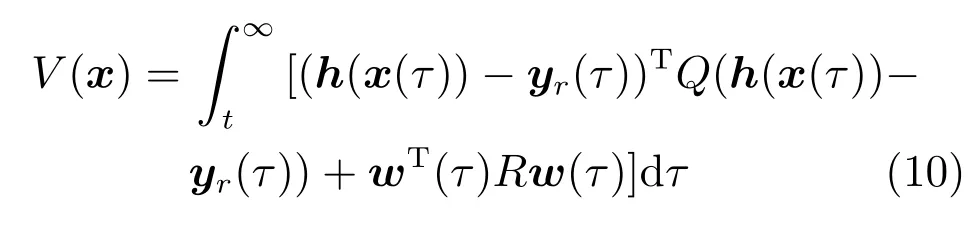
2 容錯控制律設計
2.1 不確定性估計器設計
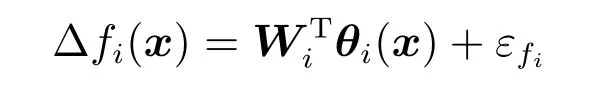
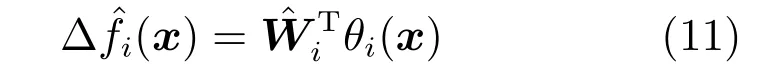
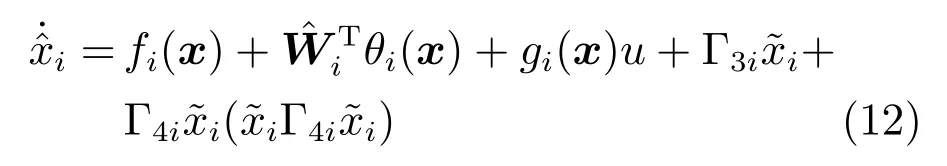
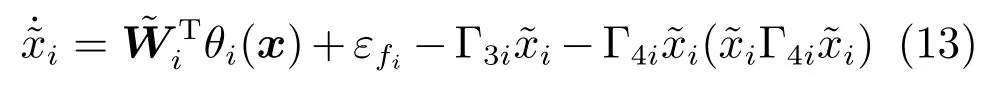
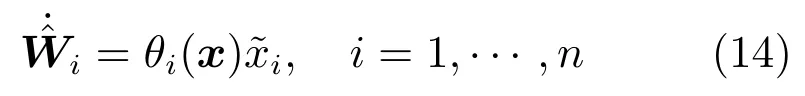
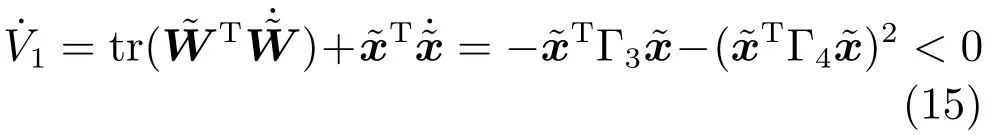
2.2 最優控制律設計
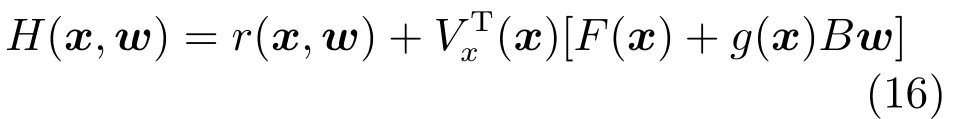
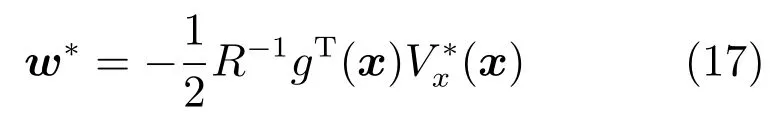
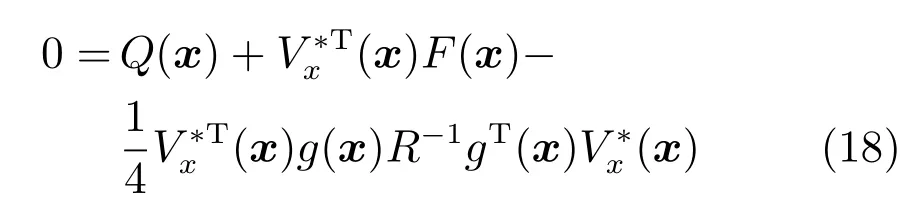
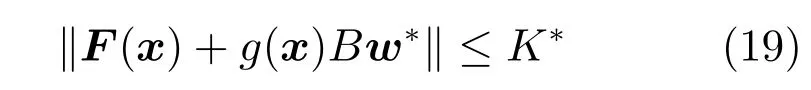
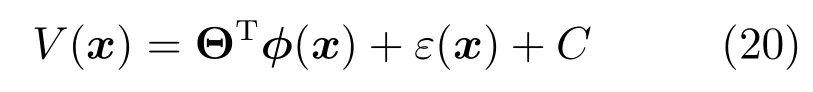
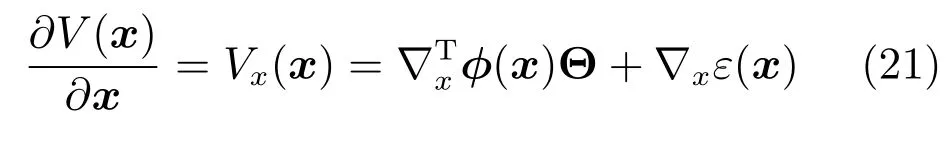
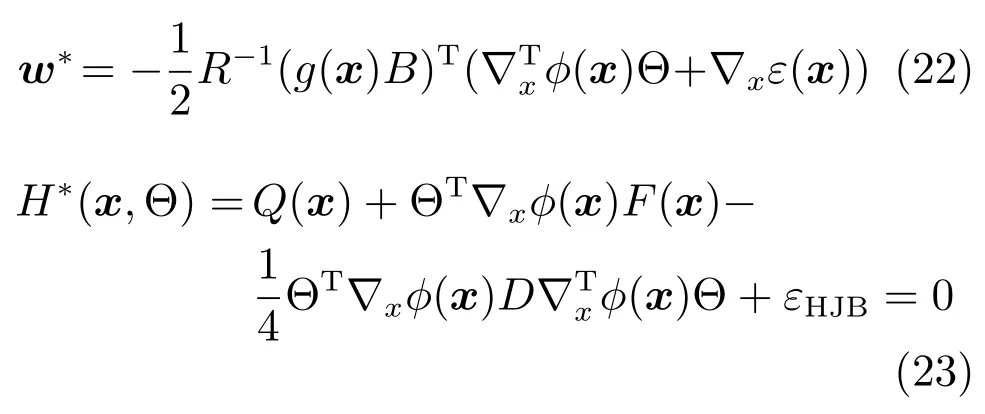
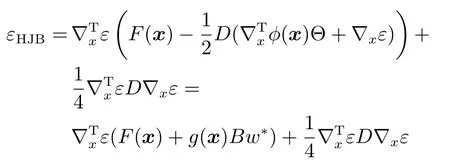
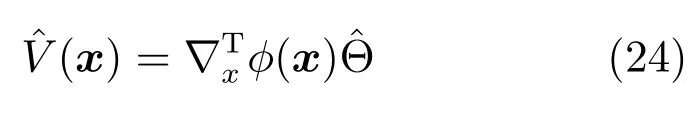
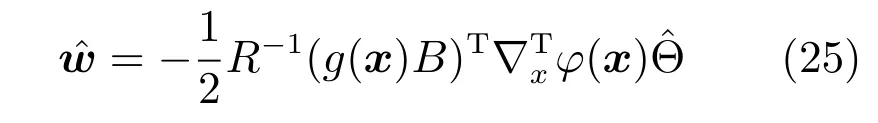
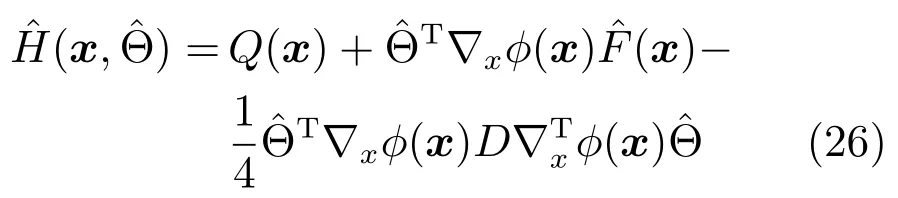
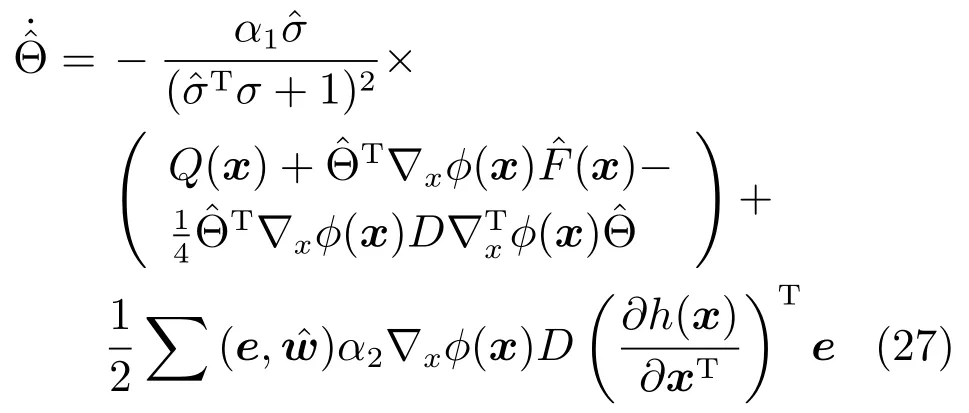

2.3 自適應補償控制律設計
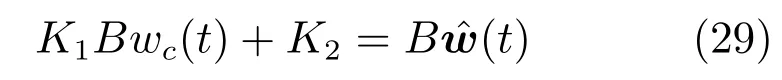
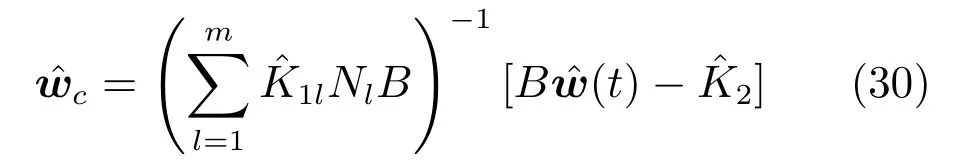
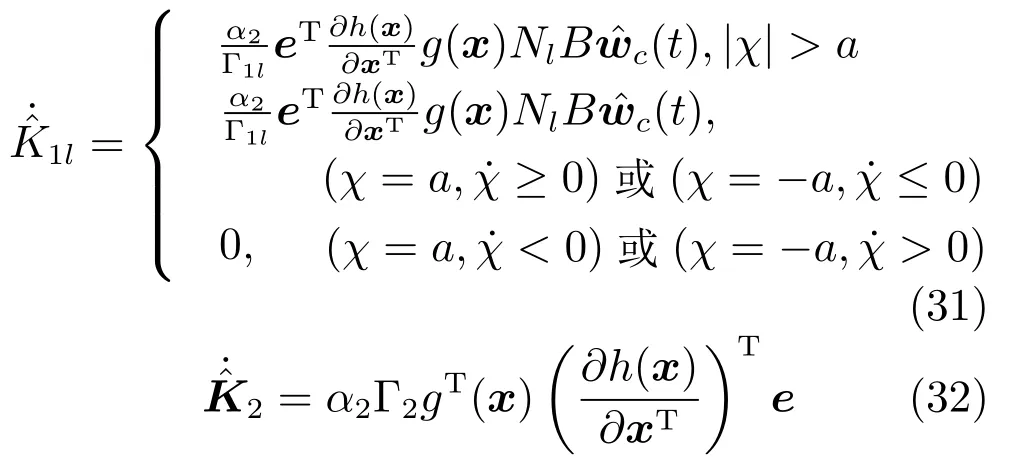
3 仿真算例
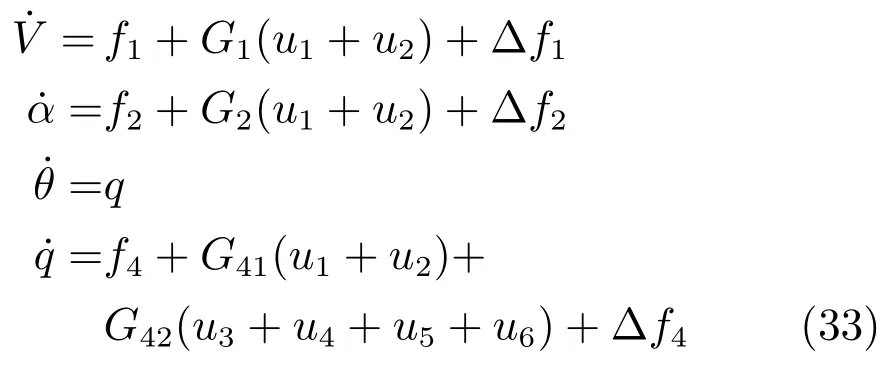
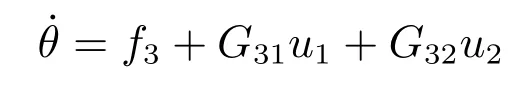

4 結束語