簡單流體系統的建模與仿真

孫 建，張 奇

(中海油能源發展股份有限公司采油服務分公司，天津 300451)

1 單個水槽系統的動態模型

考慮如圖1所示的單個水槽模型，其水槽底的液體流出的速度是槽內的液壓決定的。各部分的含義為:A—蓄水槽的表面區域;V—水槽的容積;Ae—水槽出口處的聯通部分;P1—槽底的液壓.液體的輸出壓強為Pa,輸出液體的速率作為系統的輸入.系統的狀態變量包括槽內液體的高度,其系統輸出為液體流出的速率We.根據系統的物質平衡,可得到:

圖1 單水槽系統示意圖

假設蓄水槽的四周壁是垂直的,槽內液體的質量是液體的密度誠意液體的體積,有

輸出液體的質量可以寫成輸出速率的函數

假設整個系統不存在能量或物質的滯留,并且忽略內部能量的變化,則根據能量守恒原理可以得到(5)：

綜合上面的方程得出

顯然該系統的狀態方程是一階非線性的,槽內液體質量的瞬時變化等于輸入的液體速率漸趨輸出的速率,槽內的液體質量和輸出液體的速率都視作t時刻液體高度的函數.

以上得出的方程顯然與顯示生活中的系統差別較大,可以逐步進行改進以得到更精確的模型.定義液體的阻力作用,它的作用與電路中電阻的作用類似:

與此類似,還可以定義該系統的電容效應,它反映了水槽存儲液體容量的變化.

將(7)和(8)代入式(6),得到

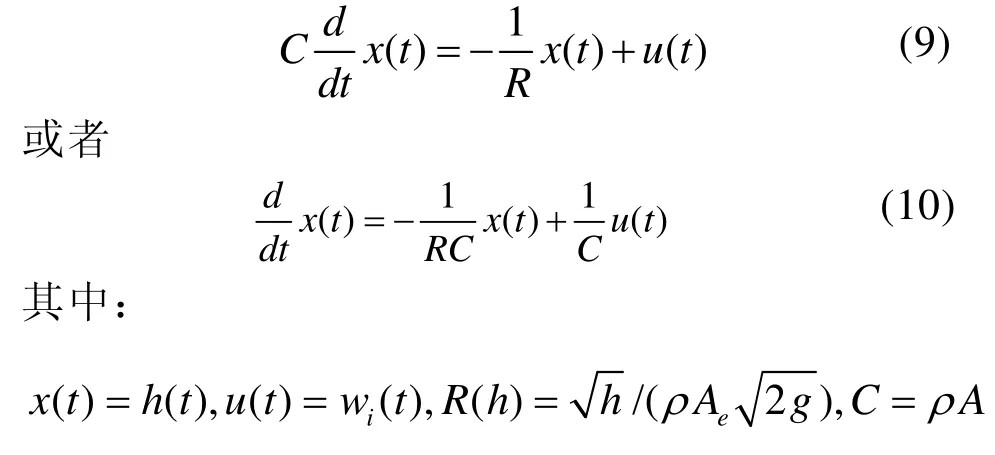
該非線性系統也可以線性化并寫成標準的狀態方程形式.定義系統的參考位置：

系統方程(1-6)可以寫成

式(15)即為系統的線性化模型[1]。為了比較非線性系統線性化前后的系統響應.定義系統參數:

系統參考位置的系統參數為：

依據上述參數可以對系統進行仿真，圖2顯示的分別是Wi分別改變10%和50%時非線性系統和線性化模型的階躍響應曲線。圖3、圖4給出了該系統線性化模型的頻域仿真結果[2]。

圖2 單水槽時域特性

2 雙槽水槽系統的模型建立

在實際應用中經常存在互相聯通的多個蓄水槽系統,這使得系統呈現出更高階動態系統的特性.下面以雙聯通的蓄水槽系統為對象,研究二階系統的動態行為。

圖3 系統線性化模型的BODE圖

圖4 其它頻域特性（Nyquist曲線和Nichols圖）

圖5 雙水槽系統示意圖

按照第1節對單個水槽的分析,可以確定1號和2號蓄水槽的液體輸出流量分別為[3]

從而得到兩個蓄水槽的平衡方程為：

將上面的結果寫成標準的狀態方程形式,并且將液體輸出流速作為系統輸出,則：

上述方程中的h1,h2 和 wi實際上是相對于參考位置的偏移量(即h1=δh1等)。為了創建系統的simulink方框圖,只要針對狀態方程中每個SISO子系統繪制它的框圖,如下所示,然后將它們連接起來即可。

圖6 各個子系統的框圖

仿真框圖如下所示：

圖7 整個系統的框圖結構

整個系統的傳遞函數可以通過矩陣運算或相關模塊框圖計算得到：

上式代入式(19),得到：

整理后得到整個系統的傳遞函數為：

圖8和圖9為該系統的脈沖和階躍響應的部分仿真結果,程序對雙水槽系統的 兩種不通情況進行了仿真.一種是針對系統參考位置的動態行為進行了仿真.一種是將1號水槽的容積增加了1倍,這將導致系統時間常數的增加。

圖8 雙水槽系統的時域響應

3 結束語

在以上兩個系統的建模與仿真中，分別建立了非線性和線性模型，仿真時對系統參數做了修改，以求得到反映系統特性的信息，在仿真結果中比較明顯反映出了這些差別，可見對于此類基礎的模型建立與仿真對于加深對系統的認識具有很大意義。

圖9 雙水槽系統的Bode圖

參考文獻：

[1] 鄭阿奇.MATLAB實用教程[M].北京：電子工業出版社,2011

[2] 趙文峰.MATLAB控制系統設計與仿真[M].西安：西安電子科技大學出版社,2002

[3] 金以慧.過程控制[M].北京：清華大學出版社,2005.