一類具有新參數的最優低碰撞區跳頻序列集

呂 中，張永輝

（中建西部建設西南有限公司，四川 成都 610040）

0 引 言

跳頻多址擴頻系統由于它的抗干擾性、安全性、多址性，被廣泛應用于藍牙、軍事電臺通信、移動通信、現代雷達和聲納回聲定位系統等[1]。在這些系統中，跳頻擴頻通信技術[2]通過載波率持續不同的跳變，最終保障頻譜展寬。利用偽隨機碼實現對信號載波頻率的操作，在規劃范圍中順利進行運作，實現合成器頻率始終保持著變化。由于偽隨機碼可以使接收器得到良好的控制，使得接收端與發射端在變化規律上具有同步性。此外，偽隨機序列在跳頻系統中不主要用于信道選擇，并不會以直接的形式進行傳輸?；谒墓ぷ髟?，偽隨機碼有了一個全新的代名詞，即跳頻序列，又名調跳頻碼。通常情況下，在碼分多址環境中，總是希望保持發射機之間的相互干擾在盡可能低的水平[3-4]。當兩個或多個發射機同時在同一頻率上傳輸時，易發生相互干擾，而相互干擾的程度和跳頻序列的漢明相關性緊密相連。從這一點可以看出，對于跳頻技術的研究，首要是能夠設計出具備漢明特性的跳頻序列。

2003年，Ye等人[5-6]首次提出LHZ/NHZ跳頻序列的概念。低碰撞區跳頻序列是一種具有特殊性質的跳頻序列，系統對多址干擾抗性的能力，很大程度上取決于臨近零時延序列的漢明性能[7-9]。

本文主要研究低碰撞區跳頻序列的設計，剩余部分組織如下：第2部分，給出關于跳頻序列的一些預備知識；第3部分，介紹交織序列理論；第4部分，構造一類具有新參數的最優低碰撞區跳頻序列集；第5部分是對本文的總結。

1 預備知識

首先給出跳頻序列漢明相關函數的定義。將F={ f0,f1,…, fq-1}作為頻隙集，其大小設定成q，N的跳頻序列組成的集合根據F上M個長度S來代表。

定義1：設頻隙集F={ f0, f1,…, fq-1}，x={x0, x1,…, xN-1}，y={y0, y1,…, yN-1}，（xi, yi∈ F,i=0,1,…,N-1）為頻隙集F上兩個長度為N的跳頻序列，x和y在相對時延τ的周期漢明互相關函數為：

式中，i+τ按模 N 運算。當x=y時，H(x y·,τ)稱為周期漢明自相關函數；當x≠y時，H(x y·,τ)被叫做周期漢明互相關函數。

跳頻序列集S為已知的前提下，序列集的三個最大周期的漢明自相關Ha(S)、Hc(S)以及Hm(S)的定義如下：

Ha(S)=max{H(x x·,τ)|x ∈ S,0 ＜ τ＜ N}

Hc(S)=max{H(x y·,τ)|x,y∈ S, x≠ y,0 ≤ τ＜ N}

Hm(S)=max{Ha(S),Hc(S)}

為了簡化和方便，令Ha=Ha(S)，Hc=Hc(S)，Hm=Hm(S)。

跳頻序列集的最大周期漢明相關值的下界于2004年被建立[10]。

引理1（Peng-Fan界）：令F是一個大小為q的頻隙集，S為F上M個長度為N的跳頻序列構成的集合，有：

對于任意跳頻序列集S，令整數Ha≥0，Hc≥0，F作為頻隙集，其大小設定成q，S是F上M個長度為N的低碰撞區跳頻序列構成的集合。如此，LH、LAH、LCH的定義如下：

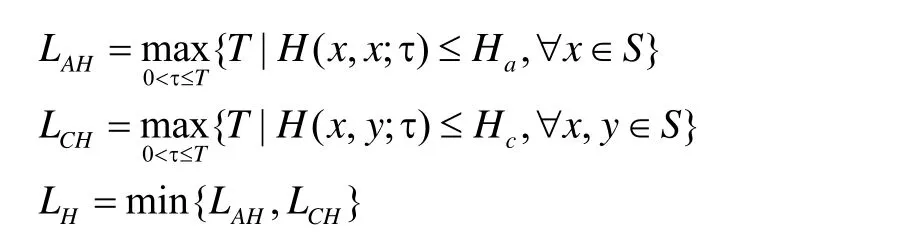
如果Ha=Hc=0時，S的低碰撞區稱為S的無碰撞區NH。S作為一個具備LH≥0或NH≥0的跳頻序列集，被叫做無碰撞區跳頻序列集，代表涉及周期漢明相關的低碰撞區跳頻序列集。以Peng為代表[11]的研究學者，于2004年對LHZ跳頻序列集的周期漢明相關理論界進行了推導。

引理2（Peng-Fan-Lee界）：令F是一個大小為q的頻隙集，F上M個長度為N的跳頻序列構成的集合代表S，序列集S關于周期漢明相關函數的低碰撞區代表LH。所有整數Z，0≤Z≤LH，有：

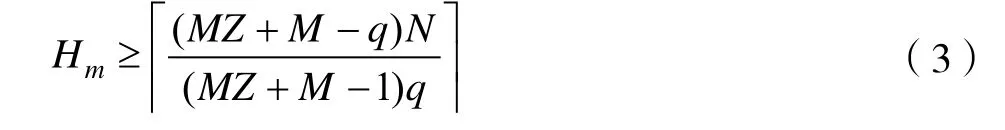
2 交織序列理論

交織序列理論在1995年由Gong首先提出[12]，本節將對交織理論進行簡單介紹。

設a=(a0,a1,…,aN-1)是一個F上頻隙集大小為q、長度為N、最大漢明自相關值為Ha的跳頻序列。設e=(e0,e1,…,eT-1)是ZN上的移位序列，其長度為T。則由序列a與移位序列e能夠組成N×T的矩陣U：

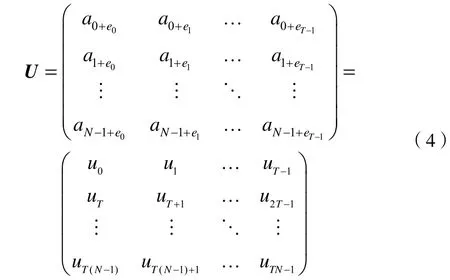
這里，按模N運算下標。按行間順序讀出矩陣U中的元素，能夠獲得周期為NT的序列u=(u0,u1,…,uNT-1)。此時a可叫做基序列，u又叫做交織序列，而e則叫做移位序列。序列u的矩陣表示為矩陣U。優化后將u=I(Le0(a),Le1(a),…,LeT-I(a))表示為交織序列u，其中I表示交織操作。

令g=(g0,g1,…,gT-1)為ZN上長度為T的移位序列，可生成交織序列：

v=I(Lg0(a),Lg1(a),…,LgT-I(a)) （5）

對于時延 τ=Tτ1+τ2(0 ≤ τ1＜ N,0 ≤ τ2＜ T)，序列 v的移位Lτ(v)的矩陣表示為：

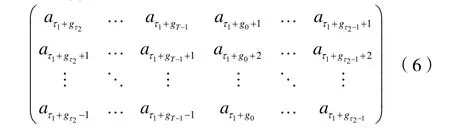
顯然，Lτ(v)是另外一個交織序列，可以表示為：

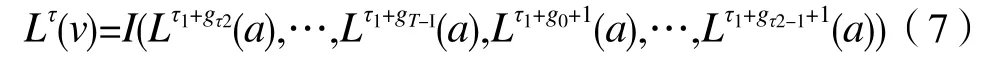
交織序v與u處于時延τ時的漢明相關函數，根據式（4）和式（6）中列序列內積的和的計算可以得出：

3 最優低碰撞區跳頻序列集的構造

將基于上述交織技術構造新的最優LHZ FHS集。設F={ f0, f1,…, fq-1}是一個大小為q的頻隙集，其序列集構造如下。

構造1：低碰撞區跳頻序列集的一般化構造

步驟1：選取F上頻隙集大小為q的l個長度為N、最大漢明相關值為Hm的跳頻序列構成的集合A=(N,q,l,Hm)：

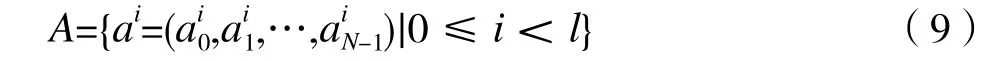
步驟2：對于給定的T，令M為正整數，滿足gcd(N,T)=1，生成移位序列集H={E,G}，有：

步驟3：構造低碰撞區跳頻序列集S={SA,SB}。

①由基序列集A={ai=(ai0,ai1,…,)|0≤i＜l}和移位序列集E進行交織，得到LHZ FHS集SA={|0≤x＜Ml}，其中x=iM+j(0≤i＜l,0≤j＜M)。對于任意的0≤x＜Ml，有：

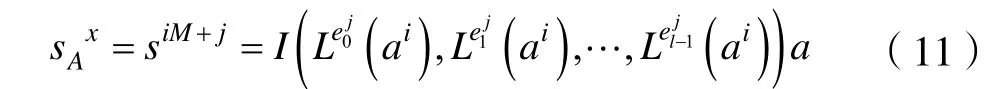
②通過序列集A得到基序列B={a0,a1,…,al-1},由該基序列B和移位序列集G進行交織，得到LHZ FHS集SB=|0≤y＜M(T-2l+1)}，其中0≤k＜M(T-2l+1)且k∈Z，對于任意的0≤k＜M(T-2l+1)，有：

下面給出最優低碰撞區跳頻序列集的具體構造。

構造2：最優低碰撞區跳頻序列集的構造

步驟1：選擇一個在F={ f0, f1,…, fq-1}上的最優跳頻序列集A=(N,q,l,Hm)：

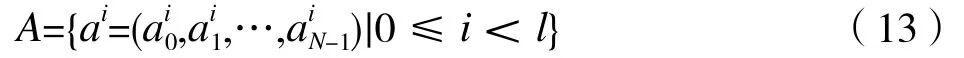
步驟2：令M、w和T為三個正整數，且滿足：

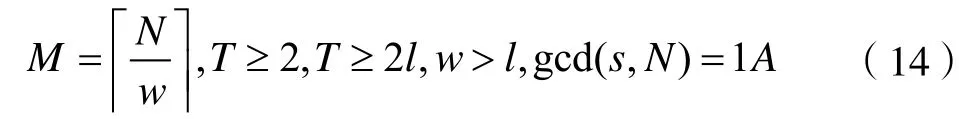
構造移位序列集H={E,G}，有：

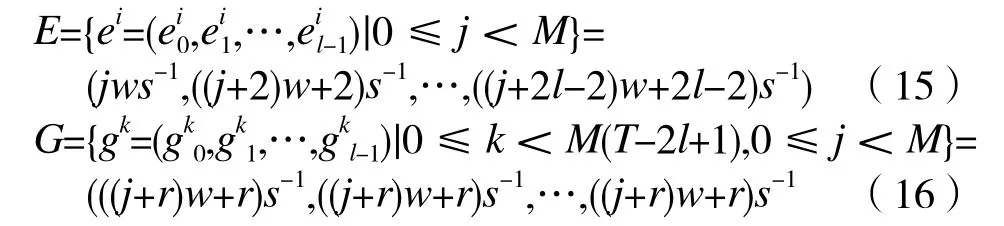
其中2l-2＜r＜T且r∈Z。

步驟3：構造最優低碰撞區跳頻序列集S={SA,SB}。①由基序列集A和移位序列集E進行交織，得到LHZ FHS集SA={|0≤ x＜ Ml}：

其中 x=iM+j(0≤i＜ l,0≤ j＜ M)。

②由基序列B和移位序列集G進行交織，得到LHZ FHS集SB={|0≤ y＜ M(T-2l+1)}：

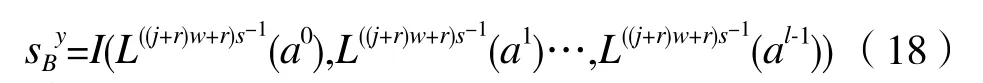
其中0≤j＜M，2l≤T，2l-2＜r＜T且r∈Z。

定理1：在構造2中，如果參數滿足：

（1）T=λw+1,λ≥ 0,T≥ 2l,w ＞ l

則生成的跳頻序列集S是一個最優的(lN,q(T-l+1)M,l-1;lHm)低碰撞區跳頻序列集。

證明：首先證明跳頻序列的低碰撞區。

與參考文獻[9]中定理2的證明類似，可以得出，當T=λw+1,λ≥0時，由基序列集A與移位序列集E進行交織構造的低碰撞區跳頻序列集SA的低碰撞區=w-1。

與參考文獻[9]中定理1的證明類似，可以得出由基序列B與移位序列集G進行交織構造的低碰撞區跳頻序列集SB的低碰撞區LBH=wl-1。

由此容易得出：低碰撞區跳頻序列集SA和SB之間的低碰撞區LABH=l-1。

綜上所述，可以得出上述低碰撞區跳頻序列集的低碰撞區為：

構造2中的跳頻序列集參數如下：序列長度為lN，序列個數為(T-l+1)M，頻隙集F的大小為q。令Z=LH，根據Peng-Fan-Lee界[11]，跳頻序列集S的最大漢明相關應為：

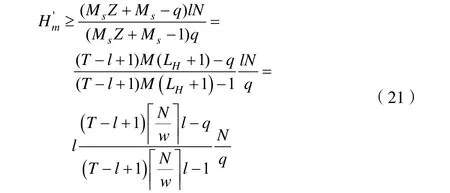
由于最優跳頻序列集A滿足Peng-Fan界[10]，于是可以得出：

可以看出，在Peng-Fan-Lee界的要求內容上，低碰撞區跳頻序列集S的最大漢明相關均可以滿足。因此，最優的低碰撞區跳頻序列集完全可以以序列集S作為定義。證明結束。

例1：

步驟1：選擇一個最優的（16，7，3，2）跳頻序列集A={a0,a1,a2}，其中：

步驟2：選擇s=1，T=8，w=8，則有M=N/w=2。

生成移位序列集H={E,G}的矩陣表示為：

H=[E G] （27）

步驟3：根據構造2的方法構造低碰撞區跳頻序列集：

跳頻序列集S的最大漢明自相關和最大漢明互相關，通過計算完全可以得出結果，見圖1。

圖1 例1中序列集S的最大漢明相關

通過簡單的證明可以得出，任意兩個跳頻序列的漢明互相值關不一定總是相同，但對于跳頻序列集S來說，即取其最大值。同理，漢明自相關值不一定總是相同，但對于跳頻序列集S來說就取其最大值。當τ＜3時序列集的最大漢明相關Hm=6。因此，S是最優的（48，7，12，2；6）低碰撞區跳頻序列集。

4 結 論

基于交織技術構造了一類具有新參數的最優LHZ FHS集。通過選擇一些已知的最優FHS集，然后在滿足特定條件下可以構造出最優的低碰撞區FHS。通過使用不同的移位序列，可以構造出參數設置更靈活的低碰撞區FHS集。該FHS集可以應用到準同步的跳時/跳頻碼分多址系統中，用于消除多址干擾。

[1] 梅文華，楊義先.跳頻通信編碼地址理論[M].北京：國防工業出版社，1996.

[2] 梅文華，王淑波，邱永紅.跳頻通信[M].北京：國防工業出版社，2005.

[3] Wu T，Chao C，Chen K.Capacity of Synchronous Coded DSSFH and FFH Spread-spectrum Multiple-access for Wireless Local Communications[J].IEEE Trans. on Commun.，1997（45）：200-212.

[4] Torrieri D J.Mobile Frequency-hopping CDMA Systems[J].IEEE Trans.Commun.，2000，48（8）：1318-1327.

[5] Ye W X，Fan P Z.Two Class of Frequency-hopping Sequences with No-hit Zone[C].Proceedings of the Seventh International Symposium on Communications Theory and Applications（ISCTA’2003），2003：304-306.

[6] Wang X N，Fan P Z.A Class of Frequency Hopping Aequences with no Hit Zone[C].Proceedings of the Fourth International Conference on Parallel and Distributed Computing，pplications and Technologies（PDCAT’2003），2003：27-29.

[7] WANG Chang-yuan，PENG Dai-yuan，Limengnan Z.New Constructions of Optimal Frequency-Hopping Sequence Sets with Low-Hit-Zone[J].International Journal of Foundations of Computer Science，2016，27（1）：53-66.

[8] Ma W P，Sun S H.New Designs of Frequency Hopping Sequences with Low Hit Zone[J].Designs，Codes and Cryptography，2010：145-153.

[9] Niu X H，Peng D Y，Zhou Z C.New Classes of Optimal Low Hit Zone Frequency Hopping Sequence with New Parameters by Interleaving Techniques[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Science，2012，E95-A (11):（11）：1835-1842.

[10] Peng D Y，Fan P Z.Lower Bounds on the Hamming Auto and Cross Correlations of Frequency-hopping Sequences[J].IEEE Trans. Inform.Theory.，2004，50（9）：2149-2154.

[11] Peng D Y，Fan P Z，Lee M H.Lower Bounds on the Periodic Hamming Correlations of Frequency Hopping Sequences with Low Hit Zone[J].Science in China，2006，49（2）：208-218.

[12] Gong G.Theory and Applications of q-ary Interleaved Sequences[J].IEEE Trans. Inform. Theory.，1995，41（2）：400-411.